基于改進卡爾曼濾波的電力計量計費數據狀態評價研究
摘要:針對電力計量計費數據通信方式多、數據量大的問題,提出了以改進無跡卡爾曼濾波的電力計量計費數據狀態評價方法。分析了無跡卡爾曼濾波無跡變換原理,構建了動態傳輸策略。為進一步提高無跡卡爾曼濾波評價結果精度,構建了自適應因子對算法進行修正,降低了算法運行過程中的影響因素。最后為驗證提出算法的有效性和可行性,以IEEE-33節點電力系統為例進行了仿真分析。分析結果表明,改進卡爾曼濾波的電力計量計費數據狀態評價可以滿足電力計量計費數據狀態評價精度和實時性要求。
關鍵詞:卡爾曼濾波電力計量計費數據動態傳輸自適應因子無跡變換
中圖分類號:TM7
StateEvaluationofPowerMeteringandBillingDataBasedonImprovedKalmanFilteringUnderDynamicTransmission
ZHANGXiaodongWUXiang
StateGridNingxiaMarketingServiceCenter(StateGridNingxiaMetrologyCenter),
Yinchuan,NingxiaHuiAutonomousRegion,750011China
Abstract:Regardingtheproblemofmultiplecommunicationmodesandlargedatavolumeofpowermeteringandbillingdata,amethodforevaluatingthestatusofelectricitymeteringandbillingdatawithimprovedunscentedKalmanfilteringisproposed.TheprincipleofunscentedKalmanfilteringisanalyzed,andthedynamictransmissionstrategyisconstructed.InordertofurtherimprovetheaccuracyoftheunscentedKalmanfilteringevaluationresults,anadaptivefactorisconstructedtomodifythealgorithmandreducetheinfluencingfactorsintheoperationofthealgorithm.Finally,toverifytheeffectivenessandfeasibilityoftheproposedalgorithm,simulationanalysisisconductedontheIEEE-33nodepowersystem.TheanalysisresultsshowsthattheimprovedKalmanfilteringforpowermeteringandbillingdatastateevaluationcanmeettheaccuracyandreal-timerequirementsofpowermeteringandbillingdatastateevaluation.
KeyWords:Kalmanfiltering;Electricitymeteringandbillingdata;Dynamictransmission;Adaptivefactor;Unscentedtransformation
近年來主要通過編譯各種電網片段的電能平衡分析電表的實際數據,主要是向內和向外電能流量的簡單總和。但是,用于計算和分析所有網格元素的電流流量和損失的精確計算數學模型相當有限。從實現技術上來講,早期的關口電能量自動抄表經歷了兩個發展階段。第一,20世紀70—80年代,自動抄表是安全監視與數據采集系統SCADA的一個子功能,稱作遙脈、遙表或脈沖累加量。由于受當時電源系統和非易失性存儲器技術制約,電量數據的采集精度、可靠性、完整性均存在嚴重問題,實用性差。第二,從20世紀90年代至今,西方計量領域的知名制造商研發了獨立于SCADA系統的專門的自動抄表系統TMR。經過多年的發展,電力計量系統的實現技術逐步完善,實用化水平已基本滿足需要。
本文針對無跡卡爾曼濾波(UnscentedKalmanFilter,UKF)預測結果誤差較大、易受不良數據影響的問題,構建了自適應因子,提出了改進無跡卡爾曼濾波(AdaptiveUnscentedKalmanFilter,AUKF)評價和預測電力計量計費數據狀態。
1無跡卡爾曼濾波基本原理
UKF是一種利用無跡變化對隨機變量進行評估分析的方法,其核心內容是無跡變換[1]。
1.1無跡變換
為保證算法評估準確性和精度,利用對稱比例對采樣法進行修正。在n維電力系統中,k-1時刻2n+1個sigma點和權值計算公式如下。
式(1)、式(2)中:為k-1時刻電力系統狀態評估值;為電力系統尺度因子,主要用于降低評估誤差;α為采樣點分布狀態,其取值范圍[10-4,1];k為自由參數;β為權系數,其取值為2;為電力系統狀態量權值;為方差權值[2]。
1.2動態傳輸策略
根據狀態描述發構建電力計量計費數據狀態方程和測量方程數學模型:
式(3)中:xk為電力系統狀態變量;yk為電力系統測量向量;k為時刻;q為數學模型誤差;r為測量誤差。
動態傳輸模型包含了濾波步以及預測步兩個環節,其中,預測步又可以進一步細分為觀測預測與狀態預測兩部分。在獲得無跡變換所產生的sigma點以及相應的權重之后,通過運用平滑算法對電力計量計費數據的狀態進行準確預測。然后,將預測參數替換至測量函數當中以獲取觀測預測值[3]。而濾波步則主要在計算完柯爾曼濾波后,適當地調整觀測值及測量值,進而迭代更新狀態變量。具體實現流程如下所述:
1.2.1預測步
(1)狀態預測。
式(4)、式(5)、式(6)中:為sigma采樣點;為電力計量計費數據狀態預測值;為狀態量預測誤差矩陣。
利用平滑法獲取電力計量計費數據狀態轉移函數f:
式(7)中:為k時刻預測k+1時刻電力計量計費數據狀態量;為k時刻電力計量計費狀態評估值;和為平滑值,取值范圍0~1[4]。
(2)測量預測。
電力計量計費數據測量預測函數如下:
式(8)、式(9)中:為sigma采樣點;為電力計量計費數據狀態測量值。
1.2.2濾波步
式(10)至式(14)中:yk為電力系統實時測量值;Sk為電力計量計費數據預測方差矩陣;Ck為量測量和狀態量交叉方差矩陣;Kk為卡爾曼濾波增益矩陣。
從UKF濾波步驟和預測步驟的流程中來看,該算法中的sigma采樣方法是通過核算實現,不需要復雜的雅可比矩陣運算。然而值得注意的是,UKF基于歷史數據預測計費數據狀態時,可能會因預測結果受到很大程度的誤差影響,從而使得濾波效果降低,同時可能會引發濾波出現發散的問題[5]。
2改進無跡卡爾曼濾波
根據以上分析可知,增益矩陣Kk是影響電力計量計費數據狀態評價結果精度的主要因素,其中預測方差矩陣Sk和交叉方差矩陣Ck對于增益矩陣Kk影響較大。為進一步提高電計量計費數據評價結果準確性,構建自適應因子對以上方差矩陣進行修正。
定義數據向量為,然后判斷測量遠側誤差矩陣和信數據向量矩陣無跡的大小,并構建自適應因子:
在電力系統穩定運行狀態之下,所有數據向量的各個數據元素均處于誤差允許范圍之內,且數據矩陣的無跡值必須大于或等于所測得的預測誤差方差矩陣的無跡,在此條件下,自適應因子通常取數值1。如果數據向量中元素變大,致使數據矩陣無跡>測量預測誤差方差矩陣無跡,表明電力系統有負荷突變情況,此時電力計量計費數據狀態評價結果誤差加大,需要利用自適應因子對預測方差進行修正。
利用自適應因子對測量預測方差矩陣修正過程如下所示:
利用自適應因子對測量交叉方差矩陣和狀態量方差矩陣修正過程如下所示:
根據以上分析可知,在電力系統穩定運行情況下,改進UKF算法在電力計量與計費數據的評估所需時間并未有所延長;當電力系統發生異常狀況時,自適應參數可對誤差方差矩陣進行相應調整,并降低異常數據對評價結果的影響。
3算例分析
針對IEEE-33節點電力系統展開深入研究,驗證所提出的評價方法的有效性。如圖2所示的電網拓撲結構,在每一個節點上都安裝了具備高度智能化功能的電能計量設備。
采用動態傳輸策略的技術手段操控智能電表的運作模式,在這個過程中引入參數衡量數據從測量終端向用戶用電采集平臺傳輸的速率。通過調整傳輸函數中的傳輸閾值,控制數據的傳輸速度。在整個模擬過程中共進行50次采樣。同時,為模擬真實環境下可能出現的負荷波動情況,在每個節點的實際負荷基礎之上,額外增加了5%的隨機擾動。
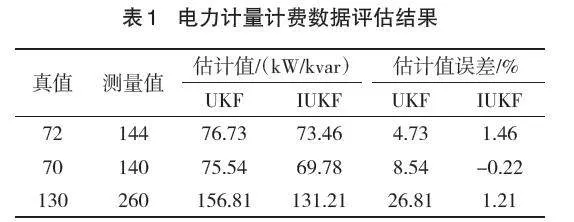
在電力系統存在不良數據的情況下,測量誤差結果大于±3σ的數據為不良數據[9]。表1為UKF和AUKF兩種算法電力計量計費數據評估結果。
從表1種可以看出,在電力系統存在壞數據情況下,改進后的AUKF算法獲取的評價結果更加準確,并且相對誤差較小,電力計量計費數據狀態評價精度更高。
在仿真采樣次數為50次時,AUKF算法計算時間為11.23s,單次計算時間為0.346s。目前電網SCADA系統數據采樣時間為2~5s,由此可見,本文提出算法不僅評價精度滿足要求,而且預測時間較短,可以滿足計量數據評估要求。
4結論
綜上所述,本文提出了基于無跡卡爾曼濾波的電力計量計費數據評估方法,通過測量預測誤差矩陣與數據矩陣構建自適應因子,解決了電力系統不良數據較多時UKF算法評價結果不準確的問題。通過對電力系統進行算法仿真和分析得到,本文提出電力計量計費數據狀態評價方法,可以滿足多種復雜運算情況下,電力計量計費數據狀態評價要求,并且評價結果精度較高。
參考文獻
[1]唐軍,王子夢,羅瑞智.基于乘性擴展卡爾曼濾波的水下機器人姿態估計[J].傳感器與微系統,2022,41(11):126-129.
[2]劉思幸,柴巖,柳天虹,等.基于卡爾曼濾波PID控制的精量排種器優化設計與試驗[J].中國農機化學報,2022,43(11):1-8,97.
[3]張彥澤,于斌超,馬大智,等.自適應擴展卡爾曼濾波機械臂末端定位[J].組合機床與自動化加工技術,2022(10):150-153,158.
[4]佘凱,趙振華,田江波.基于卡爾曼濾波算法的無人機避障路線智能生成方法[J].微型電腦應用,2022,38(10):58-60.
[5]劉玨,李飛成,張寧春,等.醫用耗材使用量的卡爾曼濾波預測模型構建與應用研究[J].中國醫學裝備,2022,19(10):138-142.

