區塊鏈上的零知識證明技術及其典型算法、工具綜述

摘要：在數據安全和隱私保護日益重要的背景下，零知識證明（Zero-Knowledge Proofs， ZKPs）為保護隱私提供了強有力的工具，成為最具應用潛力的核心技術之一。本文綜合探討了零知識證明技術及其在區塊鏈中的應用。首先，詳細介紹了零知識證明的相關概念以及三種典型的技術，對ZK-Snarks進行了深入探討，并討論了ZK-Stark和Bulletproofs等其他證明機制，深入對比分析了各自的設計、技術特點、性能和應用場景的差異。在此基礎上，重點介紹了ZKPs在區塊鏈環境下的應用，并分析整理了編寫零知識證明的相關工具，這些工具在提升具體應用的性能方面尤為重要。最后，指出了一些潛在的問題和未來的研究方向。

關鍵詞：零知識證明；隱私保護；區塊鏈應用

1 "引言

區塊鏈[1-2]通常被認為是一種公共的，分散的和分布式的賬本。在區塊鏈的環境下，所有的歷史交易數據都被記錄和存儲。通常，交易數據包括交易的實現細節，如交易金額、賬戶地址、賬戶余額等，屬于個人隱私。由于區塊鏈的開放性和透明性，任何人都可以訪問存檔的交易數據，當用戶數據請求存儲至區塊鏈以及數據被系統驗證時，這些數據信息會在一定程度上泄露給運行系統或其他用戶，降低鏈上數據的安全保密性，帶來嚴峻的安全和隱私挑戰[3]。隨著2008年中本聰設計Bitcoin開始，區塊鏈技術逐漸受到工業界與學術界的關注。區塊鏈技術的發展歷程涉及了多種隱私保護技術，包括同態加密[4]，環簽名[5]，安全多方計算[6]。同態加密允許對加密數據執行計算，而無需解密，從而在保持賬戶余額和交易金額私密性的同時，支持其可用性。然而，同態加密在確保賬戶地址隱私方面仍存在局限性。同態加密操作通常比非加密操作要復雜得多，這導致處理速度較慢，尤其是在需要大量計算的應用場景中，這種低效率可能成為一個重大障礙。與此相反，環簽名技術允許隱藏簽名者的身份，為賬戶地址的保密提供了一種有效手段，但它并不涉及對余額或交易量的保護。安全多方計算則通過分散的計算任務來確保各方數據的隱私，每個參與者僅知曉自己的輸入，無法獲得其他參與者的詳細數據，這在一定程度上保證了交易的安全性，但無法確保賬戶地址的匿名性[7]。

零知識證明（ZKP）是由Goldwasser等人[8]首先提出的，在密碼學領域有著重要的應用。它能夠保證證明者在不提供任何有用的相關信息的情況下，使驗證者相信一個語句是真實的。零知識證明允許證明者產生一個簡短的證明π，可以說服任何驗證者相信證明者的公共輸入x和秘密輸入w上的公共函數f的結果是y = f（x，w）。w通常被稱為見證輸入或輔助輸入。零知識證明保證了如果證明者在計算結果時作弊，驗證者以壓倒性的概率拒絕，而證明過程不會透露關于秘密w的額外信息，包括證明者的數據、證明者的身份和驗證者的身份等。在區塊鏈應用中，驗證者可以使用ZKP來驗證證明者在區塊鏈環境中是否有足夠的交易量，而不會泄露任何私有交易數據。

不同的零知識證明算法在初始設置，證明方式和驗證方式等方面具有不同的特性，依據使用的方法和問題需求的不同，這使得它們適用于不同的場景及領域。本文中主要討論三種在區塊鏈上應用最廣的零知識證明算法：ZK-SNARK[8]，ZK-STARK[9]及Bulletproof[11]。相比而言，ZK-SNARK提供了一個相對較短的證明長度，而zk-STARK [9]比其他類型的零知識證明具有更快的驗證和證明速度，且不需要可信設置，這兩個特性意味著zkSTARKs在投票系統和在線身份識別系統等場景中可能具有巨大的潛力[10]，而Bulletproof是一種新型的非交互式零知識證明，同樣不需要可信的設置過程，適用于范圍證明。

本文的組織結構如下：文章首先引入了零知識證明的相關定義，然后討論了不同類型的零知識證明以及它們的技術特點和應用場景。特別地，本文對ZK-Snarks的發展歷程進行了深入研究，分析了如何通過PCP（Probabilistically Checkable Proofs）和QAP（Quadratic Arithmetic Programs）進行ZK-Snarks的構造，然后，重點介紹了ZKP在區塊鏈環境下的應用，并分析整理了編寫零知識證明的相關工具。最后，本文指出了零知識證明領域一些潛在的問題和未來的研究方向。

2 "零知識證明相關基礎介紹

本章將介紹零知識證明的相關概念及典型技術。

2.1 "零知識證明相關概念

2.1.1 "NP語言：如果對于語言L，存在一個多項式時間圖靈機RL和一個多項式p（n）使得：x∈L，當且僅當存在y，|y| ≤ p（|x|）， RL（x，y） =1。

2.1.2 "交互證明（Interactive proof）[12]：一對交互式圖靈機（P，V），其中P表示一個在時間多項式內運行的概率性“誠實”證明者算法，P*表示惡意的證明者算法， V表示一個在多項式時間內運行且確定性的先驗算法，（P，V）被稱為語言L的一個交互式證明系統，如果以下條件成立：

完備性：Pr[（P，V）（x）=1]＞1-negl（n）

可靠性：Pr[（P*，V）（x）=1]≤1-negl（n）

其中：Pr表示概率，negl（n）表示一個在輸入大小 n 的多項式時間內為可忽略的函數。在交互式證明系統中，完備性確保當待證明的命題是真時，誠實的證明者幾乎必然能夠說服誠實的驗證者接受其證明，可靠性則是當命題為假時，任何不誠實的證明者幾乎不可能說

服誠實的驗證者接受其證明。

更詳細地說，對于一個k輪的消息交互式證明系統，給定一個將{0，1}n映射到有限范圍的函數f， V和P都被給定一個共同的輸入x∈{0，1}n，在協議開始時，P 提供一個聲稱等于f（x）的值y，由IP指定P，V中的一方來發送第一條消息m1。該方發送消息以后，另一方再發送消息m2，此后消息交替發送，當輪到V發送消息mi時，V是基于輸入{x，m1，m2，…mk，mi-1}產生消息mi。證明者P和驗證者v交換的消息序列與回答y稱為一份transcript ={m1，m2，…mk，y}。在協議的最后，V必須輸出0或1，1表示接受證明者的陳述y=f（x），0表示驗證者拒絕了這一聲稱[13]。

2.1.3 "計算不可區分性：設Dn，En是兩個分布集合，n表示安全參數，如果對任意的非均勻概率多項式算法A滿足下列條件，則這兩集合被稱為計算不可區分：

δ（n） = |Prx ∈Dn[A（x）=1] - Prx ∈ En[A（x）=1]|

2.1.4 "模擬器：設（P，V）是某語言L的一個交互式證明系統，如果對于每個概率多項式時間交互機V*，存在一個概率多項式時間的算法M，使得對于每個x∈L，以下兩個隨機變量是不可區分的，則M被稱為V*與P進行交互的模擬器：

（P，V*）（x）： 在共同輸入x下與交互式機器P交互后交互式機器V*的輸出。

M*（x） ： 機器M*在輸入x上的輸出。

非正式地，模擬器是一臺在不同世界中運行的機器，模擬器雖然不能訪問交互式機器P，但能夠模擬V與P的交互。對于正在評估知識是否被泄露的一方來說，這個世界與現實世界具有不可區分性。

2.1.5 "零知識：隨機變量ViewPV*（x） 表示V*的隨機帶內容和V*在共同輸入x上與P的聯合計算中接收的消息。如果對于每一個概率多項式時間交互式機器V*，存在一個概率多項式時間算法M*使得集合（{ViewPV*（x）}x∈L）和（{M*（x）}x∈L）在計算上不可區分，則稱（P， V）是零知識的。進一步的，零知識證明可分為計算零知識，統計零知識與完美零知識。

2.1.6 "零知識證明（Zero-Knowledge Proofs， ZKPs）：是指具有零知識性的交互式證明系統[14]，具體來說是證明者P和驗證者V之間的一個協議，用于證明一個陳述x屬于語言L。非正式地，這樣的協議必須滿足三個屬性：

完備性：一個誠實的驗證者總是接受一個誠實的證明者對陳述x使用有效見證w所產生的證明。

可靠性：沒有無界的PPT對手可以使一個誠實的驗證者接受一個陳述x L的證明。

零知識性：對于任何陳述x∈L，在多項式時間內可以模擬驗證者和誠實的證明者之間的交互，而不需要知道見證w。

零知識證明作為一項重要的密碼學技術，有著廣泛的應用領域，例如隱私保護、區塊鏈智能合約的驗證等。為了更深入地理解零知識證明的多樣性和適用性，接下來本文將進一步探討零知識證明的不同類型，包括SNARKs（Succinct Non-Interactive Arguments of Knowledge）、STARKs（Scalable Transparent ARguments of Knowledge）以及Bulletproofs等。每種類型都在特定情境下具有獨特的優勢和應用。

2.2 "零知識證明分類

在當前的密碼學研究和實踐中，零知識證明（ZKPs）技術已成為確保數據隱私和完整性的關鍵工具。零知識證明允許一方（證明者）向另一方（驗證者）證明某個陳述的正確性，而無需透露除該陳述正確性之外的任何信息。由于零知識證明底層的構造繁雜，本文更強調零知識證明在區塊鏈上的應用，故本節將深入探討區塊鏈上三種代表性以及使用范圍最廣的零知識證明構造：ZK-SNARK（Zero-Knowledge Succinct Non-Interactive Argument of Knowledge）、ZK-STARK（Zero-Knowledge Scalable Transparent ARgument of Knowledge）和Bulletproof。這三種構造方法體現了零知識證明技術在安全性、效率和實用性方面的不同技術特點及發展趨勢。ZK-SNARK是一種高度壓縮且非交互式的零知識證明，適用于區塊鏈和隱私保護應用。它們的主要優點是極高的驗證效率和低通信開銷，但這種優勢的代價是需要一個可信的設置階段，這可能引入了中心化的風險和潛在的安全漏洞。相比之下，ZK-STARK提供了一種無需可信設置的零知識證明方法，能夠在不犧牲透明度和安全性的前提下提供可擴展性。它利用了密碼學中的哈希函數和其他非對稱技術，因此理論上在對抗量子計算攻擊方面具有更強的韌性。然而，這種方法通常會帶來更大的證明尺寸和計算開銷。最后，Bulletproof是一種新型的非交互式零知識證明技術，不需要可信的設置過程，適用于范圍證明。

綜上所述，ZK-SNARK、ZK-STARK和Bulletproof在各自適用的零知識證明領域扮演著關鍵角色。另外區塊鏈一個顯著的特性就是去中心化。雖然STARK可以被歸為SNARK的一種，但SNARK需要可信第三方設置，而STARK無需此假設。因此，本文仍將STARK與SANRK分開討論。

2.2.1 "ZK-Snark

2.2.1.1 "Snark定義

記R ：= Rλ為一個NP語言LR的高效可判定二元關系。對于對（u， w）∈R稱u為陳述，w為見證。

論證系統：一個對于R的非交互式論證是一個概率多項式算法四元組 Π = （G， P， V， Sim），其定義如下：

CRS生成算法（crs，td）←G（1λ，R）：以某些安全參數 λ，關系 R 作為輸入，輸出一個公共參考字符串crs和一個陷門td。

證明者算法π ←P（crs，u，w）以crs、一個陳述u和一個見證w作為輸入，輸出論證π。

驗證者算法b ←V（ces，u， π）：以一個陳述u和論證π以及crs作為輸入，輸出b = 1表示證明被接受，或輸出b = 0表示證明被拒絕。

模擬器τ ←Sim（crs，td，u）：以一個模擬陷門td和一個陳述u以及crs作為輸入，輸出一個論證τ。

ZK-Snark：一個非交互式論證系統R的ZK-Snark是指滿足以下條件的（G， P， V， Sim）：

完備性：對于關系R的一個真實陳述，一個誠實的證明者 P 擁有一個能夠說服驗證者V有效的證據。更正式地說，對于所有λ∈N和所有 （u， w）∈R，

（Pr[V（crs，u，π） = 1| （crs，td） ← G（1λ，R）， π ← P（crs，u，w）] = 1）

知識可靠性：存在一個提取器，每當對手產生一個有效的論證時，就能計算出一個證據。提取器可以完全訪問對手的狀態，包括任何隨機的硬幣。形式上要求對于所有概率多項式時間（PPT） 對手 A，存在一個PPT提取器（EA）使得

Pr[V（crs，u，π） = 1∧（u，w） "R |（（u， π）;w） ← A| EA（crs）]=negl

簡潔性：一個非交互式論證，其中驗證者在λ + |u| 的多項式時間內運行，并且證明大小是λ的多項式，稱為預處理SNARK。如果公共參考字符串是λ的多項式，則非交互式論證是一個完全簡潔的SNARK。

統計零知識：一個論證是零知識的，如果它不泄露除了陳述真實性的任何信息。形式上，如果對于所有λ∈N，對于所有（u， w）∈R和所有PPT對手A，以下兩個分布統計上是接近的：

D0={π0←P（crs，u，w）： （crs，td）←G（1λ，R）}

D1={π1←Sim（crs，td，u）： （crs，td）←G（1λ，R）}

2.2.1.2 "ZK-SNARK構造

（1）通過PCP模型構造Snark

PCP模型：全稱為Probabilistically Checkable Proofs（概率可檢驗證明），是一種用于描述復雜性類別和證明可驗證性的數學模型。該模型由BABAI L于1991年提出[15]。PCP定理表明，對于NP中的每個問題，存在一個概率多項式時間的證明驗證器，它只檢查證明中的一小部分就能以高概率確定問題的答案。這個發現對于理解NP完全問題的困難性和近似算法的設計具有重大意義。Sanjeev Arora和Shmuel Safra在1998提供了PCP定理的一個更加精確和優化的表述[16]。他們展示了如何構造高效的概率證明檢驗器，這些檢驗器能夠僅通過檢查證明的一小部分來驗證NP完全問題的解決方案。這些發現為計算復雜性理論和近似算法的研究提供了新的視角和工具。

Random Oracle Model： 隨機預言模型（ROM）[17]是一種理想化的密碼模型，它假設存在一個真正的隨機函數-稱為隨機預言機（random oracle）的理想化黑盒。協議的所有參與方都可以訪問該函數。它可以接收任意長度的輸入，并產生相應的隨機輸出。它能夠將任意長度的輸入映射到固定長度的輸出，并且這個映射是隨機的。由于在現實中不存在這樣的理想函數，隨機預言機一般是用散列函數實例化的。

Fiat-Shamir啟發式：Fiat-Shamir變換[18]是一種啟發式方法，可將多輪交互協議轉換為非交互協議或數字簽名，廣泛用于將交互式零知識證明轉換為非交互式零知識證明中。

基于PCP構造Snark的經典協議：Kilian在其1992年的研究[19]中，提出了一種針對NP問題的簡潔零知識論證方法。在這個方法中，證明者P利用Merkle樹為驗證者V提供對PCP證明π的訪問。具體來說，證明者使用抗沖突哈希函數（CRHF）H來計算對長字符串π ∈ {0， 1}^q（λ）的簡潔承諾，并且能夠以簡潔的方式對π的任何比特進行局部開放。證明者首先基于私有輸入和見證w構建一個PCP證明π，然后使用驗證者提供的CRHF H構建一個以π為葉節點值的Merkle樹，從而生成一個根值。證明者將這個根值發送給驗證者，作為對π的承諾。驗證者隨后拋出固定多項式數量的隨機硬幣并發送給證明者。證明者P和驗證者V通過內部運行PCP驗證器對輸入x和根值進行PCP查詢計算。之后，證明者P返回對這些查詢的回答，并附帶“證明”稱為認證路徑－每個回答都與Merkle樹的根保持一致。如果所有回答都與根值一致并且符合PCP驗證器的判斷，驗證者就接受這個證明。由于驗證者V在調用PCP驗證器時只做固定多項式數量的查詢，每個查詢都用固定多項式長度的認證路徑回答，而這些都不依賴于見證的長度，因此Kilian的協議是簡潔的。LIPMAA[20]通過ROM模型將Kilian的四輪交互式協議降低至兩輪交互。Micali[21]通過Fiat-Shamir 啟發式將交互式論證轉換成了非交互式論證[19]，其核心思想是使用哈希函數（被模型化為隨機預言機）處理其概率可檢驗證據（PCP）字符串，這既是一種承諾形式，也用于非交互式地生成驗證者的PCP查詢。Micali結合計算上的可靠性，進一步提高了證明系統的效率，但該方案需要存儲和處理大量數據，導致驗證過程既耗時又占用大量空間。Paul Valiant[22]提出了一個新穎的概念：“增量可驗證計算”。這種方法允許證明者逐步構建證明，證明長時間運行的計算過程是正確的。這種方法適用于復雜或長時間的計算任務，使得在計算的每個階段都能驗證其正確性，而不僅僅在最終階段，能在維持計算正確性的同時減少資源消耗。但上述方案基于PCP的零知識協議構造僅限于理論研究，難以高效實現。Zkboo[23]通過模擬安全多方計算協議的思想，直接構造了高效零知識 PCP，協議的零知識性由安全多方計算協議的隱私性來保障。Zkboo的核心思想本質上是一種基于加性秘密分享機制的具有二元隱私性的多方計算（MPC）協議。Chase減少了驗證者在挑戰響應階段回復的消息數量，在不增加的計算復雜度的同時，將Zkboo的通信復雜度降低了約一半[24]。Chase等同時提出了一種新型的零知識證明和數字簽名方案，這些方案進一步具有后量子安全性，是對傳統的、大多基于非對稱密碼學的零知識證明和簽名方法的重要補充和擴展。此外，構造實現了通信復雜度和驗證者的時間復雜度的降低，其由安全參數中的多項式、實例的大小以及驗證實例的有效證人所需時間的對數限制，從而獲得完全簡潔的SNARK[25]。

（2）通過QAP模型構造Snark

在本節中將探討如何通過QAP來構建SNARK以及一些經典協議。PCP和QAP在目標上有著共同之處：它們都旨在為復雜的計算過程提供一種高效且可驗證的證明機制，同時確保證明的簡潔性和非交互性。PCP提供了強大的理論基礎和廣泛的應用前景，而QAP在某些方面，尤其是在處理算術電路方面，提供了更高的效率和實用性。基于QAP方法的SNARKs用于各種實際應用，包括Zcash [26]等加密貨幣，以通過ZK屬性保證匿名性以及防止雙花問題。

電路滿足問題Circuit-SAT：針對電路C ： Iu ×Iw → {0， 1}，通過關系RC = {（u， w） ∈ Iu ×Iw ： C（u， w） = 1}描述，其語言被定義為LC = {u ∈ Iu ： ?w∈Iw， C（u， w） = 1}。

C-SAT問題屬于NPC（非確定性多項式完全）問題類別，這意味著任何NP（非確定性多項式時間）問題都可以在多項式時間內被轉化為C-SAT問題。同時，多數實際應用中的問題都可以通過電路的方式表達，因此，當前流行的簡潔非交互式零知識證明通常采用C-SAT問題作為待證明命題的表達形式。

二次算術程序QAP：在域F上的二次算術程序Q包含三個多項式集合V={vi（x）}，W={wi（x）}和Y={yi（x）}其中i∈{0， 1， . . . ， m}和一個目標多項式 t（x）。假設F是一個算術函數，它以n個域F的元素作為輸入并輸出 n′ 個元素，總共N = n + n′ 個元素。那么（c1， . . . ， cN ）∈FN 是 F 的有效賦值當且僅當存在系數（cN +1， . . . ， cm）使得 t（x）除以p（x），其中

基于QAP構造的ZKSNARK思路[8]一般是將待證明的陳述規約到C-SAT問題上，再將C-SAT規約至QAP中，直接為C-SAT問題構建零知識證明往往難以實現簡潔性，然后證明者根據CRS模型與其他密碼學方法如承諾的構造，通過找到QAP的解決方案并編碼額外的零知識項來生成證明。其中CRS模型假設存在一個由可信第三方生成的公共字符串，證明者和驗證者可通過訪問該公共字符串生成對應的證明密鑰與驗證密鑰完成非交互的證明與驗證過程。

2010年，Groth[27]基于CRS模型將C-SAT問題簡化為一組方程，并利用雙線性配對來驗證這些方程的有效性。實現了第一個通信量為常數個群元素的 zk-SNARK。2012年Lipmaa[28]成功將協議的CRS大小由電路規模的平方級別降低至O（ClogC）級別。然而證明復雜度仍未降低。在2013年，Gennaro[29]提出了一種新的、有影響力的定義NP復雜性類的方法：Quadratic Span Programs（QSPs）。這是基于Karchmer和Wigderson[30]定義的span programs的自然擴展。QSPs為加密學和理論計算機科學領域提供了一種新的視角，特別是在理解和構造高效的計算表示方式方面。隨后，Lipmaa對QSPs進行了一些變體和改進，他結合現有技術和線性糾錯碼，提出了一類更高效的二次跨度程序[31]。2013年，Gennaro等人[29]提出了QAP，可將算術電路可滿足問題快速歸約為QAP可滿足問題，同時將CRS規模降低至電路的線性級別。Parno提出了Pinocchio[32]，將通信量進一步降低到了8個群元素，且驗證復雜度僅與輸入輸出的大小呈線性關系。Pinocchio協議的優良性能促進了零知識證明的在區塊鏈隱私的第一次大規模落地應用-Zcash。針對布爾電路提出了改進版本的Square Span Programs（SSP）[33]，這自然引導出一種簡化的算術電路版本，即后來的Square Arithmetic Programs（SAP）[34]。這些方法通過緊湊編碼計算，從而獲得高效的零知識SNARKs。它們的核心思想是將每個門的輸入和輸出表示為變量，將每個門重寫為某些表示門輸入和輸出線路的變量的方程。只有符合門邏輯或算術規范的線路值才能滿足這些方程。通過為電路中的所有門組合這樣的約束，任何電路的滿足賦值首先可以被指定為一組二次方程，然后作為一組多項式跨度的約束，定義相應的二次/方形跨度程序。因此，證明者需要說服驗證者，所有的二次方程都是可滿足的，并通過等效多項式找到問題的解決方案。SNARK for QAP使用范圍最廣的技術是Groth在2016年的著名成果[35]，該方案具有完美完備性與完美零知識性。方案在Generic Group Model中實現了三個組元素的證明大小以及3個配對運算的驗證開銷。與Pinocchio中的構造相比，該構造被簡化，且證明元素相對于一些隨機因子并沒有重復且安全性依賴于更強的模型GGM。通用群模型[36，37]是一種理想化的密碼模型，其中算法不利用群元素表示的任何特殊結構，因此可以應用于任何循環群。在這個模型中，攻擊者只能訪問隨機選擇的組編碼，而不是有效的編碼，例如實際使用的有限域或橢圓曲線組所使用的編碼。該模型包括一個執行（加法）組操作的oracle。因此，可以有效地提取用于將預言機的輸出表示為初始組元素的線性組合的系數。此外，Groth提出基于通用非對稱雙線性群模型構建ZK-SNARK的通信度下限，即無法構造通信復雜度僅為1個群元素的 zk-SNARK。然而上述ZK-Snark的構造在初始階段需要一個可信第三方基于某一秘密值生成公共參考串，該秘密值應當在初始階段完成后被誠實丟棄。一旦該秘密值被攻擊者獲取，整個協議就不具備可靠性：證明者可以借助該秘密值偽造證明通過驗證，從而在實際使用中造成巨大的威脅。Ben等人提出第一個ZKP的MPC協議[38]，證明只要至少有一個貢獻方是誠實的，協議生成的CRS就是安全的。

2017年，Bowe 等人提出一種MPC-MMORPG協議，該協議專門針對基于pairing配對的zk-SNARK[39]，如Groth16。在MMORPG協議中，由中央“協調者”管理參與者之間的消息。相較于之前的MPC方案，MMORPG 協議不需要提前選擇貢獻者，也并不總是需要貢獻者隨時在線。此外該協議還確保協調器的公開可驗證性。近些年MMORPG 協議已成為區塊鏈的行業標準。以Ethereum為代表的眾多項目已使用該協議為系統生成CRS。2018年Groth等人的論文提供了一種創新的zk-SNARK協議[40]，它仍利用QAP作為基礎，并具備全局性和可更新性的CRS。在傳統的SNARK協議中，通常需要為每個不同的問題實例生成一個獨立的CRS。這意味著如果有多個不同的問題，就需要為每個問題分別創建和維護一個CRS。2018年，Groth等人引入了CRS的全局性概念[40]，這意味著一個CRS可以用于多個不同的問題實例，而不需要為每個實例重新生成CRS。這種全局性降低了系統的復雜性和計算開銷，使協議更具可擴展性和實用性。另外在傳統的SNARK協議中，CRS是靜態的，一旦生成就不能更改。這導致了一個問題，即如果協議需要適應新的問題實例或更新，就需要重新生成整個CRS，這可能非常耗時和資源消耗。同時Groth還引入了CRS的可更新性，這意味著CRS可以動態地更新，而不需要重新生成。這使得協議能夠在運行時向CRS中添加新的信息，以適應新的問題實例或協議的演化。這種可更新性使協議更加靈活，并且能夠應對不斷變化的需求。但該類CRS的更新在實際中需要額外的預處理過程與相應的更新計算過程，計算開銷往往過大。2019年Maller，Bowe等通過置換論證在代數群模型提高了全局可更新CRS構造的效率，其CRS與電路規模為線性擴展，這使得它在處理復雜計算時更加高效[41]。2020年Plonk進一步改進了Maller等人的成果，顯著提高了證明者的效率，計算要求大大減少[42]。在PLONK中，證明者只需要處理少量的多項式承諾和打開證明，工作量得到了大幅的減少。這種改進對于計算資源受限的應用尤為重要。PLONK的設計允許使用Kate承諾方案有效地驗證多項式方程。這個方案有助于維護零知識特性，并使驗證者能夠有效地檢查一定輸入值范圍內的多項式方程。所以PLONK特別適合于像以太坊上的zk-rollups這樣的應用，解決了主網的吞吐量問題。它已經被用于Aztec[43]項目，該項目專注于以太坊上的隱私保護解決方案。

2.2.2 "ZK-Stark

Eli Ben-Sasson于2018年提出了一種稱為zk- STARKs的新型零知識證明[9]。ZK-STARK是ZK-SNARK協議的改進版本。“STARK”這個縮寫代表“Scalable Transparent ARgument of Knowledge”－即可擴展透明知識論證。“可擴展”指的是證明者的運行時間最多是計算大小的準線性級別、驗證時間是計算大小的對數級別。也就是說，ZK-STARKs是一種針對可用對數空間，使用可計算電路表示陳述的非交互零知識論證。“透明”指的是所有驗證者信息只是公開抽樣的隨機硬幣。ZK-STARK不需要可信設置程序來實例化證明系統，而是依賴于基于哈希沖突的對稱加密算法，這種特性使其更加高效，并且完全擺脫了ZK-SNARK中可信階段產生的參數，能夠有效抗擊量子計算機對算法的威脅。如之前所說，非交互式 STARK是SNARK的一個子類，用來指特定的可擴展透明SNARK構造。ZK-Stark通過AIR（algebraic intermediate representation，代數中間表示）進行約束的表示，STARK證明系統將在任何時間計算的狀態都包含在從有限域取值的寄存器元組中，在每個周期更新狀態。而代數執行軌跡（AET）則是按時間順序排列的所有狀態元組的列表。通過AIR定義了對代數執行軌跡的兩種類型的約束：邊界約束（在計算的開始或結束時，指示的寄存器具有給定的值）與轉換約束（任何兩個連續的狀態元組都按照狀態轉換函數演變）。FRI（Fast Reed-Solomon IOP）是一種協議，其中證明者發送對應于編碼的Merkle根序列，該編碼的長度在每次迭代中減半；驗證者通過證明者提供的葉子及其認證路徑檢查連續輪的Merkle樹以測試簡單的線性關系。對于誠實的證明者，所表示的多項式的次數同樣在每一輪中減半，并且因此比編碼的長度小得多。然而，對于惡意的證明者，這個長度僅比編碼的長度小一些。不斷重復該過程，在最后一步中，證明者發送對應于常數多項式的非平凡編碼。這樣通過AIR與FRI，得到了一個交互式的證明系統，再通過Fiat-Shamir變換可最終得到一個非交互式的STARK證明。ZK-STARKs可以有一個非常快的證明時間和驗證時間，但證明大小過大。因此，它在投票系統、在線系統和其他一些需要識別步驟才能訪問的服務中有著光明的前景。

2.2.3 "Bulletproof

Bulletproof的構造思路如下：首先將電路中的乘法門約束和乘法門之間的線性約束利用Schwartz- Zippel引理[44]歸約為一個多項式的某一特定項系數為零的問題，然后將該問題轉化為內積論證（IPA）[45]的陳述表示形式，最后調用內積論證實現零知識證明。

Bulletproof提供了一種更有效的機密交易（CT）范圍證明，主要應用于在加密貨幣領域如Zcash中。防彈技術建立在實現通信高效的零知識證明的技術之上，它們可以用來擴展多方協議，如多重簽名或零知識緊急支付等，事實上，Bulletproof可以認為是基于IPA的Snark構造的一種。Bootle將C-SAT問題歸約為一個多項式是否為零多項式的問題[46]，然后調用內積論證實現對數級別的通信復雜度，但在進行對目標多項式承諾這一步驟時，Bulletproofs通過消除Bootle工作[46]的一些多項式計算過程，只需分別對每一項系數進行承諾，從而降低證明者的計算開銷，將目標多項式的次數降低至常數。Hoffmann指出 Bulletproofs 中門的約束關系可轉化R1CS的表述形式，再通過二次等式（quadratic equations） 表達約束來降低證明者的計算開銷，并通過實驗證明計算開銷約是Bulletproofs的3/4[47]。然而上述協議的驗證者復雜度都是線性級別，而且需要大量的群冪運算，在實際應用中的開銷過大。Daza將驗證者的復雜度從線性降到了對數級別，增加了實際的可用性[48]。

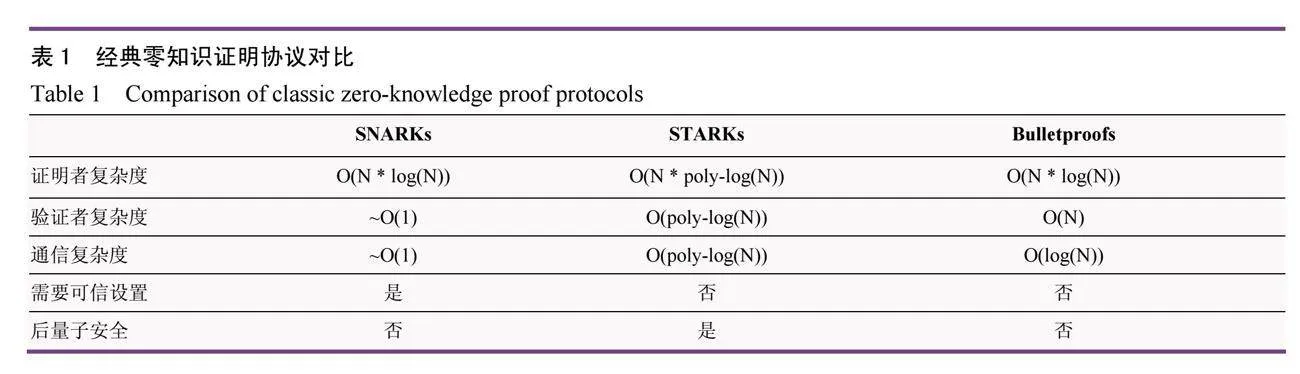
2.3 "區塊鏈上經典零知識證明協議對比

本節對上述三種零知識證明協議進行了分析與對比，如表1所示，在證明者的算法復雜度方面，SNARKs和Bulletproofs都需要O（N*log（N））的復雜度，而STARKS僅需要O（N*poly-log（N））的復雜度，這表明STARKs在證明的構建上可能有更高的效率，尤其是在處理大量數據時。對于驗證者，SNARKs擁有最低的復雜度，幾乎是常數時間（～O（1）），這使得它們在驗證證明時非常高效。通信復雜度是指生成的證明大小，SNARKs在這方面也表現出極高的效率，其證明大小幾乎是常數（～O（1）），而STARKs和Bulletproofs的證明大小隨著數據量的增加而緩慢增長。在零知識證明的安全性方面，需要可信設置的協議可能存在中心化的風險，SNARKs在這方面需要可信設置，而STARKs和Bulletproofs不需要，這使得后兩者在去中心化和安全性方面更為可靠。另外，只有STARKs是后量子安全的，這意味著它們能夠抵抗未來量子計算機的攻擊，而SNARKs和Bulletproofs在這方面存在潛在的安全隱患。

每種協議都有其優勢和劣勢，SNARKs在證明者和驗證者的算法復雜度以及通信復雜度上表現出色，但需要可信設置，并且不是后量子安全。STARKs雖然在證明構建時復雜度較高，但不需要可信設置且是后量子安全，是一種在安全性和未來兼容性方面表現良好的協議。Bulletproofs在證明大小上具有優勢，但在驗證者的復雜度上不如SNARKs和STARKs，且同樣不是后量子安全。

3 "零知識證明的應用

現有的關于零知識證明的研究綜述[7，14]，往往在應用研究方面不夠深刻，有時過于關注理論的完整性，而忽視了零知識證明在實際應用中的具體功能和實現，無法深入到具體的應用層面，或者在實際應用案例中無法提供詳盡的分析。比如對于區塊鏈的擴容問題，已成為增強區塊鏈網絡可擴展性的關鍵方案。Rollups通過在二層協議上處理交易并將結果傳回主鏈，能夠在提高性能和降低交易費用的同時，保持去中心化和安全性。在這一過程中，零知識證明尤為關鍵，因為它們允許在主鏈上對多筆交易的真實性進行一次性驗證，而無需逐個驗證每筆交易的細節。這降低了計算和存儲成本，并且可以確保所有的交易都經過了正確的驗證，避免了虛假交易的問題。而在跨鏈技術方面，ZK Bridge展示了零知識證明技術在實現不同區塊鏈之間資產與信息傳遞的潛力。與傳統的跨鏈橋相比，ZK Bridge的優勢在于它不需要引入額外的信任假設，并且可以實現高效率的交易驗證，從而降低了計算和存儲成本。所以總體而言，零知識證明在區塊鏈應用中的實際落地不僅涉及技術實現，還包括了設計理念和效率問題。當前的零知識證明相關的應用綜述文獻[49]缺少對于零知識證明在跨鏈的應用場景的分析與討論，而跨鏈已成為零知識證明在區塊鏈中的重要應用場景之一。因此，本節將會對于擴容與跨鏈這兩個具體的應用領域進行分析。另外Bulletproof往往應用在機密交易的場景中，如Zcash，Monero[50]中，它能隱藏交易金額的同時驗證交易的合法性，機密交易通過隱藏交易雙方的金額來提高隱私性，但傳統的方法往往會導致證明的大小與交易數量線性增長，這對區塊鏈的擴展性和效率構成挑戰。Bulletproofs技術的引入改善了這一狀況，因為它生成的范圍證明既短小也高效，證明的大小與交易金額的位數呈對數關系，而非線性關系。這意味著即使在處理大量交易時，也能顯著減少數據的存儲和處理需求。此外，如上文所說Bulletproofs在保證交易隱私的同時無需trusted setup，也就是說，在生成零知識證明時無需一個可信的第三方來初始化系統，這消除了中心化的風險，并且在某種程度上提高了系統的安全性。由于本節專注于零知識證明在擴容與跨鏈的應用領域，故本節不再單獨針對Bulletproof的應用進行說明。

3.1 "擴容

Layer 1是指基礎的區塊鏈協議如比特幣和以太坊，構成了區塊鏈的基礎架構，它們負責處理網絡的基本功能，包括交易驗證、共識機制的實施以及保證數據的不可逆性。然而，隨著網絡參與者的增加和應用的豐富，原有的Layer 1技術開始顯得不夠用，主鏈的擁堵和高昂的交易費用成了限制區塊鏈大規模應用的瓶頸。

Layer 2是建立在Layer 1基礎之上的網絡，旨在通過處理鏈外交易來提升擴展性。Layer 2解決方案可以在不直接修改L1協議的情況下，實現交易速度的提升和成本的降低。Layer 2技術通常包括狀態通道、側鏈和Rollup等。

隨著以太坊生態的日漸繁榮，以太坊主鏈無法承受龐大的生態，導致整個以太坊網絡擁堵。Rollup是為了緩解Layer1擴容問題所提出的可擴展性的方案，通常被稱為鏈下解決方案。它擴展了以太坊并繼承了以太坊的安全保證。它的主要目的是在提高以太坊的性能并且降低 Gas費用的同時，保留分布式協議的去中心化和安全性特點。Rollup通過將Layer1的部分數據轉移到二層協議上進行處理，然后將處理結果返送到Layer1上，從而增強區塊鏈網絡的可擴展性。Rollups會在其上的網絡中將交易打包在一起并進行壓縮，然后將打包后的交易發送到Layer1主網進行驗證，通過一次性驗證多筆交易，使得網絡效率得到提高，同時增加了可被執行的交易數量，實現了網絡擴容。但在這個過程中，需要保證L1的節點沒有作弊上傳虛假交易。根據證明方法，Rollup 可以大致分為兩類：樂觀（optimistic）—Rollup 和ZK（零知識）-Rollup。Optimistic-Rollup的前提是所有交易均有效，除非另有證明。如果交易的有效性受到質疑，驗證者需要提供欺詐證明，然后將其發送到主網絡進行驗證。如果發現無效，交易將被恢復。這種方法依賴于網絡參與者彼此保持誠實，從而建立信任和警惕的平衡。但是當用戶提供欺詐證據時，主網上的解決方案不會立即得到解決。這可能會導致從Optimistic-Rollu鏈中提取資產時出現延遲，等待時間從幾天到甚至幾周不等。而零知識證明可以很好地完成上述需求，在L1打包多筆交易后同時為這個過程生成零知識證明，驗證者在Layer1上通過驗證該證明后打包生成共識，完成擴容功能。ZK-Rollup則確保所有交易都經過驗證，同時保持交易詳細信息完全私密。這不僅增強了安全性，而且提供了所有用戶都非常贊賞的更高程度的隱私。ZK-rollups 還提供近乎即時的事務驗證，使Optimistic-Rollup在速度方面無法與之相比。ZK-rollups的落地應用包括基于Snark的Scroll[51]，基于Starknet的Starknet[52]，混合Snark與Stark證明機

制的Taiko[53]等項目。

3.2 "跨鏈

跨鏈技術是一種使得加密資產在不同的區塊鏈之間移動和儲存的技術。當前市場上存在眾多獨立運作的區塊鏈，例如比特幣和以太坊，但它們之間缺乏直接的互通機制。若無跨鏈技術，資產將無法在不同鏈間轉移。跨鏈技術旨在實現不同區塊鏈間資產與信息的互傳遞，打破不同區塊鏈間的壁壘，促進了資產和數據的交流，同時提高了網絡的性能和功能，更好地滿足用戶需求。

ZK Bridge作為使用零知識證明技術的跨鏈橋梁，其最大特點是不需要引入額外的信任假設就可以適應多種不同類型的區塊鏈。在這個解決方案當中，零知識證明是在區塊鏈之外生成的，實際的驗證則是在區塊鏈上進行的。這樣的做法大幅降低了區塊鏈上的計算和存儲成本，是當今市場上一種相當前沿且有潛力的跨鏈技術。目前，有幾個項目正在發展ZK Bridge 的生態系統，也就是開發基于零知識證明技術的跨鏈橋解決方案，但皆處于開發階段。例如，Succinct Labs[54]、Electron Labs[55]、zkIBC[56]、Polyhedra Network[57]的 zkBridge[58] 等。Succinct Labs推出了Tendermint X，這是第一個開源的、高性能的Tendermint ZK輕客戶端，它為Cosmos和Ethereum之間提供了一個無需信任的ZK橋接，標志著將Cosmos連接到Ethereum的實現，為超過4000萬美元的TVL和超過15億美元的穩定幣資產流動提供了安全保障。ZKIBC，即基于零知識證明的區塊鏈間通信協議，是一項創新技術，專門設計來解決現有區塊鏈互操作性方案中的隱私和安全問題。ZKIBC的核心，是對跨鏈交易中數據的處理方式的重新思考。傳統的區塊鏈互操作方案通常需要在鏈上公開交易的某些細節，以便進行驗證。而zkIBC通過構造特定的零知識證明，只向驗證者證明交易的合法性（例如，證明者擁有足夠的資金進行交易），而不暴露交易的具體細節（如交易金額、資產來源等）。這種方法的一個關鍵優點是，它大大減少了鏈上的信息泄露風險，提高了參與雙方的隱私保護。相比較與前兩者，Polyhedra Network的zkBridge利用其獨創的deVirgo協議，一種高效的分布式零知識證明協議，實現了令人印象深刻的性能優化和線性可擴展性。deVirgo協議的核心優勢在于它幾乎完美的線性可擴展性—在一個分布式計算網絡中，隨著計算資源的線性增加，證明的生成時間將成倍減少。具體來說，如果網絡擁有M臺計算機，那么生成證明的時間可以減少近M倍。這樣的設計使得Polyhedra Network的Layer1能力得到顯著地擴展，為區塊鏈應用提供了前所未有的擴展性和效率。deVirgo協議的這一特性特別適合處理大量數據或高頻交易，使得zkBridge在處理跨鏈交易時，不僅保持了零知識證明的隱私和安全性優勢，同時也確保了極高的吞吐量和低延遲，這對于金融交易和復雜的去中心化應用（dApps）來說至關重要。

這些項目都充分利用zk-SNARKS 技術來革新跨鏈橋的設計。此外，ZK Bridge在效率方面帶來了明顯的優勢。傳統的跨鏈交易驗證往往需要大量的計算和存儲資源，導致交易速度緩慢且耗能巨大。然而，通過使用 zk-SNARKs 技術，ZK Bridge在跨鏈交易驗證過程中能夠實現高效率地驗證，減少了計算和存儲的負擔。這種高效率使得交易得以快速驗證和確認，從而加快整個跨鏈交易過程。同時ZK Bridge還可以在不犧牲安全性的前提下實現快速驗證，這在高頻交易環境下尤其有利。傳統的跨鏈解決方案常常受限于交易的規模和速度，很難應對不斷增長的用戶需求。而通過應用zk-SNARKs技術，ZK Bridge能夠實現較小的驗證負荷，從而實現更好的擴展性。這種擴展性使得ZK Bridge能夠應對大規模交易的處理需求，并且在未來的發展中能夠輕松擴展以適應不斷變化的市場。

4 "零知識證明相關工具庫

在探討零知識證明（ZKP）相關的開發庫和領域特定語言（DSL）時，理解它們在電路生成中的作用至關重要。這些方案的能效往往取決于電路大小，通常以門的數量來衡量。因此，電路生成是影響整體性能的關鍵因素之一。計算的轉化可以通過手動電路構造工具或利用編譯器自動完成。盡管手動轉化可能產生更優化的電路，高級編譯器則為開發者提供了更多便利。在性能敏感的應用中，低級電路構造工具通常更為重要。

4.1 "高級編譯器

高級編譯器為開發人員提供了一種將計算轉換為電路的簡單方法。這些編譯器接受用高級語言編寫的代碼。因此，新的和現有的算法都可以很容易地轉換。然而，為了產生足夠大小的電路，它們可能已經對代碼的結構施加了一些限制。

TinyRAM：這是一種用于表達非確定性計算正確性的隨機存取機器，特別是在簡潔的零知識證明環境中。它旨在將計算任務表示為可以高效驗證的形式。TinyRAM設計為一個簡化指令集計算機（RISC），具有字節級和字級可尋址的隨機存取存儲器。

Geppetto：這是一個全面的可驗證計算框架，它實現了一個可擴展的編譯器和運行時環境，可以處理從各種源C程序和密碼學庫生成的LLVM代碼。這個框架在由云計算引發的對可驗證計算協議的興趣中誕生，這些協議允許計算能力較弱的客戶端將計算任務安全地外包給遠程方。Geppetto引入了互補技術來減少證明者的開銷并增加證明者的靈活性。通過Multi-QAPs，Geppetto大幅降低了在計算之間（例如，MapReduce）或在單個計算內共享狀態的成本，其降低程度高達兩個數量級。通過仔細選擇密碼學原語，Geppetto也降低了驗證外包加密計算的成本（例如，可驗證地計算簽名數據）。

ZoKrates：這是一個面向以太坊的zkSNARKs工具箱，它幫助用戶在DApp中使用可驗證計算，從用高級語言編寫程序的規范，到生成計算證明，再到在Solidity中驗證這些證明。它通過一個特定領域的語言、一個編譯器以及用于生成證明和驗證智能合約的生成器，簡化了零知識證明固有的復雜性，為開發人員提供了更熟悉和更高級的編程接口。ZoKrates將離鏈程序與以太坊區塊鏈聯系起來，擴展了DApp的可能性。

genSTARK：這是一個基于JavaScript的庫，用于生成基于STARK（Scalable Transparent ARguments of Knowledge）的零知識證明。它旨在幫助用戶快速輕松地生成計算的STARK證明。genSTARK盡可能地處理模板代碼，讓用戶能夠專注于計算的具體細節。

Sdiehl：這是一個純Rust語言實現的Bulletproofs庫，使用了Ristretto來提高安全性和性能。適用于證明關于承諾值的語句，例如范圍證明、可驗證混洗、算術電路等，支持單范圍和多范圍證明。

4.2 "低級電路構造工具

在零知識證明方案中，性能是一個關鍵因素，尤其當方案的效率至關重要時，低級電路構造工具成為必不可少的資源。相較于高級編譯器，這些工具要求開發者直接手動編寫電路或約束，這一過程雖然復雜度較高，但由此生成的電路往往更為精簡和高效。通過細致地設計電路，可以顯著減少所需的門數量，進

而提升整個零知識證明系統的性能。

libSNARK：這是一個C++庫，為zkSNARKs證明的創建和驗證提供了高效地實現，使得證明的創建和驗證過程非常迅速。它還包含了一套靈活的構建工具，允許開發者從底層開始構建復雜的約束系統實例。libsnark的設計注重于性能和安全性，雖然它是研究級別的概念驗證，并且未經過廣泛的審查或測試，但其理論安全性建立在詳盡分析過的數學構造上。此外，libsnark還提供了一系列“gadget”庫，可以方便地構建可重用的“gadget”以及額外的顯式方程。這些庫基于模板設計，以便高效地支持在多個橢圓曲線上工作。對于開發者而言，libsnark是一個強大且靈活的工具，能夠幫助他們在保護隱私的同時，實現復雜的密碼學協議。

jsnark：它允許用戶用Java編程語言直接構建和操作zk-SNARK電路。jsnark的主要目的是簡化在Java環境中開發zk-SNARK應用程序的過程。作為一個研究工具，它為零知識證明提供了一個可訪問和靈活的開發平臺。

Bellman：這是一個基于Rust的庫，用于約束系統的公式化。它提供了電路特性和基本結構，以及諸如布爾值和數字抽象等基礎gadget的實現。Bellman使用ff和group crates在標量字段類型上通用構建電路。Bellman的目的是使zk-SNARK的使用和實驗對普通公眾更加易于訪問，同時提高下一代Zcash的安全性和性能。在Bellman中，所有的電路抽象都是通用編寫的，涵蓋了橢圓曲線和有限域算術。電路合成的核心是ConstraintSystem trait，負責變量的分配、賦值和約束的執行。

Circom：這是一個為零知識證明（ZKPs）設計的領域特定語言（DSL），專門用于在區塊鏈和密碼學應用中構建和驗證算術電路。它為開發者提供了一個強大的工具鏈和生態系統，以滿足零知識密碼學的具體需求，特別是在以太坊生態系統中的應用。Circom的核心在于能夠將計算問題轉換成算術電路的形式，這些電路隨后可以用于生成零知識證明。Circom 通過其特有的語法和結構，使得開發者能夠方便地創建和表示計算邏輯。它支持信號和約束系統，其中計算被模型化為一組多項式方程，稱為 Rank-1 Constraint System（R1CS）。這使得 Circom 不僅能夠處理簡單的算術運算，還能處理更復雜的密碼學函數和算法。此外，Circom 引入了模板和組件的概念，允許開發者以模塊化和可擴展的方式構建電路。這些模板提供了一種參數化結構，使得特定值的電路實例化成為可能，而組件則用于定義具有輸入和輸出信號的算術電路。Circom 的另一個重要特點是支持并行化計算，這在處理大型電路時特別有益，可以提高見證生成的效率。Circom 與 zkSNARK 生成器（如 snarkjs）緊密協作，將復雜的高級約束翻譯成適合 zkSNARK 的格式，從而創建零知識證明系統中的證明者和驗證者。

gnark：這是適用于Go語言的開源庫，用于編寫零知識參數協議的電路。

目前已有多個零知識證明的開發框架已被基準測試，以比較它們的性能。例如，Circom、gnark和Arkworks都采用相同的R1CS算術化，而Halo2和Plonky2則采用Plonkish算術化。Starky使用AIR算術化，而Boojum則基于特定優化達到了較少的約束數量。

5 "挑戰與未來展望

零知識證明仍然面臨許多挑戰，同時也帶來了許多研究方向。具體如下：

較弱假設的挑戰：ZKP的一個挑戰是，是否可以在一些較弱假設下有效實施。例如，Zerocash中使用了zkSNARK，但它需要一個受信任的第三方來進行設置和系統初始化。ZKP可以在沒有受信任第三方的情況下實施，但這會影響ZKP的效率。因此，研究在沒有受信任第三方的情況下有效實施ZKP是值得的。Spartan是一個引人注目的成果[59]，它提供了一種無需可信設置的zk-SNARKs，特別適用于解決算術電路滿足性問題（R1CS）。它的特點在于，它能夠在驗證證明時產生低于線性的成本，而且不要求NP陳述的結構具有一致性。此外，Spartan實現了時間最優化的證明者，這在先前的zk-SNARKs文獻中幾乎未被實現。Spartan應用了新技術，如計算承諾和一個加密編譯器SPARK，用于將現有的可提取多項式承諾方案轉換為有效處理稀疏多項式的方案，這對于實現時間最優化的證明者至關重要。Spartan作為Rust庫實現，并與最新zkSNARKs進行了實驗比較，表現出多方面的優勢，包括在無可信設置方案中具有較快的證明者速度，生成更短的證明，驗證時間低，綜合效率優秀。

不同機制的融合：每種ZKP模型都有其獨特的優勢，當前研究的趨勢是尋找將這些不同ZKP模型的優勢結合起來的方法。比如Orion[60]等，正在探索如何更有效地結合不同的ZKP模型來提高交叉鏈互操作性和整體系統性能。

效率優化：在現有的ZKP模型中，效率優化方法通常適用于在足夠大的域上的算術電路。研究是否存在一種新的效率優化方法，適用于在一些小域或布爾電路上的算術電路，是值得的。同時，這種可能的方法不應該需要任何額外的計算開銷。此外，這種方法與減小域大小相關聯，且不會影響證明的正確性。

其他數學問題：目前，為了提高ZKP的效率，大多數優化方法專注于雙線性群的計算研究，研究依賴于其他數學問題來構建高效的非交互式ZKP模型的可能性是值得的。一個突破性的進展是QuickSilver協議[61]。該協議在電路基礎模型中，將計算表示為一個場上的電路，實現了每個非線性門僅需一個場元素的通信復雜性，同時保持了非常低的計算成本。QuickSilver的實現表現出極高的效率和可負擔性。相比之前最佳的實現，它在計算上實現了6倍至7倍的提升，在通信上實現了3倍至7倍的提升。這表明在處理小域或布爾電路上的算術電路時，QuickSilver提供了一種高效的優化方法。

基于格的密碼學：公鑰密碼算法是在區塊鏈環境中構建ZKP模型的關鍵因素。不幸的是，常見算法無法抵抗量子計算攻擊，特別是考慮到量子計算對傳統公鑰密碼算法的潛在威脅。例如，RSA算法可以被量子計算中的Shor算法在多項式時間內破解。然而，基于格的密碼學問題，如模塊-SIS和模塊-LWE問題，被認為對量子攻擊具有抵抗力。最近的研究提出了一個改進的實用協議[62]，用于證明知道滿足As=t mod q的短向量s。該協議提供了一種更直接且更高效的方式來證明s的系數具有小的2范數，不需要轉換到CRT表示。這項新的證明系統可以被黑箱方式插入到各種基于格的隱私原語的構造中，例如可驗證的加密方案和群簽名方案，使得解決方案比以前的最佳解決方案緊湊兩倍以上。

零知識證明的硬件加速：零知識證明技術雖然被廣泛認為是解決區塊鏈主要問題的關鍵方案，但長期受制于其本身的高計算密集性導致的計算效率問題。正是基于這種背景，ZKP硬件加速成為解決ZKP效率問題的一個重要創新方向。ZKP硬件加速涉及在專用硬件（如 GPU、FPGA和ASIC）上實現ZKP算法的優化，使其能夠更快地處理復雜計算，從而大幅提高 ZKP 的生成和驗證速度。在 ZKP 的不同證明系統及其相關實現中，計算需求與資源開銷各不相同。在眾多證明系統中，有兩種計算操作尤為耗時與昂貴，分別是多標量乘法（Multiscalar Multiplication-MSM）和快速傅里葉變換（Fast Fourier Transform-FFT）。CUZK[63]中提出MSM算法占據了證明生成總運行時間的70%以上。隨著新的ZKP框架STARK的發展，也有更多的證明是基于FTT算法為主。

多標量乘法（MSM）是一種在橢圓曲線密碼學中常見的操作，它涉及對多個標量和橢圓曲線點的乘法與求和運算。雖然MSM 可以通過并行處理來加速，但即使在多核心的系統上，對于復雜的應用MSM 的運算仍然需要消耗大量的資源與時間。MSM 算法需要處理大量的元素與重復執行相同的操作。

以STARK為代表的零知識證明系統大量用到了快速傅里葉變換（FFT）。這個算法用于高效計算序列的離散傅里葉變換（DFT）及其逆變換。FFT 的運行過程嚴重依賴于數據的頻繁交換，數據交換過程中需要從大數據集中“隨機”地傳輸元素，這在硬件內存有限的情況下尤為困難。盡管硬件操作本身非常快，但傳輸數據的時間卻顯著降低了整體操作速度。除此之外，FFT 算法通常需要將輸入數據重新排列成特定順序以執行變換，這可能需要大量的數據移動，對于大型FFT算法規模來說，這可能成為性能瓶頸。FFT 雖然是一種強大且廣泛應用的算法，但在大型數據處理和分布式計算環境中，其性能和效率受到數據交換、帶寬限制的顯著影響。

基于SNARK的證明系統主要依賴于MSM算法，而STARK類證明則主要使用FFT算法。因此，目前的硬件加速主要是面向這兩種加密算法的需求進行優化。MSM 對硬件的需求包括強大的并行處理能力、較大的內存容量。相比之下，FFT對硬件的需求則包括高帶寬、大內存容量、高效的數據訪問模式。

6 "結語

本文中首先深入剖析了零知識證明的核心原理，并概述了Snark、Stark等不同類型的ZKPs，展現了它們獨特的技術特性和應用場景。本研究特別深入探討了ZK-Snarks的理論基礎，如PCP和QAP，并分析了它們在構建零知識證明過程中的關鍵作用。同時，也將ZK-Snarks和ZK-Stark、Bulletproofs等其他證明機制進行了比較，揭示了它們在設計和性能上的獨特優勢。隨后，詳細介紹了ZKP在區塊鏈技術中的應用，包括在確保交易隱私和數據安全性方面的潛力，并綜合分析了開發零知識證明相關工具的實踐方法，如Circom、ZoKrates以及其他低級電路構造工具的使用。特別強調，盡管零知識證明技術已經取得了顯著進展，但在實現廣泛應用方面仍面臨挑戰，這包括對零知識證明算法的進一步優化、對電路構造工具的改進以及對新應用場景的開發。文章最后提出了一些潛在的研究問題，并展望了零知識證明技術在加強數據隱私保護和推動區塊鏈技術發展方面的未來方向。

參考文獻

[1] Nakamoto S. Bitcoin： A peer-to-peer electronic cash system[J]. Computer Science，2008. DOI：10.2139/ssrn.3440802.

[2] Buterin V. A next-generation smart contract and decentralized application platform[J]. White Paper， 2014， 3（37）： 2-1.

[3] Badreddine W， Zhang K， Talhi C. Monetization using blockchains for IoT data marketplace[C]//2020 IEEE International Conference on Blockchain and Cryptocurrency. IEEE， 2020： 1-9. DOI：10.1109/ ICBC48266.2020.9169424.

[4] Rivest R L， Adleman L， Dertouzos M L. On data banks and privacy homomorphisms[J]. Foundations of Secure Computation， 1978， 4（11）： 169-180.

[5] Rivest R L， Shamir A， Tauman Y. How to leak a secret[C]//Advances in Cryptology—ASIACRYPT 2001： 7th International Conference on the Theory and Application of Cryptology and Information Security Gold Coast， Australia， December 9–13， 2001 Proceedings 7. Springer Berlin Heidelberg， 2001： 552-565.

[6] Yao A C. Protocols for secure computations[C]//23rd Annual Symposium on Foundations of Computer Science .IEEE， 1982： 160-164.

[7] 李一聰，周寬久，王梓仲.基于零知識證明的區塊鏈隱私保護研究[J].空間控制技術與應用，2022，48（1）：44-52.

[8] Goldwasser S， Micali S， Rackoff C. The knowledge complexity of interactive proof systems[J]. SIAM Journal on Computing， 1989， 18（1）： 186-208.

[9] Ben-Sasson E， Bentov I， Horesh Y， et al. Scalable zero knowledge with no trusted setup[C]//Advances in Cryptology–CRYPTO 2019： 39th Annual International Cryptology Conference， Santa Barbara， CA， USA， August 18–22， 2019， Proceedings， Part III 39. Springer International Publishing， 2019： 701-732.

[10] Gong Y， Jin Y， Li Y， et al. Analysis and comparison of the main zero-knowledge proof scheme[C]//2022 International Conference on Big Data， Information and Computer Network （BDICN）. IEEE， 2022： 366-372.

[11] Bünz B， Bootle J， Boneh D， et al. Bulletproofs： Short proofs for confidential transactions and more[C]//2018 IEEE symposium on security and privacy （SP）. IEEE， 2018： 315-334.

[12] Goldreich O. Foundations of Cryptography， Volume 2[M]. Cambridge： Cambridge University Press， 2004.

[13] Nitulescu A. zk-SNARKs： a gentle introduction[J]. Computer Science， 2020.

[14] 李威翰，張宗洋，周子博等.簡潔非交互零知識證明綜述[J].密碼學報，2022，9（3）： 379-447.

[15] Babai L， Fortnow L， Levin L A， et al. Checking computations in polylogarithmic time[C]//Proceedings of the twenty-third annual ACM symposium on Theory of computing[J]. Computer Science， 1991： 21-32.

[16] Arora S， Safra S. Probabilistic checking of proofs： A new characterization of NP[J]. Journal of the ACM （JACM）， 1998， 45（1）： 70-122.

[17] Bellare M， Rogaway P. Random oracles are practical： A paradigm for designing efficient protocols[C]//Proceedings of the 1st ACM Conference on Computer and Communications Security. 1993： 62-73.

[18] Fiat A， Shamir A. How to prove yourself： Practical solutions to identification and signature problems[C]//Conference on the theory and application of cryptographic techniques. Berlin， Heidelberg： Springer Berlin Heidelberg， 1986： 186-194.

[19] Kilian J. A note on efficient zero-knowledge proofs and arguments[C] //Proceedings of the twenty-fourth annual ACM symposium on Theory of computing. 1992： 723-732.

[20] Di Crescenzo G， Lipmaa H. Succinct NP proofs from an extractability assumption[C]//Logic and Theory of Algorithms： 4th Conference on Computability in Europe， CiE 2008， Athens， Greece， June 15-20， 2008 Proceedings 4. Springer Berlin Heidelberg， 2008： 175-185.

[21] Micali S. CS proofs[C]//Proceedings 35th Annual Symposium on Foundations of Computer Science. IEEE， 1994： 436-453.

[22] Valiant P. Incrementally verifiable computation or proofs of knowledge imply time/space efficiency[C]//Theory of Cryptography： Fifth Theory of Cryptography Conference， TCC 2008， New York， USA， March 19-21， 2008. Proceedings 5. Springer Berlin Heidelberg， 2008： 1-18.

[23] Giacomelli I， Madsen J， Orlandi C. {ZKBoo}： Faster {Zero- Knowledge} for Boolean Circuits[C]//25th USENIX Security Symposium （USENIX Security 16）. 2016： 1069-1083.

[24] Chase M， Derler D， Goldfeder S， et al. Post-quantum zero-knowledge and signatures from symmetric-key primitives[C]//Proceedings of the 2017 ACM Sigsac Conference on Computer and Communications Security. 2017： 1825-1842.

[25] Bitansky N， Canetti R， Chiesa A， et al. The hunting of the SNARK[J]. Journal of Cryptology， 2017， 30（4）： 989-1066.

[26] Sasson E B， Chiesa A， Garman C， et al. Zerocash： Decentralized anonymous payments from bitcoin[C]//2014 IEEE symposium on security and privacy. IEEE， 2014： 459-474.

[27] Groth J. Short pairing-based non-interactive zero-knowledge arguments[C]//Advances in Cryptology-ASIACRYPT 2010： 16th International Conference on the Theory and Application of Cryptology and Information Security， Singapore， December 5-9， 2010. Proceedings 16. Springer Berlin Heidelberg， 2010： 321-340.

[28] Lipmaa H. Progression-free sets and sublinear pairing-based non- interactive zero-knowledge arguments[C]//Theory of Cryptography： 9th Theory of Cryptography Conference， TCC 2012， Taormina， Sicily， Italy， March 19-21， 2012. Proceedings 9. Springer Berlin Heidelberg， 2012： 169-189.

[29] Gennaro R， Gentry C， Parno B， et al. Quadratic span programs and succinct NIZKs without PCPs[C]//Advances in Cryptology- EUROCRYPT 2013： 32nd Annual International Conference on the Theory and Applications of Cryptographic Techniques， Athens， Greece， May 26-30， 2013. Proceedings 32. Springer Berlin Heidelberg， 2013： 626-645.

[30] Karchmer M， Wigderson A. On span programs[C]//[1993] Proceedings of the Eigth Annual Structure in Complexity Theory Conference. IEEE， 1993： 102-111.

[31] Lipmaa H. Succinct non-interactive zero knowledge arguments from span programs and linear error-correcting codes[C]//Advances in Cryptology-ASIACRYPT 2013： 19th International Conference on the Theory and Application of Cryptology and Information Security， Bengaluru， India， December 1-5， 2013， Proceedings， Part I 19. Springer Berlin Heidelberg， 2013： 41-60.

[32] Parno B， Howell J， Gentry C， et al. Pinocchio： Nearly practical verifiable computation[J]. Communications of the ACM， 2016， 59（2）： 103-112.

[33] Danezis G， Fournet C， Groth J， et al. Square span programs with applications to succinct NIZK arguments[C]//International Conference on the Theory and Application of Cryptology and Information Security. Berlin， Heidelberg： Springer Berlin Heidelberg， 2014： 532-550.

[34] Groth J， Maller M. Snarky signatures： Minimal signatures of knowledge from simulation-extractable SNARKs[C]//Annual International Cryptology Conference. Cham： Springer International Publishing， 2017： 581-612.

[35] Groth J. On the size of pairing-based non-interactive arguments[C] //Advances in Cryptology–EUROCRYPT 2016： 35th Annual International Conference on the Theory and Applications of Cryptographic Techniques， Vienna， Austria， May 8-12， 2016， Proceedings， Part II 35. Springer Berlin Heidelberg， 2016： 305-326.

[36] Shoup V. Lower bounds for discrete logarithms and related problems[C]//Advances in Cryptology-EUROCRYPT’97： International Conference on the Theory and Application of Cryptographic Techniques Konstanz， Germany， May 11–15， 1997 Proceedings 16. Springer Berlin Heidelberg， 1997： 256-266.

[37] Maurer U. Abstract models of computation in cryptography[C] //Cryptography and Coding： 10th IMA International Conference， Cirencester， UK， December 19-21， 2005. Proceedings 10. Springer Berlin Heidelberg， 2005： 1-12.

[38] Ben-Sasson E， Chiesa A， Green M， et al. Secure sampling of public parameters for succinct zero knowledge proofs[C]//2015 IEEE Symposium on Security and Privacy. IEEE， 2015： 287-304.

[39] Bowe S， Gabizon A， Miers I. Scalable multi-party computation for zk-SNARK parameters in the random beacon model[J]. Cryptology ePrint Archive， 2017.

[40] Groth J， Kohlweiss M， Maller M， et al. Updatable and universal common reference strings with applications to zk-SNARKs[C] //Annual International Cryptology Conference. Cham： Springer International Publishing， 2018： 698-728.

[41] Maller M， Bowe S， Kohlweiss M， et al. Sonic： Zero-knowledge SNARKs from linear-size universal and updatable structured reference strings[C]//Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security. 2019： 2111-2128.

[42] Gabizon A， Williamson Z J， Ciobotaru O. Plonk： Permutations over lagrange-bases for oecumenical noninteractive arguments of knowledge[J]. Cryptology ePrint Archive， 2019.

[43] https：//github.com/AztecProtocol

[44] Schwartz J T. Fast probabilistic algorithms for verification of polynomial identities[J]. Journal of the ACM （JACM）， 1980， 27（4）： 701-717.

[45] Bootle J， Cerulli A， Chaidos P， et al. Efficient zero-knowledge arguments for arithmetic circuits in the discrete log setting[C] //Advances in Cryptology–EUROCRYPT 2016： 35th Annual International Conference on the Theory and Applications of Cryptographic Techniques， Vienna， Austria， May 8-12， 2016， Proceedings， Part II 35. Springer Berlin Heidelberg， 2016： 327-357.

[46] Bootle J， Cerulli A， Chaidos P， et al. Efficient zero-knowledge arguments for arithmetic circuits in the discrete log setting[C]// Advances in Cryptology-EUROCRYPT 2016： 35th Annual International Conference on the Theory and Applications of Cryptographic Techniques， Vienna， Austria， May 8-12， 2016， Proceedings， Part II 35. Springer Berlin Heidelberg， 2016： 327-357.

[47] Hoffmann M， Kloo? M， Rupp A. Efficient zero-knowledge arguments in the discrete log setting， revisited[C]//Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security. 2019： 2093-2110.

[48] Daza V， Ràfols C， Zacharakis A. Updateable inner product argument with logarithmic verifier and applications[C]//Public-Key Cryptography- PKC 2020： 23rd IACR International Conference on Practice and Theory of Public-Key Cryptography， Edinburgh， UK， May 4–7， 2020， Proceedings， Part I 23. Springer International Publishing， 2020： 527-557.

[49] 宋英齊，馮榮權.零知識證明在區塊鏈中的應用綜述[J].廣州大學學報（自然科學版），2022，21（04）：21-36.

[50] https：//www.getmonero.org/

[51] https：//github.com/scroll-tech

[52] https：//github.com/starknet-io

[53] https：//github.com/taikoxyz

[54] https：//github.com/succinctlabs

[55] https：//github.com/Electron-Labs

[56] https：//www.zkibc.com/

[57] https：//github.com/topics/polyhedra

[58] https：//zkbridge.com/

[59] Setty S. Spartan： Efficient and general-purpose zkSNARKs without trusted setup[C]//Annual International Cryptology Conference. Cham： Springer International Publishing， 2020： 704-737.

[60] Xie T， Zhang Y， Song D. Orion： Zero knowledge proof with linear prover time[C]//Annual International Cryptology Conference. Cham： Springer Nature Switzerland， 2022： 299-328.

[61] Yang K， Sarkar P， Weng C， et al. Quicksilver： Efficient and affordable zero-knowledge proofs for circuits and polynomials over any field[C]//Proceedings of the 2021 ACM SIGSAC Conference on Computer and Communications Security. 2021： 2986-3001.

[62] Lyubashevsky V， Nguyen N K， Plan?on M. Lattice-based zero- knowledge proofs and applications： shorter， simpler， and more general[C]//Annual International Cryptology Conference. Cham： Springer Nature Switzerland， 2022： 71-101.

[63] Lu T， Wei C， Yu R， et al. Cuzk： Accelerating zero-knowledge proof with a faster parallel multi-scalar multiplication algorithm on gpus[J]. Cryptology ePrint Archive， 2022.

引用格式：萬巍，劉建偉，龍春，李婧，楊帆，付豫豪，袁梓萌.區塊鏈上的零知識證明技術及其典型算法、工具綜述[J].農業大數據學報，2024，6（2）：205-219. DOI： 10.19788/j.issn.2096-6369.200002.

CITATION： WAN Wei， LIU JianWei， LONG Chun， LI Jing， YANG Fan， FU YuHao， YUAN ZiMeng. An Overview of Zero-Knowledge Proof Technology and Its Typical Algorithms and Tools[J]. Journal of Agricultural Big Data， 2024，6（2）：205-219. DOI： 10.19788/j.issn.2096-6369.200002.

An Overview of Zero-Knowledge Proof Technology and Its Typical Algorithms and Tools

WAN Wei1，2， LIU JianWei1，2， LONG Chun1，2*， LI Jing1， YANG Fan1， FU YuHao1， YUAN ZiMeng1，2

1. Computer Network Information Center， Chinese Academy of Sciences， Beijing 100083， China;2. University of Chinese Academy of Sciences， Beijing 100049， China

Abstract： In the context of the increasing importance of data security and privacy protection， Zero-Knowledge Proofs （ZKPs） have provided a powerful tool for protecting privacy. This article comprehensively discusses the technology of zero-knowledge proofs and their application in modern cryptography. First， the article introduces the basic concepts of zero-knowledge proofs， as well as different types of ZKPs such as Snarks and Starks， along with their technical characteristics and application scenarios. In particular， the article conducts an in-depth study of ZK-Snarks. At the same time， the article also discusses other proof mechanisms such as ZK-Stark and Bulletproofs， comparing their differences in design and performance. Then， it focuses on the application of ZKPs in the blockchain environment and analyzes the related tools for writing zero-knowledge proofs. Finally， it points out some potential problems and future research directions in the field of zero-knowledge proofs.

Keywords： zero-knowledge proof; privacy protection; blockchain applications