生活中常見的圓周運動問題分類剖析

【摘要】高中物理中圓周運動可以根據不同情境和狀態總結出各種模型，也有對應的命題特點和解題思路.生活中常見的圓周運動模型主要有三類：轉彎模型、拱橋模型、轉盤模型，總結問題特點和解題思路，有助于學生更高效地分析問題，解決問題.

【關鍵詞】高中物理；圓周運動；解題技巧

1轉彎模型

轉彎模型主要有兩大考查方向：一是火車轉彎做圓周運動，二是圓弧路段汽車做圓周運動.轉彎模型的分析與解答，應結合受力分析和向心力的來源求解.

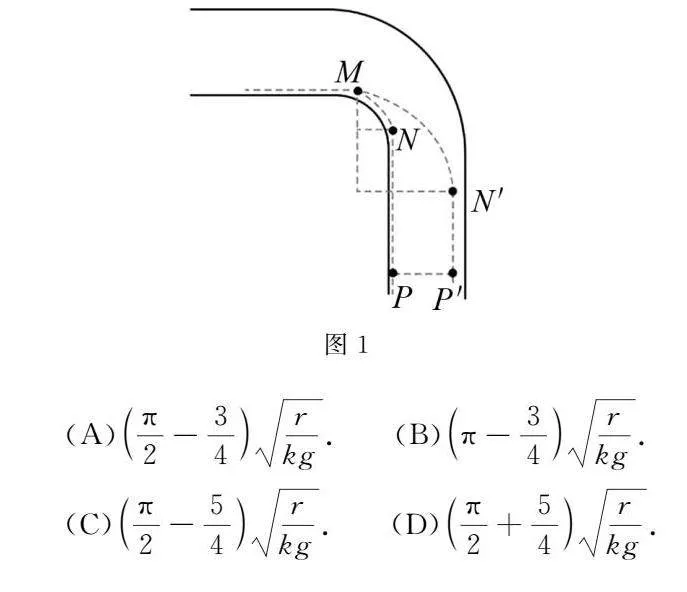
例1如圖1所示，MN為半徑為r的14圓弧路線，NP為長度為19r的直線路線，MN′為半徑為4r的14圓弧路線，N′P′為長度為16r的直線路線.賽車從M點以最大安全速度通過圓弧路段后立即以最大加速度沿直線加速至最大速度vm，并保持vm勻速行駛.已知賽車勻速轉彎時徑向最大靜摩擦力和加速時的最大合外力均為車重的k倍，最大速度vm=6kgr，g為重力加速度，賽車從M點按照路線MNP運動到P點與按照MN′P′路線運動到P′的時間差為（）

（A）π2－34rkg. （B）π－34rkg.

（C）π2－54rkg. （D）π2+54rkg.

分析分別對兩種不同軌道MNP和MN′P′進行分析，賽車在軌道上的運動由圓周運動和直線運動組合形成，在圓弧軌道上由外力提供向心力，產生向心加速度，聯合不同公式表示運動時間，通過運算求出時間差.

解賽車從M點按照MNP路線運動到P點過程中做勻速圓周運動通過有kmg=mv21MAPsOMgEuiiZB0kL11AlkA==r，

t1=T14=14·2πrv1，

在NP直線路線上做勻加速直線運動，有kmg=ma1，

vm=v1+a1t2，

解得t1=πkgr2kg，t2=5kgrkg，

可知在NP直線路線勻加速至最大速度過程的位移為

x1=v1+vm2t2=17.5r＜19r，

則勻速運動過程的時間為t3=19r－x1vm=kgr4kg；

賽車從M點按照MN′P′路線運動到P′點過程中做勻速圓周運動，有kmg=mv224r，

t4=T24=14·2π·4rv2，

在N′P′直線路線上做勻加速直線運動，有kmg=ma2，

vm=v2+a2t5，

解得t4=πkgrkg，t5=4kgrkg，

可知在N′P′直線路線勻加速至最大速度過程的位移為x2=v2+vm2t5=16r，

勻加速至最大速度時，恰好到達P′，則賽車從M點按照MNP路線運動到P點與按照MN′P′路線運動到P′點的時間差為Δt=t4+t5－t1－t2－t3，

可知Δt=π2－54rkg，正確答案為選項（C）.

2拱橋模型

拱橋模型中，可將拱橋類比成圓周運動的一部分軌道，這類模型的解題思路主要在最高點物體所受重力和橋面對物體的支持力的合力提供向心力.這類模型還可以拓展成豎直平面的凹槽圓弧軌道運動，分析思路都比較相似，需要認真分析與解讀.

例2當汽車通過拱橋頂點的速度為v時，車對橋頂的壓力為車重的34，如果要使汽車安全通過該拱橋（不脫離地面），則汽車通過橋頂的速度可以為（）

（A）v2. （B）v3. （C）3v. （D）4v.

分析首先分析最高點位置提供向心力的合力組成部分，其次分析汽車做圓周運動臨界狀態需要提供的合力大小，最后分析安全速度與原速度的關系，可得到答案.

解根據牛頓第三定律，

可得FN=34mg，

根據牛頓第二定律，

可得mg－FN=mv2r，

mg=mv′2r，

解得v′=2v，

汽車速度小于2v時，能安全通過該拱橋（不脫離地面），故正確答案為選項（A）（B）.

3轉盤模型

轉盤模型中，物體做圓周運動的向心力主要由摩擦力提供，其他特殊情況還需要特別分析.分析和解答轉盤模型，應結合角速度ω、向心力合外力F列式求解.

例3如圖3所示，在勻速轉動的水平圓盤上，沿直徑方向放著用輕繩相連可視為質點的物體A和物體B，A的質量為3m，B的質量為m，它們分居圓心兩側，到圓心的距離分別為RA=r，RB=2r，A、B與盤間的動摩擦因數相同，最大靜摩擦力等于滑動摩擦力.A、B與圓盤一起繞中軸線勻速轉動的最大角速度為ω1；若只將B的質量增加為2m，A、B與圓盤一起繞中軸線勻速轉動的最大角速度為ω2.轉動過程中輕繩未斷，則ω1ω2為.

分析首先分析不同物體在同一水平面上以不同角速度做圓周運動的具體情況，其中向心力由繩子拉力和摩擦力的合力構成，需要列式求解，用變量表示并得到具體答案.

解當A、B與圓盤一起繞中軸線勻速轉動達到最大角速度ω1時，

對B：T－μmg=mω21·2r，

對A：T+μ·3mg=3mω21r，

解得ω1=2μgr，

若只將B的質量增加為2m，A、B與圓盤一起繞中軸線勻速轉動的最大角速度為ω2時，

對B：T′+μ·2mg=2mω22·2r，

對A：T′－μ·3mg=3mω22r，

解得ω2=5μgr，

所以ω1ω2=25.

4結語

上文列舉了3種常見的圓周運動模型，不同模型的特點和對應解題思路都是學生需要掌握的內容.解答圓周運動問題的要點是找到提供向心力的合外力，還需要結合牛頓運動定律、動能定理進行求解.

參考文獻：

［1］毛寧，吳峰，惠治鑫，等.基于"圓周運動"模型建構的高中物理深度學習[J].物理通報，2022（08）：63-67+73.

［2］鮑龍.高中物理模型的分類及建模重要性[J].中學生數理化（教與學），2017（04）：20.