非線性關系在高中物理中的分析策略

【摘要】本文通過對高中物理中常見的非線性關系進行分析，結合具體實例闡述解決非線性問題的方法．旨在幫助高中學生更好地理解和掌握非線性關系的解決策略，提高解決物理問題的能力．

【關鍵詞】高中物理；非線性關系；解題方法

在高中物理的學習中，學生常常會遇到各種線性關系和非線性關系．線性關系相對簡單，其規律易于理解和掌握．然而，非線性關系是指兩個物理量之間的關系不是簡單的正比關系，不能用一次函數來表示，往往需要運用特定的分析策略才能有效地解決問題．

1 運動學中非線性關系的處理方法

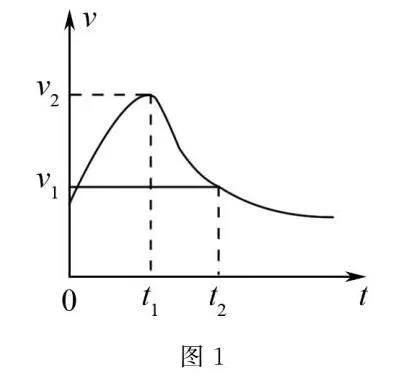
例1貴州省是全國唯一沒有平原的省份，現已實現縣縣通高速．現一輛轎車正在一段平直的鄉村公路上行駛，其速度隨時間變化的圖象如圖1所示，則下列說法正確的是（）

（A）在0～t1時間內轎車做勻變速運動．

（B）在t1～t2時間內轎車的平均速度小于v1+v22．

（C）在t1時刻轎車的加速度達到最大值．

（D）在t2時刻轎車的加速度和速度方向相同．

解析由v－t圖象的斜率表示加速度可知，在0～t1時間內，圖象的斜率逐漸減小，則轎車的加速度逐漸減小，做加速度逐漸減小的加速運動，（A）錯誤；由v－t圖象與橫坐標軸所圍面積表示位移可知，在t1～t2時間內轎車的位移小于x=v1+v22t2－t1，因此在t1～t2時間內轎車的平均速度小于v1+v22，（B）正確；由v－t圖象的斜率表示加速度可知，在t1時刻轎車的加速度達到最小值，是零，（C）錯誤；由v－t圖象的斜率表示加速度可知，在t2時刻圖象斜率是負值，因此轎車的加速度是負值，在t2時刻速度值在時間軸以上，是正值，因此在t2時刻加速度和速度方向相反，（D）錯誤．

評析高中階段的學生學習勻變速直線運動較多，對非勻變速直線運動解題經驗不足．如果v－t圖象不是傾斜直線，依然可根據v－t圖象的斜率表示加速度來進行求解．本題中，v與t沒有線性關系，但可根據斜率判斷加速度的大小和方向．

2動力學中非線性關系的處理方法

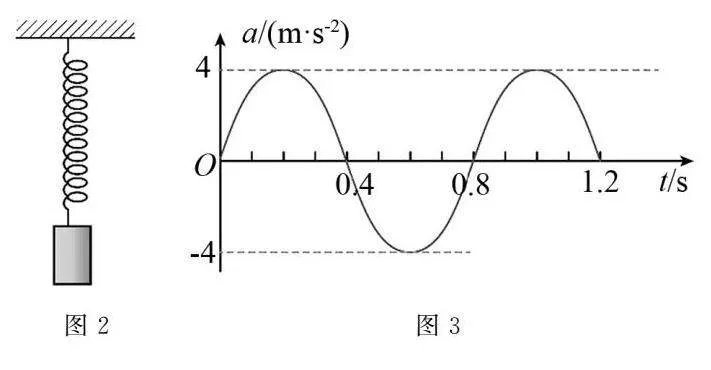
例2圖2為用手機和輕彈簧制作的振動裝置．手機加速度傳感器記錄了手機在豎直方向的振動情況，以向上為正方向，得到手機振動過程中加速度a隨時間t變化的曲線為正弦曲線，如圖3所示．下列說法正確的是（）

（A）t=0時，彈簧處于原長．

（B）t=0.2s時，手機位于平衡位置上方．

（C）從t=0至t=0.2s，手機的動能減小．

（D）a隨t變化的關系式為a=4sin（2.5πt）m/s2．

解析由圖3知，t=0時，手機加速度為0，由牛頓第二定律得彈簧彈力大小為F=mg，故（A）錯誤；由圖3知，t=0.2s時，手機的加速度為正，則手機位于平衡位置下方，故（B）錯誤；由圖3知，從t=0至t=0.2s，手機的加速度增大，手機從平衡位置向最大位移處運動，速度減小，動能減小，故（C）正確；由圖3知T=0.8s，則角速度ω=2πT=2.5πrad/s，則a隨t變化的關系式為a=4sin2.5πtm/s2，故（D）正確．

評析從圖象中可以看出，加速度a與時間t之間不是簡單的線性關系，但加速度的變化是周期性的，可根據加速度的變化情況，運用牛頓第二定律判斷力的變化情況，然后進行求解．本題中，根據圖象可得a隨t變化的關系式為a=4sin2.5πtm/s2，可知不同時刻手機的加速度．

3電學中非線性關系的處理方法

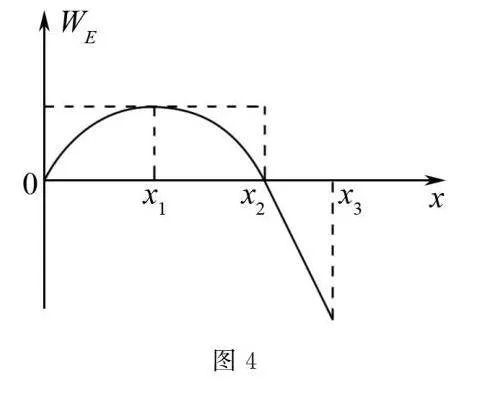
例3一帶負電粒子在僅受電場力作用下，從x=0的位置沿x軸正方向運動，電場力做功WE隨位移x的關系如圖4所示，其中x1為0～x2距離的中點，0～x2段的圖象是曲線，x2～x3段的圖象是直線，在0～x3過程中下列說法正確的是（）

（A）x1處的場強一定不為零．

（B）粒子在x1處電勢能最小．

（C）粒子從x2處運動到x3處過程中，電勢能不變．

（D）x1、x2、x3處的電勢φ1、φ2、φ3的關系為φ1<φ2<φ3．

解析圖4為一帶負電粒子在僅受電場力作用下的WE－x圖象，由WE=F·Δx可知，該圖象的斜率為帶電粒子所受的電場力，在x1處粒子所受的電場力為零，此處電場強度為零，（A）錯誤；粒子在0～x1過程，電場力做正功，電勢能減小，粒子在x1～x2過程，電場力做負功，電勢能增加，粒子在x1處電勢能最小，（B）正確； 粒子在x2～x3過程，電場力做負功，電勢能增加，（C）錯誤；在0～x1過程，電場對粒子做正功，在x1～x3過程，圖象的斜率方向反向，即粒子所受電場力的方向反向，電場力做負功，電勢能增加，粒子在x2處電勢能大于x1處的電勢能，由于粒子帶負電，所以電勢能大的地方，其電勢小，即φ1>φ2，在x2～x3過程，同理可得φ2>φ3，綜上所述有φ1>φ2>φ3，（D）錯誤．

評析WE－x圖象對高中學生而言比較陌生，由WE=F·Δx可知，圖象的斜率表示帶電粒子所受的電場力，盡管WE與x之間沒有線性關系，但可根據圖象的走勢判斷電場力的變化，再根據電場力做功判斷電勢能和電勢．

4結語

非線性關系在高中物理中廣泛存在，對于學生理解物理現象、提高物理思維能力具有重要意義．在分析非線性關系時，可以從不同角度入手，深入理解物理量之間的變化規律．通過對高中物理中常見的非線性關系現象進行分析和實例計算，可以更好地掌握這些分析策略的應用方法，提高解決物理問題的能力．

參考文獻：

[1]魯移林，柯云霞.轉化和換元方法在高中物理非線性類問題中的應用[J].教學考試，2023（13）：52-54.