基于機器學習的螺栓連接接觸狀態實時預測

摘要：螺栓連接系統界面間的接觸狀態是衡量其工作狀態和密封性能的重要指標。由于受到較強接觸非線性和過多耦合變量的影響，接觸應力分布的實時預測依然是一個難題。借助機器學習的方法，將復雜的螺栓連接問題封裝在后臺運算里，最終呈現出一個簡單的能夠實時預測接觸應力分布的前臺操作。

關鍵詞：螺栓連接；接觸應力；機器學習；實時預測

中圖分類號：TH131文獻標志碼：A文章編號：1671-5276（2024）06-0032-05

Abstract：The contact status of bolted joint between system interfaces is an important indicator measuring its working condition and sealing performance， the real-time prediction of contact stress distribution， however， remains a challenge due to the effects from strong contact nonlinearity and exceeding coupling variables. This article， with the help of machine learning technique， presents a simple front operation window capable of predicting the contact stress distribution in real-time by packaging the complicated bolted joints into background computational process.

Keywords：bolted joints; contact stress; machine learning; real-time prediction

0引言

螺栓作為工業裝備中常見的連接單元被大量運用，緊固件間的接觸情況一直是領域內的熱點和難點。CHANDRASHEKHARA等［1］解析研究發現有孔的板在軸對稱載荷作用下，板內法向應力的分布只和兩個無量綱參數（受載區域徑向尺寸與板厚度的比值、孔半徑與板厚度的比值）相關，與板的材料屬性和外載荷強度無關，該結論廣泛地被螺栓研究所采用［2-3］。MA等［4］通過有限元仿真系統地分析了螺栓連接接觸壓力的分布情況，發現螺母與被緊固件之間的靜摩擦力也對接觸區域起著決定性作用，而這恰恰是被大家所忽視的。上述學者的研究基本明確了影響螺栓連接系統接觸狀態的主要因素。

實時接觸狀態的預測，依然是相關行業所夢寐以求的，它可以極大地提高螺栓連接結構、大幅度地縮短整機的研發周期。但是，正如前文所述，螺栓連接結構具有較強的接觸非線性和過多變量參數，所以想要從數學上建立起接觸應力分布與影響因素之間的顯式映射關系是非常困難的。另一方面，得益于人工智能技術的飛速發展，機器學習已經成為了一種捕捉輸入和輸出數據之間映射關系的強有力工具［5-6］。實際上，近期已經有一些學者將機器學習技術運用到螺栓連接中，解決了一些難題［7-8］。雖然上述這些工作充分驗證了人工智能和螺栓連接研究相結合的優點，但更多的是將人工智能技術應用在螺栓連接結構工作狀態的監測上，而不是在更加前端的產品研發設計階段。

本文的研究工作是將人工智能技術用在螺栓連接結構的研發設計階段，借助于機器學習的方法，將復雜的螺栓連接問題封裝在后臺運算里，最終呈現出一個簡單的能夠實時預測接觸應力分布的前臺操作。為了達到這個目的，首先基于數值分析結果對接觸應力分布的主要影響因素進行了降維，極大地減小了所需的樣本數量。隨后，通過二維軸對稱有限元模型生成了較大規模的訓練集，并利用4種機器學習模型（支持向量回歸、K最近鄰回歸、多項式回歸和神經網絡回歸）建立起接觸應力分布和影響因素之間的映射關系。最后通過3次相互獨立的測試表明本文所提出的實時預測模型具有較高的精度。

1問題描述

本章首先提出一種基于物理和數值分析的接觸應力分布尺寸rmax的影響因素降維方法，隨后，給出rmax基于機器學習模型的數學表征。

1.1接觸應力影響因素的降維

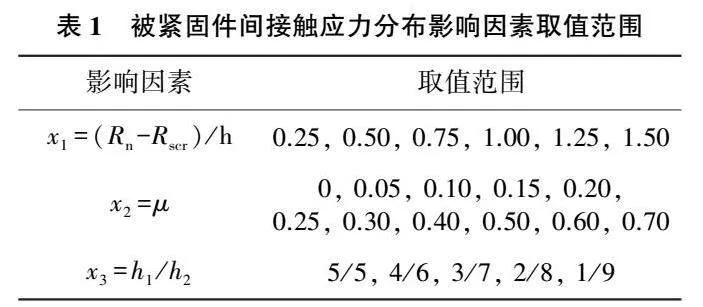
對于圖1所示的螺栓連接結構，根據前文所述可以知道，兩個無量綱的幾何參數和螺母與被緊固件之間的摩擦因數都顯著影響rmax的數值，即這里對應Rn/h、Rscr/h和μ，其中Rn和Rscr分別為螺母和螺桿的半徑。因為螺母的半徑可以近似認為是螺桿或螺栓孔的1.5倍［9-12］，所以上述的兩個無量綱的幾何參數對于螺栓連接來說，可以等效為一個［13］。此外，還可以肯定的是，兩個不同厚度的被緊固件也會影響接觸應力分布的范圍。因此總的來說，圖1所示的螺栓連接問題，共有3個因素影響rmax的數值，即

式中：h1和h2分別為兩個被緊固件的厚度；h為被緊固件總厚度的一半，滿足下式：

至此便完成了rmax影響因素基于物理和數值分析的降維過程。

1.2螺栓連接機器學習模型的數學表征

綜上所示，可以看出rmax和x之間存在著一個真實的映射關系f（·）：

但是，上述映射關系難以解析地表達。為了借助人工智能技術解決這個難題，首先可以獲得一組滿足式（3）的樣本集合T={（x1，r1max），…，（xn，rnmax）}。T可以合理地劃分為訓練集T1={（x1，r1max），…，（xm，rmmax）}和測試集T2={（xm+1，rm+1max），…，（xn，rnmax）}這兩個部分。通過采用合適的回歸分析模型對訓練集T1進行學習，便可以得到映射關系f∧（·）

而學習到的映射關系f∧（·）與真實映射關系f（·）之間的偏差，可以通過測試集T2進行度量，方均根誤差RMSE定義為

本文將采用4種回歸分析模型，即支持向量回歸（SVR）、K最近鄰回歸（KNN）、多項式回歸（PR）和多層感知器回歸（MLP），對該螺栓連接問題進行分析。這4種回歸模型的數學表征如下。

1）支持向量回歸

支持向量回歸是希望基于訓練集T1在樣本空間中找到一個如式（6）所示的超平面模型

使得預測值r∧max和真實值rmax盡可能接近。其中w=（w1，w2，…，wd）為法向量，決定了超平面的方向；b是位移項，決定了超平面與原點之間的距離。SVR回歸具體的解析推導過程這里不再給出，讀者可以參考文獻。

2）K最近鄰回歸

KNN回歸是通過求解與要預測的點x距離最近的k個鄰居xi，然后對這k個鄰居的值做平均后得到的。為了提高預測的精度，也可以對不同距離的鄰居對要預測的點產生的影響賦予不同的權值wi，使距離近的鄰居的值對回歸的貢獻更大。KNN回歸模型可以寫為

式中d（·）為距離度量函數。

3）多項式回歸

滿足多項式回歸的映射關系可以寫為

式中bi是需要通過訓練集T1確定的模型參數。此外，需要強調的是，在進行回歸分析的時候，可以在上式中截取所需要的某次冪的特征項來保證預測的精度。

4）神經網絡回歸

多層感知器是神經網絡最常用的類型，它是由1個輸入層、1個或多個隱藏層和1個輸出層組成的前饋網絡。對于本文研究的問題，MLP模型可以表示為下式［14］：

式中：alj是第l層中第j個神經元的值；wlij是神經元al-1i到神經元alj之間的連接權重。

2數值算例

首先，采用二維軸對稱有限元模型獲取機器學習所需的數據樣本。隨后，采用4種回歸模型分別對上述數據樣本進行學習和預測。

2.1樣本獲取

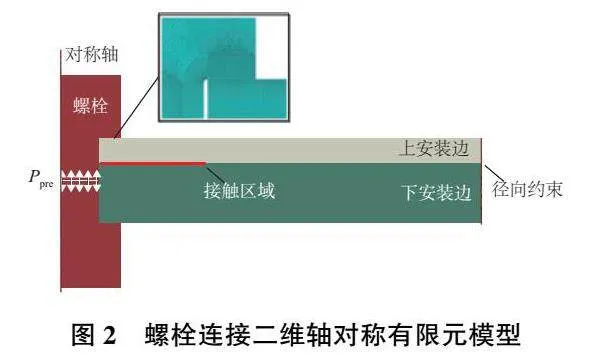
為了獲取樣本數據，采用有限元軟件建立起如圖2所示的螺栓連接二維軸對稱有限元模型。為了減小邊界效應對仿真精度的影響，算例將被緊固件徑向方向尺寸進行了加長處理，并施加了徑向位移約束。為了能夠精確地獲得被緊固件間接觸壓力的分布特征，在發生接觸的地方進行了網格密化。螺栓與被緊固件均采用高強度合金鋼材料，彈性模量為200GPa。

正如前文所述，被緊固件間接觸應力分布范圍rmax只與式（1）所述的3個影響因素密切相關，不依賴于螺栓的預緊力數值，這里螺栓的預緊力定義為P0=500MPa。通過將接觸應力分布的影響因素x=（x1，x2，x3）在其合理的取值區間內離散化后（表1），利用如圖2所示的有限元模型最終得到了共計330個數據樣本。

2.2機器學習

1）單螺栓連接

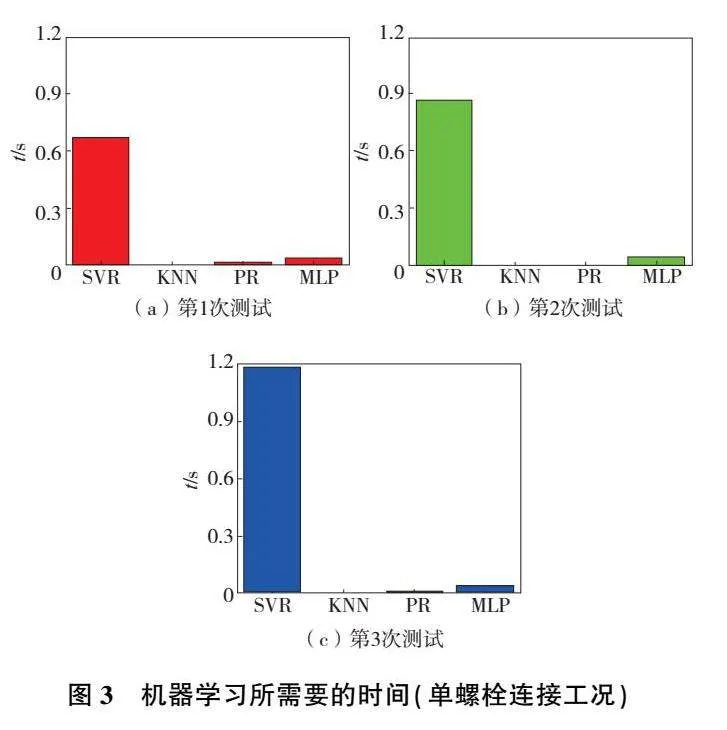
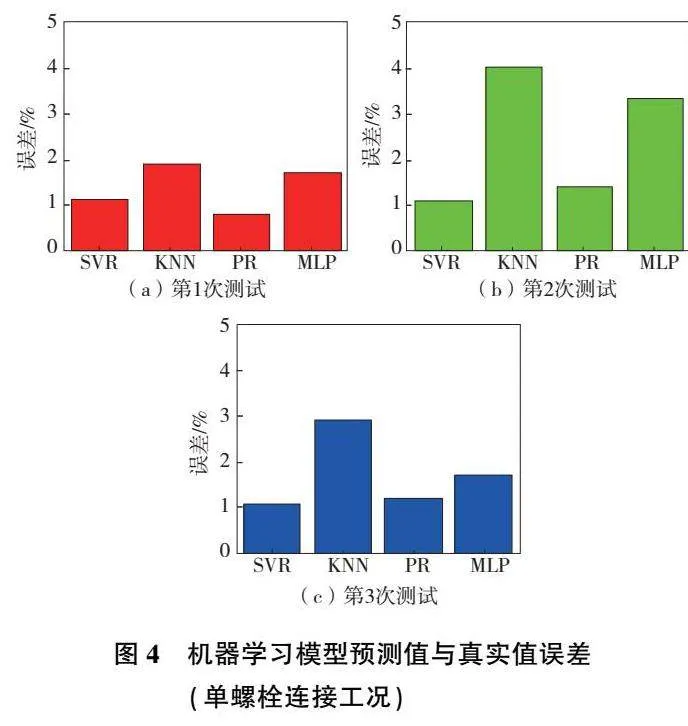
這里將330組數據樣本隨機分為兩組：由320個樣本構成的訓練集T1和由10個樣本組成的測試集T2。在進行了3次相互獨立的上述分組后，分別采用4種回歸模型（SVR、KNN、PR和MLP）對訓練集進行了學習，學習所需時間如圖3所示。可以看出，這4種回歸模型學習所用時間都較為短暫，時間最長的SVR模型用時也不超過1.2s；而KNN和PR所用時間最短，基本在毫秒級。隨后，上述4種回歸模型學習得到的映射關系通過測試集T2來進行檢驗，它們預測的接觸區域尺寸與真實值之間的方均根誤差RMSE如圖4所示。可以看出，這4種回歸模型都表現出了較高的精度，最大誤差不超過4%。其中，KNN和MLP誤差相對較大，最大分別能達到4%和3.4%，而SVR和PR誤差相對較低，誤差最大值均不超過1.5%。

2）多螺栓緊密連接

當多螺栓緊密連接時，例如航空發動機薄壁機匣的螺栓連接結構，不同測量方向，被緊固件間接觸壓力分布的情況是不一樣的。測量路徑如果沿著垂直于螺栓排布的方向，就會發現相鄰螺栓壓應力之間的耦合作用可以忽略。此時，壓應力分布和單個螺栓預緊下沒有明顯的區別（上節單個螺栓連接的機器學習結果依然適用）；而沿著螺栓排布方向測量，接觸壓力分布的耦合作用最大，此時被緊固件間接觸壓力的分布等同于一個同樣厚度的厚板在相同位置的法向應力［15］。

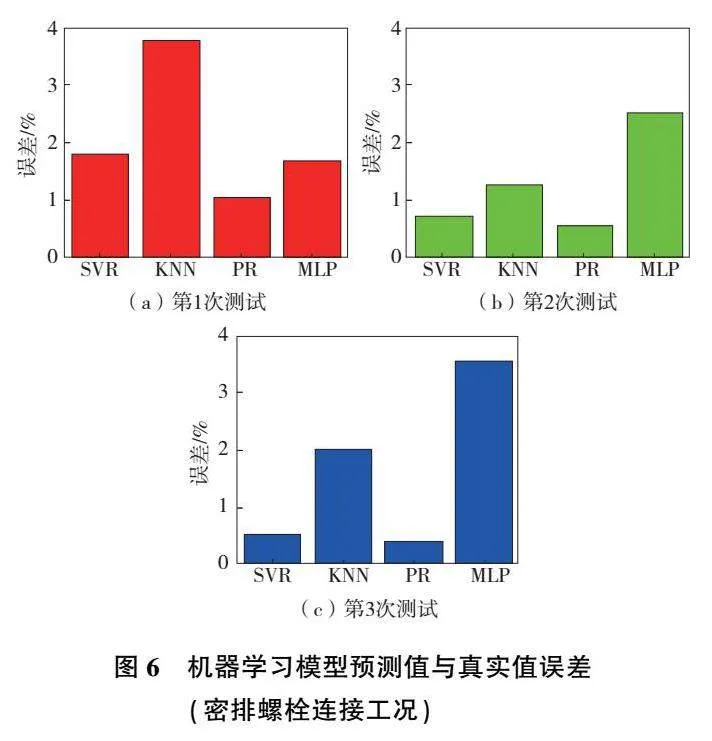
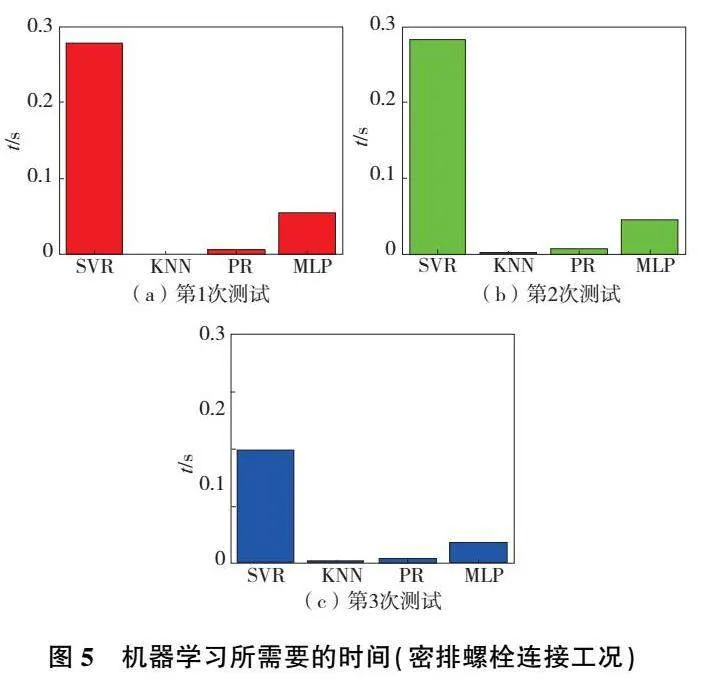
因此，為了能夠實時預測多個密排螺栓連接下沿著螺栓排布方向接觸壓力分布的特點，可以通過將圖2所示有限元模型中的兩個被緊固件合為一個整體，測量結合處的法向應力，最終獲得330組數據樣本。這330組數據樣本依然可以隨機分為兩組：由320個樣本構成的訓練集T1和由10個樣本組成的測試集T2。在進行3次相互獨立的上述分組后，分別采用4種回歸模型對訓練集進行學習，學習所需時間如圖5所示。可以看出，SVR模型用時依然是最長的，最大可達0.28s。其他3種方法用時都較短，最短的KNN模型，最大用時0.98ms。隨后，上述4種回歸模型學習得到的映射關系將通過測試集T2來進行檢驗，它們預測的接觸區域尺寸與真實值之間的方均根誤差RMSE如圖6所示。可以看出，這4種模型都表現出了較高的精度，最大誤差不超過4%。其中，SVR和PR誤差一直相對較低，誤差最大值均不超過1.8%。

綜上分析，可以看出針對本文研究的螺栓連接問題，上述這4種回歸模型都可以呈現出一個穩定的、精確的預測結果。因此，通過基于物理和數值分析的影響因素降維處理后，借助于機器學習的方法，完全可以實現將該復雜的螺栓連接問題封裝在后臺運算里，只給用戶呈現出一個簡單的能夠實時地預測接觸應力分布的前臺操作。

3結語

本文提出了一個能夠實時預測螺栓連接系統被緊固件間接觸應力分布的模型。它是通過利用機器學習的方式將復雜的螺栓連接問題封裝在后臺運算里，呈現出一個較為簡單的前臺操作來實現的。本文基于物理和數值分析的結果，對應力分布影響因素進行了降維處理，大大減小了所需樣本的數目，并進一步采用有限元法獲取了大量的數據樣本。隨后，采用了4種機器學習模型來尋找接觸應力分布和影響因素之間的映射關系，這4種模型都呈現出了較高的精確性。本文所提的實時預測方法也可以推廣到其他工況，比如考慮內氣壓作用。此外，因為螺栓連接還存在著很多研究難點，比如疲勞預測等。因此本文所提出的機器學習方法也有解決這些難題的潛能。

參考文獻：

［1］ CHANDRASHEKHARA K，MUTHANNA S K. Stresses in a thick plate with a circular hole under axisymmetric loading［J］. International Journal of Engineering Science，1977，15（2）：135-146.

［2］ PAU M，BALDI A. Application of an ultrasonic technique to assess contact performance of bolted joints［J］. Journal of Pressure Vessel Technology，2007，129（1）：175-185.

［3］ STEPHEN J T，MARSHALL M B，LEWIS R. An investigation into contact pressure distribution in bolted joints［J］. Proceedings of the Institution of Mechanical Engineers，Part C：Journal of Mechanical Engineering Science，2014，228（18）：3405-3418.

［4］ MA B B，ZHU Y C，JIN F，et al. A lightweight optimal design model for bolted flange joints without gaskets considering its sealing performance［J］. Proceedings of the Institution of Mechanical Engineers，Part E：Journal of Process Mechanical Engineering，2018，232（2）：234-255.

［5］ 李航. 統計學習方法［M］. 北京：清華大學出版社，2012.

［6］ 周志華. 機器學習［M］. 北京：清華大學出版社，2016.

［7］ CATBAS F N，MALEKZADEH M. A machine learning-based algorithm for processing massive data collected from the mechanical components of movable bridges［J］. Automation in Construction，2016，72：269-278.

［8］ CHA Y J，YOU K，CHOI W. Vision-based detection of loosened bolts using the Hough transform and support vector machines［J］. Automation in Construction，2016，71：181-188.

［9］YANG G Q，HONG J，WANG N，et al. Member stiffnesses and interface contact characteristics of bolted joints［C］//2011 IEEE International Symposium on Assembly and Manufacturing （ISAM）. Tampere，Finland： IEEE，2011：1-6.

［10］ SETHURAMAN R，SASI KUMAR T. Finite element based member stiffness evaluation of axisymmetric bolted joints［J］. Journal of Mechanical Design，2009，131（1）：1-5.

［11］ PEDERSEN N L，PEDERSEN P. Stiffness analysis and improvement of bolt-plate contact assemblies#［J］. Mechanics Based Design of Structures and Machines，2008，36（1）：47-66.

［12］ NASSAR S A，ABBOUD A. An improved stiffness model for bolted joints［J］. Journal of Mechanical Design，2009，131（12）：1.

［13］ MA B B，JIN F，SUN Z，et al. Leakage analysis of bolted flange joints considering surface roughness：a theoretical model［J］. Proceedings of the Institution of Mechanical Engineers，Part E：Journal of Process Mechanical Engineering，2018，232（2）：203-233.

［14］YANG H，GUO X，TANG S，et al. Derivation of heterogeneous material laws via data-driven principal component expansions［J］. Computational Mechanics，2019，64（2）：365-379.

［15］ 馬奔奔，朱一超，丁全，等. 無墊圈螺栓連接系統優化設計和泄漏率預測［J］. 強度與環境，2018，45（4）：38-46.

收稿日期：20230413

基金項目：中央高校研究基金項目（DUT20RC（3）020）；大連人才創新計劃項目（2020RQ099）

第一作者簡介：趙偉（1983—），男，四川眉山人，高級工程師，碩士，研究方向為風電機組結構動力學，zhaowei@dongfang.com。

DOI：10.19344/j.cnki.issn1671-5276.2024.06.006