基于PIV測試的徑向入流旋轉(zhuǎn)盤腔流動特性研究

摘要：將PIV技術(shù)應(yīng)用于壓氣機(jī)徑向入流的簡單盤腔中，使用實驗研究旋轉(zhuǎn)雷諾數(shù)和流量系數(shù)對于盤腔內(nèi)部旋流數(shù)以及流場的影響，得到入口旋流數(shù)Cin隨羅斯比數(shù)Ro變化以及非線性修正系數(shù)Ki隨湍流參數(shù)λ變化的擬合公式；提出OWEN等人模型的修正方法，使其可以更好地應(yīng)用于工程。研究發(fā)現(xiàn)：旋轉(zhuǎn)雷諾數(shù)的增大會導(dǎo)致旋流數(shù)變化趨勢減慢，使得整個流場實現(xiàn)更穩(wěn)定的分層；流量系數(shù)的增大會導(dǎo)致旋流數(shù)變化趨勢增快，同時會使流場中的粒子以更為規(guī)則的方式沿轉(zhuǎn)盤旋轉(zhuǎn)方向運(yùn)動。

關(guān)鍵詞：壓氣機(jī)；粒子圖像測速；旋轉(zhuǎn)盤腔；旋流數(shù)

中圖分類號：TH138文獻(xiàn)標(biāo)志碼：B文章編號：1671-5276（2024）06-0062-06

Abstract：By applying PIV technology to a simple disk cavity with radial inflow， studies the influence of rotating Reynolds number and flow coefficient on the swirl number and flow field in the disk cavity， obtaining the fitting formula of the inlet swirl number Cin with Ro and the nonlinear correction coefficient Ki. Thus an method for modifying the nonlinear model is proposed for better application in engineering. It is found that the increase of the rotating Reynolds number will lead to the decrease of the cyclone number， making the entire flow field achieve more stable stratification. And the increase of the flow coefficient will result in the increase of the cyclone number， and meanwhile make the particles in the flow field move in a more regular way along the rotation direction of the rotating disk.

Keywords：compressor; PIV; rotating disk cavity; number of swirls

0引言

壓氣機(jī)引氣作為空氣系統(tǒng)的源頭，其工作特性對冷卻空氣的品質(zhì)及對熱端部件的冷卻效果具有重要影響［1］。內(nèi)部引氣系統(tǒng)從兩級壓氣機(jī)盤間引氣，經(jīng)過兩個盤之間的鼓筒引氣孔徑向流向盤心，并經(jīng)盤間空腔向后或向前流出，這種形式的盤腔流動被國內(nèi)外研究學(xué)者稱為徑向進(jìn)氣旋轉(zhuǎn)盤腔。高速旋轉(zhuǎn)盤腔內(nèi)的流動復(fù)雜，影響因素眾多，阻礙著流體的徑向流動，導(dǎo)致徑向引氣過程中氣流壓力和引氣量急劇下降［2-3］。這一現(xiàn)象直接導(dǎo)致用于冷卻密封的空氣品質(zhì)降低，制約了發(fā)動機(jī)性能的提升。在實際應(yīng)用中有很多小型的發(fā)動機(jī)沒有充足的空間來安裝減渦器。在工程中對盤腔內(nèi)部的流動進(jìn)行正的預(yù)估是十分必要的。OWEN等［4］建立了自由渦模型和非線性模型來預(yù)估盤腔內(nèi)部的旋流數(shù)分布，在湍流參數(shù)λ為0.007～0.140的范圍內(nèi)具有很高的精度。但是由于圓盤附近非線性慣性和離心力與線性科里奧利力相比通常可以忽略不計的假設(shè)，導(dǎo)致在湍流參數(shù)λ大于0.2之后的精度下降。因此針對傳統(tǒng)簡單盤腔建立更準(zhǔn)確的預(yù)測模型非常有意義。

粒子圖像測速（particle image velocimetry，PIV）是獲取盤腔內(nèi)旋流數(shù)的有效試驗手段，國內(nèi)外學(xué)者［4-10］為進(jìn)一步研究盤腔內(nèi)部的流動細(xì)節(jié)，把流動可視化技術(shù)應(yīng)用在旋轉(zhuǎn)盤腔當(dāng)中來獲取內(nèi)部的流場結(jié)構(gòu)和速度場分布。本文將PIV技術(shù)應(yīng)用于徑向入流的旋轉(zhuǎn)盤腔當(dāng)中，重點分析轉(zhuǎn)速和流量對于盤腔內(nèi)的旋流數(shù)和正面速度云圖、正面實物圖的影響以及流量轉(zhuǎn)速之間對于旋流數(shù)的耦合影響。

1實驗設(shè)備以及測量手段

1.1試驗設(shè)備介紹

1）旋轉(zhuǎn)試驗臺

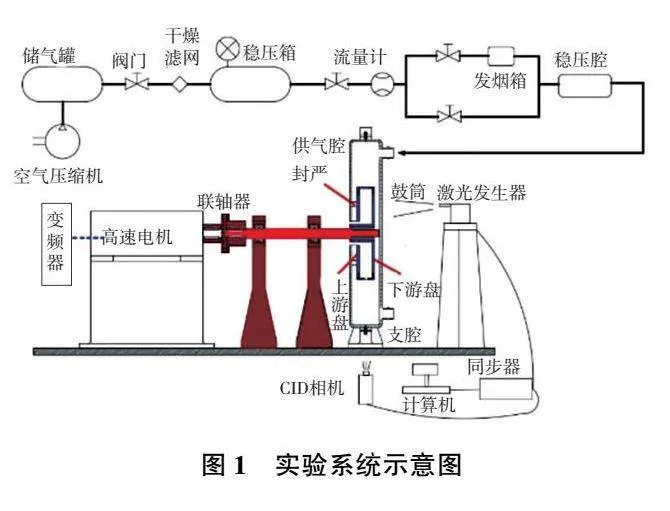
本文旋轉(zhuǎn)試驗臺如圖1所示，由旋轉(zhuǎn)盤腔和集齊腔、轉(zhuǎn)軸PIV拍攝系統(tǒng)、信號采集系統(tǒng)、供氣系統(tǒng)以及粒子供入系統(tǒng)所構(gòu)成。

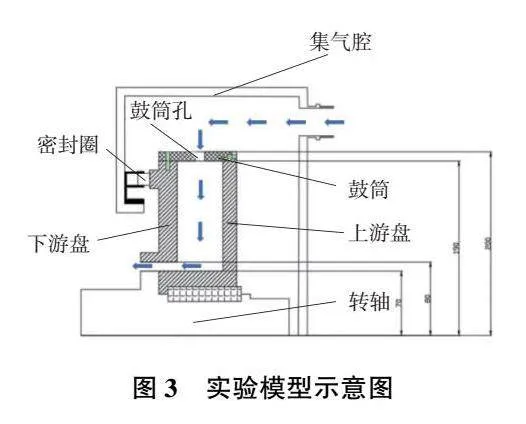
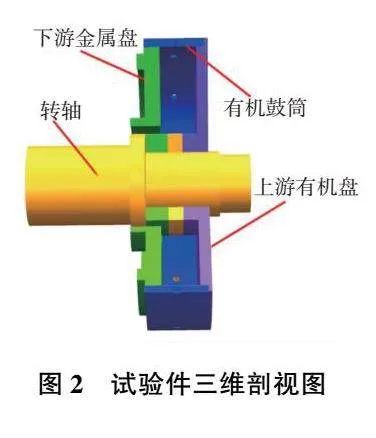
在該試驗段中，上游盤、下游盤和鼓筒圍成了旋轉(zhuǎn)盤腔，鼓筒上沿周向有均勻布置的鼓筒孔，位于盤腔的中間平面上。圖中金屬盤與有機(jī)盤之間的間距為50mm，進(jìn)氣孔的孔徑為10mm，個數(shù)為12個。圖2所示為本試驗中盤腔試驗件的剖視三維模型，圖3為旋轉(zhuǎn)試驗段的二維示意圖。

2）常規(guī)信號采集系統(tǒng)

本試驗需要常規(guī)的壓力、溫度以及流量的測試系統(tǒng)，用來測量集氣腔、供氣管路等靜止件內(nèi)的流場狀態(tài)。本試驗中信號采集裝置的名稱、量程與精度如表1所示。實驗操作臺如圖4所示。

圖4實驗操作臺

3）PIV拍攝系統(tǒng)

PIV測試設(shè)備硬件系統(tǒng)包括照明激光器、同步控制器、圖像采集板（放置于計算機(jī)內(nèi)）、高速數(shù)字相機(jī)和計算機(jī)。在流場中布撒大量示蹤粒子跟隨流場運(yùn)動把激光束經(jīng)過組合透鏡擴(kuò)束成片光照明流場，使用數(shù)字相機(jī)拍攝流場照片，得到前后兩幀粒子圖像。對圖像中的粒子圖像進(jìn)行互相關(guān)計算，得到流場一個切面內(nèi)定量的速度分布。PIV系統(tǒng)實物如圖5所示。

4）粒子發(fā)生系統(tǒng)

粒子發(fā)生系統(tǒng)由小型空氣壓縮機(jī)、粒子發(fā)生器、示蹤粒子組成。PIV系統(tǒng)中小型空氣壓縮機(jī)的作用是給粒子發(fā)生器提供充足的氣流和壓力來確保液體粒子可以霧化。

1.2實驗方案

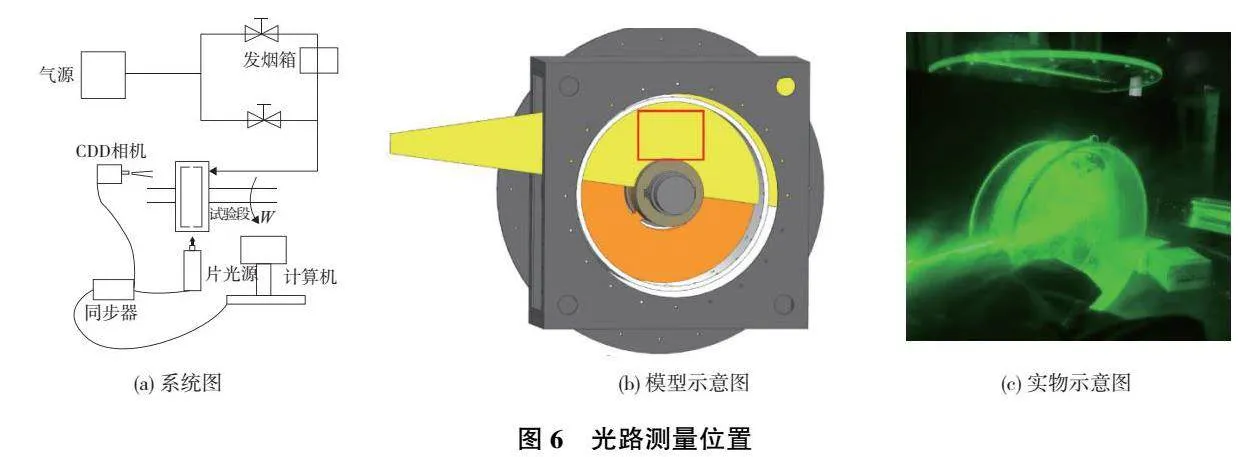
1）光路位置

光路測量位置如圖6所示。從盤腔的側(cè)面進(jìn)行激光打光，在盤腔正面拍攝，拍攝的平面為r-z平面。在圖6（b）的模型示意圖中淺灰色平面為實驗中的激光平面，其中深灰色方框為實驗的觀察窗口（本刊為黑白印刷，如有疑問請咨詢作者）。

2）實驗工況

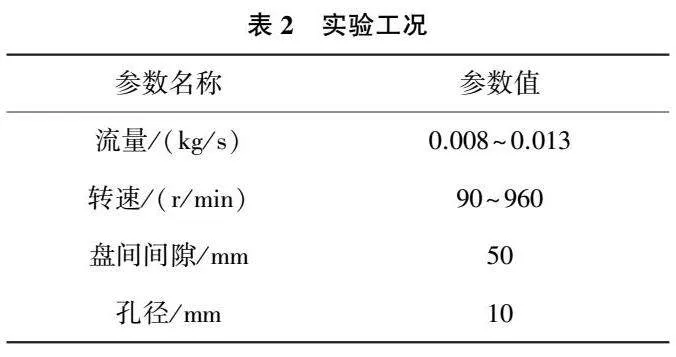
為了研究流量和轉(zhuǎn)速對于盤腔內(nèi)部旋流數(shù)和流場的影響，本文設(shè)計了24組工況，試驗工況范圍參考實際運(yùn)行工況，按照相似原理模化得到，所遵循的相似準(zhǔn)則為湍流參數(shù)。具體工況如表2所示。

實驗結(jié)構(gòu)為直型孔、盤間隙為50mm、孔徑為10mm。在氣動方面則有3個流量與8個轉(zhuǎn)速共 24種組合方式，本文一共設(shè)計了24個實驗工況。

2實驗結(jié)果及分析

2.1轉(zhuǎn)速對于內(nèi)部流場結(jié)構(gòu)的影響

1）轉(zhuǎn)速影響的速度云圖和正面實物圖

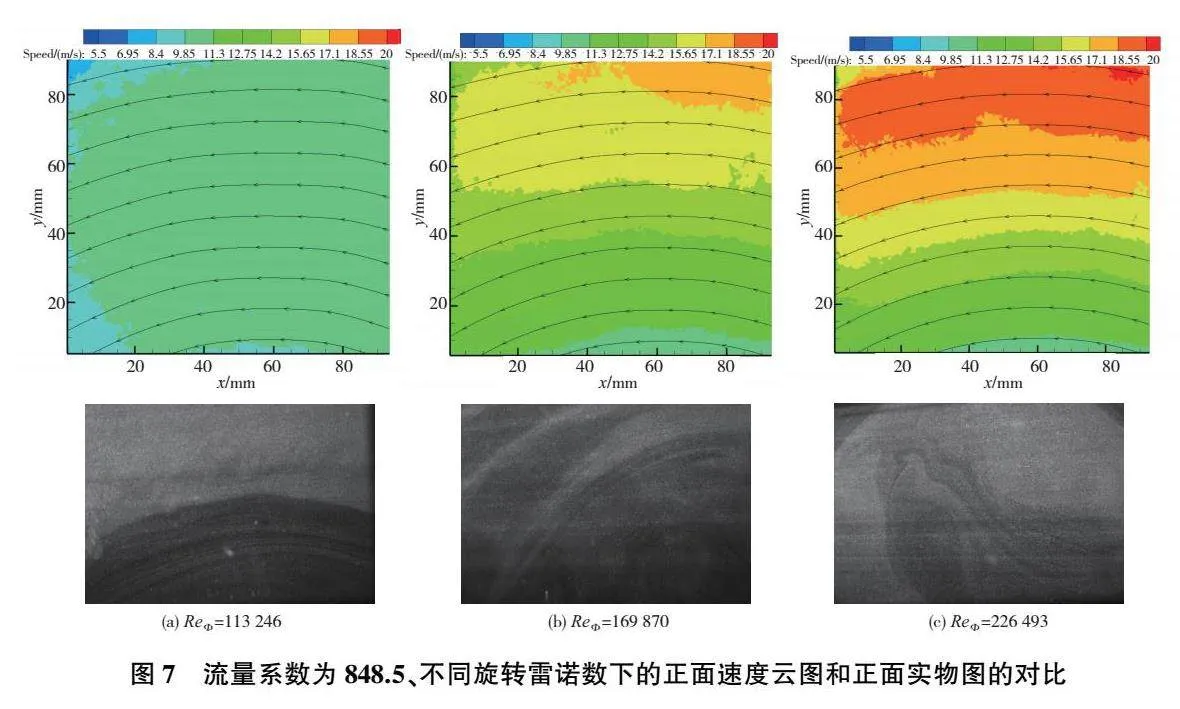
圖7所示為流量系數(shù)為848.5、不同旋轉(zhuǎn)雷諾數(shù)下的正面速度云圖對比和正面實物圖對比，旋轉(zhuǎn)雷諾數(shù)從113 246～226 493。在云圖當(dāng)中橫坐標(biāo)表示數(shù)據(jù)點位于的橫向相對位置，縱坐標(biāo)表示數(shù)據(jù)點位于的徑向相對位置。不同顏色的區(qū)域表示速度不同。在正面實物圖當(dāng)中白色的區(qū)域為流體中示蹤粒子被激光照亮的部分，可以表征流體的流動情況。

從圖7中可以看到，盤腔內(nèi)流線均是沿逆時針方向進(jìn)行轉(zhuǎn)動的。這是因為整個盤腔是以逆時針方向進(jìn)行轉(zhuǎn)動的，并且所選取的拍攝部位位于盤腔的上半部，盤腔中轉(zhuǎn)盤的內(nèi)壁面會帶動內(nèi)部流體進(jìn)行轉(zhuǎn)動。從圖中還可以看到，不同旋轉(zhuǎn)雷諾數(shù)下盤腔內(nèi)速度分布和正面的流動圖像有較大差異。在旋轉(zhuǎn)雷諾數(shù)較大的工況下，云圖中的速度分布分層明顯，有著較為清晰的顏色分界線，正面實物圖中黑色區(qū)域與白色粒子明顯摻雜。在旋轉(zhuǎn)雷諾數(shù)較小的工況下，云圖中速度的分布無明顯分層，無清晰的顏色分界線。正面實物圖中黑色區(qū)域與白色粒子區(qū)域有著清晰的分界線。這是因為在第一張圖中流場存在微弱的徑向入流，此時轉(zhuǎn)速小，旋轉(zhuǎn)效應(yīng)弱，空氣的黏性可以平衡科氏力。隨著轉(zhuǎn)速的增大，科氏力增大，此時需要很強(qiáng)的剪切力來平衡科氏力，同時增大的科氏力會抑制流體的震蕩，使得整個流場實現(xiàn)更穩(wěn)定的分層

2）轉(zhuǎn)速影響的實驗數(shù)據(jù)速度散點圖與理論非線性曲線作比較

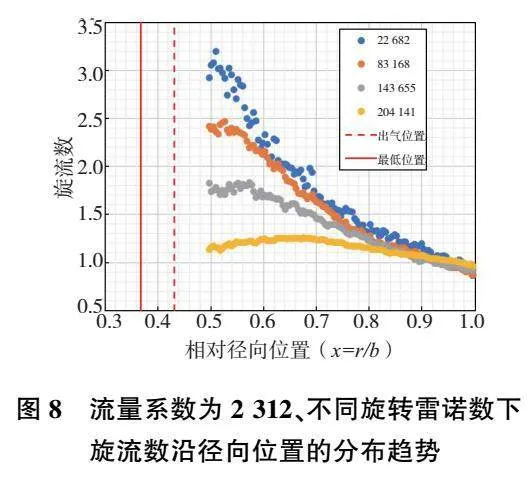
圖8所示為流量系數(shù)為2 312下的旋流數(shù)曲線對比，旋轉(zhuǎn)雷諾數(shù)從22 682～234 383。

從圖8中可以看到，盤腔內(nèi)旋流數(shù)沿徑向分布趨勢基本呈現(xiàn)出隨半徑降低而增大，并在最高徑向位置處趨于一致的特征，這是因為共性特點。這表明隨著徑向位置的下降，流體的切向速度會越來越大于轉(zhuǎn)盤的速度，使流體的切向速度超過當(dāng)?shù)剞D(zhuǎn)盤的旋轉(zhuǎn)速度，甚至數(shù)倍于當(dāng)?shù)剞D(zhuǎn)盤的旋轉(zhuǎn)速度，形成快速旋轉(zhuǎn)核心。

從圖8中還可以看到，不同旋轉(zhuǎn)雷諾數(shù)下盤腔內(nèi)的旋流數(shù)分布有較大差異。旋轉(zhuǎn)雷諾數(shù)較大的工況下，旋流數(shù)沿徑向分布呈現(xiàn)出隨半徑降低先增大后減小并且旋流數(shù)變化緩慢的特征。旋轉(zhuǎn)雷諾數(shù)較小的工況下，旋流數(shù)沿徑向分布呈現(xiàn)出隨半徑降低而增大并且旋流數(shù)快速變化。隨著轉(zhuǎn)速的增大，在盤腔中非線性曲線與實驗數(shù)據(jù)重合的區(qū)域變大，說明此時盤腔內(nèi)部強(qiáng)制渦的區(qū)域變化。而強(qiáng)制渦相比于自由渦而言，其速度變化率要小得多，這可以說明轉(zhuǎn)速越大，在相同徑向位置的旋流數(shù)越小。

OWEN適用的范圍是湍流參數(shù)λ在0.007～0.140，而在更大的氣動工況下的實驗沒有涉及，這影響了工程應(yīng)用。為了加強(qiáng)該模型的工程應(yīng)用，選擇對方程中的非線性項進(jìn)行合理調(diào)整，

這個非線性項出現(xiàn)在方程的30490πα0（β）γ0（β）項。

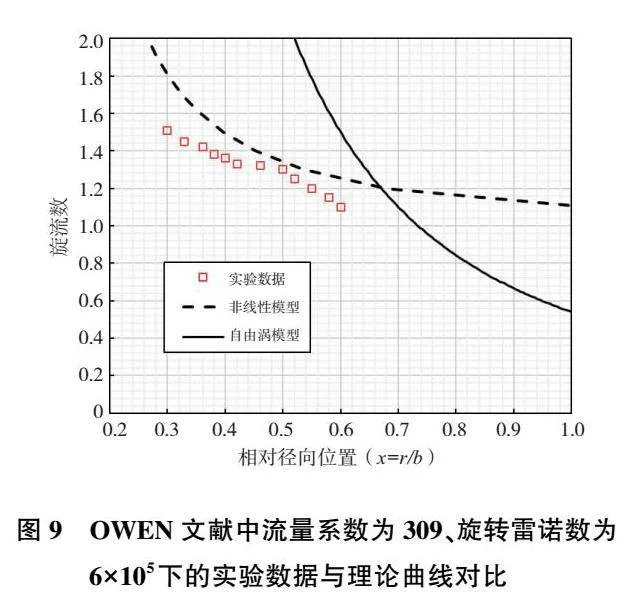
圖9OWEN文獻(xiàn)中流量系數(shù)為309、旋轉(zhuǎn)雷諾數(shù)為6×105下的實驗數(shù)據(jù)與理論曲線對比

從圖9中可以看出圖中非線性曲線會高于實驗數(shù)據(jù)的位置。這是因為OWEN文獻(xiàn)認(rèn)為圓盤附近非線性慣性和離心力與線性科氏力相比通常可以忽略不計。在這些條件下，邊界層方程（稱為旋轉(zhuǎn)參考系）簡化為黏性力和科氏力之間的平衡，得到的方程通常稱為“線性 Ekman層方程”。速度的切向分量在核心，但在 Ekman層之外，可以表示為

在線性模型的基礎(chǔ)上OWEN進(jìn)行進(jìn)一步的提升得到非線性模型，非線性模型是用來描述核心區(qū)內(nèi)部的旋流數(shù)分布的，方程如下：

對于非線性曲線每一種工況都有對應(yīng)的Ki值非線性曲線的表達(dá)式為

OWEN非線性模型只考慮了Ekman邊界層的黏性，認(rèn)為核心區(qū)的流體為無黏流體。為了進(jìn)一步加強(qiáng)工程應(yīng)用的實用性，本文把核心區(qū)流體的黏性考慮進(jìn)去，即距離邊界層不同位置的流體受到壁面的帶動作用是不同的。把30490πα0（β）γ0（β）定義為Ki，同時對于每種工況下的Ki進(jìn)行手動賦值，可以看到調(diào)整后的非線性模型與實驗數(shù)據(jù)更加吻合。

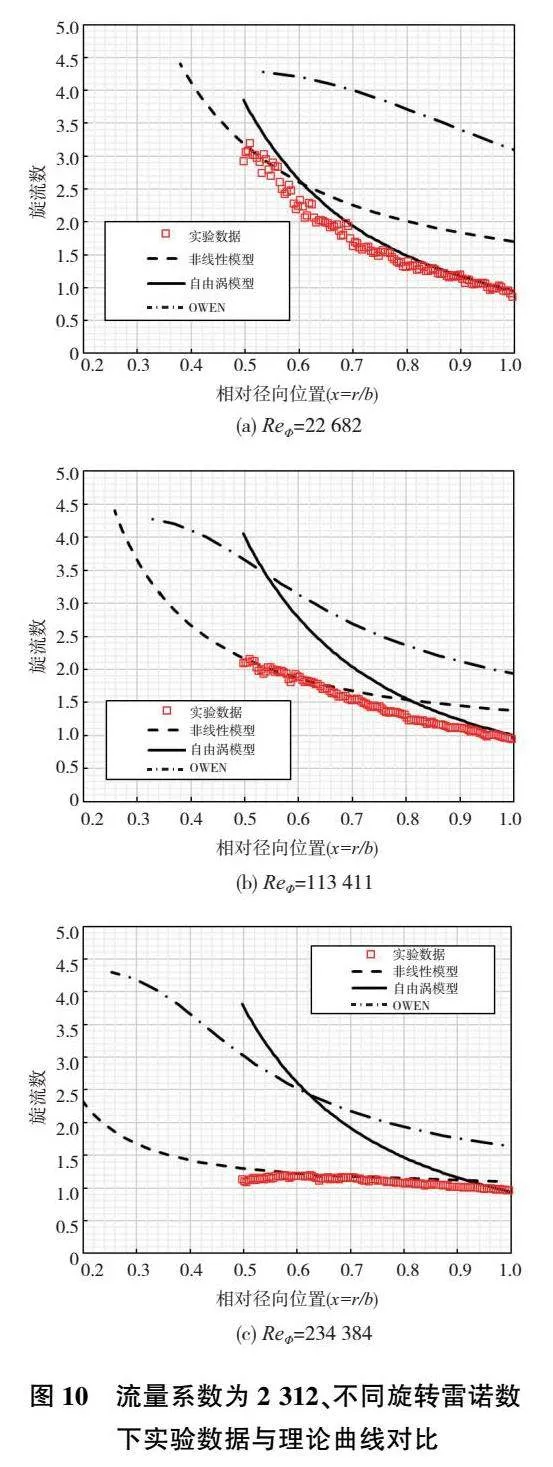
圖10為流量系數(shù)為2 312、不同旋轉(zhuǎn)雷諾數(shù)下實驗數(shù)據(jù)與理論曲線對比。

從圖10中可以看到，不同旋轉(zhuǎn)雷諾數(shù)下實驗數(shù)據(jù)與非線性曲線和自由渦曲線重合部分差異很大。在旋轉(zhuǎn)雷諾數(shù)較大的工況下，本文所得到的實驗數(shù)據(jù)與非線性模型曲線重合的部分多，與自由渦模型曲線重合部分少。在旋轉(zhuǎn)雷諾數(shù)較小的工況下，本文所得到的實驗數(shù)據(jù)與非線性模型曲線重合的部分少，與自由渦模型曲線重合部分多。可以得出結(jié)論：當(dāng)旋轉(zhuǎn)雷諾數(shù)增大時，實驗數(shù)據(jù)與非線性模型曲線重合的部分增加，與自由渦模型曲線重合部分減少。同時可以發(fā)現(xiàn)，本文的非線性模型曲線相比于OWEN文獻(xiàn)中的非線性模型和實驗數(shù)據(jù)更加吻合。

2.2流量對于內(nèi)部流場結(jié)構(gòu)的影響

1）流量對于速度云圖和正面實物圖的影響

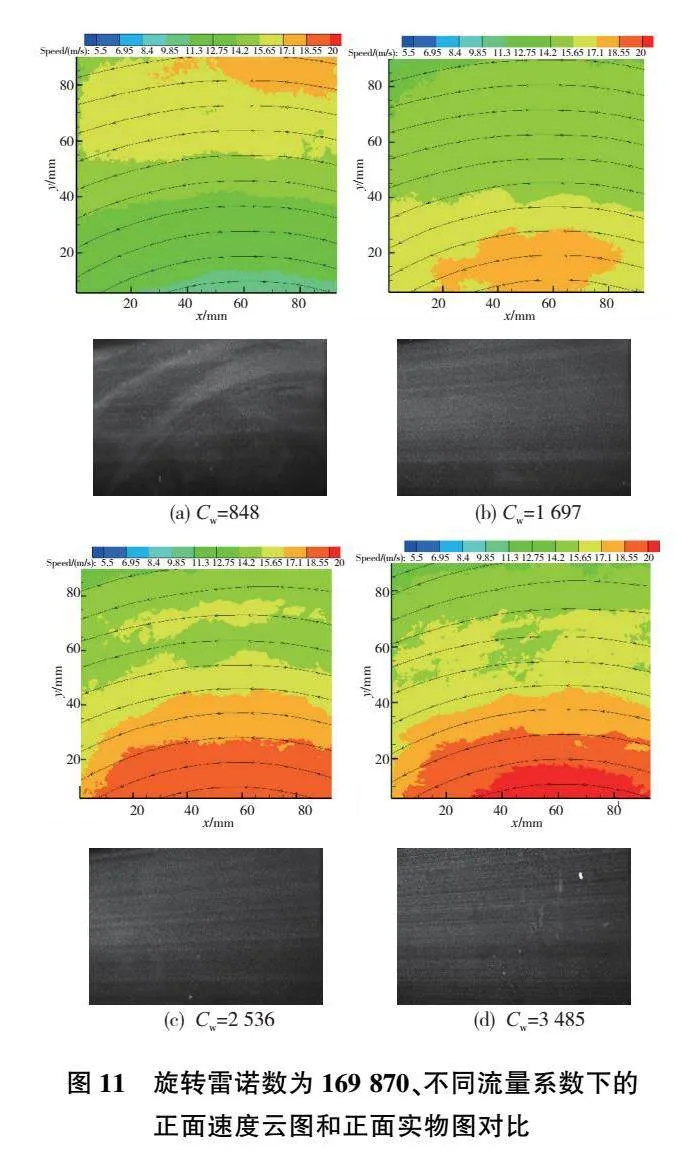
圖11為旋轉(zhuǎn)雷諾數(shù)ReΦ=169 870時的正面速度云圖和正面實物圖，流量系數(shù)從848～3 485。在云圖當(dāng)中橫坐標(biāo)表示數(shù)據(jù)點位于的橫向相對位置，縱坐標(biāo)表示數(shù)據(jù)點位于的徑向相對位置，不同顏色的區(qū)域表示速度不同。在正面實物圖當(dāng)中白色的區(qū)域為流體中示蹤粒子被激光照亮的部分可以表征流體的流動情況。

從圖11中可以看到，不同流量系數(shù)下的速度云圖和正面流動圖像有較大差異。隨著流量系數(shù)的增大，速度云圖中的速度分界線出現(xiàn)了下移的現(xiàn)象。正面實物圖中，在流量系數(shù)較小的工況下，白色的粒子與黑色區(qū)域不均勻摻雜，并以一種不規(guī)則的方式流動；在流量系數(shù)較大的工況下，白色粒子與黑色區(qū)域均勻摻雜，并以較為規(guī)則的方式流動。

2）流量影響的實驗數(shù)據(jù)速度散點圖與理論非線性曲線作比較

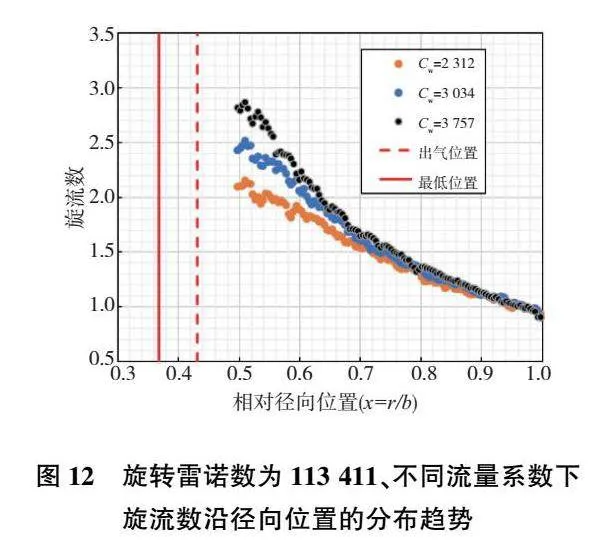
圖12所示為旋轉(zhuǎn)雷諾數(shù)為113 411時的旋流數(shù)曲線對比，流量系數(shù)從2 312～3 757。通過實驗數(shù)據(jù)與非線性曲線、自由渦曲線的對比可知，當(dāng)流量變大時，實驗數(shù)據(jù)與非線性曲線的重疊區(qū)域變小，與自由渦曲線重疊區(qū)域變大。

從圖12中看到，不同旋轉(zhuǎn)雷諾數(shù)下盤腔內(nèi)的旋流數(shù)分布有較大差異。在流量系數(shù)較大的工況下，旋流數(shù)沿徑向分布呈現(xiàn)出隨半徑降低而快速增大的特征；在旋轉(zhuǎn)雷諾數(shù)較小的工況下，旋流數(shù)沿徑向分布呈現(xiàn)出隨半徑降低而緩慢增大的特征，在相同的低徑向位置處，流量越大對應(yīng)的旋流數(shù)越大。這是因為在相同的半徑位置處Ωr是不變的，即旋流數(shù)越大的位置其流體的切向速度也越大。在轉(zhuǎn)速相同的情況下流量的上升會導(dǎo)致湍流參數(shù)值的上升，并且可以發(fā)現(xiàn)隨著流量系數(shù)的增大，實驗數(shù)據(jù)與自由渦區(qū)域的重合程度增大，自由渦入侵能力加強(qiáng)，而自由渦相比于非線性曲線而言，其旋流數(shù)的增大速率大，這可以解釋流量系數(shù)的增大會使相同徑向位置的旋流數(shù)增大。

2.3流量和轉(zhuǎn)速耦合的影響

針對流量和轉(zhuǎn)速的耦合作用，本文選取兩種無量綱參數(shù)，分別為湍流參數(shù)λ和羅斯比數(shù)Ro。

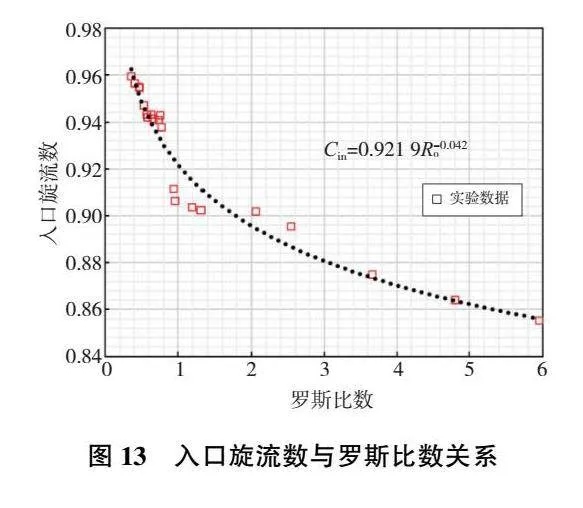
圖13所示為入口旋流數(shù)Cin隨羅斯比數(shù)變化，羅斯比數(shù)從0.354～5.950。從圖13可以得到Cin隨Ro變化的擬合公式：Cin=0.921 9R-0.042o。

從圖13中可以看到，盤腔中入口旋流數(shù)分布趨勢基本呈現(xiàn)隨著Ro增大而減小。這是因為Ro的增大會導(dǎo)致入射角的減小，而入射角的減小會使得壁面引導(dǎo)入流部分減少，慣性引導(dǎo)入流部分變大，進(jìn)而導(dǎo)致入口旋流數(shù)變大。這就可以解釋Ro的增大會導(dǎo)致入口旋流數(shù)的減小。

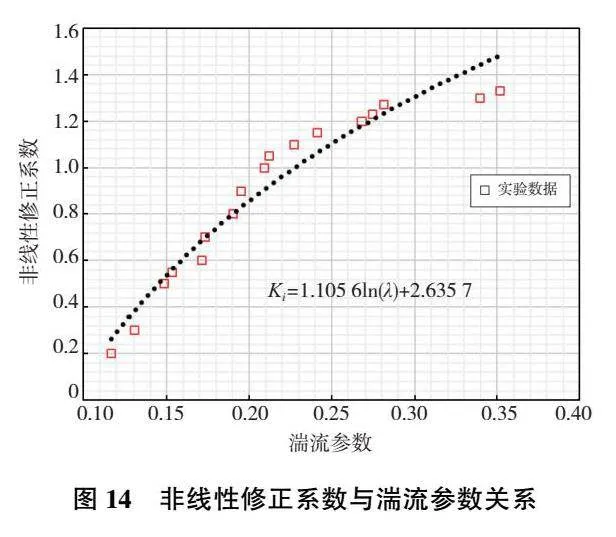
圖14所示為非線性修正系數(shù)Ki隨湍流參數(shù)λ的變化，λ從0.117～0.351。從圖14可以得到Ki隨λ變化的擬合公式：Ki=1.105 6ln（λ）+ 2.635 7。

從圖14中可以看到，盤腔中Ki分布趨勢基本呈現(xiàn)隨λ增大而增大，并且增大的速率顯現(xiàn)先快后慢的特征。

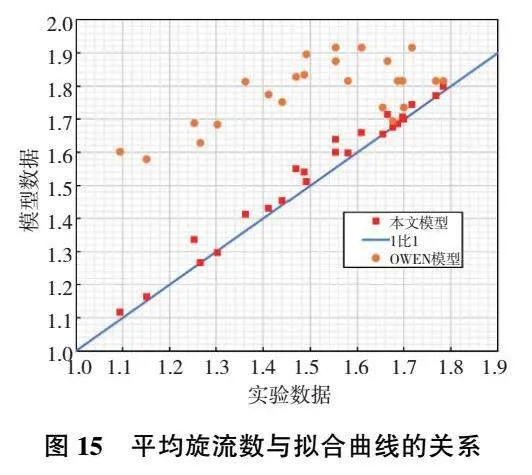
圖15為平均旋流數(shù)與擬合曲線的關(guān)系。經(jīng)計算可以得出本文的模型與實驗的誤差為1.915％，OWEN文獻(xiàn)中的理論模型與實驗的誤差為19.248％。綜上可以說明，本文的模型大大提升了模型預(yù)測的精準(zhǔn)性。

3結(jié)語

本文可以得到以下結(jié)論。

1）盤腔內(nèi)旋流數(shù)沿徑向分布趨勢基本呈現(xiàn)隨半徑降低而增大并在最高徑向位置處趨于一致的特征。

2）隨著旋轉(zhuǎn)雷諾數(shù)的增大，旋流數(shù)會減小，并且與調(diào)整后的非線性曲線重合部分增大。同時增大的科氏力會抑制流體的震蕩，使得整個流場實現(xiàn)更穩(wěn)定的分層。

3）隨著流量系數(shù)的增大，旋流數(shù)會增大，并且與自由渦曲線重合部分增大。

4）羅斯比數(shù)的增大會導(dǎo)致氣流入射角的減小，而入射角的減小會導(dǎo)致壁面引導(dǎo)入流部分的減少，慣性入流的部分變大，進(jìn)而減小入口旋流數(shù)。

5）得到了間隙比為0.263時，Ki和Cin的經(jīng)驗擬合關(guān)系式。

6）本文的模型與實驗的誤差為1.915％，OWEN文獻(xiàn)中的理論模型與實驗的誤差為19.248％，大大提升了模型預(yù)測的精準(zhǔn)性。

參考文獻(xiàn)：

［1］ 單晶葉. 核心機(jī)之路 第四代大推力軍用渦輪風(fēng)扇發(fā)動機(jī)發(fā)展（下）［J］. 航空檔案，2009（9）：56-65.

［2］ WEI S，MAO J K，YAN J X，et al. Experimental study on a hybrid vortex reducer system in reducing the pressure drop in a rotating cavity with radial inflow［J］. Experimental Thermal and Fluid Science，2020，110：109942.

［3］ WEI S，YAN J X，MAO J K，et al. A mathematical model for predicting the pressure drop in a rotating cavity with a tubed vortex reducer［J］. Engineering Applications of Computational Fluid Mechanics，2019，13（1）：664-682.

［4］ FIROUZIAN M，OWEN J M，PINCOMBE J R，et al. Flow and heat transfer in a rotating cavity with a radial inflow of fluid part 1：the flow structure［J］. International Journal of Heat and Fluid Flow，1985，6（4）：228-234.

［5］ FIROUZIAN M，OWEN J M，PINCOMBE J R，et al. Flow and heat transfer in a rotating cylindrical cavity with a radial inflow of fluid［J］. International Journal of Heat and Fluid Flow，1986，7（1）：21-27.

［6］ OWEN J M，PINCOMBE J R. Velocity measurements inside a rotating cylindrical cavity with a radial outflow of fluid［J］. Journal of Fluid Mechanics，1980，99：111-127.

［7］ 羅翔，馮軍. （2007）. 一級渦輪盤腔內(nèi)流體速度場的研究［J］. 燃?xì)鉁u輪試驗與研究（04）， 32-35.

［8］ 吉洪湖，CHEAH S C，IACOVIDES H，等. 旋轉(zhuǎn)盤腔流場速度與壓力的實驗研究［J］. 工程熱物理學(xué)報，1997，18（3）：300-305.

［9］ 趙亞濱. 用PIV測量法研究燃?xì)廨啓C(jī)葉輪與導(dǎo)葉輪間流體的速度場［J］. 熱能動力工程，1999，14（4）：28-32，85.

［10］ YAN J X，MAO J K，WEI S，et al. An investigation on the discharge coefficient of compound orifices in rotating disks［J］. Journal of Engineering for Gas Turbines and Power，2022，144（4）：041007.

收稿日期：20230324

第一作者簡介：孫肇林（1998—），男，遼寧沈陽人，碩士，研究方向為渦輪機(jī)械內(nèi)流，13624017370@qq.com。

DOI：10.19344/j.cnki.issn1671-5276.2024.06.012