基于變形補償的激光選區熔化制備空心葉片技術研究

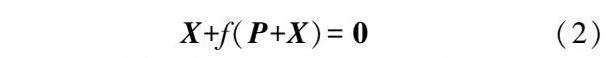
摘要：受到激光選區熔化成型機制的影響，其制件中存在較大的殘余熱應力和變形，容易導致零件制造失敗。為了解決SLM制件熱應力變形的問題，以SLM制備的316L不銹鋼空心葉片為研究對象，使用固有應變法對其進行殘余應力和變形仿真，提出一種基于體素仿真模型的變形補償方法并對其進行實驗驗證。仿真結果表明：SLM制備的316L空心葉片中殘余熱應力和熱變形較大，最大分別可達370MPa和0.2mm。實驗結果表明：該變形補償方法能明顯降低空心葉片的變形量；同原模型相比，經過變形補償后，葉片表面區域的整體偏差從0.12mm下降到了0.05mm以內。

關鍵詞：激光選區熔化；固有應變法；數值仿真；空心葉片；變形補償

中圖分類號： TH16文獻標志碼：B文章編號：1671-5276（2024）06-0078-05

Abstract：In order to solve the problems of large residual thermal stress and deformation of SLM parts affected by the SLM forming mechanism and avoid parts manufacturing failure， taking the 316L stainless Steel hollow blade prepared by SLM as the research object， proposes a deformation compensation method based on the voxel simulation model， and carries out the residual stress and deformation simulation by inherent strain method and verification by experiments. The simulation results show that the residual thermal stress and thermal deformation in the 316L hollow blade prepared by SLM are relatively large， with a maximum of 370 MPa and 0.2 mm respectively. The experimental results show that the deformation compensation method can significantly reduce the deformation of the hollow blade. And compared with the original model， the overall deviation of the blade surface， after deformation compensation， decreases from 0.12 mm to 0.05 mm within.

Keywords：selective laser melting; inherent strain method; numerical simulation; hollow blade; deformation compensation

0引言

增材制造（additive manufacturing，AM）是在 20世紀末期興起的一種依據逐層累積制造原理直接制造出實物的制造技術［1］。受益于逐層制造的方式，AM可以成型為復雜幾何形狀的結構，如拓撲結構［2］、仿生結構［3］以及晶格結構［4］等，極大地解放了設計自由度。激光選區熔化（selective laser melting， SLM）是目前發展最成熟、應用最廣泛的金屬增材制造技術。然而SLM成形因受其快速熔凝機制的影響，制件中存在較大的殘余應力，易使模型發生變形甚至開裂，使制造失敗。國內外許多學者對如何消除變形開展了一系列的研究。AFAZOV等［5］模擬了SLM制備的17-4合金鋼葉片的變形，并對原CAD模型進行逆向補償以減小制件的變形。研究結果表明：通過逆向補償后模型的制造結果更貼近于原始設計尺寸，其變形量在±45μm以內，遠小于原始模型直接打印的結果（±200μm）。劉檢華等［6］以螺旋槳結構成型為例，提出了利用變形場反饋調整零件設計的幾何結構的方法。研究結果表明：經過4次變形場補償迭代計算，螺旋槳構件最大變形量由最初的1.690mm下降到0.087mm，降幅達94%。以上研究中的變形補償技術雖然能夠有效降低零件的變形量，但是仿真計算配合逆向補償操作需要多次迭代計算，耗費大量的計算資源和時間，另一方面通過實驗測量和逆向補償的方式需要耗費較大的實驗成本，故這些方法很難直接應用于生產實踐中。本文使用Simufact additive軟件，基于固有應變法直接對SLM制備的316L空心葉片進行應力場和變形仿真，提出一種基于體素仿真模型的變形逆補償方法，以快速求解逆補償模型。

1基于固有應變法的空心葉片仿真

1.1材料參數及有限元模型

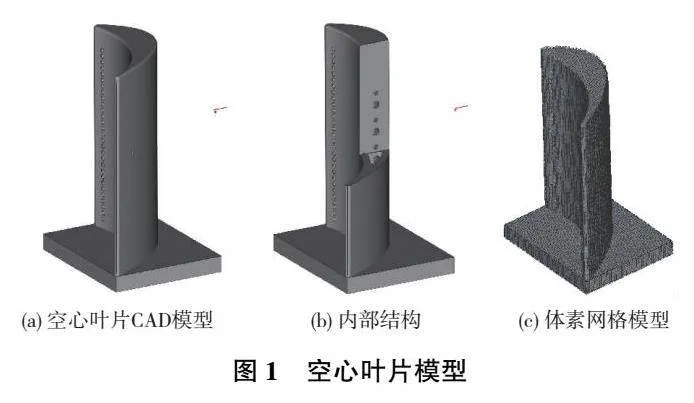
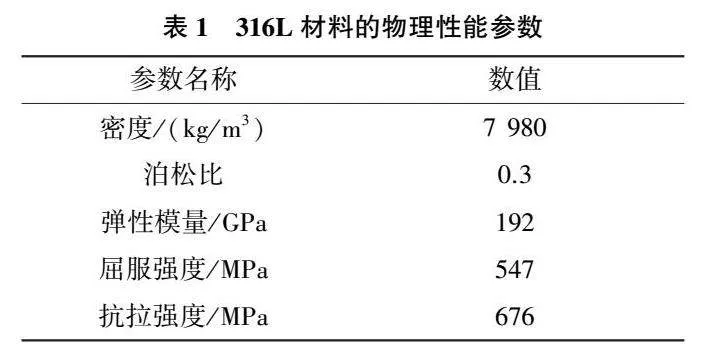
在空心葉片的固有應變法仿真過程中，316L不銹鋼材料的密度、泊松比、彈性模量、屈服強度及抗拉強度等性能參數值取為常數，如表1所示。該葉片的整體高度為48.5mm，內部為空心結構，厚度為1.5mm。在有限元模型中，網格類型選擇了六面體單元（體素網格）。通過分析網格尺寸的影響，選擇0.4mm的網格尺寸較為合適，葉片體素網格數量為138100個，節點數為168157個，層數為122層，具體的空心葉片模型如圖1所示。仿真與實驗使用的工藝參數組合為激光功率200W、掃描速度0.9m/s、層厚60μm、光斑直徑0.09mm、掃描間隔0.1mm、掃描路徑S形，其余參數值按設備默認值。同時在該打印工作中，使用的是氣霧化的316L粉末，直徑為15μm ～53μm，其質量分數如表2所示。

1.2基于固有應變法的空心葉片的變形及殘余應力分布

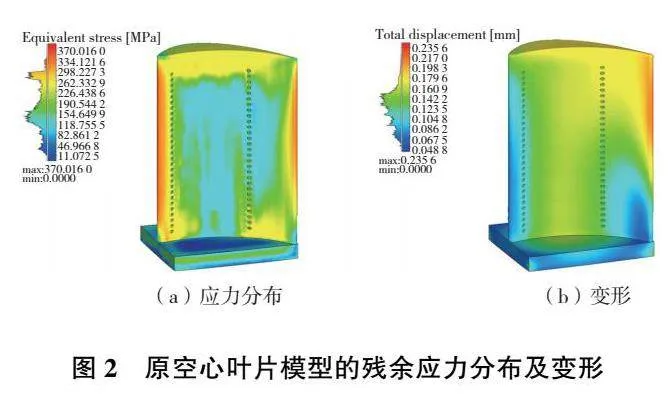
圖2為空心葉片原始模型在基于固有應變法的Simufact additive軟件仿真計算出來的Von-Mises應力分布圖和整體變形圖。從圖2（a）可以發現，原模型上的Von-Mises應力最大可達370MPa，主要集中在葉片的左右兩側和頂部，大部分位置應力在300MPa以內；從圖2（b）可以發現，葉片的最大變形量為0.235 6mm，發生在葉片的右側邊緣處，整體變形主要集中在0.08mm～0.15mm區域內。

2SLM成形的變形逆補償技術

2.1變形逆補償原理

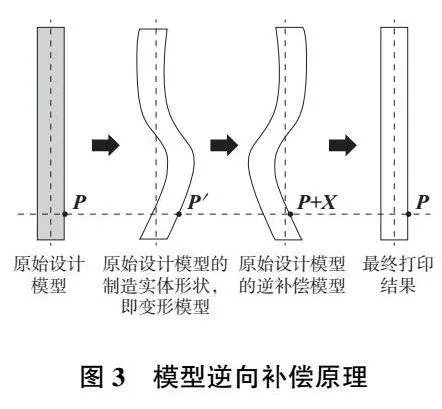
在整個制造業中，生產的零件需要滿足設計公差要求。然而在金屬3D打印中，由于殘余熱應力的存在，零件會發生變形。如圖3所示，AFAZOV等［7］提出了模型逆向補償的概念，即通過對模型做反向補償，利用殘余熱應力變形，使打印的零件變形到原始的設計尺寸。

逆補償原理為：對于原模型上給定的點P=xPypzPT，即找到逆變形矢量X=xyzT滿足式（1）：

式中：P為原模型上給定的點（xP，yp，zP）；X為逆向補償矢量（x，y，z）；f（P+X）∈R3×1為補償后的點P+X處產生的變形量，為X的函數。消除等式兩邊的P后，該問題可以轉換為尋找式（2）的解。

然而要求解該方程，必須要解決兩個主要問題［8］：

1）對于原始模型和制造后的變形模型，如何捕捉模型上每個點的物理變形，從而計算出對于給定點P的變形量f；

2）f（P+X）是關于X的函數，但是該函數未知且非線性，如何找到滿足或者更好的近似式（2）中的X值。

為此，本文提出一種基于固有應變仿真模型的變形逆補償方法，用于減少SLM成形制件的變形量。

2.2基于固有應變法仿真模型的變形逆補償方法

基于固有應變仿真模型的變形逆補償方法，即使用仿真的變形結果作為零件的實際變形量，然后求解逆補償量，并生成逆補償模型。具體步驟如下。

1）固有應變法仿真。首先使用固有應變法對空心葉片模型進行應力場和變形量進行仿真計算，并得出空心葉片體素模型的應力分布和變形量。

2）根據節點坐標計算原始設計模型的變形量。由于原始設計模型采用的是STL格式，而固有應變法仿真采用的是體素單元模型，需要將體素單元的節點變形量映射到STL的三角面片頂點上。具體插值方法如2.3節所述。

3）判斷變形量是否滿足模型設計的需求。比較步驟2）中所得的變形量與設計的最大允許偏差，如果滿足設計需求，則可以直接制造上述模型；反之，則需要對模型進行逆變形補償，執行步驟4）。

4）根據三角面片的頂點坐標以及變形量生成仿真預測的變形模型（本文將該模型等同于實體制造形狀，即忽略仿真與制造誤差）。本文采用頂點坐標直接偏移的方式來生成該變形模型，即將頂點坐標與變形矢量直接相加作為新的頂點坐標，不改變三角面片本身的拓撲關系。

5）計算逆變形補償量。根據預測的變形模型與形狀目標（原始設計模型）之間的差值近似計算式（2）的根X，其具體的計算方式如2.4節所述。

6）生成逆變形補償模型，并重復步驟1）—步驟3）直至誤差結果符合設計需求。

2.3原STL模型的變形量計算方法

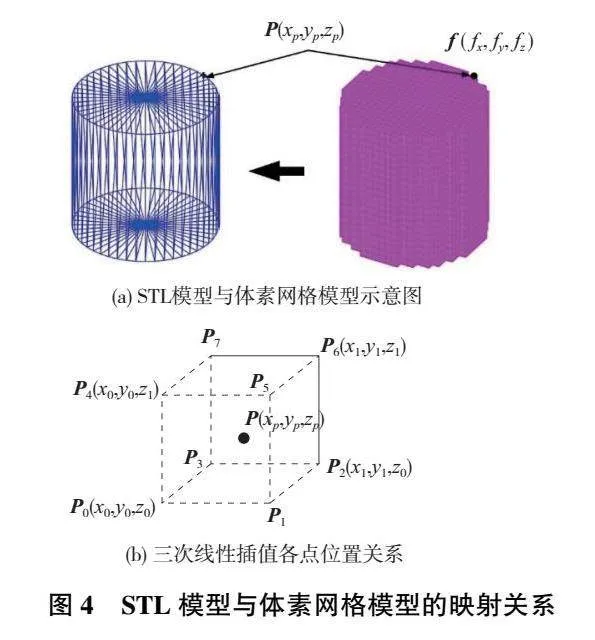
通過固有應變法的仿真可以得到原模型的變形量，然而固有應變法使用的是有限元體素模型，而非原始設計的STL模型，因此需要將體素模型各節點的變形量映射到原始設計的STL模型上，如圖4（a）所示。

本文采用三次線性插值（trilinear interpolation）的方式來計算原始設計的空心葉片STL模型的變形量。對于給定的點P，其變形量f（P）包含x， y， z 3個方向分量，并且每個分量均為點坐標（xp，yp，zp）的函數，即

對于體素單元來講，其8個頂點的變形矢量已知，因此只需要搜索包含P點的體素單元（若無包含，則選擇距離最近的體素單元），然后采用三次線性插值的方式求解fk（xp，yp，zp），其計算方式如式（4）所示。

式中：k=x，y，z；Δx、Δy、Δz是點P分別在x、y、z方向與體素單元起點P0的相對距離，其位置關系如圖4（b）所示，即

記Ck=［c0c1c2c3c4c5c6c7］T ，則有 Ck=BDk。其中：

2.4逆向變形補償計算方法

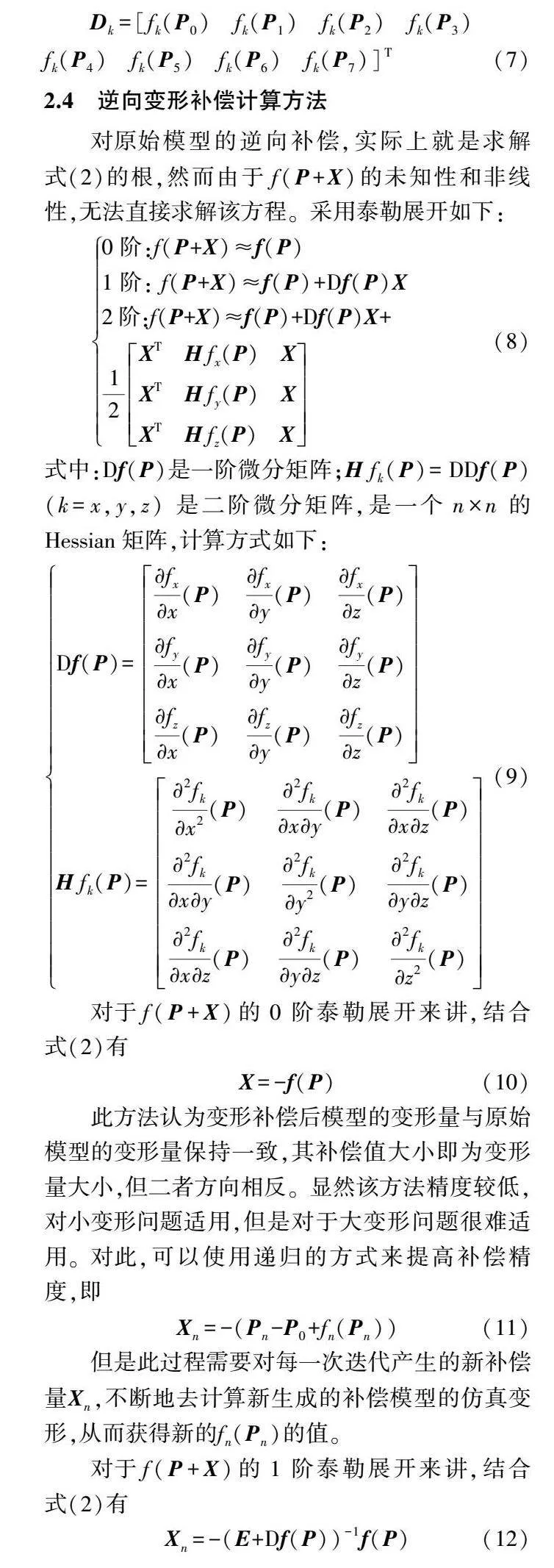
對原始模型的逆向補償，實際上就是求解式（2）的根，然而由于f（P+X）的未知性和非線性，無法直接求解該方程。采用泰勒展開如下：

0階：f（P+X）≈f（P）

1階： f（P+X）≈f（P）+Df（P）X

2階：f（P+X）≈f（P）+Df（P）X+12XTHfx（P）X

式中：Df（P）是一階微分矩陣；Hfk（P）=DDf（P）（k=x，y，z） 是二階微分矩陣，是一個n×n 的Hessian矩陣，計算方式如下：

對于f（P+X）的0階泰勒展開來講，結合式（2）有

此方法認為變形補償后模型的變形量與原始模型的變形量保持一致，其補償值大小即為變形量大小，但二者方向相反。顯然該方法精度較低，對小變形問題適用，但是對于大變形問題很難適用。對此，可以使用遞歸的方式來提高補償精度，即

但是此過程需要對每一次迭代產生的新補償量Xn，不斷地去計算新生成的補償模型的仿真變形，從而獲得新的fn（Pn）的值。

對于f（P+X）的1階泰勒展開來講，結合式（2）有

式中E為3×3的單位矩陣。此方法即認為在執行一次變形補償操作中，新模型的變形量和補償量是一個線性函數。同0階的泰勒展開一樣，也可以使用遞歸的方式來提高補償精度，即

另外， 對于二階及以上的展開，首先其方程求解過于復雜，其次本身變形量就是一個微小的數值，其二階偏導的影響微乎其微，因此本文不做討論。

3空心葉片變形補償結果分析與實驗驗證

3.1空心葉片的補償結果

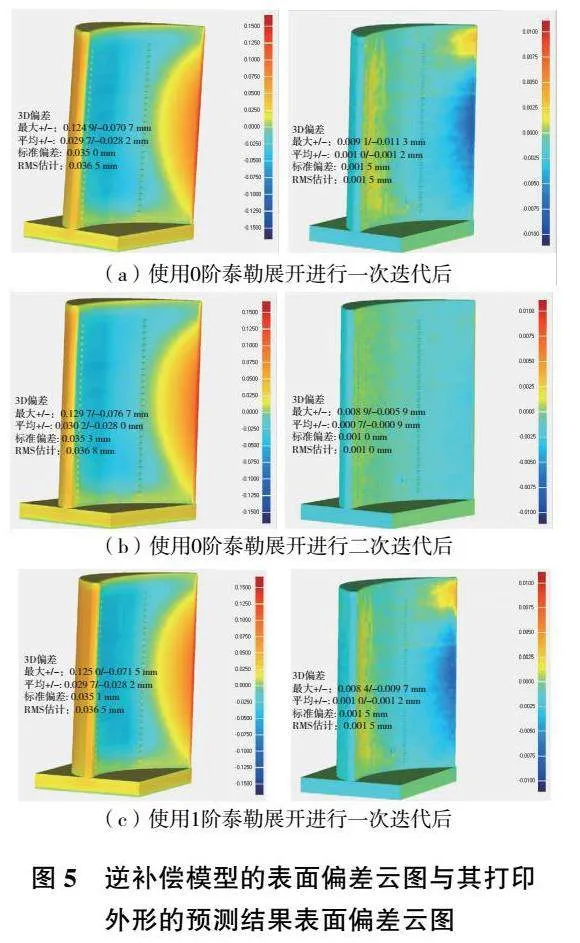
圖5為逆補償模型的表面偏差云圖與其打印外形的預測結果表面偏差云圖。如圖5（b） 所示，二次迭代的逆補償結果將最終零件的表面偏差從原始的0.235 6mm降低到了0.015 0mm以內，這表明變形逆補償操作確實可以極大地提高SLM制備空心葉片的外形精度。同時，從圖5中可以發現，0階泰勒展開一次迭代、0階泰勒展開二次迭代以及1階泰勒展開一次迭代的逆補償結果之間只存在微米級別的差距。從其打印外形的預測結果表面偏差云圖可以發現，0階泰勒展開二次迭代要明顯優于0階泰勒展開一次以及1階泰勒展開一次補償迭代的結果。

盡管對比最大偏差，1階泰勒展開逆補償的結果要優于0階泰勒展開，但是其偏差僅僅從原來的（0.009 1/-0.011 3）mm降低到了（0.008 9/-0.009 7）mm，變化量微乎其微。其原因可能是：該葉片本身的變形量只有0.235 6mm，這一值非常小，導致其空間域上的1階偏導數矢量非常小，從而使得變形的空間變化量在計算中幾乎不起作用，最終造成0階展開與1階展開的計算結果差異性不大。

3.2實驗驗證

選取原葉片模型以及0階泰勒展開第二次迭代的逆補償模型作為對比，進行實驗驗證。打印完成后使用測量精度為0.01mm的藍光三維掃描儀掃描葉片的表面，獲得其三維數字模型，然后使用Geomagic Control軟件對其同原始設計模型進行最佳擬合匹配，計算表面偏差。打印樣件如圖6（a）所示（其中左側為原幾何體生成的葉片，右側為變形逆補償后幾何體生成的葉片），二者成型結果較好，表面光滑有金屬色澤，無肉眼可見的缺陷、裂紋等。尺寸方面，二者亦無明顯差異。打印結果和設計模型的偏差如圖6（b）所示（其中左側為原幾何體生成的葉片，右側為變形逆補償后幾何體生成的葉片）。從圖6（b）中可以發現，經過逆補償后的模型打印結果整體偏差遠小于原始設計模型的打印結果整體偏差。在逆補償后，葉片表面區域的整體偏差從0.12mm下降到了0.05mm以內。原設計模型的打印結果偏差主要集中在葉片的左右兩側以及頂部區域，這與仿真殘余應力分布結果以及變形結果一致，這也說明了固有應變法仿真結果的可靠。

4結語

為了解決SLM制件熱應力變形的問題，保證一次制造成功，本文以SLM制備的316L空心葉片為研究對象，開發了一種基于體素仿真結果的變形逆補償方法，并對其進行實驗驗證。結論如下。

1）SLM制備的316L空心葉片中存在較大的殘余應力以及變形，其Von-Mises應力最大可達370MPa，變形量最大可達0.2mm。

2）仿真計算結果表明，盡管采用1階泰勒展開時模型的逆補償結果要優于0階的結果，但是其差異性非常小。同時，實驗結果表明該變形逆補償方法可以有效地降低原設計模型的打印偏差。經過補償后，葉片的表面偏差從0.12mm下降到0.05mm以內。

參考文獻：

［1］ 盧秉恒，李滌塵. 增材制造（3D打印）技術發展［J］. 機械制造與自動化，2013，42（4）：1-4.

［2］ 劉書田，李取浩，陳文炯，等. 拓撲優化與增材制造結合：一種設計與制造一體化方法［J］. 航空制造技術，2017，60（10）：26-31.

［3］ ZHANG Y C，WANG Z P，ZHANG Y C，et al. Bio-inspired generative design for support structure generation and optimization in Additive Manufacturing （AM）［J］. CIRP Annals，2020，69（1）：117-120.

［4］ LEBAAL N，ZHANG Y C，DEMOLY F，et al. Optimised lattice structure configuration for additive manufacturing［J］. CIRP Annals，2019，68（1）：117-120.

［5］ AFAZOV S，DENMARK W A D，LAZARO TORALLES B，et al. Distortion prediction and compensation in selective laser melting［J］. Additive Manufacturing，2017，17：15-22.

［6］ 劉檢華，任策，夏煥雄，等. 基于仿真的選區激光熔化工藝結構變形補償設計優化［J］. 北京理工大學學報，2021，41（9）：911-917.

［7］ AFAZOV S，SEMERDZHIEVA E，SCRIMIERI D，et al. An improved distortion compensation approach for additive manufacturing using optically scanned data［J］. Virtual and Physical Prototyping，2021，16（1）：1-13.

［8］ XU K，KWOK T H，ZHAO Z C，et al. A reverse compensation framework for shape deformation control in additive manufacturing［J］. Journal of Computing and Information Science in Engineering，2017，17（2）：021012.

收稿日期：20230424

第一作者簡介：于晨瀟（1994—），男，浙江義烏人，碩士研究生，研究方向為增材制造，yu_chenxiao@foxmail.com。

DOI：10.19344/j.cnki.issn1671-5276.2024.06.015