“四活”交響曲，奏響教學(xué)新樂(lè)章

［摘 要］數(shù)學(xué)新課標(biāo)在“三角形的三邊關(guān)系”教學(xué)中新增了尺規(guī)作圖這一內(nèi)容，旨在讓學(xué)生感受尺規(guī)作圖價(jià)值的同時(shí)，發(fā)展他們的推理意識(shí)、幾何直觀、空間觀念等素養(yǎng)。課堂上，教師可通過(guò)提出猜想、演繹推理、拓展應(yīng)用等活動(dòng)，引導(dǎo)學(xué)生直觀感悟三角形的三邊關(guān)系，體驗(yàn)規(guī)律探索的樂(lè)趣和挑戰(zhàn)，使學(xué)生能根據(jù)三角形的三邊關(guān)系解決生活中簡(jiǎn)單的實(shí)際問(wèn)題，促進(jìn)學(xué)生數(shù)學(xué)核心素養(yǎng)的提升。

［關(guān)鍵詞］三角形；三邊關(guān)系；推理意識(shí)；尺規(guī)作圖

［中圖分類(lèi)號(hào)］ G623.5 ［文獻(xiàn)標(biāo)識(shí)碼］ A ［文章編號(hào)］ 1007-9068（2024）36-0018-04

【教學(xué)內(nèi)容】

蘇教版數(shù)學(xué)教材四年級(jí)下冊(cè)第77～78頁(yè)的例3，“練一練”中的第1～2題，練習(xí)十二中的第6～8題。

【教學(xué)目標(biāo)】

1.通過(guò)尺規(guī)作圖等活動(dòng)，直觀感悟三角形的三邊關(guān)系，理解“任意兩邊長(zhǎng)度的和大于第三邊”這一規(guī)律。

2.通過(guò)猜測(cè)、推理、驗(yàn)證、數(shù)據(jù)分析等方法感悟三角形三邊關(guān)系的規(guī)律，會(huì)判斷給定的線段長(zhǎng)度能否組成三角形，并能解釋生活實(shí)際中的現(xiàn)象，解決生活中簡(jiǎn)單的實(shí)際問(wèn)題。

3.積累活動(dòng)經(jīng)驗(yàn)，體驗(yàn)規(guī)律探索的樂(lè)趣和挑戰(zhàn)，發(fā)展空間觀念和推理意識(shí)等素養(yǎng)。

【教學(xué)重點(diǎn)】

借助尺規(guī)作圖，探究與推理三角形的兩邊之和大于第三邊的關(guān)系。

【教學(xué)難點(diǎn)】

理解“任意”的含義，歸納三角形的三邊關(guān)系，發(fā)展學(xué)生的推理意識(shí)。

【教學(xué)過(guò)程】

一、課前談話，激發(fā)興趣（略）

【評(píng)析】教師教學(xué)前播放視頻，讓學(xué)生感受三角形的變化與神秘，有助于激發(fā)學(xué)生探索的欲望。

二、引出問(wèn)題，提出猜想

1.三點(diǎn)共線不能?chē)扇切?/p>

師：什么樣的圖形是三角形？它有什么特征？

生1：3條線段首尾相接圍成的圖形是三角形，它有3個(gè)頂點(diǎn)、3條邊、3個(gè)角。

師：有3個(gè)點(diǎn)是不是一定能?chē)扇切危?/p>

生2：兩點(diǎn)確定一條線段，只要第三個(gè)點(diǎn)不在同一直線上，就可以圍成一個(gè)三角形。

2.提出猜想

師：有3條線段是不是一定能?chē)扇切危?/p>

生3：一定能。

生4：不一定。

【評(píng)析】教師從三角形的特征出發(fā)，提出“有3條線段是不是一定能?chē)扇切巍边@一問(wèn)題，促進(jìn)使學(xué)生深入思考。這樣教學(xué)，從三角形點(diǎn)的位置關(guān)系遷移到邊的關(guān)系，給學(xué)生探究角的關(guān)系留下了想象的空間。

三、操作推理，感悟規(guī)律

1.操作探究，分類(lèi)歸納

師：（出示圖1）a、b、c、d這4條線段，任意3條都能?chē)扇切螁幔?/p>

生5：需要驗(yàn)證。

師：能不能用尺規(guī)來(lái)研究它們之間的關(guān)系？誰(shuí)來(lái)展示不能?chē)扇切蔚那闆r？

生6：a、b、c和a、c、d這兩組線段圍不成三角形。

師：在a、b、c這3條線段圍不成三角形的情況中，有交點(diǎn)為什么不能?chē)扇切危窟@3條線段有什么關(guān)系？

生7：這交點(diǎn)是第三個(gè)交點(diǎn)，由于三點(diǎn)共線，即a+b=c，所以圍不成三角形。

生8：a、c、d這3條線段也圍不成三角形。

師：為什么不能?chē)扇切危繛槭裁催@里沒(méi)有交點(diǎn)？

生9：由于a+d<c，所以不可能有交點(diǎn)。

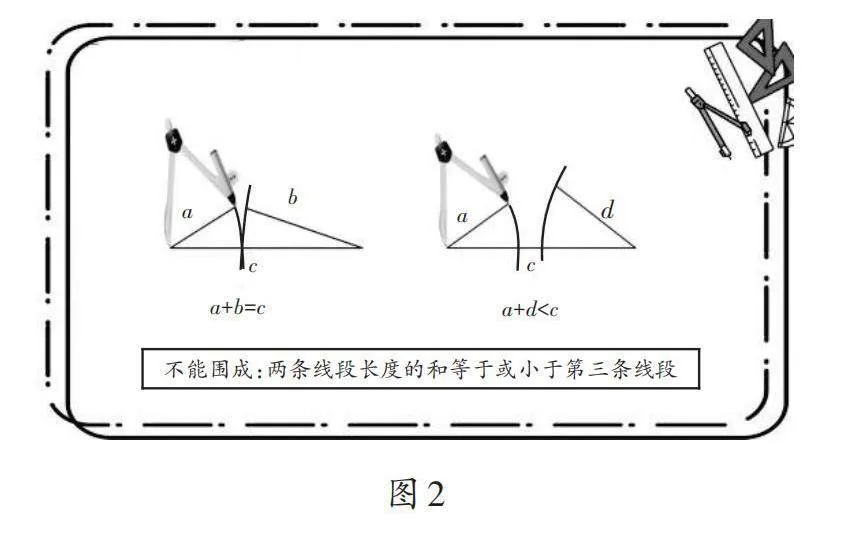
師：通過(guò)探究發(fā)現(xiàn)，a、b、c和a、c、d這兩組線段都不能首尾相接圍成三角形。想一想，不能?chē)扇切蔚?條線段有怎樣的關(guān)系？

生10：（出示圖2）不能?chē)扇切蔚?條線段，其中2條線段長(zhǎng)度的和小于或等于第3條線段。

師：有能?chē)扇切蔚那闆r嗎？

生11：a、b、d和b、c、d這兩組線段能?chē)扇切巍?/p>

師：為什么能?chē)扇切危?/p>

生12：有交點(diǎn)，且交點(diǎn)在線段外。

師：那么，能?chē)扇切蔚?條線段有什么關(guān)系？

生13：a+d>b、b+d>c，即其中兩條線段長(zhǎng)度的和大于第三條線段。

【評(píng)析】為提高學(xué)生的參與度，教師預(yù)留了自主探索的空間，鼓勵(lì)學(xué)生展示自己的學(xué)習(xí)單，圍繞三角形的三邊關(guān)系提出問(wèn)題。這樣教學(xué)，有利于引發(fā)學(xué)生的深度思考，幫助學(xué)生自主建構(gòu)三角形的認(rèn)知。

2.深入探究，揭示關(guān)系

師：到底什么樣的3條線段才能?chē)扇切危?/p>

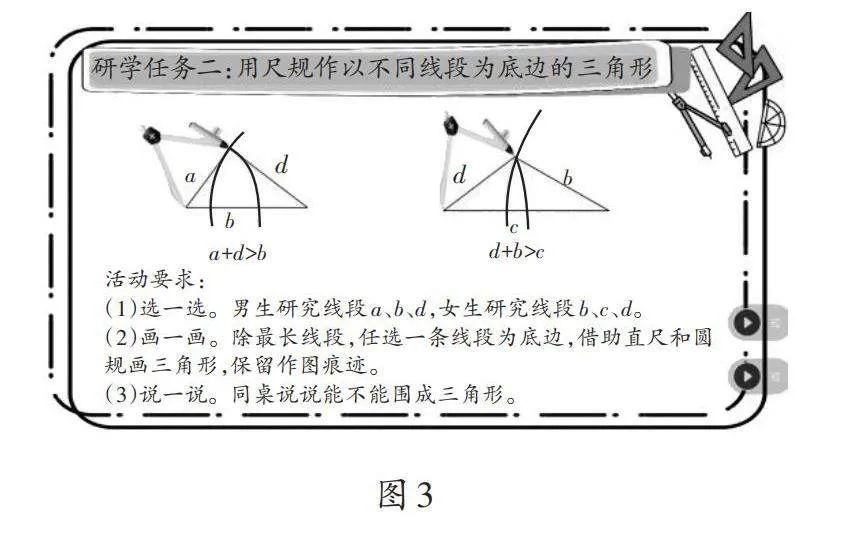
生14：以另外2條線段為底再來(lái)畫(huà)一畫(huà)，看看有什么關(guān)系。（教師出示圖3）

（1）引出“任意”

師：請(qǐng)男生來(lái)展示，你們以哪條線段為底？能?chē)扇切螁幔窟@3條線段有什么關(guān)系？

生15：我們以線段d或a為底，能?chē)扇切危驗(yàn)閍+b>d或b+d>a。

生16：我們發(fā)現(xiàn)任意兩條線段長(zhǎng)度的和大于第三條線段能?chē)扇切巍?/p>

師：男生用“任意”二字來(lái)描述這3條線段的關(guān)系。那另一個(gè)三角形也是這樣嗎？請(qǐng)女生來(lái)展示。（女生交流與男生交流一致，得到一樣的結(jié)論）

（2）理解“任意”

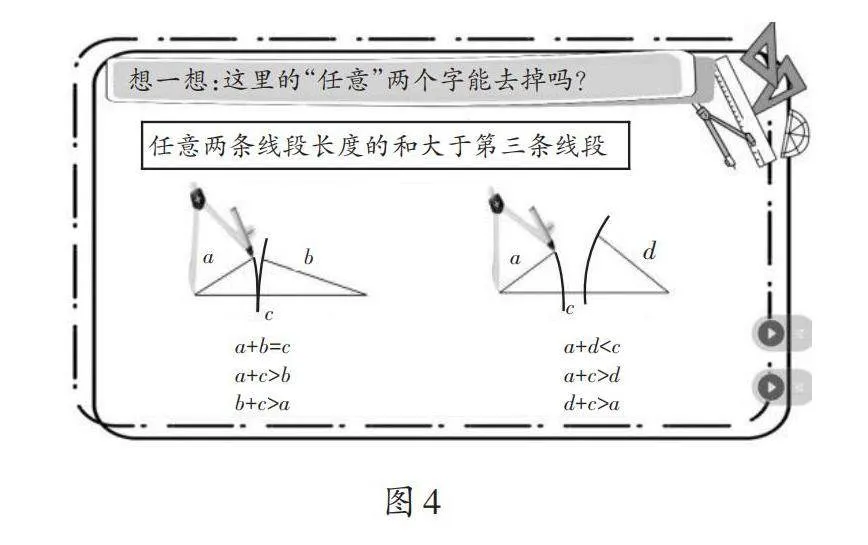
師：（出示圖4）想一想，把“任意”兩個(gè)字去掉，可以嗎？觀察不能?chē)扇切蔚那闆r，你們能完整地說(shuō)一說(shuō)這3條線段之間的關(guān)系嗎？（學(xué)生完整地說(shuō)出了這3條線段之間的關(guān)系）

師：我發(fā)現(xiàn)這里也有兩條線段長(zhǎng)度的和大于第三條線段，可它們?yōu)槭裁床荒車(chē)扇切文兀?/p>

生17：有兩條線段長(zhǎng)度的和不是大于第三條線段。

師：看來(lái)，“任意”兩個(gè)字不能去掉。

【評(píng)析】 通過(guò)“猜想—驗(yàn)證—舉反例—得出結(jié)論”，教師著重解釋“任意”一詞的意思，使學(xué)生明確“任意”一詞不能刪去，真正理解了所學(xué)知識(shí)。

3.數(shù)據(jù)論證，得出結(jié)論

師：是不是所有的三角形都有這樣的三邊關(guān)系呢？

生18：可以任意畫(huà)一個(gè)三角形來(lái)探究、驗(yàn)證。

師：（借助幾何畫(huà)板隨意拖動(dòng)三角形的一個(gè)頂點(diǎn)）三角形的形狀和大小怎么樣了？它的三邊關(guān)系呢？（師生交流發(fā)現(xiàn)）

師生（小結(jié)）：我們從不能?chē)珊湍車(chē)扇切蔚膬煞N情況，對(duì)其進(jìn)行了研究和驗(yàn)證，最終得出了“三角形任意兩邊長(zhǎng)度的和大于第三邊”的結(jié)論。

【評(píng)析】上述教學(xué)，從個(gè)別到一般、從特殊到普遍，使學(xué)生深刻理解了“三角形任意兩邊長(zhǎng)度的和大于第三邊”這一知識(shí)點(diǎn)。

4.方法優(yōu)化，形成能力

師：（出示2、5、6，2、4、6，2、2、5這三組線段長(zhǎng)度）這三組線段能否圍成三角形？（學(xué)生回答后）還有沒(méi)有更好的判斷方法？

生19：能?chē)扇切蔚娜龡l線段中，兩條較短線段長(zhǎng)度的和大于最長(zhǎng)的線段，那么最長(zhǎng)的線段加上其中一條較短線段，一定大于另一條較短的線段。

師：如果是a、b、c這3條線段呢？你也能說(shuō)說(shuō)怎么判斷它們能否圍成三角形嗎？

生20：a+b>c。

師：為什么？（學(xué)生推理說(shuō)明）如果a、b、c這3條線段，有2條線段一樣長(zhǎng)呢？這3條線段一樣長(zhǎng)呢？（學(xué)生推理說(shuō)明）

師：不管是怎樣的3條線段，判斷的道理是一樣的。只要發(fā)現(xiàn)兩條較短線段長(zhǎng)度的和大于第三條線段，就能判斷這3條線段能否圍成三角形。

【評(píng)析】上述教學(xué)，教師通過(guò)問(wèn)題促使學(xué)生不斷發(fā)散思維，有效培養(yǎng)了學(xué)生的歸納總結(jié)能力和思維能力。同時(shí)，教師用字母表示線段的長(zhǎng)度，從特殊到一般，使問(wèn)題更具一般性和抽象性，深化了學(xué)生對(duì)三角形三邊關(guān)系的理解。

四、演繹推理，論證歸納

1.情境導(dǎo)入，事實(shí)論證

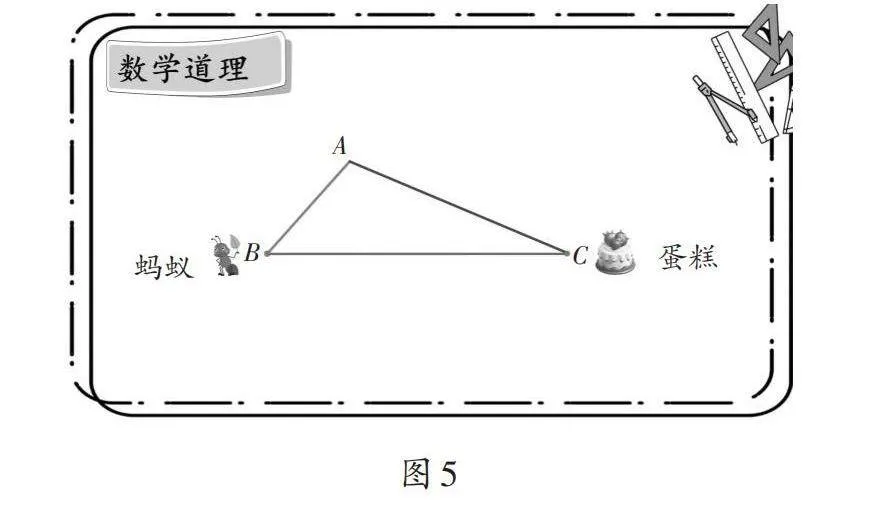
師：（出示圖5）看，這有一只螞蟻。它想要吃這塊蛋糕，該選哪條路呢？你們想到了以前學(xué)過(guò)的什么知識(shí)？

生21：兩點(diǎn)之間線段最短。

2.回顧舊知，驗(yàn)證規(guī)律

師：那你們能用這一知識(shí)點(diǎn)來(lái)解釋三角形的三邊關(guān)系嗎？（學(xué)生回答略）

師：如果蛋糕分別在A、B、C的位置上，螞蟻該怎么走？為什么？

生22：三角形任意兩邊長(zhǎng)度的和大于第三邊。

師：我們還可以通過(guò)舊知驗(yàn)證今天發(fā)現(xiàn)的規(guī)律。

【評(píng)析】上述教學(xué)，教師通過(guò)創(chuàng)設(shè)情境，既詳細(xì)解釋現(xiàn)象背后蘊(yùn)含的數(shù)學(xué)道理，驗(yàn)證了“三角形兩邊長(zhǎng)度的和大于第三邊”這一結(jié)論的正確性，又體0b879a42ebf371e96fa80e6a1ee0c753現(xiàn)了數(shù)學(xué)與生活之間的密切聯(lián)系，發(fā)展了學(xué)生的推理意識(shí)。

五、拓展應(yīng)用，延伸思考

1.判斷范圍

師：（出示下表）一個(gè)三角形，兩邊分別長(zhǎng)12厘米和18厘米，第三條邊的長(zhǎng)可能是多少厘米？在合適的答案下面打“√”，并說(shuō)明理由。

師：如果現(xiàn)在沒(méi)給答案選擇，你們能說(shuō)出第三條邊的長(zhǎng)可能是多少嗎？（學(xué)生紛紛提出猜測(cè)）

2.研究范圍

師：看來(lái)，第三條邊的長(zhǎng)是有范圍的，我們一起來(lái)看看吧！（幾何畫(huà)板演示第三條邊的范圍，總結(jié)得出范圍為6<x<30）在這個(gè)范圍里只能是整數(shù)嗎？小數(shù)可以嗎？（學(xué)生思考）看來(lái)，可以是任意數(shù)。

【評(píng)析】這一環(huán)節(jié)的教學(xué)，讓學(xué)生的思考有了深度和廣度，有助于學(xué)生理解與把握問(wèn)題的本質(zhì)，明確解決問(wèn)題的路徑，發(fā)展他們的幾何直觀。

六、全課總結(jié)，關(guān)聯(lián)思考

師：回顧今天的探究之旅，借助尺規(guī)作圖，我們既深入研究了三角形的三邊關(guān)系，又根據(jù)數(shù)學(xué)事實(shí)驗(yàn)證了結(jié)論，讓研究有據(jù)可證。三角形的知識(shí)還有很多，我們以后再深入學(xué)習(xí)。

【評(píng)析】教師把已學(xué)的和將學(xué)的知識(shí)融入完整的背景中讓學(xué)生去感悟，引發(fā)他們對(duì)三角形三邊關(guān)系、邊角關(guān)系的猜想，體現(xiàn)素養(yǎng)導(dǎo)向、啟智增慧的作用，為學(xué)生后續(xù)的深入學(xué)習(xí)奠基。

【總評(píng)】

“三角形的三邊關(guān)系”屬于綜合與實(shí)踐的課程內(nèi)容，具有較強(qiáng)的邏輯推理和探究性。《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2022年版）》在“三角形的三邊關(guān)系”教學(xué)中新增了尺規(guī)作圖這一內(nèi)容，旨在讓學(xué)生感受尺規(guī)作圖價(jià)值的同時(shí)，發(fā)展他們的推理意識(shí)、幾何直觀、空間觀念等素養(yǎng)。推理意識(shí)主要包括合情推理和演繹推理。合情推理是根據(jù)已知的事實(shí)、線索，大膽猜測(cè)和推測(cè)結(jié)果的過(guò)程。演繹推理通常用來(lái)驗(yàn)證合情推理得到的結(jié)論是否正確，是從一般走向特殊的思維方式。本節(jié)課教學(xué)，教師注重引導(dǎo)學(xué)生在探究中感悟規(guī)律，培養(yǎng)學(xué)生的推理意識(shí)。

一、尺規(guī)作圖，助力建構(gòu)推理平臺(tái)

推理意識(shí)的培養(yǎng)是一個(gè)緩慢的發(fā)展過(guò)程，需要通過(guò)直觀的方式來(lái)支撐。因此，借助尺規(guī)作圖進(jìn)行教學(xué)，既可以讓學(xué)生體會(huì)到圓規(guī)和直尺在作圖過(guò)程中的作用，更好地探究新知，又為接下來(lái)發(fā)展學(xué)生的推理意識(shí)提供了平臺(tái)。如果探索過(guò)程中僅單純地進(jìn)行推理說(shuō)明，就會(huì)枯燥乏味，而借助圖形觀察推理出不等式關(guān)系式，能更直觀、更科學(xué)，易于學(xué)生理解。

二、數(shù)據(jù)比較，全面凸顯推理過(guò)程

推理意識(shí)的培養(yǎng)應(yīng)貫穿整個(gè)數(shù)學(xué)教學(xué)過(guò)程，只有這樣，學(xué)生才能真正掌握推理的方法。如在方法優(yōu)化環(huán)節(jié)，教師引導(dǎo)學(xué)生尋找推理的路徑，最后得出“只需要判斷兩條較短的線段的和大于第三條線段”這一結(jié)論。整個(gè)探究過(guò)程凸顯推理的重要性，加深了學(xué)生對(duì)三角形三邊關(guān)系的理解。

三、積累經(jīng)驗(yàn)，精準(zhǔn)培養(yǎng)推理意識(shí)

課堂上，教師鼓勵(lì)并創(chuàng)造條件讓學(xué)生經(jīng)歷探究學(xué)習(xí)的過(guò)程，積累數(shù)學(xué)活動(dòng)經(jīng)驗(yàn)，培養(yǎng)學(xué)生的推理意識(shí)。如演繹推理、論證歸納環(huán)節(jié)，教師引導(dǎo)學(xué)生聯(lián)系前后知識(shí)重新思考三角形的三邊關(guān)系時(shí)，先創(chuàng)設(shè)情境，再提出問(wèn)題，使學(xué)生由此聯(lián)想到“兩點(diǎn)之間線段最短”這一知識(shí)點(diǎn)。這樣教學(xué)，點(diǎn)燃了學(xué)生的學(xué)習(xí)熱情，夯實(shí)學(xué)生的認(rèn)知基礎(chǔ)，有效培養(yǎng)了學(xué)生的推理意識(shí)。

總之，數(shù)學(xué)課堂中注重培養(yǎng)學(xué)生的推理意識(shí)，有助于學(xué)生養(yǎng)成獨(dú)立思考的良好習(xí)慣、勇于探索的科學(xué)精神。同時(shí)，學(xué)生綜合運(yùn)用推理方法，能為解決更復(fù)雜的數(shù)學(xué)問(wèn)題提供有力的工具和方法，提高自身的解決問(wèn)題能力。

［ 參 考 文 獻(xiàn) ］

[1] 江益珍，鄭愛(ài)娣.尺規(guī)“探”三邊 顯“山”又露“水”：《玩轉(zhuǎn)三角形之三邊關(guān)系》教學(xué)設(shè)計(jì)[J].小學(xué)教學(xué)設(shè)計(jì)，2024（11）：56-58.

[2] 張悅嬛.立足新課標(biāo) 探究新課堂：尺規(guī)作圖的實(shí)驗(yàn)研究[J].小學(xué)教學(xué)設(shè)計(jì)，2024（11）：48-50.

（責(zé)編 杜 華）