基于多模深度森林和迭代Kuhn-Munkres的動態上車點推薦算法

摘 要：

針對現存動態上車點配置模型在大規模算例的全局最優和求解效率方面存在瓶頸的問題，基于乘客步行距離、乘客步行時間、上車點路況指標以及至乘客目的地所需成本四個關鍵影響因子進行建模，并提出了基于多模深度森林的動態上車點預測算法和一種迭代Kuhn-Munkres上車點配置算法。預測算法融合了多模態決策樹結構和深度學習技術以提升模型預測準確性；配置算法通過多場景自適應機制自動調整邊權重并選擇最優邊進行增廣，以得到所有乘客和上車點的最優配置。實驗結果表明，相較于其他主流預測模型，該預測算法平均絕對誤差降低2.705，均方誤差降低5.915，可決系數提升0.214，解釋方差提升0.195；配置算法在乘客數量占優條件下的平均調度效果相較于實驗中其他方案提高了2.04%。這表明預測算法和配置算法具有較高的實用性，且配置算法在處理大規模實例上具有明顯優勢。

關鍵詞：上車點推薦；多模深度森林；迭代Kuhn-Munkres算法；網約車；城市交通

中圖分類號：TP301.6"" 文獻標志碼：A""" 文章編號：1001-3695（2024）12-015-3634-11

doi： 10.19734/j.issn.1001-3695.2024.04.0123

Dynamic pick-up point recommendation based on multi-modal deep forest and iterative Kuhn-Munkres algorithm

Guo Yuhan， Zhu Rushi

（School of Science/School of Big Data Science， Zhejiang University of Science amp; Technology， Hangzhou 310023， China）

Abstract：

To address the bottleneck issues of global optimality and computational efficiency in existing dynamic pick-up point allocation models for large-scale scenarios， this paper developed a model based on four key influencing factors： passenger walking distance， passenger walking time， pick-up point road conditions， and the cost to the passenger’s destination. This paper proposed a multi-modal deep forest-based dynamic pick-up point prediction algorithm and an iterative Kuhn-Munkres pick-up point allocation algorithm. The prediction algorithm integrated a multi-modal decision tree structure with deep learning techniques to enhance prediction accuracy. The allocation algorithm utilized a multi-scenario adaptive mechanism to automatically adjust edge weights and selected the optimal edges for augmentation to achieve the optimal allocation for all passengers and pick-up points. Experimental results demonstrate that the proposed prediction algorithm reduces the mean absolute error by 2.705， the mean squared error by 5.915， increases the coefficient of determination by 0.214， and improves the explained variance by 0.195 compared to other mainstream prediction models. Under conditions where passenger quantity advantage， the allocation algorithm improves average scheduling effectiveness by 2.04% compared to other schemes tested in the experiments. These results indicate that the proposed algorithms are highly practical， with the allocation algorithm shows significant advantages in handling large-scale instances.

Key words：pick-up point recommendation; multi-modal deep forest; iterative Kuhn-Munkres algorithm; online ride-hailing; urban transportation

0 引言

近年來，智能通信終端的普及為乘客和網約車司機間的信息交流提供了便捷性和即時性，消除了以往由于空間差異而存在的信息壁壘［1］。在乘客通過智能軟件發起訂單并與司機匹配后，雙方均需前往指定的上車點，合理的上車點配置可有效提升接駕效率、降低服務的經濟和時間成本且有助于緩解交通擁堵。

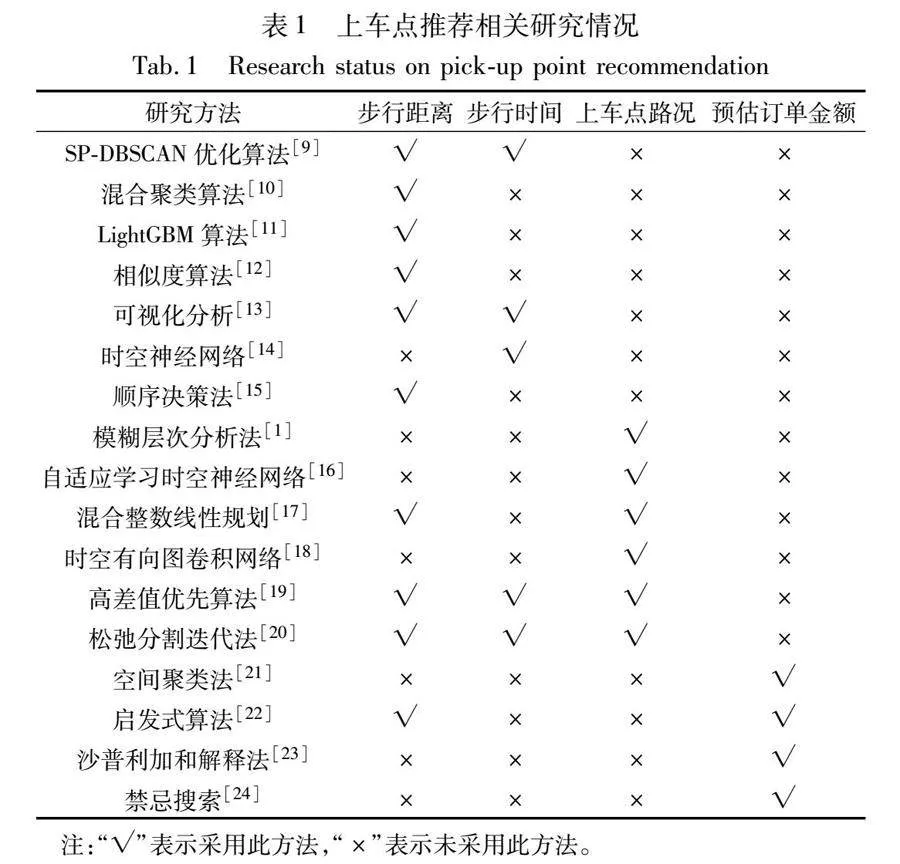
目前國內外對于網約車的研究主要集中在需求預測［2，3］、匹配調度［4］以及路徑規劃［5，6］等方面，對于上車點推薦的研究較為有限。文獻［7，8］對上車點推薦問題進行了綜述，將其研究方向主要歸納為減少乘客的步行距離和步行時間［9～15］，優化上車點路況［1，16～20］和降低出行成本［21～24］等方面。

a）在減少乘客的步行距離和步行時間方面， Xia等人［9］設計了基于Spark的并行SP-DBSCAN算法，以滿足乘客在特定位置沒有成功搭車而隨機轉向下一個地點時仍能在熱點區域乘車的要求。Mann等人［10］基于劃分聚類法和層次聚類法提出了改進的混合聚類算法，向乘客推薦距離當前位置最近的上車點。康軍等人［11］對各個上車點出租車空載率進行預測，并推薦乘客去往空載率最高且最近的上車點候車。Olakanmi等人［12］基于司機與乘客曾訪問過的歷史位置提出了一種考慮司機和乘客間信任與評價相似度的模型，為乘客推薦最短步行距離的上車點；Gu等人［13］設計了一個可視化分析系統，旨在可視化探索乘客在不同區域選擇對自身有利的上車點；You等人［14］基于粒度網格和時空神經網絡可有效預測和優化乘客步行時間和等待時間；Dieter等人［15］根據將乘客分配至上車點問題建模為一個順序決策過程，以最小化乘客的步行距離。

b）在優化上車點路況方面，Zhu等人［1］綜合各種交通影響因素，在保證上車點設置與實際交通情況相適應的情況下為乘客推薦上車點。Chang等人［16］基于上車點路況指標進行上車點推薦，并設計了宏觀路徑推薦方法，旨在提升交通領域低碳管理水平。Aliari等人［17］以乘客步行距離為指標，利用混合整數線性規劃為乘客推薦上車點，以此緩解上車點擁堵問題。Zhang等人［18］根據歷史上下車數據進行建模，利用時空有向圖卷積網絡算法為乘客推薦路況良好的上車點。郭羽含等人［19］建立上車點的復合收益評價體系，構建了上車點的動態推薦模型；在此基礎上，他們設計了多目標整數規劃模型，并提出了松弛分割迭代算法，從不同角度對上車點進行有效推薦［20］。

c）在降低出行成本方面，文獻［21］利用空間聚類方法在空間和時間尺度上合并出租車行程簇，生成使乘客和出租車公司出行成本最小的上車點；文獻［22］設計了一種基于用戶激勵機制的上車點推薦系統，鼓勵乘客在一定距離內步行至合適的上車點，以最大限度降低出行成本；文獻［23］發現出行成本與乘客使用乘車服務軟件具有明顯的非線性關系；文獻［24］提出了網約車與乘客最佳乘車匹配的禁忌搜索，使乘客可節約更多成本，最大限度地提高乘客和司機的利益。

表1對現存代表性研究進行了總結，分析了各研究對步行距離、步行時間、上車點路況、預估訂單金額等主要指標的考慮情況。

綜合來看，現存模型與方法考慮的影響因素較為單一，滴滴出行在統計并分析網約車數據后發現，乘客出行行為與成本、時間、路況、便利度等多種因素相關。Vega-Gonzalo等人［25］通過問卷調查及廣義結構方程模型得出乘客打車頻率不僅受出行成本影響，還受行車安全、步行距離等因素的影響。Hou等人［26］認為空間可達性及路況是影響乘客出行的關鍵因素。Naumov等人［27］通過對乘客的出行習慣進行仿真分析，發現減少步行距離可提升約25%的乘客滿意度。由此可見，綜合分析乘客出行影響因素對于準確合理推薦上車點具有重要意義。此外，現存研究還存在以下問題需進一步解決：a）現存研究主要基于GPS數據進行分析，但由于GPS數據所跟蹤的坐標點與實際可行的上車位置間存在差異，準確提取潛在上車點仍具挑戰性；b）匹配算法僅獨立考慮單次推薦，未將全局最優作為優化目標，導致同時段內單一上車點訂單積壓，從而引發訂單取消或交通擁堵等問題。

針對上述問題，本文建立了考慮多影響因子的上車點推薦模型，提出了基于多模深度森林的動態上車點預測算法，并基于其預測結果設計了一種迭代Kuhn-Munkres上車點配置算法，實現了多角度多策略的上車點動態配置。本文主要貢獻包括四個方面：

a）提出了基于路網匹配的潛在上車點提取方法，通過綜合考量道路條件、實時交通信息等因素充分整合路網信息，使得所提取的潛在上車點更具實時性和準確性。

b）基于乘客步行距離、步行時間、上車點路況指標和預估訂單金額四個關鍵影響因子建立上車點推薦模型，構建了全面考慮乘客便利性、運營效率及經濟可行性的模型。

c）提出了基于多模深度森林的動態上車點預測算法，融合了不同結構的決策樹，利用多模隨機森林和復合隨機森林替代原始隨機森林和完全隨機森林，對經過滑動窗口掃描后的子樣本進行多模態特征采樣，并通過級聯結構將采樣后的特征逐層組織和整合，有效降低了過擬合風險，提高了模型的泛化能力。

d）設計了一種高效的迭代Kuhn-Munkres上車點全局最優配置算法，在每輪迭代中通過多場景自適應機制自動調整乘客與上車點之間的邊權重，并選擇最優邊進行增廣以持續優化配置結果，從而顯著提升配置算法的平均調度效果，并在大規模算例上具有較高的求解效率。

1 問題定義與建模

1.1 問題定義

1.2 數學模型

本文基于乘客步行距離、步行時間、上車點路況指標和預估訂單金額四個關鍵影響因子建立上車點推薦模型。首先，乘客步行距離和時間直接關聯乘客體驗及出行效率，合理的步行距離和時間既可鼓勵乘客接受一定程度的步行以達到更高效的車輛分配（如減少空駛、縮短等待時間），又避免造成乘客不便，從而提高整體服務滿意度。在城市密集區域，限制過長的步行距離對于促進公共交通與網約車的無縫銜接尤為重要。其次，考慮到城市交通擁堵狀況的普遍性，上車點路況直接影響接駕效率和行程時間預測的準確性。將路況納入模型，可避免在交通繁忙或道路施工區域安排上車點，減少延誤，同時優化司機的行駛路徑以提高整體運營效率并降低碳排放。最后，成本因素不僅關乎乘客支付意愿，也是平臺和司機收益考量的關鍵，合理優化成本有助于平衡供需雙方利益，促進資源的高效配置，避免因成本過高導致的服務不可持續問題。

針對上述指標，本文建立了線性整數規劃模型，將多個指標通過線性加權組合為單目標函數，從而將多指標優化問題轉換為該目標函數最大化問題。乘客與上車點配置階段以多指標線性加權和作為評價乘客與上車點的匹配價值，再將其轉換為一個帶約束的二分圖匹配問題。問題目標即為求得一種配置方案，使得所有乘客上車點匹配對的價值總和最大，因此可將該問題的目標函數定義為式（8）。

其中：coij表示乘客pj是否在上車點bi上車。式（8）中α、δ、γ、φ分別為TRCIbi、WDISbipj、TIMEpj、COSTbipj在目標函數中的權重參數。式（9）表示對分配至上車點bi的乘客數進行限制，確保其不超過設定的閾值bi。式（10）表示一個乘客只可被分配至一個特定的上車點上車。式（11）限定了coij的取值范圍，其中1表示上車，0表示不上車。

根據上述定義構造了適用于動態上車點預測的數據集U4×m={（xj，yj）}mj=1，其中xj=（TRCIbi、WDISbipj、TIMEpj、COSTbipj）T為上述定義的4維特征向量，yj∈{0，1}表示經過歸一化處理后的動態上車點得分，得分越高代表該上車點更具推薦價值。

本文模型屬NP-hard問題，當解空間巨大時，整數約束使問題的求解難度顯著提升，在最壞情況下求解時間隨問題規模呈指數增長。二分圖匹配問題盡管存在多項式時間算法來解決完美匹配問題，但在大規模數據集上，算法計算復雜度依然較高。尤其當二分圖的節點數量巨大時，模型求解的復雜度和資源需求急劇上升。此外，上車點推薦過程具有實時性，需在匹配過程中實施快速決策，對模型求解效率提出了較高要求。

2 求解算法

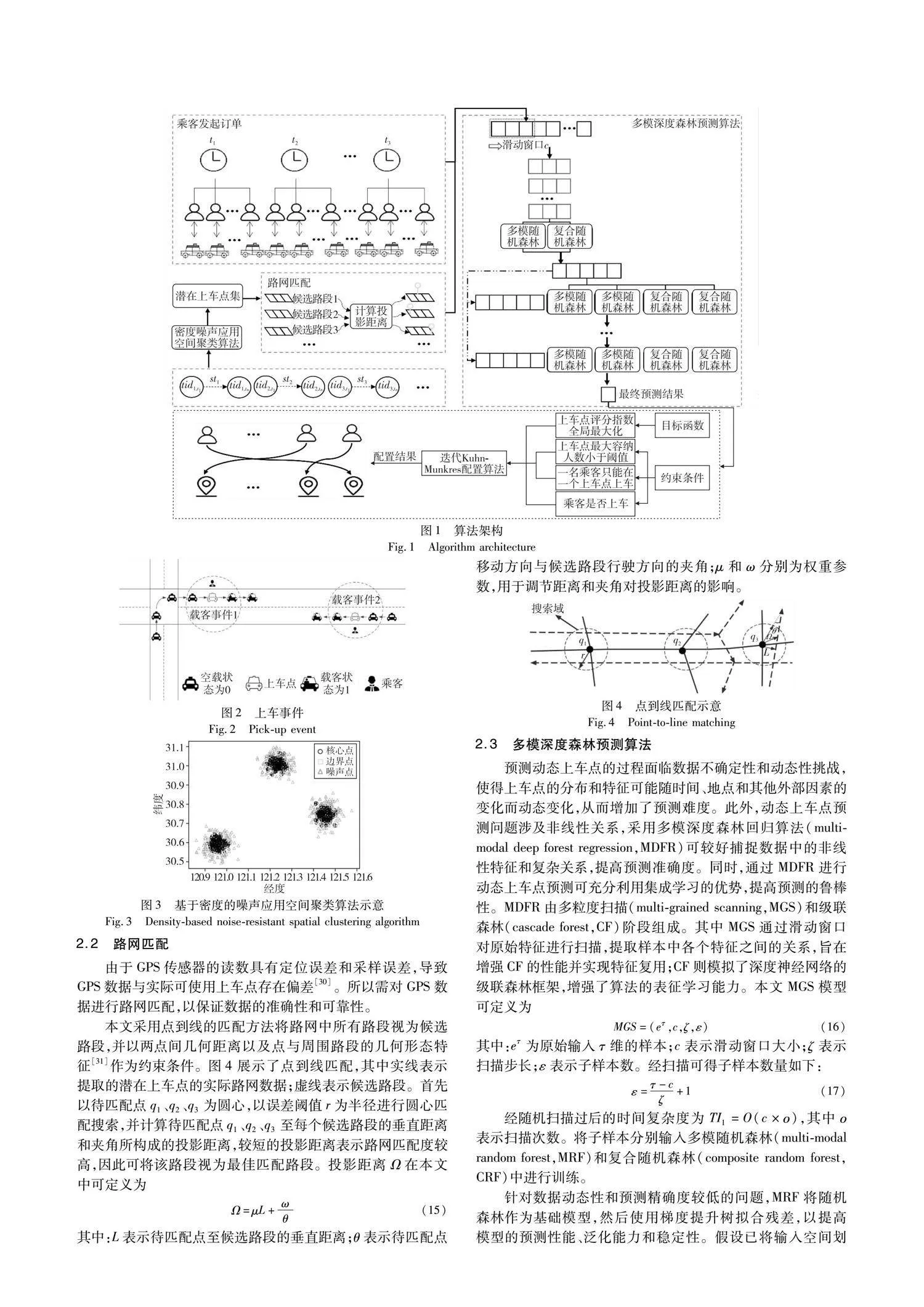
針對模型特點，本文提出了多模深度森林動態上車點預測算法與迭代Kuhn-Munkres上車點配置算法，其總體架構如圖1所示。a）通過潛在上車點提取算法，在預測前對上車點集合進行數據處理并篩選出潛在上車點，保障后續預測和配置過程中數據的準確性和真實性；b）通過點到線匹配算法將經過篩選的潛在上車點與真實路網中的路段匹配，解決GPS數據所跟蹤的坐標點與實際可行上車位置間存在差異的問題；c）通過多模深度森林預測算法，利用1.2節中建立的特征向量與上車點得分，構建用于模型訓練的訓練集和用于校驗的測試集，并輸出可用于上車點推薦的預測結果；d）針對動態上車點的全局最優化問題，設計了迭代Kuhn-Munkres上車點配置算法，利用預測結果進行決策，通過多場景自適應機制持續優化權重參數和配置結果，使其更好地適應不同策略下的配置需求，從而實現乘客與上車點的全局供需平衡。

2.1 潛在上車點提取

在GPS數據中，軌跡點載客狀態可定義

stk=1 "網約車處于載客狀態0 "網約車處于空載狀態（12）

通過觀察圖2上車事件圖中載客事件1，可確定當軌跡點載客狀態由0轉換為1時，即發生了一次上車事件，此時將載客狀態為1的數據點視為一個上車點。

根據GPS數據中網約車在相鄰兩個時刻軌跡點載客狀態的變化，可提取出網約車的候選上車點集Htk，再對所有車輛的候選上車點進行合并得集合D，如式（13）（14）所示。

Htk=［tidk，stk|tidkk，t（stk）=1 amp; tidkk，t－1（stk）=0］（13）

D={Ht1∪Ht2∪…∪Htk∪…∪Hts}（14）

最后，利用基于密度的噪聲應用空間聚類算法將集合D以半徑為Eps、密度閾值為MinPts進行聚類，得到潛在上車點集B。算法示意如圖3所示。

2.2 路網匹配

由于GPS傳感器的讀數具有定位誤差和采樣誤差，導致GPS數據與實際可使用上車點存在偏差［30］。所以需對GPS數據進行路網匹配，以保證數據的準確性和可靠性。

本文采用點到線的匹配方法將路網中所有路段視為候選路段，并以兩點間幾何距離以及點與周圍路段的幾何形態特征［31］作為約束條件。圖4展示了點到線匹配，其中實線表示提取的潛在上車點的實際路網數據；虛線表示候選路段。首先以待匹配點q1、q2、q3為圓心，以誤差閾值r為半徑進行圓心匹配搜索，并計算待匹配點q1、q2、q3至每個候選路段的垂直距離和夾角所構成的投影距離，較短的投影距離表示路網匹配度較高，因此可將該路段視為最佳匹配路段。投影距離Ω在本文中可定義為

Ω=μL+ωθ（15）

其中：L表示待匹配點至候選路段的垂直距離；θ表示待匹配點移動方向與候選路段行駛方向的夾角；μ和ω分別為權重參數，用于調節距離和夾角對投影距離的影響。

2.3 多模深度森林預測算法

預測動態上車點的過程面臨數據不確定性和動態性挑戰，使得上車點的分布和特征可能隨時間、地點和其他外部因素的變化而動態變化，從而增加了預測難度。此外，動態上車點預測問題涉及非線性關系，采用多模深度森林回歸算法（multi-modal deep forest regression，MDFR）可較好捕捉數據中的非線性特征和復雜關系，提高預測準確度。同時，通過MDFR進行動態上車點預測可充分利用集成學習的優勢，提高預測的魯棒性。MDFR由多粒度掃描（multi-grained scanning，MGS）和級聯森林（cascade forest，CF）階段組成。其中MGS通過滑動窗口對原始特征進行掃描，提取樣本中各個特征之間的關系，旨在增強CF的性能并實現特征復用；CF則模擬了深度神經網絡的級聯森林框架，增強了算法的表征學習能力。本文MGS模型可定義為

MGS=（eτ，c，ζ，ε）（16）

其中：eτ為原始輸入τ維的樣本；c表示滑動窗口大小；ζ表示掃描步長；ε表示子樣本數。經掃描可得子樣本數量如下：

ε=τ－cζ+1（17）

經隨機掃描過后的時間復雜度為TI1=O（c×ο），其中ο表示掃描次數。將子樣本分別輸入多模隨機森林（multi-modal random forest，MRF）和復合隨機森林（composite random forest，CRF）中進行訓練。

針對數據動態性和預測精確度較低的問題，MRF將隨機森林作為基礎模型，然后使用梯度提升樹擬合殘差，以提高模型的預測性能、泛化能力和穩定性。假設已將輸入空間劃分為U個單元，且在每個單元上有固定輸出值，則決策樹模型可定義為

f（xl）=∑Ul=1ulI（xl∈Ul）（18）

利用多棵決策樹集成隨機森林，計算初始預測值與真實標簽之間的殘差，如式（20）所示。

f^（xl）=∑Ul=1f（xl）U（19）

υl=f（xl）－f^（xl）（20）

將殘差作為新的目標值，利用梯度提升樹擬合殘差，梯度提升樹在本文可定義為

MRF（xl）=∑Ul=1ηlf（xl）（21）

其中：ηl表示第l棵決策樹的權重。梯度提升樹采用梯度下降法來求解最優模型，對于第ι輪迭代，MRF可定義為

MRFι（xl）=MRFι－1－ηι∑Ul=1ΔFL（yl，MRFι－1（xl）+υl）（22）

最后，重復上述步驟多次，直到達到最小殘差為止。

整個過程中需要對殘差進行循環擬合以達到最小，時間復雜度為TI2=O（4m×log m×U+4m×ι）。

針對動態上車點預測的非線性特征和復雜關系問題，CRF將多項式特征變換嵌入到決策樹算法中以增強決策樹的非線性建模能力。在節點分裂過程中對輸入的子樣本進行多項式特征變換，形成新的特征集合如式（24）所示。

xj=（1，xj1，…，xj4，x2j1，…，x2j4，…，xκj1，…，xκj4）（23）

Xj=（x1，x2，…，xj，…，xm）（24）

式（23）中，xκj4表示第j個數據第4維特征的第κ階多項式。將特征集合利用平方誤差最小化準則作為劃分節點的條件［32］，則CRF可以定義為

CRF（Xj）=minj（∑Xj∈U（yj－f（Xj））2）（25）

此過程中無循環，僅為決策樹節點的分裂，時間復雜度為TI3=O（4κm×log m）。

圖5中多粒度掃描階段展示了MGS生成CF輸入特征向量的過程。首先將4 dim的xj=（TRCIbi，WDISbipj，TIMEpj，COSTbipj）T作為輸入層，滑動窗口c大小分別取1 dim、2 dim和3 dim，對輸入樣本進行滑動取樣；掃描步長ζ默認為1，分別得子樣本數ε為4、3和2。然后采用MRF和CRF對所得子樣本進行訓練，每個樣本輸出1個2 dim的概率特征向量，即分別生成16 dim，12 dim和8 dim的特征向量。最后，將所有向量合并作為CF輸入特征向量。

在CF中，MGS的輸出結果MGSo作為第一層輸入CFx1，特征向量FV作為第一層輸出CFy1，前層輸入和輸出結果合并作為下一層的輸入［33］，第一層輸出和第二層輸入可分別定義為

CFy1=g（1）（MGSo，FV）（26）

CFx2={MGSo∪FV∪CFy1}（27）

式（26）中g（1）表示第一層CF中的特征處理函數。每層輸入均來自于上層的特征處理，并將經過處理的特征傳遞給下層，因此第M層輸出和第M+1層輸入可分別定義為

CFyM=g（I）（CFxM）（28）

CFxM+1={MGSo∪FV∪CFy1∪CFyM}（29）

式（28）中g（I）表示第I層CF中的特征處理函數。在CF中，每個森林預測樣本xJ的輸出類向量和輸出結果，可分別定義為

G（xJ）=∑VJ=1（MRF（xJ）+CRF（xJ）+CFxJ）V（30）

W（xJ）=G11（xJ）G12（xJ）…G1N（xJ）

G21（xJ）G22（xJ）…G2N（xJ）

GK1（xJ）GK2（xJ）…GKN（xJ）（31）

其中：V表示森林中決策樹個數；GKN（xJ）表示CF中第N層第K個森林所輸出的預測向量。根據預測向量對樣本進行最終預測，如式（32）所示。

CF（xJ）=max（avg（W（xJ）））（32）

CF過程中每層為上一層的結果處理，無循環，時間復雜度為TI4=O（m×K×U×N/）+O（4m+），其中表示每個森林可以劃分為個子森林。綜上所述，多模深度森林的時間復雜度為TI=TI1+TI2+TI3+TI4。

圖5中級聯森林階段展示了CF的完整流程，經過MGS后，共提取了36 dim特征向量作為CF的第一層輸入；第一層經過MRF和CRF訓練后產生8 dim的增加特征向量，加之原始36 dim特征向量，形成44 dim變換特征向量作為第二層輸入。依此類推，經過N層處理后輸出為每個MRF或CRF對動態上車點的預測評分。最后，對該結果的平均取最大值，即可得最終上車點評分。

2.4 迭代Kuhn-Munkres上車點配置算法

在乘客和上車點的動態配置問題中，首先需構建帶權二分圖，利用乘客對上車點的評分作為邊權重；然后采用二分圖最大權匹配算法求出最優匹配方案，并計算匹配后子圖中所有邊權重的和［34］。由于實際路網數量龐大，傳統二分圖最大權匹配算法（Kuhn-Munkres， KM）在處理大型算例時表現出較高的時間復雜度，且其運行時間呈現出超線性趨勢增長［35］，因此，同時規劃出乘客和任一上車點之間配置策略的難度較高，無法保證算法的實時性；此外，KM算法只能解決一對一的匹配問題，無法有效處理一對多的匹配問題。基于上述考慮，本文提出了迭代Kuhn-Munkres上車點配置算法（iterative Kuhn-Munkres， IKM），其能在較短時間內搜索到較優的配置結果，并可結合實際情況靈活調整路徑、切換配置頂點，以實現乘客與上車點的全局供需平衡。在每輪迭代中針對局部增廣路徑進行更新，且在無法找到更多增廣路徑時提前停止迭代，從而減少了計算時間，提高了算法的效率。IKM算法偽代碼如算法1所示。

算法1 IKM算法

輸入：OBP=（B，P，（i， j）），bi，yj。

輸出：最優匹配結果。

mate= {}；

bi=max{yj}， pj=0，mai=0，Oau={}; /*初始化節點和上車點節點人數*/

for pj in P

max（（i， j））=－∞;

bei=;

/*初始化賦權值和最佳上車點*/

for bi in B

if bi+pj=（i， j）

if bi not in Oau

"Oau［bi］=［］;

Oau［bi］.append（pj）;

/*對于每個乘客節點j，都能在輔助二分圖中找到對應的可行上車點節點集合*/

end if

Qi={};

for bi in Oau

if len（Oau［bi］）gt;0

Qi［i］=Oau［bi］［i］;

Qi.append（Qi［i］）;

/*任取輔助二分圖中的任一匹配*/

end if

if len（Qi）==len（OBP）

mate［j］=bpj;

elseif mai≤bi

（i， j）=yj;

if （i， j）gt;max（（i， j））

max（（i， j））=（i， j）;

bei=i;

/*找到與乘客節點j權值最高的上車點節點i*/

end if

end if

if bei≠

"將乘客節點j分配給最佳上車點;

mai+=1

/*最佳上車點的容納人數增加*/

end if

if maigt;bi

將該上車點從集合B中移除;

end if

end for

end if

end for

mate［j］= 分配給乘客節點j的上車點;

mate. append（mate［j］）;

return mate;

end for

令B=∪ni=1bi，P=∪mj=1pj，可將乘客與上車點的配置問題定義為有向帶權二分圖OBP=（B，P，（i， j）），其中（i， j）表示將集合P中乘客節點j配對至集合B中上車點的權值。在此基礎上利用IKM通過多場景自適應機制進行配置，其具體步驟如下。

首先輸入二分圖OBP=（B，P，（i， j）），根據式（8）設置初始節點標號bi=max{yj}，pj=0，mai=0。

從OBP中選擇滿足條件bi+pj=（i， j）的邊構造輔助二分圖Oau，并任取Oau的一個匹配Qi。若Qi飽和了OBP的所有節點，那么Qi即為所求最優匹配，計算停止并返回匹配結果，即mate［j］=bpj，其中bpj表示分配給乘客節點j的上車點；否則，根據式（1）可分別得式（33）（34）。

（i， j）=yj" mai≤bi0其他 （33）

bei=i，max（（i， j））=（i， j） （i， j）gt;max（（i， j））其他（34）

若此時bei≠，則將pj分配至bei，最佳上車點的容納人數相應增加。當最佳上車點人數大于該上車點人數容量閾值bi時，將該最佳上車點bei從上車點集合B中移除。

最后，尋找一條由集合P到集合B的增廣路徑ρ，令Qi+1=Qi⊕ρ，i=i+1。重復以上步驟，直至Qi飽和了OBP的所有節點。

設配置圖中的節點數量為mnode，邊數量為medge，乘客數量為m，上車點數量為n。對于原算法，單次KM算法進行乘客與上車點配置的時間復雜度為O（mnode×medge），需要執行mnode次，故總體時間復雜度為O（m2node×medge）。而經過IKM算法迭代縮減循環，實際總體執行IKM算法的次數為min（m，n），故時間復雜度為O（mnode×medge×min（m，n））。需要強調的是，以上處理并未增加空間開銷。

3 實驗與分析

實驗采用Python語言，相關數據來源于上海市出租車GPS數據集以及滴滴出行中上海市網約車訂單數據，實驗參數設置如表2所示。由于本文所使用的數據集基于上海市出租車數據集，所以按照上海市的交通標準設定定價方案。

本文權重參數基于層次分析法，并綜合考慮真實應用場景與大量實驗的最優輸出值進行設定［36］。首先根據影響因子構造判斷矩陣A，然后由判斷矩陣A計算出被比較的影響因子對于該準則的相對權重并進行一致性檢驗。利用一致性指標CI和一致性比例CR判斷一致性檢驗是否通過，一致性指標CI和一致性比例CR可分別定義為

CI=λmax（A）－－1（35）

CR=CIRI（36）

其中：λmax（A）表示判斷矩陣A的最大特征值；表示判斷矩陣A的維數；RI表示判斷矩陣A的一致性標準。當CR≤0.1時，表明判斷矩陣A的一致性程度在容許范圍內，此時可對判斷矩陣A采用算術平均法、幾何平均法、特征值法三種方法所得的權重計算平均值，避免單一方法所產生的偏差。

3.1 預測算法評估

本文采用平均絕對誤差（MAE）、均方根誤差（RMSE）、可決系數（R2）和可解釋方差（EV）對MDFR進行評估，計算公式如下：

MAE=∑ni=1|yi－i|n（37）

RMSE=∑ni=1（yi－i）2n（38）

R2=1－∑ni=1（yi－i）2∑ni=1（yi－i）2（39）

EV=1－∑ni=1［（yi－i）－（yi－i）］2∑ni=1（yi－）2（40）

=∑ni=1yin（41）

其中：yi和i分別為觀測值和預測值；（yi－i）是（yi－i）的均值；n為觀測樣本的大小。

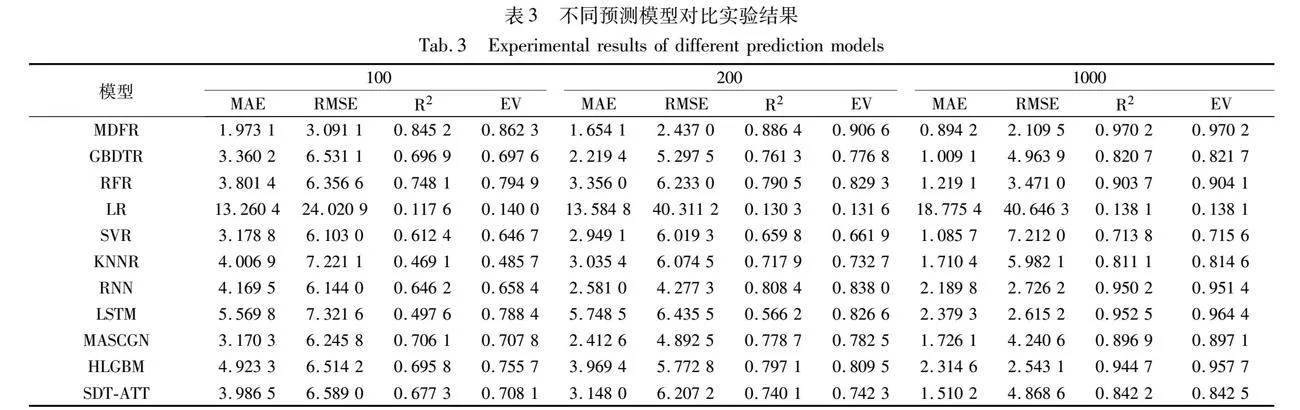
對比模型選取了：a）集成模型，梯度提升樹回歸模型（GBDTR）和隨機森林回歸模型（RFR）；b）機器學習模型，線性回歸模型（LR）、支持向量機回歸模型（SVR）和K近鄰回歸模型（KNNR）；c）代表性深度學習模型，包括循環神經網絡（RNN）和長短時記憶神經網絡（LSTM）；d）其他，多頭注意力時空卷積圖網絡模型（MASCGN）［37］、LightGBM混合模型（HLGBM）［38］和多元交互注意力機制模型（SDT-ATT）［39］。預測模型對比實驗結果如表3所示。

由表3可知，對于MDFR，其MAE、RMSE、R2和EV值平均分別為2.375、30.935、0.909以及0.911。與其他模型相比，MDFR的平均絕對誤差降低了2.705，均方誤差降低了5.915，可決系數提升了0.214，解釋方差提升了0.195，說明MDFR在預測最佳上車點方面表現良好。此外，不同模型在不同尺寸數據集上的表現存在差異，隨著數據集尺寸的增加，模型的擬合程度有所提升。但在所有模型中LR表現最差，說明線性模型無法準確預測最佳上車點，與實際情況相符。

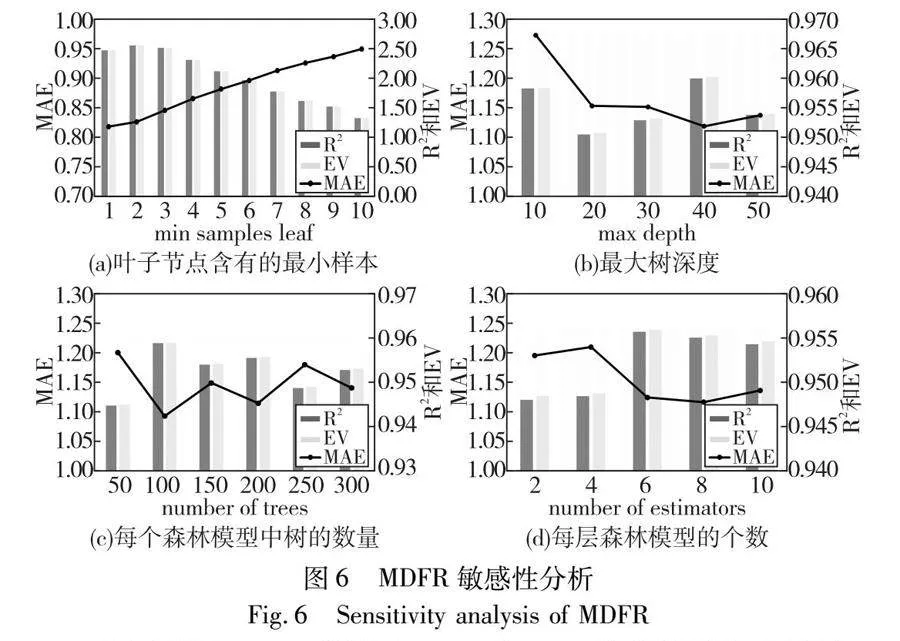
下面對MDFR進行敏感性分析，實驗中分別修改了MDFR的四個參數，即葉子節點中含有的最小樣本、最大樹深度、每個森林模型中樹的數量以及每層森林模型的個數。由圖6可知，隨著葉子節點中含有的最小樣本的增加，MAE持續上升，而R2和EV值先上升后持續下降；當最大樹深度增加時，MAE先大幅減少后趨于平穩，而R2和EV值則先減少后增大再減少；隨著每個森林模型中樹的數量增加，MAE先大幅下降后緩慢增加，而R2和EV則相反；隨著每層森林模型的個數增加，MAE、R2和EV均先增加后下降。在葉子節點含有的最小樣本小于3、最大樹深度為40、每個森林模型中樹的數量為100以及每層森林模型的個數在6～10時，MDFR表現最佳。

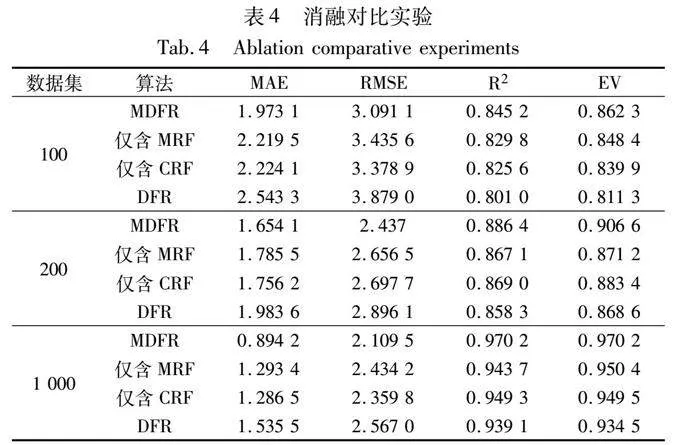
為了驗證MDFR算法中MRF和CRF的高效性和有效性，本文使用深度森林預測模型（DFR）作為基礎模型在原數據集上進行消融實驗。為了保證結果的可靠性，在隨機選擇不同尺寸的數據集上各運行10次，取10次的平均值作為最終結果。實驗結果如表4所示。

由表4可知，MDFR算法中MRF和CRF對算法MAE、RMSE、R2和EV的影響有所不同，但均比基礎模型有所提升。當處理不同尺寸大小的數據集時，MDFR、僅含MRF和僅含CRF算法比不使用這些算法的DFR， MAE分別降低了0.514、0.255和0.265；RMSE分別降低了0.568、0.272和0.302； R2分別提升了0.034、0.014和0.019，EV分別提升了0.042、0.019和0.022。產生這樣結果的原因是，MRF結合了隨機森林和梯度提升樹的優點，在每輪迭代中都會捕捉前一輪模型無法解釋的數據動態性，能夠逐步減少預測誤差，持續優化模型性能，提高模型的預測準確性；CRF則是通過在決策樹中引入多項式特征變換生成新的特征，使得模型可在更細致的層次上進行數據劃分。由于特征空間變得更復雜，決策樹可在多維空間中找到更合適的劃分點，更好地適應數據中的非線性關系和復雜性。

綜上所述，MDFR算法在大數據環境下具有良好的可行性和有效性。

3.2 配置算法評估

3.2.1 配置算法實驗結果

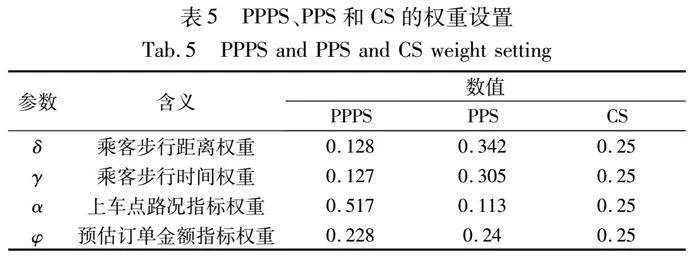
本節從乘客數量和上車點數量兩個角度，對比分析在乘客數量占優（passenger quantity advantage，PQA）和上車點數量占優（pick-up point quantity advantage，PPQA）的條件下，上車點優先策略（pick-up point priority strategy，PPPS）［1］、乘客優先策略（passenger priority strategy，PPS）［19］和本文策略（comprehensive strategy，CS）的優劣以及對動態上車點推薦的影響。PPPS［1］、PPS［19］及CS策略的參數權重設置分別如表5所示。

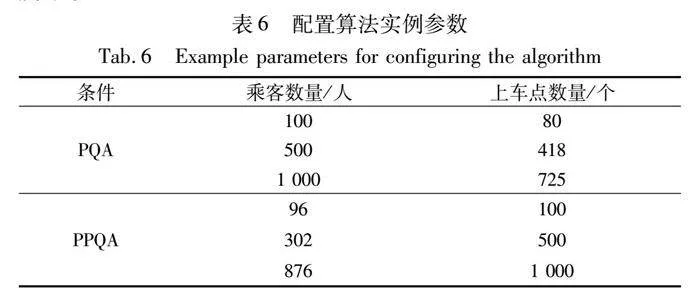
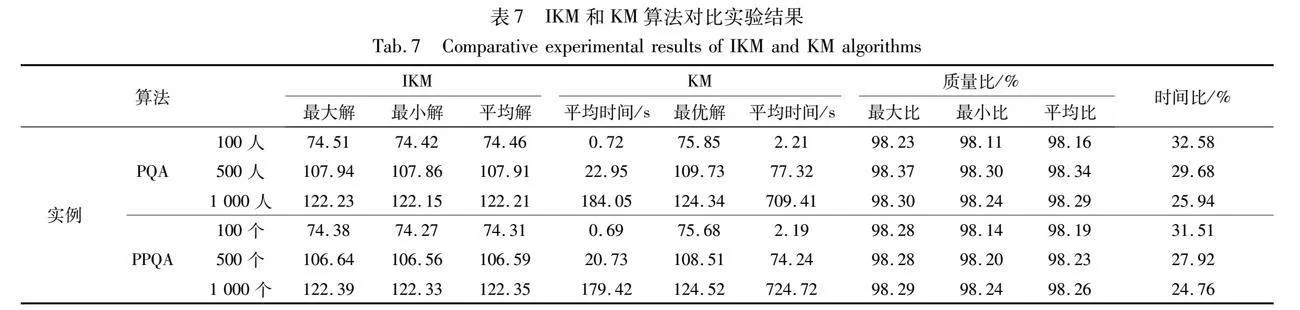
本節模擬了6個實例，3個不同數量乘客和3個不同數量上車點，實例參數如表6所示。對6個實例分別用IKM和KM算法各執行10次，將IKM的平均解、平均時間與KM算法的最優解、平均時間作比較，得到質量比和時間比，對比結果如表7所示。

由表7可知，對于較大規模的實例，時間比隨著數據集尺寸的增加逐漸下降，且質量比均在98%以上，說明與KM算法最優解相比較，IKM算法可在較短時間內得到高質量的解。IKM算法的平均運行時間緩慢增長，而KM算法的平均運行時間呈非線性增長且增長迅速，說明IKM算法的時間效率優于KM算法。

IKM和KM算法在處理PQA條件下不同規模算例數據集時的平均運行時間分別為69.24 s和238.26 s，前者僅為后者的29.06%；IKM和KM算法在處理PPQA條件下不同規模算例數據集時的平均運行時間分別為66.95 s和200.78 s，前者僅為后者的33.34%。在本實驗規模算例下，改進后的Kuhn-Munkres算法在解決乘客與上車點配置問題時表現出較好的結果，各種方案中IKM算法的求解效率是傳統KM算法的64.97%。

3.2.2 PQA條件

在某些特定時間段、特殊事件期間或交通管制時，會出現在同一時刻內乘客叫車數量大于上車點數量的情況。本條件下限定乘客數量分別為100人、500人和1 000人，而上車點數量則分別在小于100個、500個和1 000個數據集中隨機選擇不同數量的上車點進行實驗，實驗結果如表8所示。

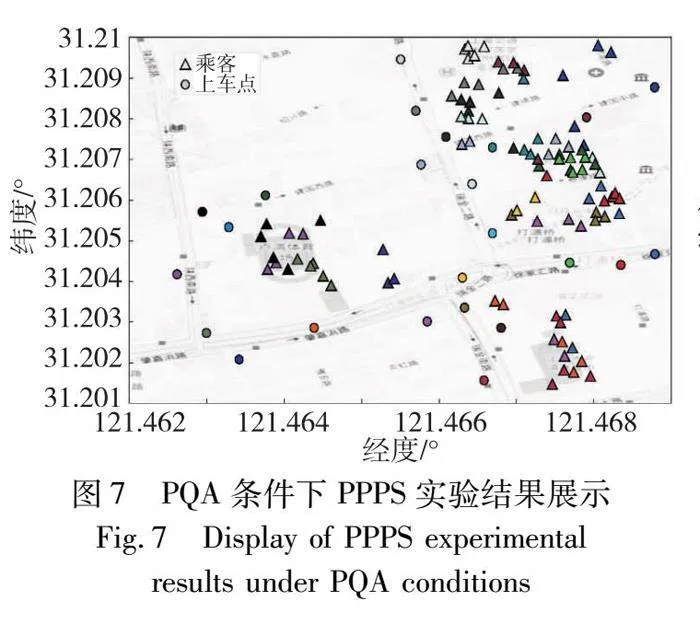
1）PPPS實驗分析

圖7中三角形圖標表示乘客，圓形圖標表示上車點，相同顏色表示該乘客被分配至該上車點（參見電子版）。盡管PPPS算法能確保每位乘客被成功配置到上車點，但應用上車點優先策略后，圖7顯示多數乘客步行距離和步行時間均有所增加。與CS和PPS相比，PPPS的平均得分分別降低了2.04%和1.08%，如表8所示。這一差異表明，在乘客與上車點的配置過程中，PPPS策略以犧牲乘客便利性為代價，追求其他目標的實現。因此，在特定PQA條件下PPPS不是最優選擇。

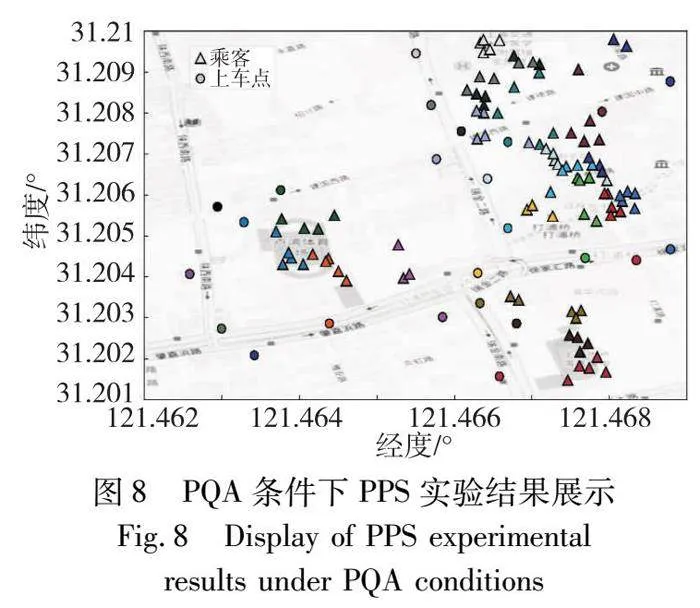
2）PPS實驗分析

圖8采用了與圖7相同的表達方法展示乘客與上車點的對應關系。PPS算法基于自適應機制，綜合考慮了乘客步行距離和步行時間，旨在為每位乘客分配一個具有相對優勢的上車點。然而，此方法在特定區域（如景點和醫院周邊）的高峰時段易引發上車點附近路況惡化現象。此外，由于司機前往乘客指定的上車點過程中發生了行程偏移，導致乘客抵達目的地的訂單金額超出預期。這些因素的共同作用使PPS的平均得分相較CS偏低，如表8所示。

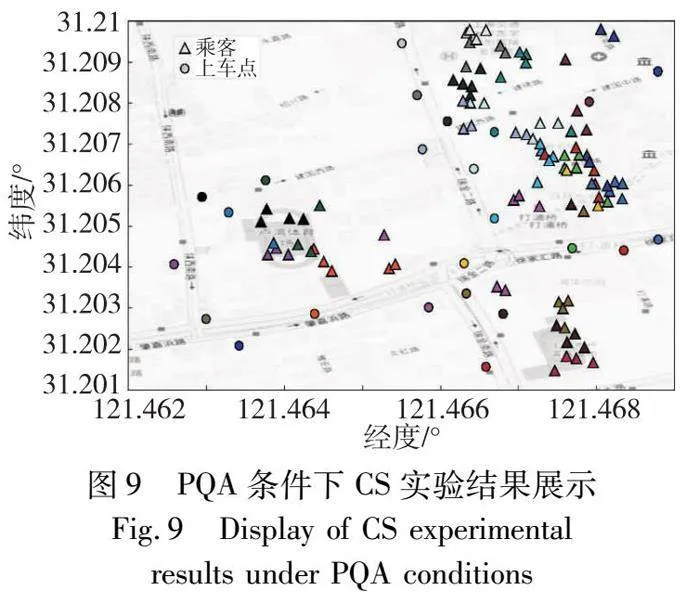
3）CS實驗分析

圖9中乘客與上車點的對應關系延續了圖7相同的表達方式。由圖9可知，CS算法通過多場景自適應機制，綜合考量了上車點路況指標、預估訂單金額、乘客步行距離及步行時間，將乘客分配至相應的上車點。盡管部分乘客被分配至距離稍遠的上車點，但并未對整體評分產生顯著影響。相反，由于所分配上車點位于交通狀況較佳的區域，且減少了不必要的路線偏離。所以，乘客到達目的地的預估金額相對較低，反映了IKM算法在綜合考量多因素后得出的優化結果。

3.2.3 PPQA條件

一般情況下，上車點數量通常會超過同時叫車的乘客數量。隨著可供選擇的上車點數量增加，乘客更易按照個人偏好選擇上車點，這也與實驗結果保持一致。通過對比分析表8和9可知，在PPQA條件下，乘客對各上車點的評分普遍高于PQA條件下的評分。本實驗設定了不同數量上車點（100個、500個和1 000個）和乘客（小于100人、500人和1 000人），并在處理好的數據集中隨機選擇各種數量的乘客經緯度以及目的地經緯度，實驗結果如表9所示。

1）PPPS實驗分析

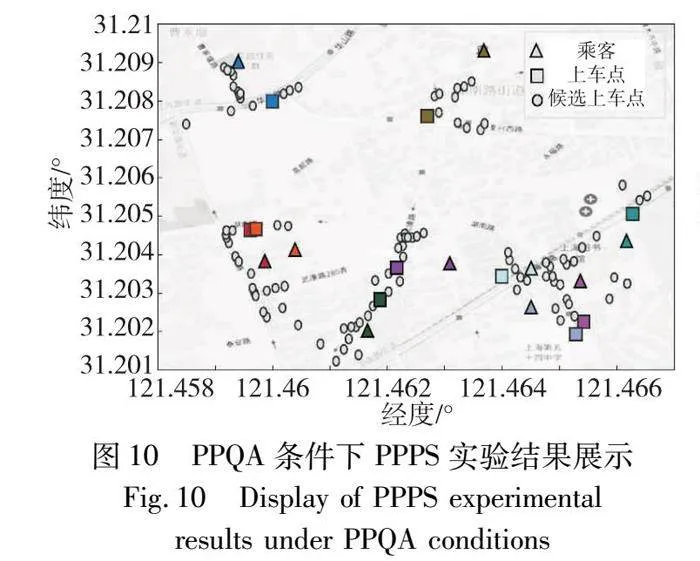
圖10中三角形圖標表示乘客，正方形圖標表示上車點，圓形圖標表示候選上車點，相同顏色表示該乘客被分配至該上車點（參見電子版）。PPPS算法將上車點作為首要考慮因素，旨在為每位乘客分配一個基于算法邏輯計算得出的最佳上車點。以深黃色乘客為例，由于步行距離最近的上車點靠近景點，基于交通情況考量，通常不被視為推薦的上車點；對于藍灰色乘客而言，盡管存在更近的上車點，但鑒于道路設計或交通規則限制，司機在此處執行車輛轉向操作存在困難，導致預估的訂單金額增加。因此，PPPS算法將該乘客分配至一個路況較好且預估訂單金額適宜的上車點，如圖10所示。

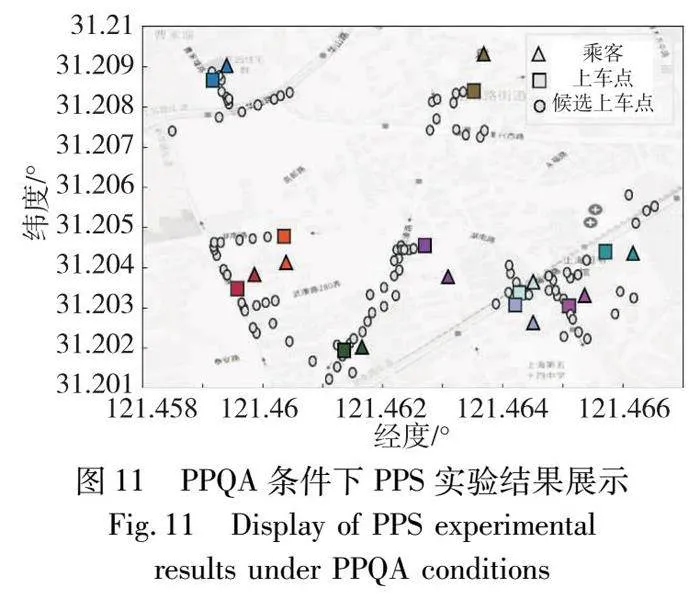
2）PPS實驗分析

圖11沿用了圖10中的表達方法展示乘客與上車點的對應關系。在該圖中，乘客與上車點的匹配結果均基于最小化乘客步行距離和步行時間的優化目標進行決策，此策略顯著凸顯了對乘客利益的優先考量，并將乘客的步行優化條件置于決策過程的核心地位。相較于其他兩種策略，乘客對該策略匹配結果的評分普遍較高，進一步驗證了該策略在提高乘客滿意度方面的有效性，如表9所示。

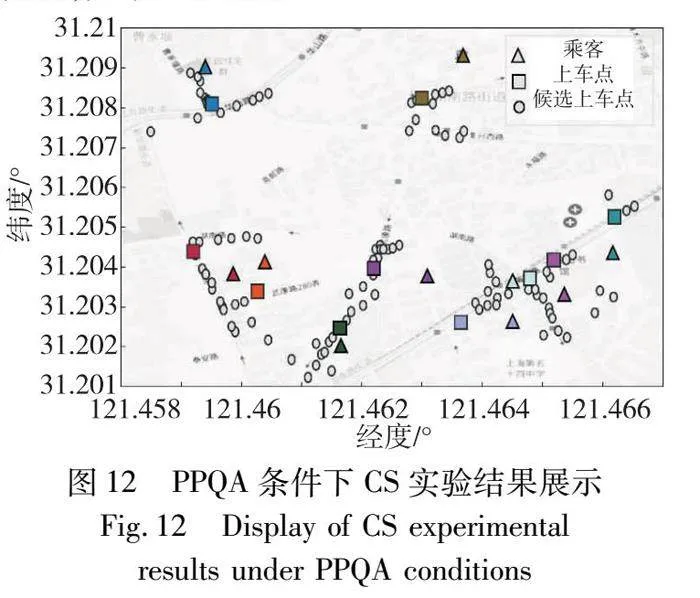
3）CS實驗分析

圖12沿用了圖10中的表達方法展示乘客與上車點的對應關系。在PPQA條件下，盡管乘客傾向于選擇最為便利的上車點，但從CS角度來看，乘客的選擇并不僅限于個人利益最大化。以上下班高峰期等特殊時間段為例，為減少交通擁堵帶來的等待時間，乘客會選擇增加步行距離，從而提高整體出行效率。然而從全局視角分析，CS策略下的平均得分指數略低于PPS［19］策略下的表現，如表9所示。

3.2.4 各影響因子真實占比分析

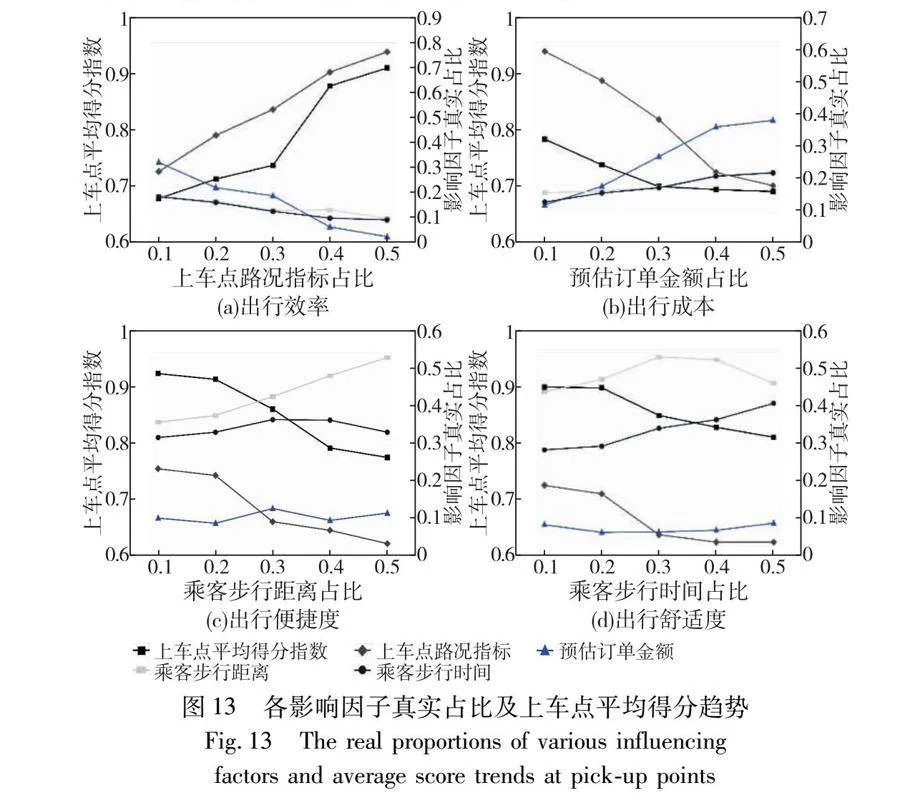
本節旨在通過調整權重參數來比較分析各影響因子真實占比之間的相關性，以及這些因素如何影響上車點平均得分指數的變化。圖13中，（a）和（b）權重參數根據PPPS［1］策略設置，（c）和（d）權重參數根據PPS［19］策略設置。

由圖13（a）可知，隨著上車點路況指標占比的增加，上車點平均得分指數呈現正相關性，且在上車點路況指標占比介于［0.3， 0.4］時，上車點平均得分增長幅度最為顯著。與此同時，預估訂單金額、乘客步行距離和步行時間真實占比均有所下降，表明當上車點路況較差時，IKM算法更加重視路況因素，以優化乘客的出行體驗。

由圖13（b）可知，預估訂單金額占比與上車點平均得分指數之間呈現出負相關性，隨著預估訂單金額占比的增加，上車點平均得分指數呈逐漸下降趨勢。此外，上車點路況指標真實占比隨著預估訂單金額占比的增加而降低，表明在高價值訂單情況下，路況因素對上車點配置的影響減弱。同時，乘客步行距離和乘客步行時間真實占比雖變化不大，但也呈現出緩慢增加的趨勢，表明在訂單金額較高時，乘客對步行距離和步行時間的敏感度有所增加，但此變化相對較小。

由圖13（c）可知，隨著乘客步行距離占比的增加，上車點平均得分指數呈現先下降后趨于穩定的趨勢，表明在乘客步行距離達到一定閾值后對上車點配置的影響減弱。同時，上車點路況指標真實占比隨著乘客步行距離占比的增加而持續下降，表明在短步行距離情況下，IKM算法更傾向于優先考慮步行距離而非上車點路況指標，以優化乘客的上車點配置。另一方面，預估訂單金額真實占比呈現緩慢增加的趨勢，表明隨著步行距離的增加，預估訂單金額在決策過程中的重要性逐漸上升。乘客步行時間真實占比隨著步行距離占比的增加而呈現出先上升后下降的趨勢，這一現象與多種因素有關，如乘客步行速度的變化、等待時間的長短、路況和環境因素等。

由圖13（d）可知，隨著乘客步行時間占比的增加，上車點平均得分指數呈現出緩慢下降后趨于穩定的趨勢，這與乘客對步行時間的敏感度有關，即在步行時間較長時，乘客更傾向于選擇得分較高的上車點以減少步行時間。同時，上車點路況指標真實占比呈現出先快速下降后趨于穩定的趨勢，反映了在步行時間較長時上車點路況指標對決策的影響減弱。預估訂單金額真實占比平緩增加且乘客步行距離真實占比先上升后下降，表明在乘客需求較低且乘客步行時間較長時，IKM算法更傾向于考慮減少乘客步行時間的上車點。

3.3 綜合分析

3.3.1 平均得分分析

由表8可知，當處于PQA條件下時，CS策略具有一定優勢，而PPPS策略的平均得分較低，與CS策略平均相差2.04%。由表9可知，當處于PPQA條件下時，PPS策略優于其他兩種方案，且PPPS 策略平均得分仍為最低，與PPS策略平均相差4.14%。

綜上所述，當處于PQA條件下時，乘車軟件應根據CS策略為乘客推薦最佳上車點；當處于PPQA條件下時，則應根據PPS策略為乘客進行推薦。在實際生活中，需根據不同的現實情況進行討論和動態推薦。

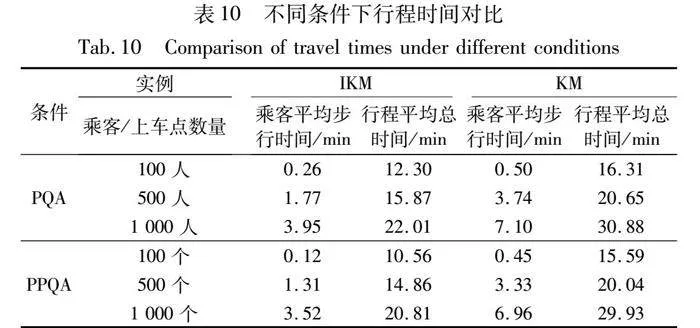
3.3.2 行程時間對比

本文設定行人步行的平均速度為60 m/min，網約車的平均行駛速度為600 m/min。表10給出了不同條件下行程時間的對比結果。

由表10可知，KM算法在處理不同規模數據時耗時明顯高于IKM算法，無法滿足乘客與上車點配置的實時性要求。由于KM算法只考慮局部最優，導致乘客平均步行時間、行程平均總時間均高于IKM算法考慮全局最優后所得出的配置結果。

4 結束語

本文提出了一種基于多模深度森林和迭代Kuhn-Munkres的動態上車點推薦算法。首先，對時空軌跡大數據進行約束處理，以提取出基于路網匹配的潛在上車點集；其次，基于乘客步行距離、步行時間、上車點路況指標以及上車點至乘客目的地的預估訂單金額等關鍵影響因子，利用多模深度森林預測算法進行最佳上車點預測；最后，通過迭代Kuhn-Munkres算法引導乘客前往最佳上車點上車，旨在減少運算資源消耗，并通過設置上車點的最大容納人數閾值來解決同一上車點多乘客導致的交通擁堵問題。實驗研究表明，本文提出的多模深度森林預測算法和迭代Kuhn-Munkres配置算法具有較高的實用性，且配置算法不僅能有效提升平均調度效果，同時在處理大規模數據集上有較高的求解效率。

本文目前僅從乘客和上車點的角度考慮上車點推薦問題，且提出的算法中的一些參數（如決策樹數量、深度、決策權重等）需事先設定，并可能對最終的預測結果和配置結果產生影響。在未來的研究中，擬考慮將司機角度納入模型范圍以進一步提升交通效率、司機接單率以及乘客滿意度；同時，將探索利用自動化參數調優技術來自動搜索最佳參數組合，以提高算法的性能和參數調節效率。

參考文獻：

［1］Zhu Wanqiu， Lu Jian， Li Yunxuan， et al. A pick-up points recommendation system for ridesourcing service ［J］. Sustainability， 2019， 11（4）： 1097.

［2］路民超， 李建波， 逄俊杰， 等. 面向出租車需求預測的多因素時空圖卷積網絡 ［J］. 計算機工程與應用， 2020， 56（24）： 266-273. （Lu Minchao， Li Jianbo， Pang Junjie， et al. Multi-factor spatio-temporal graph convolution network for taxi demand prediction ［J］. Computer Engineering and Applications， 2020， 56（24）： 266-273.）

［3］熊亭， 戚湧， 張偉斌， 等. 基于時空相關性的短時交通流預測模型 ［J］. 計算機工程與設計， 2019， 40（2）： 501-507. （Xiong Ting， Qi Yong， Zhang Weibin， et al. Short term traffic flow forecasting model based on temporal-spatial correlation ［J］. Computer Engineering and Design， 2019， 40（2）： 501-507.）

［4］陳瑞， 沈鑫， 萬得勝， 等. 面向綠色節能的智能網聯電動車調度方法 ［J］. 計算機科學， 2023， 50（12）： 285-293. （Chen Rui， Shen Xin， Wan Desheng， et al. Intelligent networked electric vehicles scheduling method for green energy saving ［J］. Computer Science， 2023， 50（12）： 285-293.）

［5］鄭渤龍， 明嶺峰， 胡琦， 等. 基于深度強化學習的網約車動態路徑規劃［J］. 計算機研究與發展， 2022， 59（2）： 329-341. （Zheng Bolong， Ming Lingfeng， Hu Qi， et al. Dynamic ride-hailing route planning based on deep reinforcement learning ［J］. Journal of Computer Research and Development， 2022， 59（2）： 329-341.）

［6］陳立軍， 張屹， 陳孝如， 等. 網約車任務分配系統優化 ［J］. 計算機系統應用， 2022， 31（6）： 19-28. （Chen Lijun， Zhang Yi， Chen Xiaoru， et al. Optimization of task allocation system for online car-hailing ［J］. Computer Systems Applications， 2022， 31（6）： 19-28.）

［7］Wang Sai， Wang Jianjun， Li Weijia， et al. Revealing the influence mechanism of urban built environment on online car-hailing travel considering orientation entropy of street network ［J］. Discrete Dynamics in Nature and Society， 2022（1）： 3888800.

［8］Agarwal S， Charoenwong B， Cheng S F， et al. The impact of ride-hail surge factors on taxi bookings ［J］. Transportation Research Part C： Emerging Technologies， 2022， 136（3）： 103508.

［9］Xia Dawen， Bai Yu， Zheng Yongling， et al. A parallel SP-DBSCAN algorithm on spark for waiting spot recommendation ［J］. Multimedia Tools and Applications， 2022，81（1）： 4015-4038.

［10］Mann S K， Chawla S. A proposed hybrid clustering algorithm using K-means and BIRCH for cluster based cab recommender system （CBCRS） ［J］. International Journal of Information Technology， 2023， 15（1）： 219-227.

［11］康軍， 張凡， 段宗濤， 等. 基于LightGBM的乘客候車路段推薦方法 ［J］. 測控技術， 2020， 39（2）： 56-62. （Kang Jun， Zhang Fan， Duan Zongtao， et al. Recommendation method of passengers’ boar-ding sections based on LightGBM ［J］. Measurement amp; Control Technology， 2020， 39（2）： 56-62.）

［12］Olakanmi O O， Odeyemi K O. A collaborative 1-to-n on-demand ride sharing scheme using locations of interest for recommending shortest routes and pick-up points ［J］. International Journal of Intelligent Transportation Systems Research， 2021， 19（6）： 285-298.

［13］Gu Shuxian， Dai Yemo， Feng Zezheng， et al. T-PickSeer： visual analysis of taxi pick-up point selection behavior ［J］. Journal of Visualization， 2024， 27（6）： 451-468.

［14］You Lan， Guan Zhengyi， Li Na， et al. A spatio-temporal schedule-based neural network for urban taxi waiting time prediction ［J］. ISPRS International Journal of Geo-Information， 2021， 10（10）： 703.

［15］Dieter P， Stumpe M， Ulmer M W， et al. Anticipatory assignment of passengers to meeting points for taxi-ridesharing ［J］. Transportation Research Part D： Transport and Environment， 2023， 121（8）： 103832.

［16］Chang Mengmeng， Chi Yuanying， Ding Zhiming， et al. A continuous taxi pickup path recommendation under the carbon neutrality context ［J］. ISPRS International Journal of Geo-Information， 2021， 10（12）： 821.

［17］Aliari S， Haghani A. Alternative pickup locations in taxi-sharing： a feasibility study ［J］. Transportation Research Record， 2023， 2677（1）： 1391-1403.

［18］Zhang Yan， Shen Guojiang， Han Xiao， et al. Spatio-temporal digraph convolutional network-based taxi pickup location recommendation ［J］. IEEE Trans on Industrial Informatics， 2023， 19（1）： 394-403.

［19］郭羽含， 劉秋月. 時空軌跡和復合收益的動態上車點推薦［J］. 計算機科學與探索， 2022， 16（7）： 1611-1622. （Guo Yuhan， Liu Qiuyue. Dynamic pickup-point recommendation based on spatiotemporal trajectory and hybrid gain evaluation ［J］. Journal of Frontiers of Computer Science and Technology， 2022， 16（7）： 1611-1622.）

［20］郭羽含， 劉雨希， 劉秋月. 動態約束與松弛分割的多目標上車點推薦 ［J］. 計算機工程與應用， 2023， 59（11）： 320-328. （Guo Yuhan， Liu Yuxi， Liu Qiuyue. Multi-objective pick-up point recommendation with dynamic constraint and relaxed segmentation ［J］. Computer Engineering and Applications， 2023， 59（11）： 320-328.）

［21］Zhang Wenbo， Ukkusuri S V. Share-a-Cab： scalable clustering taxi group ride stand from huge geolocation data ［J］. IEEE Access， 2021， 9： 9771-9776.

［22］Zhang Jing， Li Biao， Ye Xiucai， et al. Pick-up point recommendation strategy based on user incentive mechanism ［J］. PeerJ Computer Science， 2023，9（11）：e1692.

［23］Zhang Xiaojian， Zhou Zhengze， Xu Yiming， et al. Analyzing spatial heterogeneity of ridesourcing usage determinants using explainable machine learning ［J］. Journal of Transport Geography， 2024， 114（1）：103782.

［24］Nickkar A， Lee Y J， Meskar M. Developing an optimal peer-to-peer ride-matching problem algorithm with ride transfers ［J］. Transportation Research Record， 2022， 2676（11）： 124-136.

［25］Vega-Gonzalo M， Aguilera-García á， Gomez J， et al. Traditional taxi， e-hailing or ride-hailing？ A GSEM approach to exploring service adoption patterns ［J］. Transportation， 2024，51（8）： 1239-1278.

［26］Hou Yi， Garikapati V， Weigl D， et al. Factors influencing willingness to pool in ride-hailing trips ［J］. Transportation Research Record， 2020， 2674（5）： 419-429.

［27］Naumov S， Keith D. Optimizing the economic and environmental bene-fits of ride-hailing and pooling ［J］. Production and Operations Management， 2022， 32（3）： 904-929.

［28］Wang Wensi， Yu Bin， Fang Ke， et al. Causal effect of metro operation on regional resident mobility considering zone-based trip time relia-bility ［J］. Tunnelling and Underground Space Technology， 2023， 135（5）： 105041.

［29］潘志宏， 萬智萍， 謝海明. 跨平臺框架下基于移動感知的智慧公交應用研究 ［J］. 計算機工程與應用， 2018， 54（19）： 243-247， 260. （Pan Zhihong， Wan Zhiping， Xie Haiming. Research on intelligent public transport application based on mobile sensing in cross platform framework ［J］. Computer Engineering and Applications， 2018， 54（19）： 243-247， 260.）

［30］高文超， 李國良， 塔娜. 路網匹配算法綜述 ［J］. 軟件學報， 2018， 29（2）： 225-250. （Gao Wenchao， Li Guoliang， Ta Na. Survey of map matching algorithms ［J］. Journal of Software， 2018， 29（2）： 225-250.）

［31］李志超， 王艷東， 賈若霖. 基于多因子幾何匹配的AI提取路網屬性信息重建方法 ［J］. 計算機應用研究， 2021， 38（12）： 3688-3691， 3696. （Li Zhichao， Wang Yandong， Jia Ruolin. Attribute information reconstruction method of road network extracted by AI based on multi-factor geometric matching ［J］. Application Research of Computers， 2021， 38（12）： 3688-3691， 3696.）

［32］周杰英， 賀鵬飛， 邱榮發， 等. 融合隨機森林和梯度提升樹的入侵檢測研究 ［J］. 軟件學報， 2021， 32（10）： 3254-3265. （Zhou Jieying， He Pengfei， Qiu Rongfa， et al. Research on intrusion detection based on random forest and gradient boosting tree ［J］. Journal of Software， 2021， 32（10）： 3254-3265.）

［33］崔展齊， 謝瑞麟， 陳翔， 等. DeepRanger： 覆蓋制導的深度森林測試方法 ［J］. 軟件學報， 2023， 34（5）： 2251-2267. （Cui Zhanqi， Xie Ruilin， Chen Xiang， et al. DeepRanger： coverage-guided deep forest testing approach ［J］. Journal of Software， 2023， 34（5）： 2251-2267.）

［34］Liu Jiahao， Jin Hanxin， Qiang Lei， et al. Hybrid two-phase task allocation for mobile crowd sensing ［J］. Computer Engineering， 2022， 48（3）： 139-145.

［35］李曉會， 董紅斌. 基于E-CARGO模型的共乘出行匹配建模與優化方法［J］. 計算機應用， 2022， 42（3）： 778-782. （Li Xiaohui， Dong Hongbin. Modeling and optimization method of ride-sharing matching based on E-CARGO model ［J］. Journal of Computer Applications， 2022， 42（3）： 778-782.）

［36］王子慧， 任寧寧， 周毅， 等. 優化多層次分析法的影響因素績效評價模型 ［J］. 計算機工程與設計， 2023， 44（7）： 2039-2046. （Wang Zihui， Ren Ningning， Zhou Yi， et al. Optimizing perfor-mance evaluation model of influencing factors of AHP ［J］. Computer Engineering and Design， 2023， 44（7）： 2039-2046.）

［37］夏英， 石梔琦. 面向交通流量預測的多頭注意力時空卷積圖網絡模型 ［J］. 計算機應用研究， 2023， 40（3）： 766-770. （Xia Ying， Shi Zhiqi. Multi-head attention spatio-temporal convolutional graph network for traffic flow prediction ［J］. Application Research of Computers， 2023， 40（3）： 766-770.）

［38］Gallo F， Sacco N， Corman F. Network-wide public transport occupancy prediction framework with multiple line interactions ［J］. IEEE Open Journal of Intelligent Transportation Systems， 2023， 4： 815-832.

［39］Sun Dongxian， Guo Hongwei， Wang Wuhong. Vehicle trajectory prediction based on multivariate interaction modeling［J］. IEEE Access， 2023， 11： 131639-131650.