基于大模型使用方程雙重驗證提示的數學問題求解

摘 要：

盡管使用思維鏈（chain of thought，CoT）的大模型（large language model，LLM）在單未知數的數學問題求解（math word problem，MWP）任務上取得了顯著成果。但是，目前的研究缺乏適用于方程數學問題的方法。由于數學問題求解對推理步驟具有很高的敏感性，列方程出錯會導致后續步驟連環出錯，所以提出一種漸近式驗證糾正的方法2ERP，一邊驗證一邊糾正步驟錯誤，輸出最有可能的正確答案。在驗證環節使用等式和答案的雙重驗證，回代答案到等式確保計算的正確，從數學表達式獲取數值關系來驗證等式的正確性。在糾正流程中，根據回代的結果和雙重驗證的一致性排除錯誤的推理路徑，逼近正確結果。與其他CoT方法相比，2ERP方法在6個數據集上均取得了性能上的提升，平均準確率達到了66.2%，尤其是方程問題的數據集上，平均提高了6.9百分點。2ERP方法是一種設計提示的零樣本方法，通過多次迭代提高數學問題的準確率，并輸出具有詳細步驟的求解過程，該方法在方程問題上的提升更加明顯。

關鍵詞：數學問題求解；思維鏈；大語言模型；零樣本

中圖分類號：TP183"" 文獻標志碼：A""" 文章編號：1001-3695（2024）12-027-3729-06

doi： 10.19734/j.issn.1001-3695.2024.05.0153

Double validation and rectification progressive prompt for equations in math word problem based on large language model

Zhang Yinglin， Liu Changhui， Huang Shufen

（School of Computer Science amp; Engineering， Wuhan Institute of Technology， Wuhan 430205， China）

Abstract：

Although large language model using CoT method has achieved remarkable results in solving math word problem（MWP） with one unknown， there is currently a lack of methodology that is applicable to MWP involving equations. Equation problems are highly sensitive to the reasoning step， and an error in the equation-laying step can lead to a cascade of errors in subsequent steps. Therefore， this paper proposed a progressive prompt method called 2ERP， which rectified incorrect reaso-ning paths after validation and output the most likely answer. During the validation module， it substituted the answer back into the equation to ensure the accuracy of the calculation. Then， the method obtained numerical relationships from the mathematical expression to verify the equation. The rectification process approximated the correct result by eliminating incorrect reaso-ning paths based on the consistency of the double validation. 2ERP method outperformed other CoT methods， achieving an ave-rage accuracy of 66.2% on six datasets. Notably， it achieved an average improvement of 6.9% on equation problems. In conclusion， 2ERP method is a prompt-based zero-shot method， which improves the accuracy of MWP through multiple iterations and outputs a solving process with detailed steps. This method has a more significant improvement in equation problems.

Key words：math word problem; chain-of-thought（CoT）; large language model（LLM）; zero-shot

0 引言

數學是基礎教育中不可或缺的一門學科。它既是基礎學科發展的基石，也是人工智能研發的基礎。通過數學問題求解，研究者們能改進算法程序，開發出類人思考的推理模型。人類的思考方式會將復雜問題求解分解成逐個步驟，思維鏈（CoT）［1］就是采用這種直覺上的推理方法，在保證可解釋性的同時，降低一步輸出結果的難度。

數學問題求解類似做決策的過程，因此，首選自洽（self-consistency）方法［2］，它通過多次投票得到票選最多的結果。自洽采用的邊緣化采樣的解碼方式能避免每次推導出不同的答案，得到一致的推理結果。但是，該方法同樣會導致模型犯下經驗主義錯誤，一個問題采樣錯誤遺留，則一類問題均會采用遺留的錯誤路徑。再者，推理的校正過程中，要么在問題后添加之前答案的提示［H］［3］，如答案在［H］附近。要么是排除錯誤的推導結論［4］，如答案可能不是［H］。前者采用的附近提示，如果上次推導的路徑錯誤，在錯誤路徑的附近尋找仍可能導致錯誤推導。后者采用的排除提示，在方程組列錯的情況下，即使計算無誤也不一定得到正確答案。最后，數學問題的求解步驟敏感性高，步驟中的任何錯誤都可能影響到求解答案的正確性。

即使是小學階段的數學問題，也涵蓋不止一種類型的數學題目。通過對小學數學問題的分析與實驗評估，發現以下問題：a）缺乏適用于六個年級的大模型數學應用題求解方法，主要關注單未知數的問題求解；b）局限于英文數學問題，缺乏適用多語言的數學問題求解方法；c）對等式理解不足，計算能力強但求解過程容易出錯。

為了解決以上問題，本文結合方程思想，用原始的數學表達式關系表示文本關系，然后進行純粹的數學計算。既減少了推理的步驟，也專注于方程的計算求解。如下面方程數學問題的例子：

問題 青山村種的水稻產量逐年增長，2013年平均每公頃產7 200 kg，2015年平均每公頃產量比2014年多792 kg，求水稻每公頃產量的年平均增長率。

方程 7 200.0×（1.0+x）^2.0=7 200.0×（1.0+x）+792.0√

7 200.0×（1.0+x）^2.0=7 200.0×（1.0+x）×

已知設水稻每公頃產量的年平均增長率為x，等式左邊代表2015年平均每公頃產量，右邊代表2014年平均每公頃產量，再次審視發現等式并不成立，漏掉了題目中792的條件。通過方程推斷數值關系，發現等式存在錯誤，能避免重復檢查的投票流程中出現的錯誤遺留問題。

其次，未知數和方程數量增多，搜索的求解空間大小會呈指數級增長［4］。采用答案在［H］附近的提示能快速找到潛在答案，但也會局限搜索范圍降低準確度。而采用答案不是［H］的提示，在方程組和多未知數的情況下，排除效率過低。因此，結合潛在可能和排除兩種提示方法，逐步縮小求解空間大小，逼近正確求解答案。

最后，《決策與理性》［5］提到了三重心智：自主心智、算法心智和反省心智，其中反省心智輔助人類心智作出決策與判斷。大模型使用的思維鏈方法是基于直覺而非深思熟慮的，本文通過添加雙重驗證環節作為反省機制，促使大模型輸出經過考量的結果，并采用等式的驗證模塊，加強對表達式中數值的理解， 從而糾正錯誤計算結果。

對于直白的數值關系，可以按順序邏輯推理出答案。對于更復雜的問題來說，列出等式后反而將其轉換為純粹的數值計算。所以，方程求解的關鍵在于正確的數值內部關系和正確的計算結果。本文提出了一種適用于方程問題的雙重驗證漸進提示方法2ERP，這種零樣本方法既在文本理解上保證數值關系的正確，又在數值上保證計算結果的正確。本文的主要貢獻如下：

a）提出了適用于方程組求解的提示方法，并且適用于單未知數推導。

b）通過在6個數據集上進行驗證，2ERP方法在中文與英文數學問題上均適用，并且達到了66.2%的準確率。

c）通過對數學表達式和方程的數值解釋，提高了方程問題求解步驟的可解釋性，理解性更強。

1 相關工作

1.1 數學問題求解

早期，研究者們使用規則庫和統計［7，8］的方法，設計復雜的邏輯模板，并注釋文本，以識別出文本中的實體、數值和操作符號。該時期需要大量的人工標注來解決單步加減計算問題。接下來，進入到應用seq2seq和遞歸神經網絡的階段［9，10］，將問題輸入神經網絡，用樹結構［11，12］生成歸一化的算術方程，減少生成重復方程的情況，但生成的方程存在無解和無效的問題。深度學習［13～15］的方法同樣采用樹結構解碼，而且探尋了多種表達式的求解方式［16］，大幅度提高了數學問題求解的準確率。然而，優秀的數據源是深度學習方法的前提，也因此，它難以泛化到其他數學問題相關的數據集中。在前人的研究基礎上，本文的研究工作目標是生成詳細的步驟描述，通過提示大語言模型，不進行注釋和微調，求解單未知數和方程組的數學應用題。

1.2 思維鏈提示方法

思維鏈方法在自然語言的推理任務中取得了顯著成果，這些方法都根據實際應用任務有所改進。目前主流使用兩種提示方法：零樣本［17］和少樣本［18］。啟發式的零樣本方式是將問題分解，使子問題回答正確，確定分步推理的正確性。為了保證子問題的正確性，最少到最多提示（least to most）［19］從最簡單的子問題開始提問，將提問和答案合并到問題中，引導模型回答最初的提問。但是，這種方式顯露出遺漏步驟和計算錯誤的問題。因此，計劃-解決（plan-and-solve）方法［20］提出先制定解決方案，即具體的求解計劃，再根據計劃生成求解步驟，減少遺漏的問題。為了減少計算錯誤，PHP-CoT［3］和RPR-CoT［4］通過多次迭代使模型自我糾正錯誤。少樣本提示中，Manual-CoT［1］人工設計符合任務的有效提示，再提供多個例子激發模型的學習能力。Auto-CoT［21］則省去了人力成本，采用零樣本方法生成的例子，讓大模型自動構造跨任務的提示，生成合理論證。以上方法均受到人類思考方式的啟發，讓模型模仿人類處理自然語言。Program-of-Thought［22］認為編程語言是使模型理解和應用更高效的語言，所以使用編程語言和編程邏輯解釋文本。2ERP屬于零樣本方式，該方法明確步驟的重要性，在逐步驗證和糾正的過程中，核驗方程解計算過程的正確性，以保證步驟無誤，接著以方程核驗作為中間環節串聯起附近提示和排除錯誤提示，確保推導正確。

1.3 答案選擇策略

許多模型精心設計了適合構造提示的答案選擇策略，并傾向于生成一眾候選答案，再選出最佳答案。自洽方法的選擇思路是，最佳答案通過多數投票取勝，獲得任務性能的提升。另一種思路是將候選答案全部評分，取最高分為最佳答案。Cobbe等人［23］訓練獨立的生成器與驗證器，兩套系統合作監督推理步驟與路徑選擇，根據評分高低挑選最合適的路徑和答案。Shen等人［24］則是將結果排名作為影響因素，聯合訓練生成器和排名器，選擇了排名第一的生成方案作為答案。Cobbe等人［25］同樣選擇用最高分的挑選方式，但使用大模型本身作為評估者。2ERP方法選擇了與文獻［3，4］一致的路線，不會對每個問題都生成一系列候選答案，而是一邊生成推理路徑，一邊驗證并糾正，并且無須特別設計的選擇策略，減少特定任務的工作量。

2 方法

2.1 大模型基座

ChatGLM3［28］是智譜AI和清華大學 KEG 實驗室聯合發布的開源對話預訓練模型。ChatGLM3-6B是10 B以下的基礎模型中取得執行通用任務優異結果的大模型，所以本文選擇ChatGLM3作為大模型訓練的基座。在大模型中，提示工程達到了與經過微調的大模型同樣甚至更強的推理水準［3，4］。為了使方法適用于求解六個年級的小學數學問題，并生成詳細的求解步驟，本文設計了漸進式的提示指令，使大模型在迭代的過程中自我糾正錯誤，提升數學問題求解的準確度。

2.2 提示設計

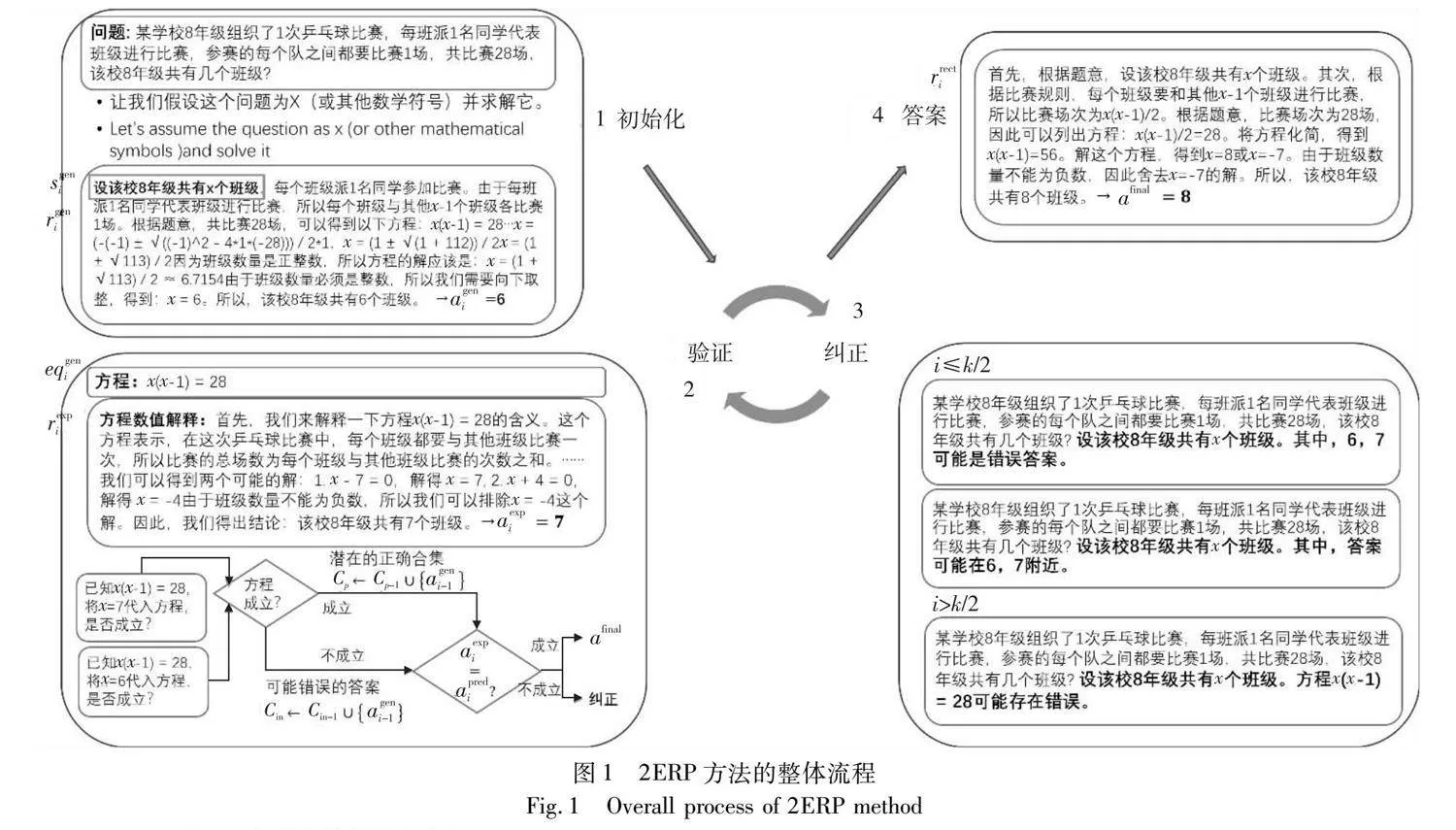
2ERP方法提出的雙重驗證的漸進式提示包含三個模塊的算法步驟，具體如圖1所示。2ERP的首要步驟是初始化，已知問題Q，輸入大模型后得到初始化推理過程rgen0，從推理過程中得到答案agen0，并將可能錯誤合集Cin和潛在正確合集Cp設為空集。其中，初始化的答案是agen0=6。接著進入驗證流程，根據初始化推理過程rgen0中取得未知數的假設sgen0。首先，從初始化路徑取得方程eqgen0：x（x-1）=28，并提示大模型對方程進行數值解釋rexp0，得到數值解釋的答案aexp0=7。正式開始驗證，先驗證答案agen0和 aexp0是否求解正確，再看兩者是否相等，只有兩種驗證均正確時，才會結束流程。顯然兩者并不相等，所以繼續進入糾正環節。

驗證過程中，可能錯誤合集Cin和潛在正確合集Cp也會隨著ageni和 aexpi的比較情況更新對應合集。圖1中的驗證環節比較滿足第1輪次和驗證不成立的條件，更新可能錯誤合集Cin={［6，7］}，并選擇排除的提示模板，生成糾正后推理路徑rrect1并獲取答案agen1=8。再次進入驗證流程發現滿足驗證條件，將生成的推理路徑答案作為最終答案，因為當前問題只存在一個求解答案，所以afinal=8。整個驗證糾正提示流程涉及的詳細符號定義如表1所示。

2.2.1 初始化

初始化步驟使用圖1中提示，該提示適用于方程求解，如果使用Kojima等人［17］的初始化方法，難以得到方程解釋rexpi。數值答案的獲取部分rexpi的準備工作，需要先從推理路徑rgeni獲得假設sgeni。除了推理路徑外，將不正確數值合集Cin和潛在數值合集Cp也設為，為驗證步驟做準備。

2.2.2 驗證模塊

驗證模塊需要上一步生成的推理路徑rgeni作為條件，按照模板所示的“Q： rgeni中的方程或方程組（不包含推斷和描述語句）為：”，獲取方程eqgeni。接下來，通過構造的提示“［Q］， 方程［Eq］的數值解釋是什么？”生成對方程數值理解的推理步驟rexpi，并對rexpi提問截取的問題語句q得到答案 aexpi，其中［Q］表示問題文本，q表示文本中的提問。驗證第一步，回代答案到方程中，驗證答案是否正確求解。按照設計的一個簡單模板“Q：將［A］代入［Eq］，答案［A］是否使方程或方程組成立？”，讓大模型驗證答案能否使等式成立。其中，［A］表示待填充的答案槽，［Eq］表示待填充的方程槽。答案求解錯誤，則添加到排除答案合集Cin中，驗證正確，則添加到潛在答案合集Cp中。

第二步，判斷從文本轉換為方程求解的答案ageni是否等于從方程理解文本并求解的答案aexpi。直接比較數值得到判斷結論。

自此，兩步驗證完畢，只有同時滿足ageni和aexpi回代成立，且ageni=aexpi時，說明所列方程正確，答案計算正確，迭代結束，否則進入糾正環節。

2.2.3 糾正模塊

糾正方式的選擇依賴于驗證模塊的狀態。用潛在的答案合集和可能的錯誤合集，逼近答案的求解范圍，糾正的三種方式如下。如果計算答案回代后等式成立，但兩種答案不相同，則進入計算錯誤的糾正流程。將潛在合集Cp={aver0，…，averi－1}作為［A］的依據，按照以下模板“Q： ［Q］，其中，答案可能在［A］附近。”再者，如果答案回代后正確與錯誤結果均存在，則將錯誤合集Cin={aver0，…，averi－1}作為［A］的依據，構造排除提示：“Q： ［Q］， 其中，［A］可能存在錯誤。”最后，如果答案回代結果均錯誤，且錯誤答案不同，則進入所列方程錯誤的糾正流程，組建類似排除答案提示“Q： ［Q］，［Eq］可能存在錯誤。”輸出糾正的推理路徑rrecti。

在迭代過程中，如不滿足驗證條件，則根據情況選擇前兩種提示之一，直到第k/2輪次時，仍不滿足條件，采用最后一種模板提示，糾正錯誤方程，最后得到答案afinalj。

3 實驗與分析

3.1 數據集

數據集包含中文和英文兩類，兩種語言均包含單方程數據和方程組數據集。詳細的數據集介紹如表2所示，其中的平均單詞長度，是根據所有問題的長度（已經去除標點符號和空白字符）除以問題個數得出的結果，作為分析數學問題文本難度的參考。不相關的數值內容比例表示與計算不相關的數值內容，如問題文本中存在的年份、年級等背景數值，提供文本信息但不納入計算，該指標的計算方式是匹配的不相關數值在所有數值中的比例。

a）HMWP［16］，涵蓋大多數小學數學應用題情況的中文數據集，包括表格轉述文字的問題，文言文描述的文本，且存在阿拉伯數字與簡寫漢字替換的干擾。

b）Math23K［10］，大型中文數據集，包含四種運算的小學數學問題，且問題需要多步推導才能求解。

c）CM17K［6］，面向6～12年級，包含四種數學問題類型的中文數據集，樣本數超過17 000，涵蓋關于MWP的大多數情況，足以驗證數學單詞問題解決程序的通用性。

d）Draw［26］，包含方程組的小型英語數據集，總共有三種類型的數學問題。

e）GSM8K［25］，英文數據集，具有詳細推導步驟的單未知數數據集，來源于小學數學的高質量數據集。

f）SVAMP［27］，英文數據集，題目來源于小學四年級數學題，包含1 000個經過設計的單未知數問題，存在無關信息、實體替換等干擾，適合測試方法的穩定性。

3.2 基線

分別選擇零樣本和少樣本的方法作為基線。零樣本選擇四種方法：Direct直接向大模型輸入問題；Zero-Shot-CoT在問題后添加提示“Let’s think step by step”［1］；Plan-and-Solve先制定出計劃再解決問題，添加“Let’s first understand the problem and devise a plan to solve the problem. Then let’s carry out the plan and solve the problem step by step”［20］提示；RPR-CoT是逐步的驗證糾正流程。在驗證時掩蓋問題中的數字X，將已求出的答案作為已知條件，求解遮蔽的數字X。如果求解的數字X與原數字X不一致則進入糾正環節，糾正時根據提示排除可能的錯誤答案。

少樣本選擇三種方法：Manual-CoT提供8個有詳細求解步驟的問題作為樣本，使模型學習求解方式；Auto-CoT通過Sentence-BERT［29］模型得到聚類結果，挑選聚類的各類別問題作為樣本供模型學習；PHP-CoT提示上一步的答案生成推理路徑，直至生成結果一致。

3.3 答案評估

對比實驗的七種方法均按照論文中描述的方法實現，最終的答案以準確率為評估標準。 由于agoldj有分數或循環小數形式的答案存在，而大模型的計算精度不高，所以按以下標準判斷，agoldj和afinalj的誤差小于10－5時，答案正確，否則afinalj錯誤。同時，答案個數應與問題個數匹配，單個問題的答案L=1，多個問題則權重根據L均分。具體公式如下，其中，Q表示問題個數，L表示實際答案個數。

acc=1|Q|1|L|∑q∈Q ∑j∈L1（afinalj，agoldj）（1）

1（afinalj，agoldj）=1" |afinalj－agoldj|lt;1×10－5

0" |afinalj－agoldj|≥1×10－5 （2）

3.4 實驗結果分析

3.4.1 實驗方法對比

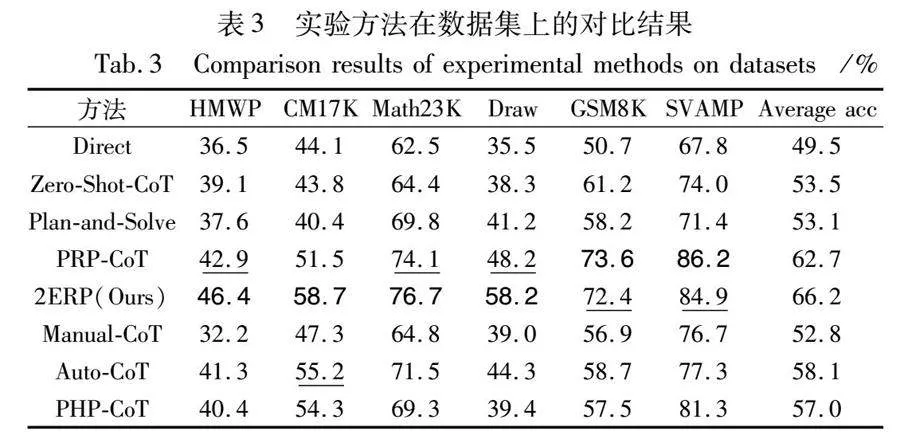
使用開源的ChatGLM3-6B模型生成推理路徑。對比實驗的結果如表3所示，2ERP與七種方法相比取得了不同程度的提升。2ERP方法在四個數據集上取得了最先進的結果，其中在三個有方程的數據集HMWP、CM17K和Draw上相較于PRP-CoT方法平均提高了6.9百分點，在另外兩個數據集GSM8K 和 SVAMP上的結果比少樣本方法平均高出8.6百分點。四個數據集中主要的提升數據集是 HMWP 和 Draw，兩者都是方程數據集。作為一種零樣本方法，在六個數據集上均達到比少樣本優異的結果。與在單未知數問題上表現出色的零樣本方法 PRP-CoT 相比，2ERP方法在方程數據集上的提升更大。

2ERP方法在四個數據集上提升明顯。與以往最先進的PRP-CoT方法相比，在Math23K數據集提升了2.6百分點是因為其數據集提問方式簡單直接。數據集Draw，CM17K和HMWP都包含線性問題和方程問題，剩下的GSM8K和SVAMP數據集的提升差距與數據集的難度相關。如表2所示，兩者均有部分不相關數值的比例，其中SVAMP數據集的干擾信息會影響大模型對數字與其相關信息的判斷。由于PRP-CoT采用遮蔽隨機數值再驗證的方式，所以PRP-CoT方法在英文單方程數據集上準確率高。PRP-CoT方法在Draw數據集上提升效果不如2ERP方法，因為Draw數據集的不相關數值比例比SVAMP更高，但其不相關的數字實際是文本的背景信息如年份、年級等，過多背景數值信息導致PRP-CoT難以在有限輪次內遮蔽實際有意義的數值進行驗證，所以其在中文數據集上適用性不強。然而采用方程驗證提示的2ERP方法不會受到相關數值的限制，所以在Draw數據集上使用RP方法提升的準確率比在SVAMP數據集上使用少樣本方法的準確率高6.4百分點。在單方程數據集上，PRP-CoT方法仍具有優勢。

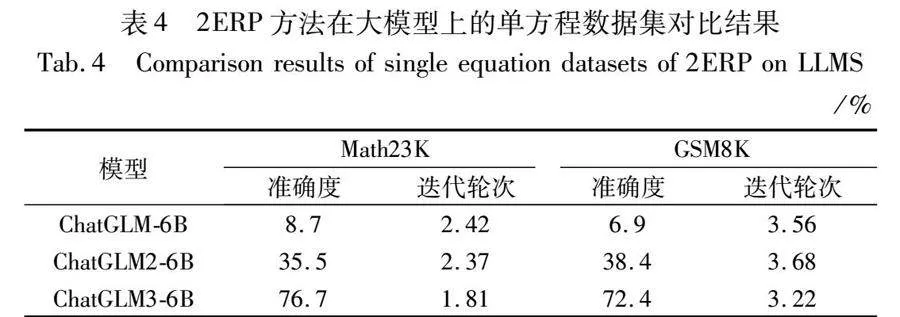
3.4.2 大模型對比分析

使用不同的大模型，在Math23K和GSM8K的單方程數據集上進行對比實驗。表4呈現出平均的準確度和迭代次數，其中，平均迭代輪次的計算是將各個迭代輪次與對應迭代次數的問題數相乘求和，再取得平均值作為結果。隨著大模型的迭代，準確率在逐步提升，平均迭代次數整體上逐漸減少。ChatGLM是基于自回歸 （generative language model， GLM）架構的大模型，特點在于二維位置編碼和亂序的空白位置預測設置，但執行數學推理任務的效果不太好。經過改進的ChatGLM2模型，整體架構對標LLaMA架構，從原來對每個GLMBlock做二維位置編碼變成了做旋轉式位置編碼（rotary position embedding， RoPE），高效率地捕捉序列元素的相對位置信息，所以在兩個單方程數據集上，ChatGLM2模型的準確度均平均提升33%，生成推理路徑效率提升，平均迭代次數減少。ChatGLM3模型的架構與二代基本一致，RoPE對象由每個GLMBlock變為全局。相較于ChatGLM2模型，ChatGLM3在Math23K和GSM8K數據集上平均提高了37.6百分點，推理性能的提升使得平均迭代次數下降。

3.4.3 數值關系驗證結果

2ERP方法設計的方程驗證流程，使模型學會了從方程中得到數值關系，并與文本中抽取的數值關系進行核驗，確保列方程步驟正確，再考慮答案計算是否準確。如表5所示，驗證過程讓模型重新思考數值與未知數對應的含義，單未知數的數據集顯示出文字解釋的數學表達式，使求解步驟的理解性更強，如23+y=Initial number of children on the bus。如表6所示，方程組問題則詳細解釋等式的推導過程，并呈現具體的計算過程。

4 消融實驗

4.1 輪次選擇

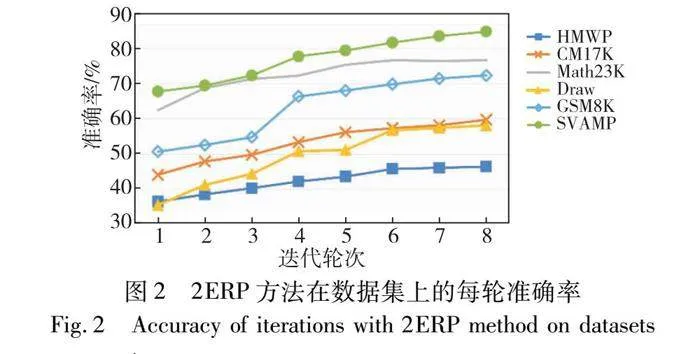
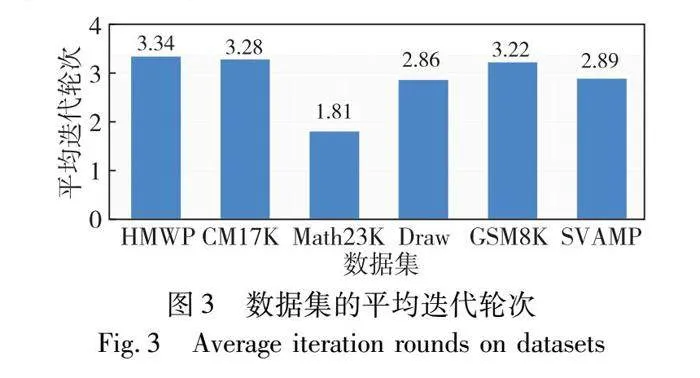
為了保證數學求解任務的準確率和推理速度，手動設置退出輪次是必要的。如圖2所示，隨著整個流程的驗證校正次數增多，準確率也逐步提高，k＝6時，大部分數據集的準確率趨于穩定。圖3使用2ERP方法在六個數據集上實驗的平均迭代輪次在3輪左右，其中Math23K的迭代輪次接近2，理想輪次的設置應為k=4。但隨著輪次增加，準確率仍有提高，尤其是平均輪次最高的Draw和CM17K。最后，綜合對平均輪次和準確率的考量，2ERP方法選擇k=6，使模型能高效且準確地完成推理。

4.2 逼近的解空間

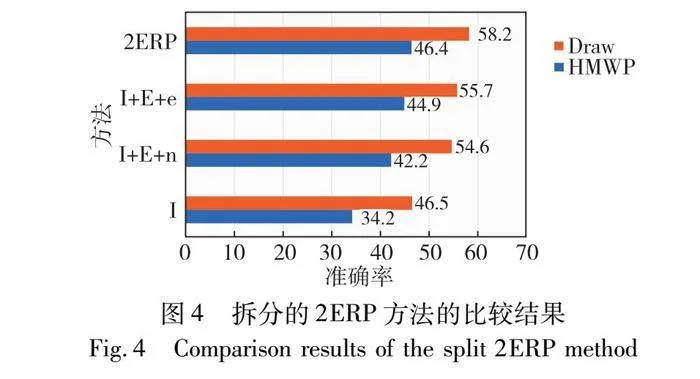
如圖4所示，I、 E、n和e表示以下內容：I表示初始化；E表示方程驗證模塊；n表示附近提示；e表示排除提示，具體提示模板已在第2章闡述。I+E+n和I+E+e分別使用了提示可能解和排除錯誤解的方法，與只用初始化方法l比較，在HMWP和Draw數據集上平均提高了8.05和9.95百分點，其中排除解的方法I+E+e提升幅度更大。本文用方程組驗證作為中間部件連接兩種方法，縮小方程組的解范圍。在HMWP和Draw數據集上，2ERP方法比初始化方法在HMWP和Draw數據集上分別提高了12.2和11.7百分點。

4.3 等式驗證的有效性

對于大模型推導任務來說，步驟的正確性，會影響到結果的準確性。復雜的問題不止考驗解題思路，同樣考驗計算能力。因此，計算步驟正確是解題正確的充分條件，尤其是容易出錯的方程求解過程。如圖4所示，在HMWP和Draw數據集上，添加雙重驗證的方法比對應的漸近方法的準確率平均提高了2.85和3.05百分點。

5 結束語

本文提出了2ERP的零樣本方法，它適用于多未知數和單未知數的數學問題求解任務。2ERP通過等式的雙重驗證，在漸近的驗證糾正過程中，逐步逼近方程的求解空間。并在推理路徑中，實現了對等式或表達式的數值解釋，理解性更強。2ERP方法在包含中文和英文的六個數據集上的平均準確率為66.2%，并與之前最好的研究方法相比，將方程數據集HMWP、CM17K和Draw的平均準確率提高了6.9百分點。

方程數據集的思維鏈推導過程仍然具有很大的上升空間，尤其是在理解圖形、計算體積等需要前置知識的問題上，思維鏈效果提升不明顯。因此，下一步研究準備通過注入常識知識提升需要數學基礎的題型的準確率。再者，如何將思維鏈方法運用在1 B參數的模型上也是一種挑戰。

參考文獻：

［1］Wei J， Wang Xuezhi， Schuurmans D， et al. Chain-of-thought prompting elicits reasoning in large language models ［J］. Advances in Neural Information Processing Systems， 2022， 35： 24824-24837.

［2］Wang Xuezhi， Wei J， Schuurmans D， et al. Self-consistency improves chain of thought reasoning in language models ［EB/OL］. （2022-05-21） ［2024-05-06］. https：//doi. org/10. 48550/arXiv. 2203. 11171.

［3］Zheng Chuanyang， Liu Zhengying， Xie E， et al. Progressive-hint prompting improves reasoning in large language models ［EB/OL］. （2023-08-10） ［2024-05-06］. https：//doi. org/10. 48550/arXiv. 2304. 09797.

［4］Wu Zhenyu， Jiang Meng， Shen Chao. Get an A in math： progressive rectification prompting ［C］// Proc of AAAI Conference on Artificial Intelligence. Palo Alto， CA： AAAI Press， 2024： 19288-19296.

［5］Stanovich K. Rationality and the reflective mind ［M］. Oxford：Oxford University Press， 2011.

［6］Qin Jinghui， Liang Xiaodong， Hong Yining， et al. Neural-symbolic solver for math word problems with auxiliary tasks ［EB/OL］. （2021-07-03）［2024-05-06］. https：//arxiv.org/abs/2107.01431.

［7］Zhang Dongxiang， Wang Lei， Zhang Luming， et al. The gap of semantic parsing： a survey on automatic math word problem solvers ［J］. IEEE Trans on Pattern Analysis and Machine Intelligence， 2019， 42（9）： 2287-2305.

［8］Zhou Lipu， Dai Shuaixiang， Chen Liwei. Learn to solve algebra word problems using quadratic programming ［C］// Proc of Conference on Empirical Methods in Natural Language Processing. New York： ACM Press， 2015： 817-822.

［9］Wang Lei， Zhang Dongxiang， Zhang Jipeng， et al. Template-based math word problem solvers with recursive neural networks ［C］// Proc of AAAI Conference on Artificial Intelligence. Palo Alto，CA： AAAI Press， 2019： 7144-7151.

［10］Wang Yan， Liu Xiaojiang， Shi Shuming. Deep neural solver for math word problems ［C］// Proc of Conference on Empirical Methods in Natural Language Processing. Palo Alto， CA： AAAI Press， 2017： 845-854.

［11］Wang Lei， Wang Yan， Cai Deng， et al. Translating a math word problem to a expression tree ［C］// Proc of Conference on Empirical Methods in Natural Language Processing. New York： ACL Press， 2018： 1064-1069.

［12］Xie Zhipeng， Sun Shichao. A goal-driven tree-structured neural model for math word problems ［C］//Proc of the 28th International Joint Conference on Artificial Intelligence. San Francisco： Morgan Kaufmann， 2019： 5299-5305.

［13］Liang Zhenwen，Zhang Jipeng，Wang Lei，et al. MWP-BERT： numeracy-augmented pre-training for math word problem solving ［EB/OL］. （2021-07-28）［2024-05-06］. https：//arxiv.org/abs/2107.13435.

［14］Zhang Jipeng， Lee R K W， Lim E P， et al. Teacher-student networks with multiple decoders for solving math word problem ［C］// Proc of the 29th International Conference on International Joint Conferences on Artificial Intelligence. San Francisco： Morgan Kaufmann， 2021： 4011-4017.

［15］Zhang Wenqi， Shen Yongliang， Ma Yanna， et al. Multi-view reaso-ning： consistent contrastive learning for math word problem ［C］// Proc of Conference on Empirical Methods in Natural Language Processing. New York： ACL Press， 2022： 1103-1116.

［16］Qin Jinghui， Lin Lihui， Liang Xiaodan， et al. Semantically-aligned universal tree-structured solver for math word problems ［C］// Proc of Conference on Empirical Methods in Natural Language Processing. New York： ACL Press，" 2020： 3780-3789.

［17］Kojima T， Gu S S， Reid M， et al. Large language models are zero-shot reasoners ［J］. Advances in Neural Information Processing Systems， 2022， 35： 22199-22213.

［18］Brown T， Mann B， Ryder N， et al. Language models are few-shot learners ［J］. Advances in Neural Information Processing Systems， 2020， 33： 1877-1901.

［19］Zhou D， Schrli N， Hou Le， et al. Least-to-most prompting enables complex reasoning in large language models ［EB/OL］. （2022-05-21） ［2024-05-06］. https：//doi. org/10. 48550/arXiv. 2205. 10625.

［20］Wang Lei， Xu Wanyu， Lan Yihuai， et al. Plan-and-solve prompting： improving zero-shot chain-of-thought reasoning by large language mo-dels ［C］// Proc of the 61st Annual Meeting of the Association for Computational Linguistics. New York： ACL Press， 2023： 2609-2634.

［21］Zhang Zhuosheng， Zhang A， Li Mu， et al. Automatic chain of thought prompting in large language models ［EB/OL］. （2022-10-07）［2024-05-06］. https：//doi. org/10. 48550/arXiv. 2210. 03493.

［22］Chen Wenhu， Ma Xueguang， Wang Xinyi， et al. Program of thoughts prompting： disentangling computation from reasoning for numerical reasoning tasks ［EB/OL］. （2023-10-23） ［2024-05-06］. https：//doi. org/10. 48550/arXiv. 2211. 12588.

［23］Zhu Xinyu， Wang Junjie， Zhang Lin， et al. Solving math word problems via cooperative reasoning induced language models ［C］// Proc of the 61st Annual Meeting of the Association for Computational Linguistics. New York： ACL Press， 2023： 4471-4485.

［24］Shen Jianhao， Yin Yichun， Li Lin， et al. Generate amp; Rank： a multi-task framework for math word problems ［C］// Proc of Conference on Empirical Methods in Natural Language Processing. New York： ACL Press， 2021： 2269-2279.

［25］Cobbe K， Kosaraju V， Bavarian M， et al. Training verifiers to solve math word problems ［EB/OL］. （2021-10-27） ［2024-05-06］. https：//doi. org/10. 48550/arXiv. 2110. 14168.

［26］Upadhyay S， Chang M W. Annotating derivations： a new evaluation strategy and dataset for algebra word problems ［C］// Proc of the 15th Conference of the European Chapter of the Association for Computational Linguistics. 2017： 494-504.

［27］Patel A， Bhattamishra S， Goyal N. Are NLP models really able to solve simple math word problems？ ［C］// Proc of Conference of the North American Chapter of the Association for Computational Linguistics： Human Language Technologies. 2021： 2080-2094.

［28］Zeng Aohan， Liu Xiao， Du Zhengxiao， et al. GLM-130B： An open bilingual pre-trained model ［EB/OL］. （2023-10-25） ［2024-05-06］. https：//doi. org/10. 48550/arXiv. 2210. 02414.

［29］Reimers N， Gurevych I. Sentence-BERT： sentence embeddings using siamese BERT-networks ［C］// Proc of Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing. 2019： 3982-3992.