高速公路改擴建施工區通行能力計算模型研究

作者簡介：

彭 旭（1991—），工程師，主要從事高速公路建設項目現場工程管理工作。

摘要：文章分析高速公路雙向四車道兩側拼寬成雙向八車道施工控制區各區段的交通特征，發現上游過渡區是施工控制區的瓶頸。根據實測數據，分別建立了基于速度-流量模型和基于影響因素修正模型的通行能力計算方法。研究結果證明這兩種方法均可用來計算施工區通行能力值，且與實測數據的相對差值在5%以內，應用這兩種方法確定了柳南高速公路改擴建項目半幅封閉施工區上游正常區、上游警告區、上游過渡區、施工作業區的通行能力推薦值分別為：1 712 pcu·h-1·ln-1、1 590 pcu·h-1·ln-1、1 331 pcu·h-1·ln-1、1 361 pcu·h-1·ln-1。

關鍵詞：交通工程；通行能力；速度-流量模型；影響因素修正模型；施工控制區；交通特征

中圖分類號：U412.36+6文獻標識碼：A 21 066 5

0 引言

隨著我國經濟的持續快速發展，現有高速公路交通量年均增長＞10%，甚至＞20%，已遠超高速公路規劃期間的預測交通量，高速公路改擴建成為未來高速公路建設的重點發展方向［1］。高速公路施工區環境復雜，交通情況跟正常運營時間段差異大，采用合理、有效的方法確定施工區的實際通行能力，有助于交通組織設計規劃，促進公路的安全運營。

Benekohal等提出了基于速度—流量曲線和修正模型的施工區運行速度和通行能力的計算方法［2］。唐智等分析并比較了以設計速度為標準和以自由流速度為標準的通行能力計算方法，發現后者更科學、更合理［3］。Yeom等整理美國高速公路工作區通行能力的數據，提出了考慮車道關閉情況、白天或夜間工作條件等影響因素的修正模型［4］。魏雪延等通過VISSIM仿真軟件和控制單一變量法對模型參數進行標定［5］，總結出多車道高速公路通行能力計算模型。劉偉銘，梁雪根據實際事故道路的交通條件，確定了考慮阻塞車道數、阻塞長度和大車型比例因素的通行能力計算模型［6］。Jehn等通過仿真建立高速公路施工區通行能力隨機估計模型，該模型能夠對不同道路幾何條件、交通條件下的通行能力進行估計，具有很好的適用性［7］。Bian等根據施工區車道開放情況、大型車比例、施工強度和施工持續時間建立神經網絡模型，預測施工區在不同的道路交通情況、運營條件下的通行能力［8］。薛行健等建立了快速路匝道主線和匝道流量、加速車道長度與通行能力三者之間的數量關系模型，發現當主線外側車道流量在1 300 pcu·h-1～1 500 pcu·h-1時最易形成通行瓶頸［9］。孟祥海等利用Greenshields模型確定各主要區段的道路通行能力，發現施工作業區段的道路通行能力只有正常路段的89%左右［10］。邵長橋等采用實測數據和仿真分析相結合的方法，分析了施工區不同控制段、不同車道間交通流的相互影響，將施工區通行能力定義為排隊通過流率［11］。宋婉璐等通過對超窄雙車道公路進行實地調查與相應的仿真測算，提出了“會車率”概念，將會車率曲線臨界點的通行能力值1 700 pcu·h-1作為窄雙車道的通行能力［12］。

本文結合實測數據，分析并歸納了雙向四車道高速公路兩側拼寬成雙向八車道半幅封閉施工作業時道路各區段的交通特征，確定了施工作業控制區的瓶頸段，使用基于速度-流量模型和基于影響因素修正模型的兩種施工區通行能力計算模型，計算了施工作業區主要區段的通行能力值，為施工區施工建設、交通組織提供理論支持。

1 施工調查與交通流數據采集

本文數據采集于某柳南高速公路改擴建項目，改擴建采取半幅封閉施工的方式沿現有雙向四車道高速公路兩側拼寬成雙向八車道。

交通流特征數據主要通過無人機拍攝車流視頻并輔以攝像機以及雷達和磁感應裝置進行采集，統計施工區域內的車輛信息、交通量、行車速度等參數。在組織和分析時，以5 min為統計間隔，并將數據乘以12，以此得到標準車輛的小時交通流量和區間平均速度。

2 高速公路改擴建保通車施工時施工控制區的交通特征分析

半幅封閉施工是常用的高速公路改擴建方式之一。在施工作業控制區段，高速公路半幅封閉，交通流從中央分隔帶的開口處轉移到另外半幅路段通行，施工區路面施工完畢后，開放雙向四車道，對另外半幅采用同樣的方式進行施工。

高速公路半幅施工時，道路交通控制段劃分為施工警告區（S）、上游過渡區（LS）、上游緩沖區（H）、施工作業區（G）、下游過渡區（LX）以及施工終止區（Z），見圖1。

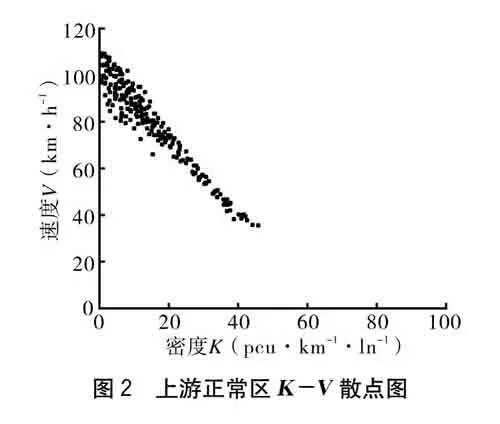
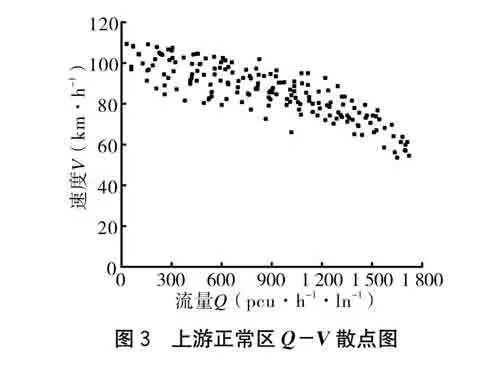
為了對比高速公路改擴建施工區交通流與正常區段交通流的區別，在施工作業控制區上游2 km處采集正常區段的交通流信息。從圖2、圖3可以得出，在遠離施工控制區的正常區段，流量＜1 600 pcu·h-1·ln-1、密度＜25 pcu·km-1·ln-1時，交通處于非擁擠狀態且行車速度基本都＞60 km·h-1，通過的最大流量為1 750 pcu·h-1·ln-1。

車流在經過施工作業區后，逐漸駛回原車道，與施工作業區相比，下游過渡區和施工終止區的通行能力得到進一步提高，位于正常區和施工區之間，不是瓶頸路段，可不對其進行分析。

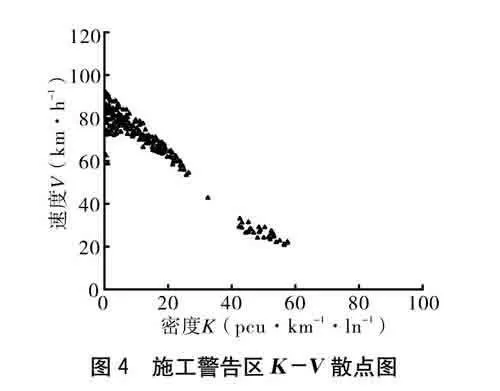
（1）施工警告區（S），是施工作業控制區的起點，設置有限速標志、施工預告標志等，提醒車輛駕駛員已進入施工區域，區段長度設置為1 600 m，限速80 km·h-1。從圖4、圖5可以得出，當流量到達1 450 pcu·h-1·ln-1、密度＞35 pcu·km-1·ln-1時，車流會進入擁擠狀態，能通過的最大流量為1 590 pcu·h-1·ln-1。

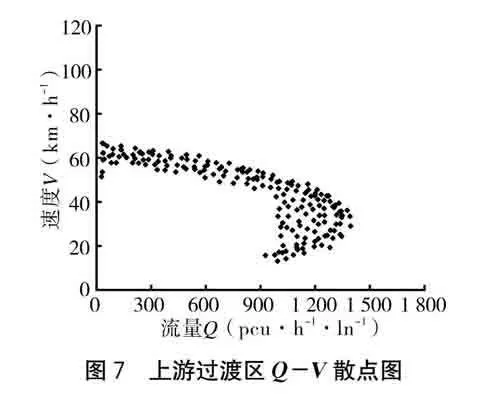
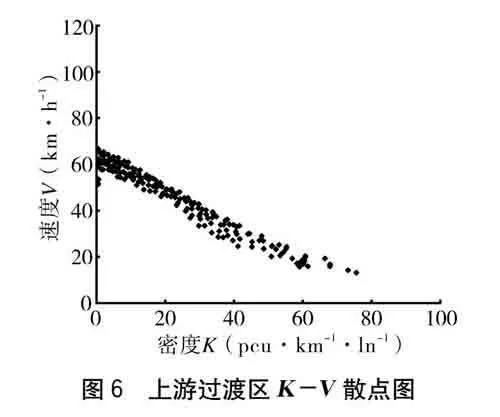
（2）上游過渡區（LS），是交通流運行狀態發生改變的初始控制段，在過渡區設置導向標志牌引導車流變道，長度設置為120 m，限速60 km·h-1。從圖6、圖7可以得出，最大流量為1 328 pcu·h-1·ln-1，在流量到達1 000 pcu·h-1·ln-1、密度＞23 pcu·km-1·ln-1時，車流就會進入擁擠狀態，并且交通流會出現紊亂，這是因為上游過渡區存在大量的換道行為。

（3）上游緩沖區（H），連接上游過區段和施工作業區，設置交通錐、隔離墩等對行車道與施工區進行隔離，長度設置為100 m，限速60 km·h-1，讓駕駛員適應工作區行駛環境的同時，保護施工人員開展施工作業。

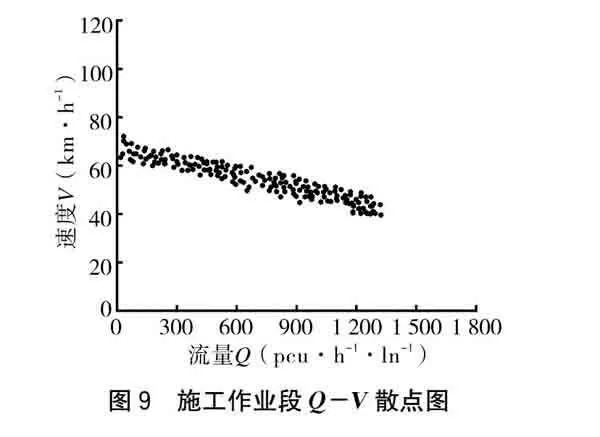
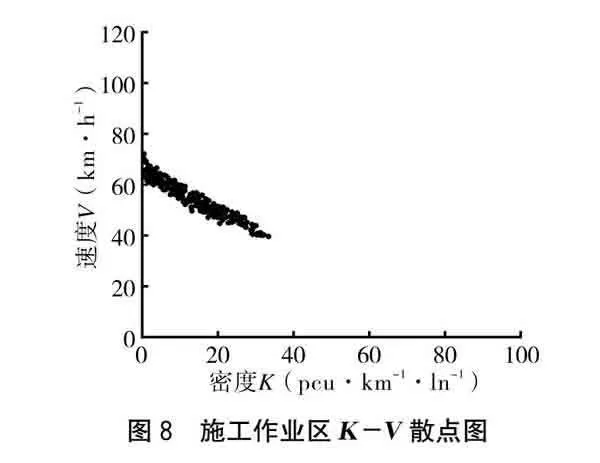
（4）施工作業區（G），是高速公路改擴建的施工區域，車道與施工作業區中間設置隔離帶，長期施工時長度≥4 km，限速60 km·h-1。從圖8、圖9可以看出，當流量＜135 pcu·h-1·ln-1、密度＜35 pcu·km-1·ln-1時，車流處于非擁擠狀態，車速基本保持在＞40 km·h-1。

（5）下游過渡區（LX）。施工作業區通過布置錐形交通標志設置后漸變區，使車輛經過時，可以按照指示行駛回原來正常車道上來，長度設置為40 m，限速60 km·h-1。

（6）終止區（Z）。標志著作業區結束的區段，車輛可以駕駛到原來正常的車道。為了行車的連續性，設置長度為40 m，末端設置解除限速標志。

分析各施工區段交通流特征可以發現，上游警告區、上游過渡區的最大流量分別為正常路段的90%、76%。上游正常區和上游警告區在車流密度到達35 pcu·km-1·ln-1時進入擁擠狀態，而上游過渡區在密度到達23 pcu·km-1·ln-1時進入擁擠狀態。由此可見，施工對交通有顯著的影響，上游過渡區因為存在大量的換道行為導致其成為施工控制區交通的瓶頸路段，是交通流受施工影響最嚴重的區段。

3 基于速度-流量模型的通行能力計算方法

根據實際采集的交通流數據，結合施工區交通流特征和以往學者研究，流量、速度和密度間具有緊密聯系，為此采用格林希爾治模拋物線模型建立速度-流量模型以計算通行能力，見式（1）。

Q=kj（V-V2Vf）

（1）

式中：Q——車流量；

V——區間平均速度；

K——車流密度；

Vf——暢行速度，取道路通暢，車輛無阻時的平均速度；

Kj——為阻塞密度，取道路阻塞，車輛停止移動時的密度。

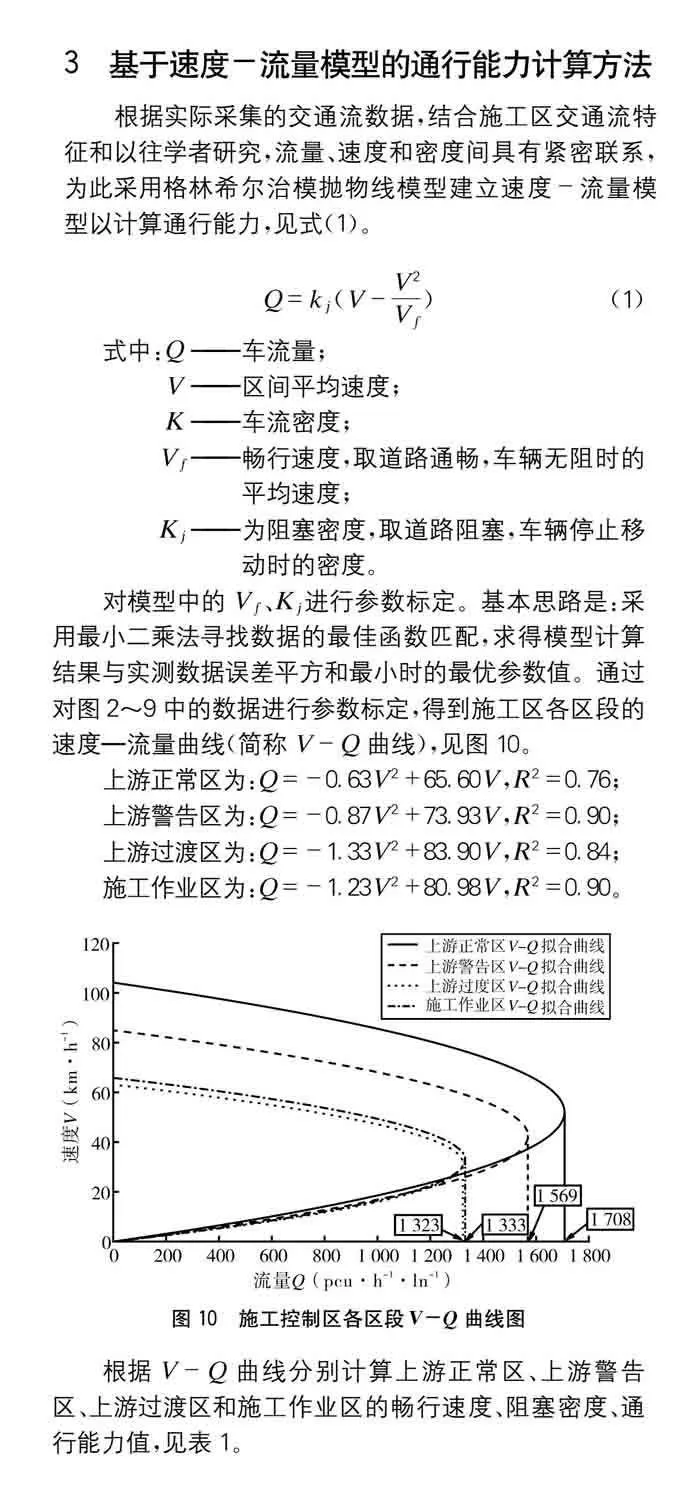
對模型中的Vf、Kj進行參數標定。基本思路是：采用最小二乘法尋找數據的最佳函數匹配，求得模型計算結果與實測數據誤差平方和最小時的最優參數值。通過對圖2～9中的數據進行參數標定，得到施工區各區段的速度—流量曲線（簡稱V-Q曲線），見圖10。

上游正常區為：Q=-0.63V2+65.60V，R2=0.76；

上游警告區為：Q=-0.87V2+73.93V，R2=0.90；

上游過渡區為：Q=-1.33V2+83.90V，R2=0.84；

施工作業區為：Q=-1.23V2+80.98V，R2=0.90。

根據V-Q曲線分別計算上游正常區、上游警告區、上游過渡區和施工作業區的暢行速度、阻塞密度、通行能力值，見表1。

4 基于影響因素修正模型的通行能力計算方法

結合本文實際道路情況、交通情況和美國HCM2000，主要影響因素有車速限制、行車道數、車道寬度和路側凈空、大型車混入率、駕駛員對環境的熟悉程度等，其他因素影響微弱可以忽略不計，由此，可確定影響因素修正的通行能力模型，見式（2）。

C=C0×fW×fHV×fP×n

（2）

式中：C——施工區通行能力（pcu·h-1·ln-1）；

C0——高速公路單車道基本通行能力（pcu·h-1·ln-1）；

fw——車道寬度及側向凈寬修正系數；

fHV——大型車修正系數；

fP——駕駛員對環境熟悉程度修正系數；

n——行車道數。

4.1 高速公路單車道基本通行能力（C0）

高速公路單車道基本通行能力是指在理想的道路（車道寬3.75 m，均為小客車），通過高速公路某一斷面或某點的最大小時流率，本文采用《公路工程技術標準》（JTGB01-2014）（以下簡稱《標準》）中的取值，見表2。施工時會根據實際情況對各施工作業區段進行限速，本文以區段內車輛的暢行速度作為其基本通行能力的設計車速，對表2的數據采用內插法進行確定。

4.2 車道寬度及側向凈寬修正系數（fw）

車道寬度和車道側向凈寬對于通行能力有很大的影響，需要根據實際情況對其影響大小進行劃分，可按表3進行取值。

4.3 大型車混入率修正系數（fHV）

車輛是交通的重要組成部分，不同類型的車具有不同的體積、行駛速度、道路空間占有率、車頭時距等，在對該因素定量時，需要對車輛類型進行細分。大型車混入率修正系數采用HCM2000推薦的計算公式。

fHV=11+∑pi（Ei-1）

（3）

式中：fHV——大型車混入率修正系數；

Pi——i類型車輛交通量占總交通量的百分比；

Ei——i類型車輛換算成標準車型的車輛折減系數。

取小客車作為標準車車型，其他不同類型車輛的折減系數取值依據《標準》，見表4。

4.4 駕駛員適應性修正系數（fP）

通過分析駕駛員技術的嫻熟程度、對交通法規的遵守程度、開車過程中的身體狀態等方面，對該系數進行確定，在0.9～1.0取值。考慮到越靠近施工區對駕駛員的影響越大，靠近施工區段的修正系數應降低。

通過實測數據確定各施工控制區的基本通行能力和修正系數，上游正常區基本通行能力為2 106 pcu·h-1·ln-1，fw、fHV、fP分別為1、0.84、0.97；上游警告基本通行能力為2 121 pcu·h-1·ln-1，fw、fHV、fP分別為1、0.84、0.95；上游過渡區基本通行能力為1 863 pcu·h-1·ln-1，fw、fHV、fP分別為0.93、0.84、0.92；施工作業區基本通行能力為1 866 pcu·h-1·ln-1，fw、fHV、fP分別為0.93、0.87、0.92。使用影響因素修正模型可計算出各區段的通行能力值。

（1）上游正常路段：2 106×1×0.84×0.97=1 716（pcu·h-1·ln-1）；

（2）上游過渡段：2 021×1×0.84×0.95=1 612（pcu·h-1·ln-1）；

（3）上游警告段：1 863×0.93×0.84×0.92=1 339（pcu·h-1·ln-1）；

（4）施工作業段：1 866×0.93×0.87×0.92=1 389（pcu·h-1·ln-1）。

5 兩種通行能力確定方法的比較

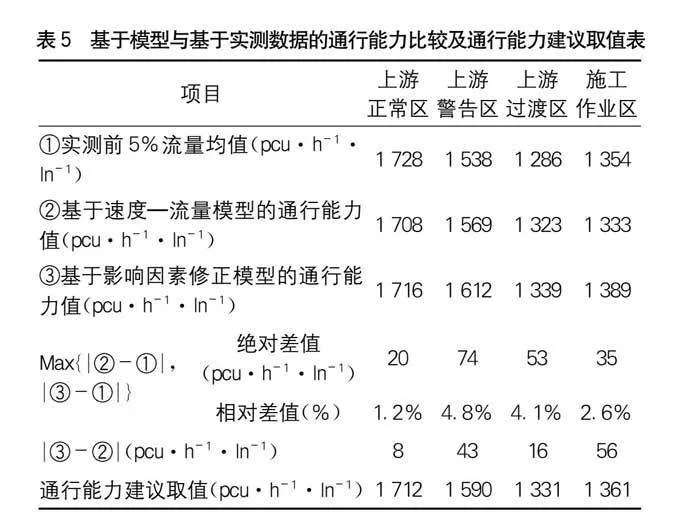
前文為了確定施工作業控制區主要區段通行能力，采用了兩種方法：（1）通過對采集的交通流數據進行曲線擬合，得到速度-密度的流量模型，計算出通行能力值；（2）根據實際道路參數確定基本通行能力，再利用改擴建時的主要交通流影響因素對其進行修正，計算通行能力值。下面將這兩種方法的結果與實測數據的前5%流量的平均值進行對比，結果見下頁表5。

由表5可知，基于影響因素修正模型計算的結果比基于速度-流量模型計算的結果稍大，兩種通行能力計算模型計算結果的最大絕對差值為56 pcu·h-1·ln-1，在可接受的范圍內。兩種通行能力計算模型計算的結果與實測數據相比較，最大絕對差值為74 pcu·h-1·ln-1，最大相對差值為4.8%，可見這兩種方法都能用于計算施工控制區的實際通行能力值，最終取兩種方法的平均值作為通行能力推薦值。

6 結語

本文對高速公路改擴建施工區交通控制段交通特征進行了分析，發現在上游過渡區因為存在大量的換道行為，導致交通流往往在交通量到達1 000 pcu·h-1·ln-1時就發生擁堵，小于實測交通量最大值1 328 pcu·h-1·ln-1。因此，上游過渡區是施工控制區的瓶頸段，在進行施工交通規劃中應重點關注。

基于速度-流量以及基于影響因素修正的通行能力模型對改擴建施工區各主要區段的通行能力計算都具有很好的準確性，模型計算結果與實測最大交通量的相對誤差＜5%。取這兩種模型計算結果的平均值作為通行能力推薦值，上游正常區、上游警告區、上游過渡區、施工作業區的通行能力推薦值分別為：1 712 pcu·h-1·ln-1、1 590 pcu·h-1·ln-1、1 331 pcu·h-1·ln-1、1 361 pcu·h-1·ln-1。

參考文獻

［1］Ye X，Chen Y，Chen C.Study on traffic organization and work-zone optimization of four-lane freeway reconstruction and expansion［J］.Journal of Physics：Conference Series，2019（1187）：052102.

［2］Benekohal R，Kaja-Mohideen A Z，Chitturi M.Methodology for Estimating Operating Speed and Capacity in Work Zones［J］.Transportation Research Record Journal of the Transportation Research Board，2004，1883（1）：103-111.

［3］唐 智，李細偉.高速公路通行能力分析［J］.公路，2012（5）：279-281.

［4］Yeom C，Hajbabaie A，Schroeder B J，et al.Innovative Work Zone Capacity Models from Nationwide Field and Archival Sources［J］.Transportation Research Record Journal of the Transportation Research Board，2015（2 485）：51-60.

［5］魏雪延，徐鋮鋮，王 煒，等.多車道高速公路的通行能力分析與建模［J］.交通運輸系統工程與信息，2017，17（2）：105-111.

［6］劉偉銘，梁 雪.交通事故下高速公路有效通行能力分析與估算［J］.科學技術與工程，2018（18）：112-117.

［7］Jehn N L，Turochy R E.Calibration of Vissim Models for Rural Freeway Lane Closures：Novel Approach to the Modification of Key Parameters［J］.Transportation Research Record Journal of the Transportation Research Board，2019，2 673（4）：036119811984282.

［8］Bian Z，K Ozbay.Estimating Uncertainty of Work Zone Capacity using Neural Network Models［J］.Transportation Research Record Journal of the Transportation Research Board，2019（2）：49-59.

［9］薛行健，戈林娟，鄧力容，等.快速路匝道合流區流量、加速車道長度與通行能力關系［J］.鐵道科學與工程學報，2020（2）：509-515.

［10］孟祥海，張龍釗，李生龍.四車道高速公路部分占用超車道交通控制區交通特性及通行能力研究［J］.交通運輸系統工程與信息，2020（2）：218-224.

［11］邵長橋，黃群龍.高速公路改擴建施工區交通流特性［J］.北京工業大學學報，2021（9）：1 036-1 047.

［12］宋婉璐，韓寶睿，張夢凡，等.基于瓶頸段會車約束性的窄雙車道公路通行能力分析［J］.公路，2021（6）：227-232.