預應力混凝土連續梁橋轉體施工中的穩定性分析與控制

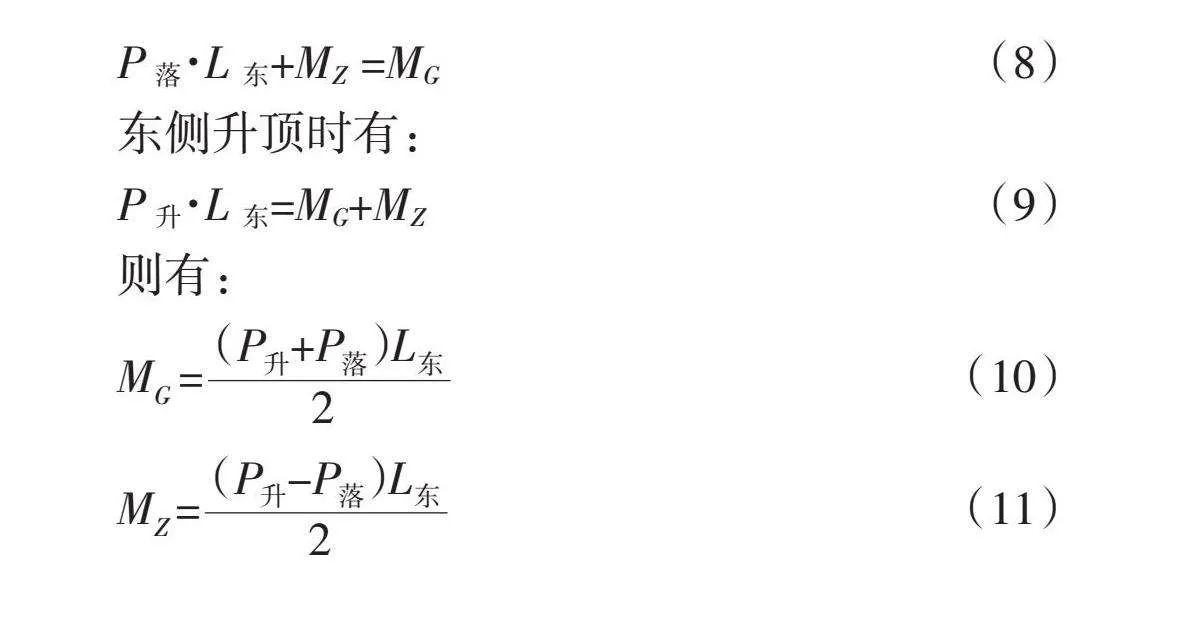
摘要：本文針對跨越207省道及既有隴海鐵路的轉體連續梁展開了系統的研究。通過數值模擬與試驗相結合的方法，探討其在加速和勻速轉動過程中結構的穩定性和應力分布特性。分析了不同轉動速度與加速度對主梁受力狀態的影響，得出了材料在承載力達到臨界值后的變形行為。強調了施工過程中控制荷載施加的必要性，防止因超出抗拉強度而導致的結構損壞。結果表明：隨著荷載的增加，主梁的變形由彈性逐漸轉向非線性，應力集中現象可能會對結構造成局部損傷。因此，在工程實踐中需采取監測手段，實時追蹤變形情況，以制定有效的控制策略。本研究為轉體連續梁的安全施工和設計提供了堅實的理論基礎和實用的數據支持。

關鍵詞：預應力混凝土；連續梁橋；球鉸轉動法；穩定性分析

中圖分類號：U448.215"" 文獻標識碼：A"" 文章編號：2096-2118（2024）06-0067-07

Stability Analysis and Control in the Rotating Construction

of Prestressed Concrete Continuous Girder Bridge

FU Lin

（China Railway 14th Bureau Group Corporation Limited，Jinan Shandong 250014，China）

Abstract：A systematic study is carried out on the rotating continuous girder spanning 207 provincial highways and the existing Longhai Railway.The stability and stress distribution characteristics of the structure is investigated in the process of acceleration and uniform rotation through the combination of numerical simulation and test.The effects of different rotation speeds and accelerations on the force state of the main girder are analyzed，and the deformation behavior of the material after the bearing capacity reaches the critical value is derived.Emphasizing the necessity of controlling the load application during the construction process to prevent the structural damage due to exceeding the tensile strength.It is revealed that the deformation of the main girder gradually shifts from elasticity to nonlinearity as the load increases，and the stress concentration phenomenon may cause localized damage to the structure.Therefore， monitoring means are required to track the deformation in real time in order to formulate an effective control strategy in engineering practice.This study provides a solid theoretical foundation and practical data support for the safe construction and design of rotating continuous girders.

Keywords：prestressed concrete；continuous girder bridge；ball-hinge rotation method；stability analysis

隨著交通運輸業的快速發展，基礎設施建設尤其是橋梁的需求日益增加。預應力混凝土連續梁橋因其良好的承載能力、較大的跨越能力以及優雅的外觀而成為現代橋梁工程中廣泛應用的一種結構形式。在復雜的施工環境和不斷變化的荷載條件下，這些橋梁在施工過程中的穩定性顯得尤為重要。特別是在橋梁的旋轉施工過程中，如何保證結構的穩定性，是確保橋梁安全性和施工精確性的關鍵。旋轉施工技術具有施工作業面小、施工周期短等優點。然而，在實際施工過程中，梁體在旋轉階段所承受的動態荷載、摩擦力和不平衡力矩等因素對結構的穩定性形成了嚴峻挑戰。針對這些問題，進行深度的穩定性分析與有效的控制措施，旨在確保每一次的旋轉都能成功且安全地完成，是當前橋梁工程領域亟需解決的重要課題。

近年來，國內外學者紛紛關注預應力混凝土連續梁橋的旋轉施工技術及其穩定性研究。國外在這方面起步較早，相關研究涵蓋了旋轉過程中的力學模型、數值模擬和實驗研究等方面。盡管國內該技術起步較晚，但建造的轉體施工橋梁數量和寬度已超國外，取得了顯著的社會、環境和經濟效益[1]。隨著橋梁工程技術的發展，越來越多的研究開始關注預應力混凝土連續梁橋的旋轉施工。此外，基于球鉸轉動法的研究也逐漸受到重視，該方法能夠更精準地計算不平衡力矩，從而為施工提供更加可靠的理論指導。

梁體的穩定是轉動的必要條件，對于大跨度轉體懸臂結構，轉體前需設置5 cm～15 cm的預偏量來保持轉體體系的穩定性，對于不同轉動體系橋梁結構預偏量的設置需通過轉體稱重試驗來確定[2]。球鉸是橋梁轉動支撐體系的關鍵，轉動面摩擦力決定轉動牽引力的大小[3]。盡管我國在預應力混凝土連續梁橋旋轉施工方向的研究已取得了一些進展，但是目前的研究多集中于靜態穩定性，忽視了動態條件下的穩定性分析，不能全面評估旋轉過程中的風險。對于旋轉過程中的動態行為分析仍有待提高，特別是在各種荷載作用下，梁體的動態響應特征尚不明晰。此外，在復雜工況下對轉體梁研究較少，缺乏對轉體速度、加速度等參數在不同環境條件下的定量化影響分析。

綜上所述，針對預應力混凝土連續梁橋旋轉過程中的穩定性分析與控制還需深入研究。本文旨在結合理論計算與實測數據分析，明確旋轉過程中的關鍵參數，并探索有效的穩定性控制措施，系統探討了加速和勻速轉動過程中結構的穩定性和應力分布特性，彌補了動態施工工況下非線性行為研究的不足，以期提高橋梁施工的安全性與精確性。針對復雜工況提出具體分析，擴展了轉體梁研究的適用性，為類似工程提供了可靠參考。

1 模型的建立

1.1 工程概況

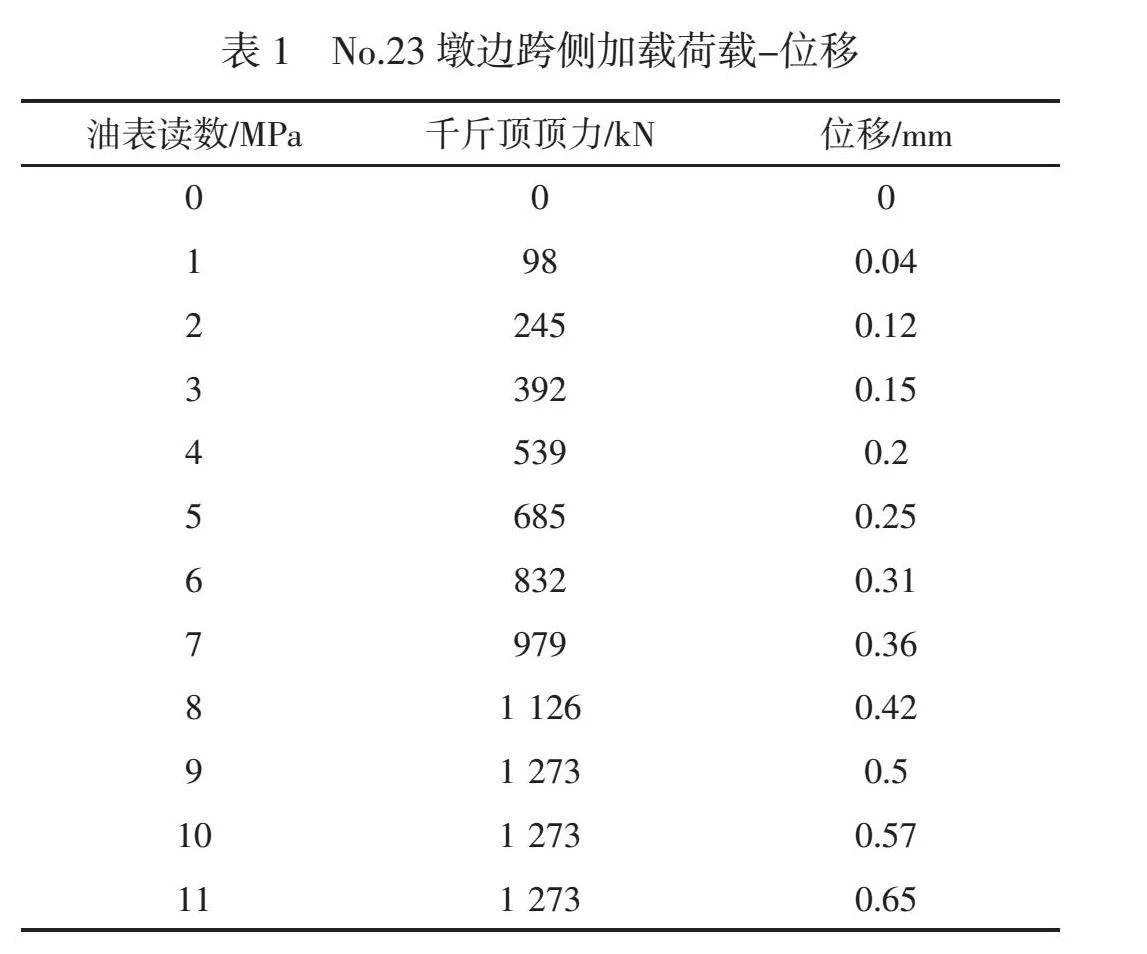
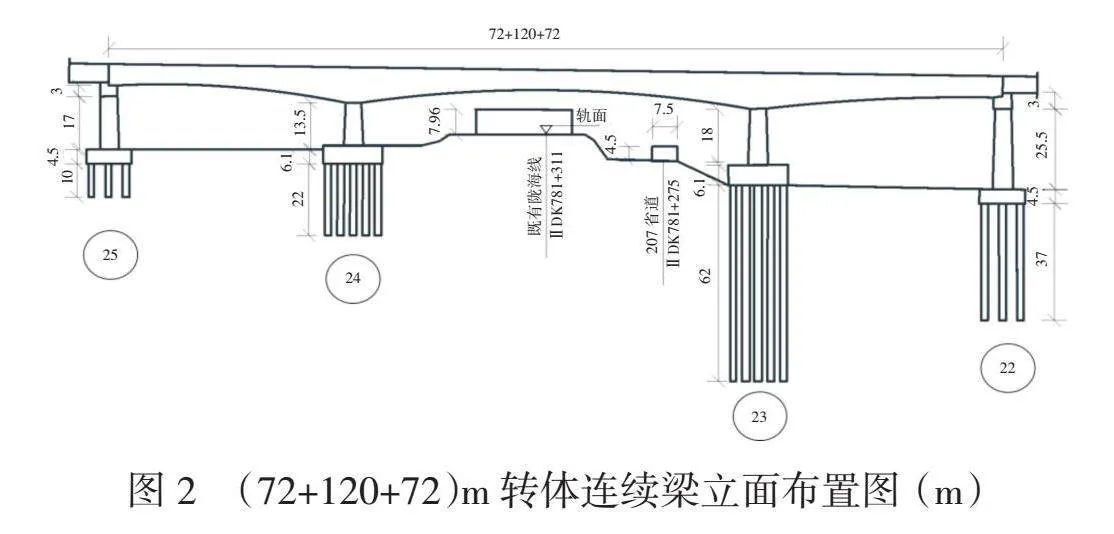
本文研究對象為跨越207省道及既有隴海鐵路的（72+120+72）m轉體連續梁，轉體重量約為12 000 t。轉體連續梁實景和立面布置見圖1～圖2。

1.2 有限元模型建立

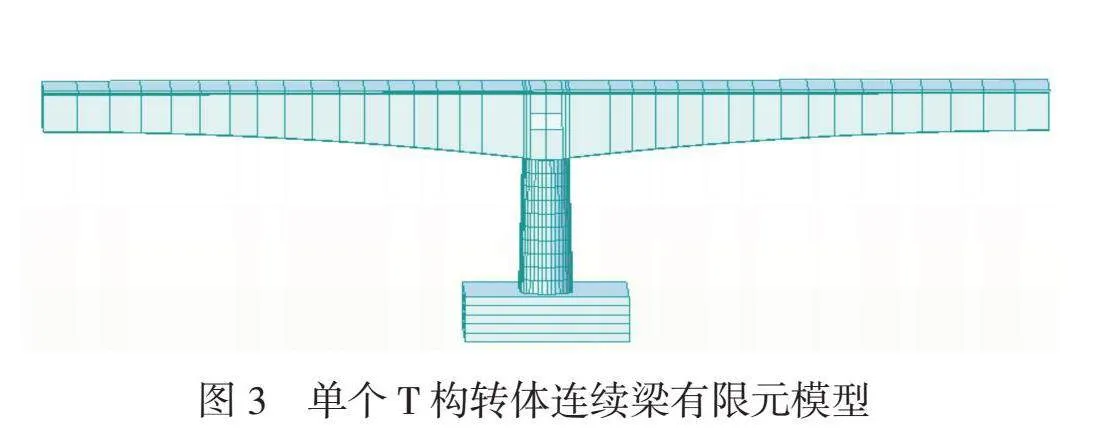
采用Midas Civil分析軟件進行建模，含梁體、橋墩及承臺的單個T構轉體連續梁有限元模型如圖3所示，共計54個梁單元，支座與梁體采用彈性剛性連接。橋梁轉體過程通常有加速、勻速、減速、點動4個階段，加速與減速階段是對稱的階段，同時該工程在實際施工時沒有點動階段，故本文僅對加速與勻速階段的受力進行分析。

1.3 數學模型的建立

橋梁從靜止狀態達到勻速狀態時，則牽引力需大于轉動轉盤的摩擦力。因此，橋梁會有一個加速轉動的過程，然后才能達到勻速狀態。當橋梁接近預設位置時，會有相應的減速過程，從而使橋梁靜止。加速與減速過程中對單個T構轉體連續梁的影響計算公式如下。

1） 單個T構轉體連續梁繞軸轉動時角動量為：

M=（1）

LZ=Jω（2）

M=J=Jα（3）

式（1）～式（3）中：MZ為單個T構轉體連續梁轉動的轉動力矩，kN·m；d為運算符；LZ為單個T構轉體連續梁轉動的角動量；t為時間，s；J為轉動慣量，kg·m2；ω是轉動的角速度，rad/s；α為橋體轉動的加速度，rad/s2。

扭轉最大剪應力為：

τ=（4）

W=（3h-b）-（3h-b）（5）

式（4）～式（5）中：WP為箱型截面的抗扭截面系數；bh，h分別為箱型截面的寬度、高度，m；bω，hω分別為截面孔洞的寬度、高度，m。

2） 不同加速度對橋體結構穩定性分析

結合施工圖和規范，混凝土抗拉值的計算公式為：

y≤1.89（6）

式（6）中：J取4.13×109 kg·m2，y為截面高度，取3.33 m，I為截面慣性矩，取243.11 m4。

當混凝土拉應力值為設計強度（1.89 MPa）時，可得球鉸的加速度為：

α=

=

=0.12 m/s（7）

1.4 模型驗證

基于上述建模方法和數學模型，通過李天平等[4]的研究結果對比驗證本文的建模方法，誤差lt;5%，證明了模型的準確性和適用性。

2 梁體穩定性分析

2.1 加速轉動時主梁穩定性分析

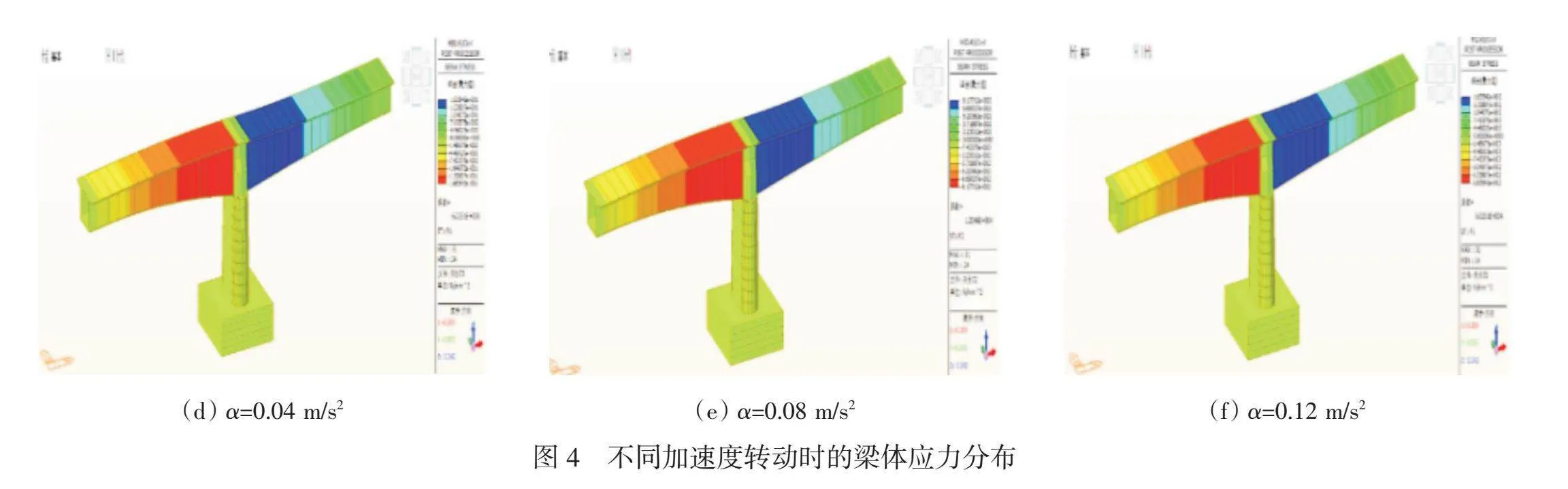
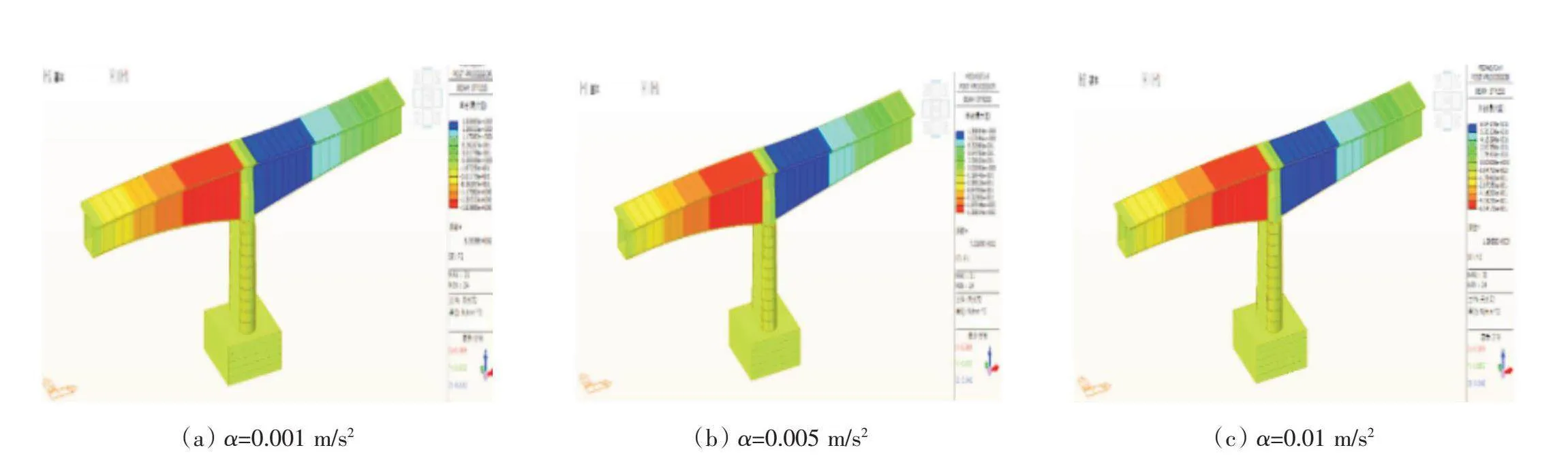
加速轉動過程中，結構承受的力和應力顯著增加，可能導致材料屈服或斷裂。穩定性分析有助于預測和避免災難性故障，從而保護人員和設備安全。非線性力學特性在轉體過程中可能引發局部應力集中和累積變形，增加結構失穩的風險。尤其在轉動加速階段，非線性力學特性對結構安全的影響更為顯著。六種工況以加速度不同作為區分，分別為0.001 m/s2，0.005 m/s2，0.01 m/s2，0.04 m/s2，0.08 m/s2，0.12 m/s2。通過對前文建立的含梁體、橋墩及承臺的單個T構轉體連續梁有限元模型的計算，得出不同加速度轉動時的梁體應力分布如圖4所示。

由圖4可知，最大拉應力出現在梁體根部，加速度為0.001 m/s2時，最大值為0.016 MPa；加速度為0.005 m/s2時，最大值為0.082 MPa；加速度為0.01 m/s2時，最大值為0.164 MPa；加速度為0.04 m/s2時，最大值為0.654 MPa；加速度為0.08 m/s2時，最大值為1.311 MPa；加速度達到0.12 m/s2時，最大拉應力達到混凝土抗拉極限應力值1.89 MPa。由以上梁體應力變化規律可知，轉體連續梁梁體拉應力隨著轉動加速度的增大而增大，當加速度達到0.12 m/s2，轉體連續梁根部混凝土拉應力達到極值，若超過該數值梁體混凝土會因抗拉強度不足而遭到破壞。在動態施工工況下，非線性力學特性與慣性力的耦合作用會進一步影響轉體連續梁的安全性，適當減小轉體加速度并優化荷載分布策略，可以顯著降低因非線性行為引發的安全隱患。

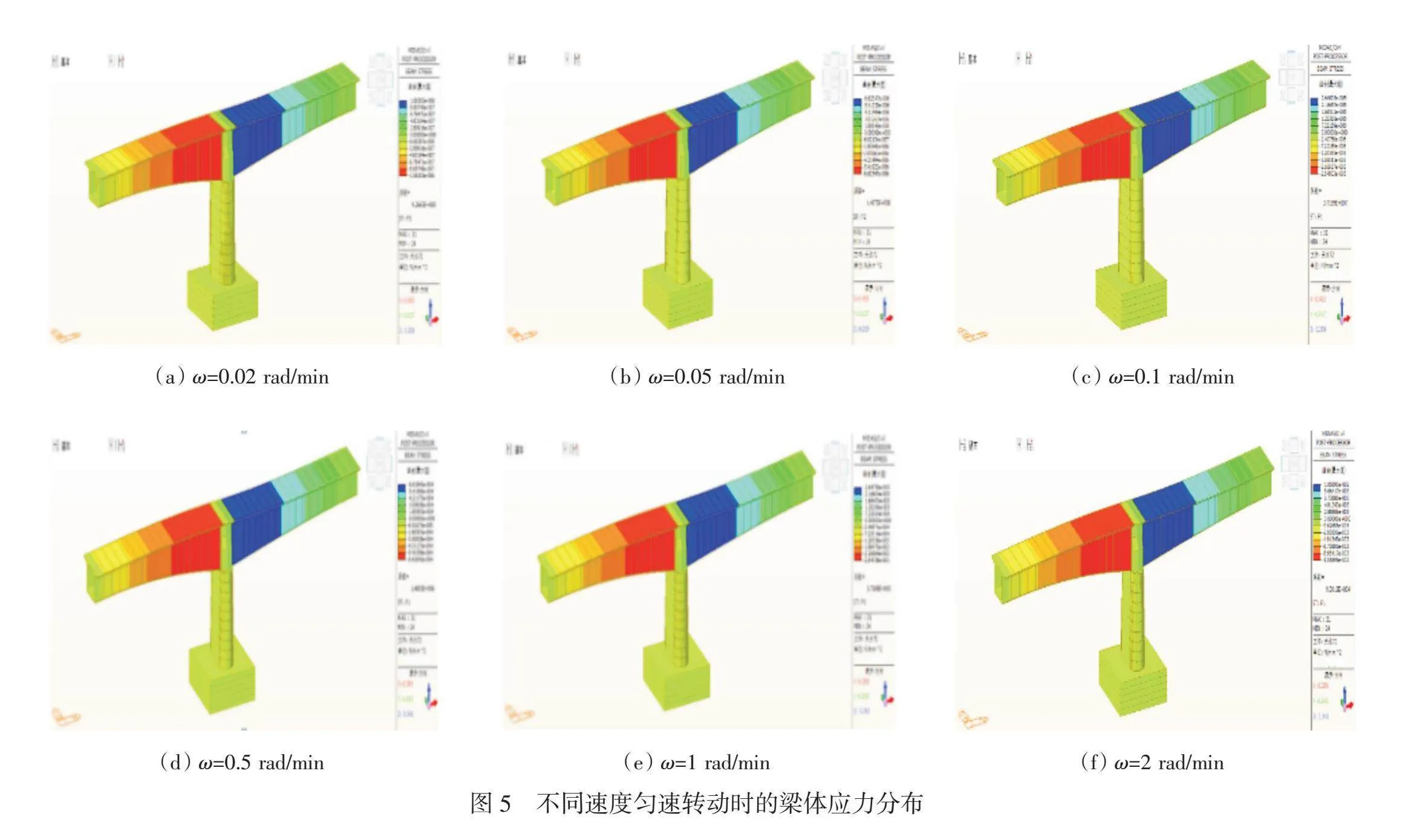
2.2 勻速轉動時主梁穩定性分析

由于轉動過程中勻速轉動時間最長，假設轉速分別為0.02 rad/min，0.05 rad/min，0.1 rad/min，0.5 rad/min，1 rad/min，2 rad/min的六種工況進行分析，分析結果見圖5。

由圖5可知，最大拉應力同樣出現在梁體根部，轉動速度為0.02 rad/min時，最大拉應力為1.06×10-6 MPa；當轉動速度為0.05 rad/min時，最大拉應力為6.62×10-6 MPa；當轉動速度為0.1 rad/min時，最大拉應力為2.65×10-5 MPa；當轉動速度為0.5 rad/min時，最大拉應力為6.62×10-4 MPa；當轉動速度為1 rad/min時，最大拉應力為2.65×10-3 MPa；當轉動速度為2 rad/min時，最大拉應力為1.06×10-2 MPa。由此可得，在施工轉體時，轉速不得超過0.02 rad/min。相比加速度對梁體的應力影響而言，勻速轉動對結構影響不大。

3 球鉸轉動法

3.1 基本原理

1） 不平衡力矩測試方法及分析

橋梁脫架后懸臂結構有兩種平衡狀況，設摩阻力矩為MZ，kN·m；不平衡力矩為MG，kN·m。

平衡狀況一： MZ lt;MG

轉體結構重心偏東邊跨時：

東側落頂時有：

P落·L東+MZ =MG（8）

東側升頂時有：

P升·L東=MG+MZ（9）

則有：

M=（10）

M=（11）

式（8）～式（11）中：P落，P升分別為微小轉動時的支撐力，kN；L東，L西分別為東、西側支點距離，m。

平衡狀況二： MZgt;MG

假設條件與狀況一相同，

從東側頂梁時

P東·L東=MG+MZ（12）

從西側頂梁時

P西·L西+MG=MZ（13）

則有

M=（14）

M=（15）

式（12）～式（15）中：P東，P西分別為微小轉動時東、西方向的支撐力，kN。

2） 靜摩擦系數分析計算

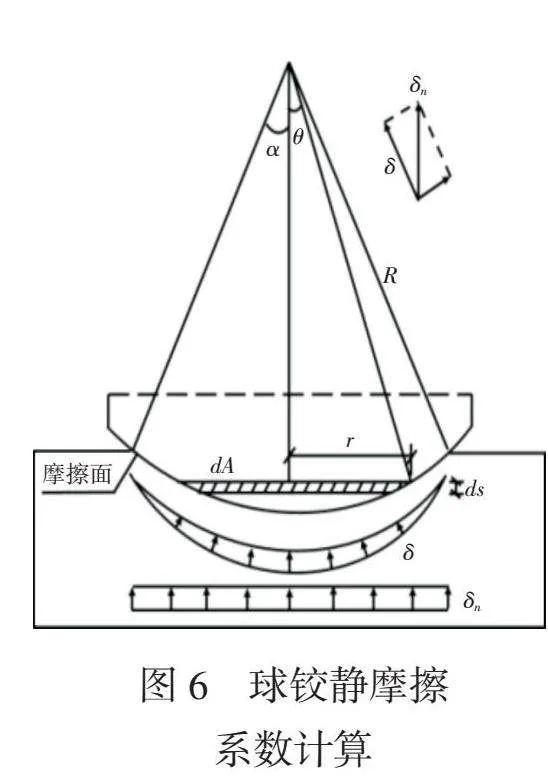
圖6為球鉸靜摩擦系數計算，球鉸轉動面上的摩阻系數和偏心距的計算過程如下[5]：

由于

dMZ=RcosθdF，dF=μ0 σdA，dA=2πrds，r=Rsinθ，

ds=Rdθ，σ=σcosθ，σ=

則dM=dθ

M=dM=μNR（16）

得球鉸靜摩阻系數：

μ=×（17）

轉動體偏心矩為：

e=MG /N（18）

式（18）中：N為轉體重量，t。

3.2 稱重試驗各項參數估算

μ=×（19）

式（19）中：R為球鉸球徑，取8 m；N取12 000 t。

依據經驗可得摩阻系數μ值約為0.02～0.04，故假設μ=0.03，得到MZ =28 379 kN·m。

MZ =（F左L左+F右L右）/2（20）

假設F左=F右，L左=L右，取L=5.5 m，計算得F=5 159.82 kN，由此得到稱重頂力為5 200 kN。

3.3 測點布置及數據采集

在轉體前稱重測點的布置，按照測量方便、實測數據具有一定代表性和說服力的原則進行布置，如圖7所示。

3.4 試驗數據分析及結果

3.4.1 No.23墩

1） 邊跨側試驗結果

荷載-位移關系曲線測試結果見表1，千斤頂定力數值lt;1 126 kN時，荷載-位移呈非線性相關關系，這是由于在這一階段，主梁的剛度較高，能夠有效地承受加載而不發生明顯的變形。隨著荷載的不斷增加，材料內部微觀結構開始逐步響應外部應力，出現局部的塑性區域。千斤頂定力數值gt;1 126 kN時，主梁的受力狀態趨于均勻，塑性變形主要集中在梁的截面上，導致變形速率與荷載成正比，從而形成線性關系。由此可知P1=1 126 kN。

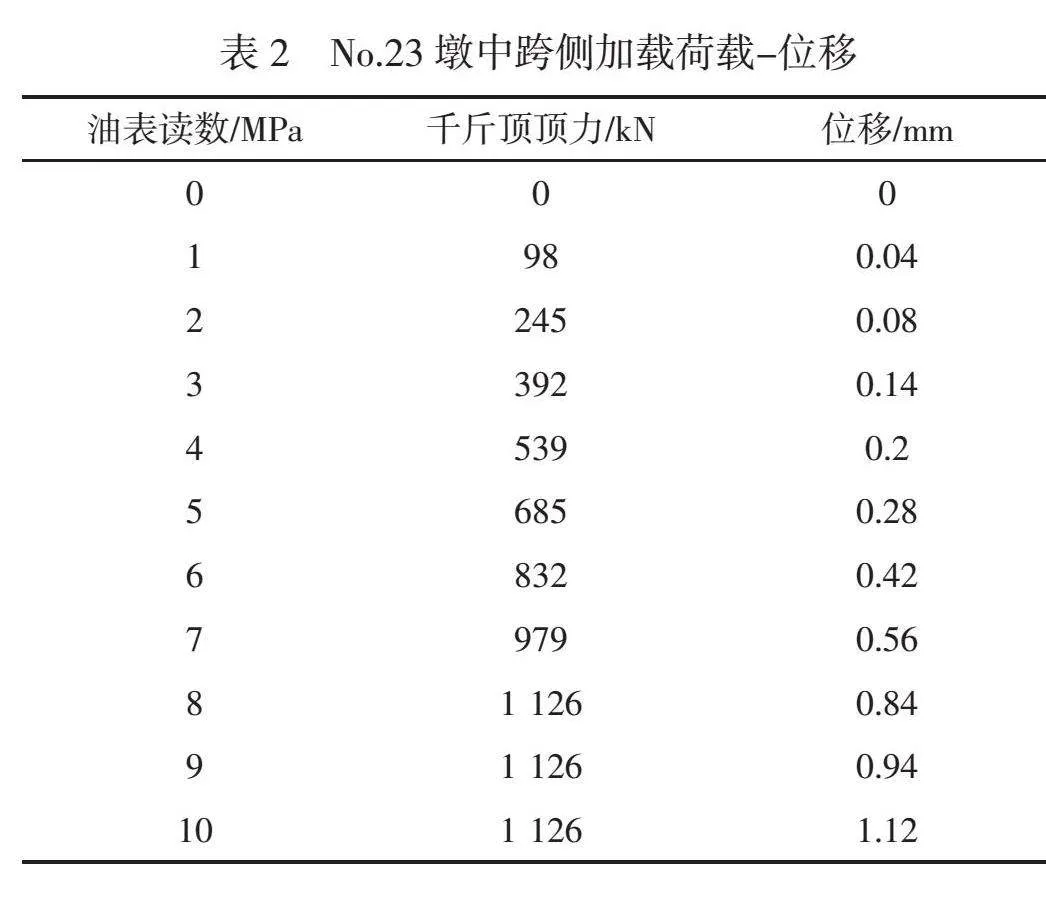
2） 中跨側試驗結果

荷載-位移試驗結果見表2，千斤頂定力數值lt;753 kN時，結構主要處于彈性狀態，材料表現出較大的初始剛度。隨著荷載逐漸增加，材料內的微觀結構逐步響應外部應力，導致位移增量相對較小。千斤頂定力數值gt;753 kN時，材料的受力狀態以塑性變形為主導，遵循線性應力-應變關系，符合胡克定律。由此可知P2=753 kN。

3.4.2 No.24墩

1） 邊跨側試驗結果

荷載-位移試驗結果見表3，千斤頂定力數值lt;1 872 kN時，荷載施加后，結構內部的應力分布往往不均勻，局部區域可能會出現更大的變形，這導致整體荷載與位移之間的關系曲線呈現非線性。千斤頂定力數值gt;1 872 kN時，結構中的塑性區逐漸擴大，應力在整個材料中趨于均勻分布。這使得額外的荷載能夠以線性方式傳遞，并導致較快的位移增量。由此可知P2=1 872 kN。

2） 中跨側試驗結果

荷載-位移試驗結果見表4，千斤頂定力數值小于lt;材料自身特性，可能存在微小的塑性變形情況。千斤頂定力數值gt;1 273 kN時，盡管材料仍能承載更大的荷載，但因塑性變形的發生，有效剛度會隨著荷載的增加而減小。此時，荷載增加導致的位移增量則以線性方式上升。由此可知P2=1 273 kN。

由表1～表4可知，保持梁體平衡狀態時球鉸摩阻力矩不得小于轉動體系的不平衡力矩，因此，不平衡力矩：

M=（21）

摩阻力矩：

M=（22）

球鉸靜摩阻系數：

μ=（23）

轉動體偏心距：

e=（24）

不平衡力矩是指作用在轉動體上的各種力的合成所產生的力矩。在保持梁體平衡的情況下，不平衡力矩必須由球鉸摩阻力矩來抵消，以確保結構穩定。球鉸摩阻力矩則依賴于靜摩擦系數和偏心距，起到抵抗不平衡力矩的作用。由表5～表6的計算結果顯示了不同墩的轉動體參數。通過對比可以發現，當施加荷載（P1和P2）不同時，其不平衡力矩（MZ）也隨之變化。雖然兩個墩的摩阻力矩都能夠滿足相應的不平衡力矩，但需要注意的是，隨著荷載的增加，摩擦系數的線性假設可能不再有效，特別是在材料疲勞或磨損的情況下。在設計轉動體系時，應確保摩阻力矩始終≥不平衡力矩，以確保結構的長期穩定性。同時，應考慮摩擦系數的變動帶來的潛在影響，進行適當的安全裕度設計。

4 討論

4.1 環境因素對混凝土性能的潛在影響

溫度和濕度是影響混凝土性能的重要環境因素，尤其在復雜施工工況下，這些因素可能對材料的強度、變形和裂縫擴展產生顯著作用。在高溫環境中，混凝土內部水分蒸發可能導致干縮變形加劇，進一步加速裂縫的形成。而在高濕度或低溫環境下，混凝土的硬化速度和強度發展規律會發生變化，影響其承載性能。

4.2 環境因素對轉體施工的影響分析

轉體連續梁施工過程中，溫度梯度可能引起主梁內部應力分布的不均勻性，進而影響其整體受力特性和轉動穩定性。同時，濕度變化會通過改變混凝土的收縮與膨脹行為，間接影響主梁的變形與應力集中。本文強調在實際施工中應充分考慮環境因素的變化，以降低其對施工安全的潛在風險。

4.3 工程實踐建議

為降低環境因素的不利影響，建議在施工過程中采取以下措施：①在施工方案中加入溫濕度的監測與調整預案，例如利用遮陽、噴霧等手段控制施工環境條件；②對混凝土配合比進行適當調整，以提高其在極端環境下的性能穩定性；③在施工過程中設置溫濕度應力監測點，實時跟蹤環境參數與結構響應的變化，確保施工安全。

基于成本效益分析的結果，本文提出以下建議：①在施工方案中引入成本與周期評估機制，平衡效率與安全性；②針對加速度和轉動速度的選擇，結合具體工程條件，優先選取性價比較高的參數；③利用實時監測系統跟蹤施工進度與成本消耗，動態調整施工速度以應對突發情況。

5 結論

本文針對跨越207省道及既有隴海鐵路的轉體連續梁進行了全面的有限元模型分析和稱重試驗，通過數值模擬與實際測試相結合的方法，得出以下結論。

1） 結構的受力特性與轉動速度和加速度密切相關。在千斤頂施加荷載過程中，不同的荷載水平導致了材料狀態的變化，特別是在超過一定臨界荷載后，材料內部開始出現塑性區域，從而影響整體結構的剛度和穩定性。

2） 確定了不同跨距下的關鍵荷載值的具體數值。當千斤頂定力達到850 kN時，主梁進入均勻受力的階段，而中跨試驗則顯示600 kN為臨界點。

3） 隨著荷載的增加，主梁的變形表現逐漸由彈性轉為非線性，這一現象在工程設計中必須予以重視。特別是在梁體承受較大荷載時，其變形速率顯著增加，可能會引發局部的應力集中，進而導致結構損傷。因此，在實際施工操作中，應當采取適當的監測手段，對變形情況進行實時監控，并制定有效的控制方案，以確保施工過程的安全性。

4） 未來研究的方向可以進一步拓展至轉體橋梁在不同環境條件下的性能評估，例如溫度、濕度等因素對材料性能的影響。此外，可以考慮對更復雜的操作，如梯級加速進行深入研究，以優化設計方案，從而提升類似工程的安全實施效率。

參 考 文 獻

[1]董月龍.公跨鐵2×65 mT構轉體橋梁設計與荷載敏感性分析[J].工程建設與設計，2022（21）：65-69.

[2]楊乃濤.大噸位預應力混凝土T型剛構橋梁轉體施工技術研究[D].西安：長安大學，2017.

[3]趙青.橋梁工程的轉體施工技術[J].交通世界（運輸·車輛），2015（8）：60-61.

[4]李天平，李文洲.大跨橋梁轉體系統中球鉸接觸面應力計算[J].蘭州理工大學學報，2023，49（4）：122-128.

[5]劉濤.大跨徑橋梁轉體施工混凝土球鉸關鍵問題研究[D].武漢：武漢理工大學，2018.

編輯：劉 巖