與圓模型有關的最值問題及其解題策略

【摘要】動點軌跡問題是中考和各類模擬考試的重點和難點題型，綜合考查了學生的幾何知識和思維能力.其中，動點軌跡為圓的最值問題具有一定的難度，致使該題型成為學生在中考中失分的集中點.掌握軌跡為圓的幾種模型，并構建問題解決的一般思路，是應對中考與圓有關的動點問題的一個重要途徑.文章就動點軌跡為圓（圓弧）的模型進行梳理，并給出相應的解題策略，旨在為一線教師在中考備考復習中提供教學參考.

【關鍵詞】動點問題；定義模型；直角模型；等弦對等角模型；最值問題

引 言

與動點有關的最值問題，是中考的一個難點.如果學生能確定動點的運動軌跡，然后結合軌跡的幾何性質求解，會事半功倍.下面介紹動點軌跡為圓（圓弧）的三種模型，并結合中考題給出每種模型的解題策略.

一、動點軌跡為圓（圓弧）的三種模型

模型1 定義型

如圖1所示，設點A為定點，點B為動點，若AB長度固定，則點B的軌跡是以點A為圓心，AB長為半徑的圓.

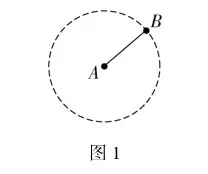
模型2 直徑所對的角為直角（直角模型）

一條定邊所對的角始終為直角，則直角頂點軌跡是以定邊為直徑的圓或圓弧.如圖2，若P為動點，AB為定值，∠APB=90°，則動點P的軌跡是以AB為直徑的圓或圓弧.

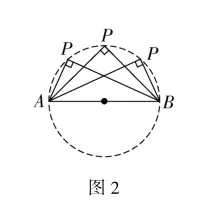
模型3 等弦對等角模型

一條定邊所對的角始終為定角，則定角頂點軌跡是圓弧.如圖3，若P為動點，AB為定值，∠APB為定值，則動點P的軌跡為圓弧.

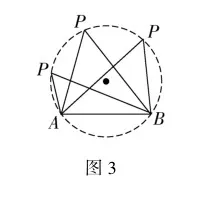
二、與圓有關的最值問題

1.定義型

該題型主要以選擇、填空形式出現，難度系數不大，在各類考試中都以中檔題為主.解這類問題的關鍵是結合圓的定義判定動點變化的特點，再結合圓的性質和其他幾何知識進行解題.

解題策略：

第一步：根據題意判定動點的變化特性；

第二步：找準定點和定長（圓心和半徑）；

第三步：結合圓、三角形、四邊形的相關知識進行解題.

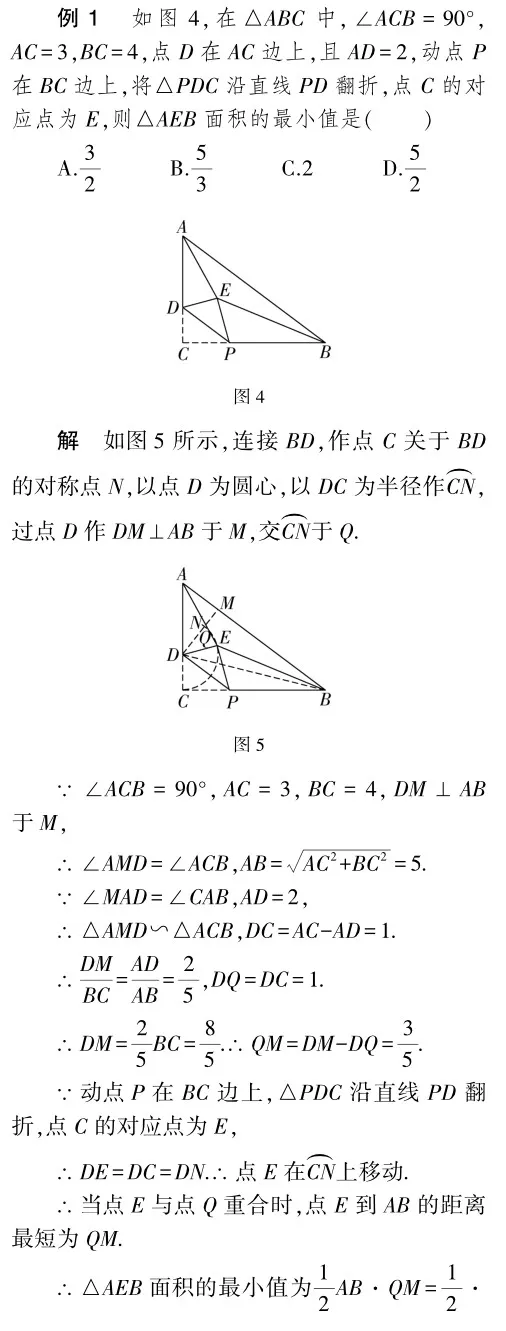
點評 本題考查勾股定理，相似三角形的判定定理和性質，軸對稱的性質，三角形面積公式，綜合應用這些知識是解題關鍵.先根據勾股定理及相似三角形的判定定理和性質求出DM的長度，再根據圓的性質求出QM的長度，判斷點E的運動軌跡，確定當點E與點Q重合時，點E到AB的距離最短為QM，再根據三角形面積公式求解即可.

2.直角模型

該題型主要以選擇、填空的形式出現，一般較為靠后，有一定難度.該題型主要考查對圓的性質的理解，有時會結合直角三角形的相關知識一起考查.利用數形結合思想，對圖形進行討論是解題的關鍵.

解題策略：

第一步：觀察圖形特點，找準直角頂點和定長（圓的直徑）；

第二步：利用圓與直角三角形的相關知識點進行解題；

第三步：涉及最值問題的圖形要考慮線段的轉化，熟練掌握共線問題、將軍飲馬問題、垂線段問題等相關知識點；

第四步：利用數形結合思想進行分析、解答.

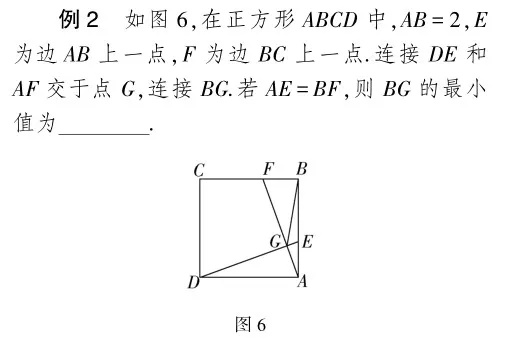
解 ∵四邊形ABCD是正方形，

∴∠ABF=∠DAE，AD=AB.

∵AE=BF，∴△DEA≌△AFB，

∴∠ADE=∠BAF，

∴∠DAF+∠BAF=∠DAB=90°，

∴∠ADE+∠DAF=90°，

∴∠DGA=90°，∴點G在以AD為直徑的圓上移動.

點評 根據SAS可證明△DEA≌△AFB，得∠ADE=∠BAF，再證明∠DGA=90°，進一步可得點G在以AD為直徑的半圓上，且O，G，B三點共線時BG取得最小值.

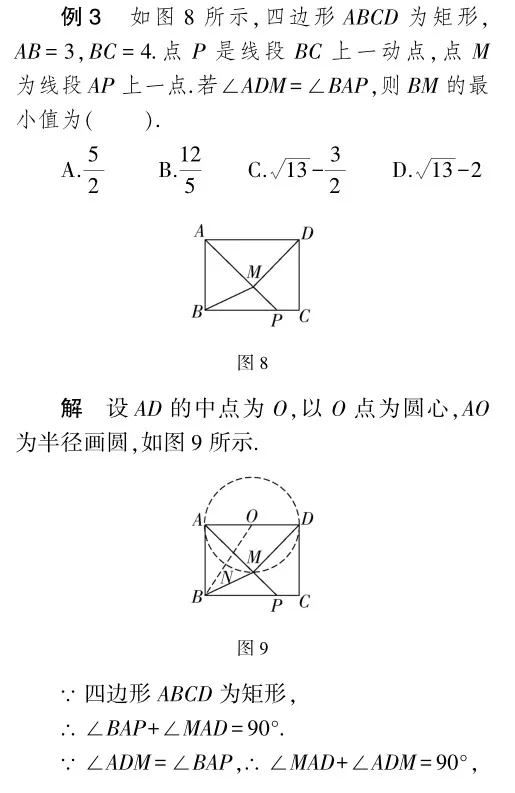
點評 本題的解題關鍵是熟練掌握直角三角形和圓的相關知識.證明∠AMD=90°，得出點M在以O點為圓心，AO為半徑的圓上，從而可計算出答案.

3.等弦對等角模型

該模型主要考查轉化與化歸的數學思想.常用到結論：一定點與圓上的動點距離最大值為定點到圓心的距離與半徑之和，最小值為定點到圓心的距離與半徑之差.

解題策略：

第一步：觀察圖形特點，確定定弦和定角；

第二步：根據題意準確分析出動點的運動軌跡，并構建適當圖形（三角形居多）；

第三步：利用四邊形、隱圓、直角三角形或相似的相關知識點解題.

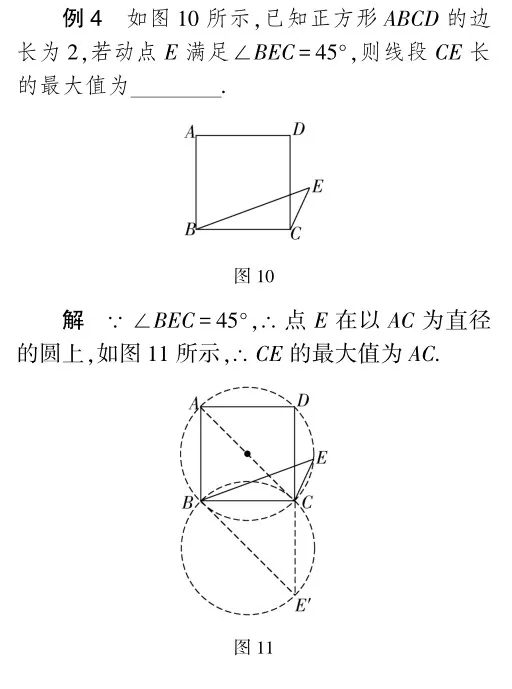
點評 本題主要考查圓周角定理、圓的基本性質及正方形的性質.根據題意得出點E是以AC為直徑的圓上的一個動點，根據最大的弦是直徑求得AC為CE的最大值，再利用勾股定理可得答案.

點評 本題考查全等三角形的判定和性質、等邊三角形的性質、圓、特殊角的三角函數等相關知識，解題的關鍵是學會添加輔助線.先證明∠APB=120°，推出點P的運動軌跡是以O為圓心，OA為半徑的弧.再連接CO交☉O于點P′，可知當點P運動到P′時，CP取到最小值.

結 語

與圓有關的最值問題往往涉及動點的軌跡，需要先判定動點的軌跡是否為圓（圓弧），然后利用圓的幾何性質及其他幾何知識求解.熟悉圓的以上三種模型及其相關的平面幾何知識是破解這類最值問題的關鍵.這類最值問題有一定的難度，主要考查化歸與轉化思想、數形結合思想的運用與邏輯推理能力等，是具有很好區分度和選拔功能的試題.一線教師在日常教學或者中考備考復習中要重視對這類最值問題的講解、歸納與總結.

【參考文獻】

[1]林紹隆.最值誠可貴，探究價更高：利用輔助圓求最值[J].理科考試研究，2021，28（2）：11-13.

[2]張劍.巧用隱圓解答初中數學最值問題[J].中學數學，2024（4）：51-52.

[3]王海軍.數學模型顯直觀 借圓助數促發展[J].高中數學教與學，2024（2）：44-46，53.