高中數學函數模塊教學策略探究

【摘要】函數作為數學課程的重要組成部分，在高中數學教學中占有關鍵地位.教師應堅持以探究、發展、繼承為主線，設計高效預習、形象教學、直觀分析、深化探究、遷移實踐、強化記憶、拓展學習等連貫的教學活動，使學生深刻地認識函數，并能靈活運用不同的函數模型解決實際問題.文章分析高中數學函數模塊的教學內容，提出探究性原則、發展性原則、繼承性原則，強調在承上啟下、銜接生活、技術賦能、問題導學、習題訓練、整體總結、滲透文化中組織具體教學，以供借鑒.

【關鍵詞】高中數學；函數；教學策略

引 言

高中數學課程內容突出函數、幾何與代數、概率與統計、數學建模活動與數學探究活動五條主線，要求教師從必修課程到選擇性必修課程、選修課程，全面把握四個維度的知識，發展學生的數學抽象、邏輯推理、數學建模、直觀想象等.具體的函數模塊，教學內容包括函數概念與性質、冪函數、指數函數、對數函數、三角函數、函數應用等，要求學生從基礎概念到綜合實踐，循序漸進地實現進階學習.教師應采取恰當的教學方法，提升高中數學函數模塊的教學質量.為此進行以下研究，首先詳細梳理高中數學函數模塊的教學內容，其次說明探究、發展、繼承的必要性，最后提出七個方面的具體策略.

一、高中數學函數模塊的教學內容

簡單來說，對于兩個變量x和y，如果每給定x的一個值，y都有唯一一個確定的值與其對應，那么就說y是x的函數.具體在數學角度進行描述，給定一個非空的數集A，對A施加對應法則f，記作f（A），得到另一數集B，記作B=f（A）.這個關系式就叫函數關系式，簡稱函數.

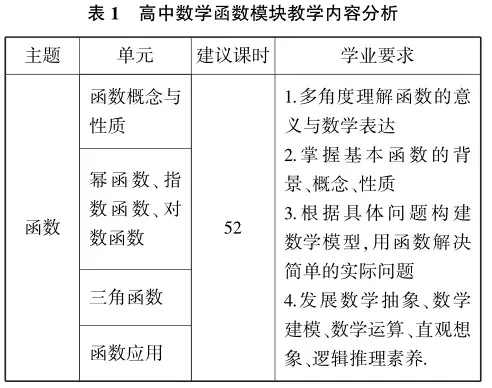
研讀《普通高中數學課程標準（2017年版 2020年修訂）》（下面簡稱《新課標》）可以發現，函數貫穿高中數學課程始終，包括函數的概念與性質、冪函數、指數函數、對數函數等，具體內容與課時安排可見表1.教師應充分重視高中數學函數模塊的教學活動，從基礎概念到綜合實踐，科學實施教學.

二、高中數學函數模塊的教學原則

高中數學課程提倡探究性學習，同時，在素質教育的背景下，高中數學教學應有利于學生的全面發展，使學生從不同方面提升核心素養水平.教師應具有整體意識，準備把握新舊知識的內在聯系，引導學生進行遷移學習.為此，具體在高中數學函數模塊教學中，教師應堅持探究性原則、發展性原則、繼承性原則.

（一）探究性原則

從兩個變量之間的依賴關系、實數集合間的對應關系、函數圖形的幾何直觀，多角度理解函數的意義與數學表達，理解函數符號表達與抽象定義之間的關聯，理解函數的單調性、最大（小）值、奇偶性、周期性等.對簡單的實際問題選擇適當的函數構建數學模型，從函數觀點認識方程、不等式，都需要進行充分的探究學習.故而在高中數學函數模塊教學中，教師應堅持探究性原則，鼓勵學生自主探究函數的概念與性質，區分冪函數、指數函數、對數函數等，打造生動活潑的探究型課堂.

（二）發展性原則

數學教育承載著落實立德樹人根本任務，發展素質教育的功能.高中數學函數模塊教學不僅應使學生掌握函數的基礎概念、具有綜合實踐能力，而且應關注學生核心素養的全面發展，如數學抽象、數學建模、數學運算等.這要求教師堅持發展性原則設計教學過程，時刻關注學生核心素養的發展情況.

（三）繼承性原則

函數是高中數學課程的主要教學內容，高中數學課程卻不是函數教學的唯一支點.在初中階段，同樣重視函數教學，設置函數的概念、一次函數、二次函數、反比例函數等教學內容，為高中數學函數模塊教學奠定基礎.為此優化高中數學函數模塊教學，應堅持繼承性原則，適當對接初中函數的教學內容，激活學生的已有知識和學習經驗.

三、高中數學函數模塊的教學策略

具體在實際教學中，高中數學函數模塊的探究、發展、繼承，體現在承上啟下、生活化學習、信息化學習、問題教學、習題訓練、總結梳理、文化拓展中.據此改進教學活動，可以從高效預習、形象教學、直觀分析、深化探究、遷移實踐、強化記憶、拓展學習等方面，重塑教學流程.

（一）承上啟下，高效預習

回顧初中數學課程的函數知識，其內容如函數的概念、一次函數、二次函數、反比例函數、銳角三角函數，都為高中數學函數模塊的教學活動奠定基礎.通過初中階段的函數課程，使學生認識到函數主要研究變量之間的關系，使學生能夠借助平面直角坐標系中的描點和連線理解函數圖像與表達式的對應關系，讓更多學生具有良好的函數學習能力，進而在高中數學函數模塊的教學中，適當對接初中函數的教學內容.特別是在預習階段，教師可以直接提示學生回顧初中函數的相關知識，引導學生溫故知新，建立清晰的學習目標.

同時，教師可向學生提供微課視頻、預習單等助學資源，提高學生的預習效率.比如“函數概念與性質”的相關教學，教師可以聯系初中階段“函數的概念”，設計以下預習單，引導學生回顧之前學過的函數概念表示法、函數實例，自主預習新課內容.

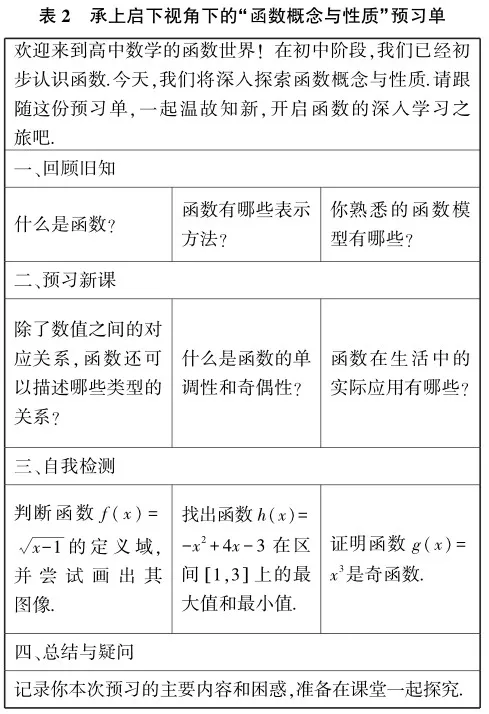
初中階段的函數概念教學相對重視直觀性和具體性，高中階段的函數概念教學則更加重視普遍性和抽象性.教師可以從具體到抽象，分析交叉知識點，設計上述預習單，輔以微課視頻促進學生的自主預習，使學生借助已有經驗，從特殊到一般，自主探索函數概念與性質的普遍性，完善課堂探究準備.

（二）銜接生活，形象教學

函數描述客觀世界的變量關系和規律，能夠解決生活實際問題.由此把握函數與生活的密切聯系，教師應當在高中數學函數模塊的教學中，積極銜接生活，落實形象教學.教師可以先收集生活資料，將函數問題與生活實例相結合，如氣溫變化、商品折扣、價格關系等，讓學生體會函數知識的實用性.緊接著，教師可通過案例分析，引導學生直觀體會函數的概念、性質、應用，建立直觀認識，降低學習難度.

比如“冪函數”的相關教學，要求學生理解冪函數的基本概念和形式，掌握冪函數的圖像特征，能用冪函數分析和描述一些現實問題.教師可以收集近幾十年的某城市人口增長數據，制作成圖表，繪制相應的函數圖像.緊接著，引導學生用數學模型描述城市的人口增長規律，討論函數的不同取值與圖像形狀和數據增長趨勢的聯系.

教師可通過生活化內容的探究，使學生自然而然地得出以上結論，深入認識冪函數，感受函數模型在解決問題中的重要作用.

（三）技術賦能，直觀分析

《新課標》指出：“重視信息技術運用，實現信息技術與數學課程的深度融合.”隨著現代科技的發展，信息技術與教育工作的融合日益緊密，為高中數學函數模塊的教學帶來便利.教師可以應用信息技術手段，進一步將高中數學函數模塊教學由抽象化為形象，以此促進學生對函數性質的直觀分析.教師也可以鼓勵學生使用信息軟件自主繪制函數圖像，豐富學習體驗.

比如“對數函數”的相關教學，考慮到其與“指數函數”相互銜接，教師可以基于學生的“指數函數”探究學習經驗，直接鼓勵學生使用GeoGebra軟件，繪制對數函數圖像，分析圖像反映的重要信息.

首先，學生在軟件的輸入框中輸入對數函數的表達式，設置繪圖區域，完成圖像繪制.其次，直觀分析圖像，學生可以明確對數函數的定義域為（0，+∞），值域為R，恒過定點（1，0），在a>1時單調遞增，在0

教師在引導學生自主繪制圖像并自主總結對數函數性質，再鼓勵學生大膽發言，交流自己的發現.在學生基本達成共識、認識對數函數的基礎上，教師可以應用信息技術手段，同步出示對數函數與指數函數圖像，使學生直觀分析其差異，避免混淆知識點.

（四）問題導學，深化探究

問題導學是引導學生深化探究學習的重要手段.通過問題導學，培養學生主動思考問題的良好習慣，提升學生的思維水平，使學生逐漸學會學習，有效深化高中數學函數模塊的探究教學.教師可以充當引導者和問題的提出者，通過一系列有層次、有梯度的問題，啟發學生深入思考函數，充實探究學習成果.

問題可以是基于生活情境的實際問題，也可以是突出學科特色的抽象問題.比如“三角函數”的相關教學，教師可以串聯新舊知識點，聯系現實生活，設置如下問題鏈：

1.擁抱自然，放松身心.假設在爬山過程中，你站在距離地面高度為10米的山腰上，手持一個與地面夾角為30°的望遠鏡觀察遠處的風景.請問視線與地面的相交點距離你有多遠？

2.回顧之前學過的直角三角形，已知一個銳角為θ，對邊長為a，鄰邊長為b，斜邊長為c，請解釋并寫出正弦函數、余弦函數、正切函數的定義式.

問題先從生活引入三角函數的概念，激發學生的思考興趣，從直觀到抽象過渡，深入追問三角函數的定義、證明等，要求學生進行更加復雜的自主思考、小組合作、集體交流等.教師通過有序推進探究，明確各項問題的答案，能夠有效培養學生的思維能力和批判思維，使學生深刻掌握三角函數的核心知識.

（五）習題訓練，遷移實踐

習題訓練即搭建綜合實踐平臺.高中數學函數模塊教學應當搭建綜合實踐平臺，使學生遷移運用學習內容，感受函數模型的實際應用價值.教師可以精選習題資源，引導學生自主解決問題，培養學生的問題解決能力.同時，教師應認識到習題訓練與題海戰術的本質區別，注重習題量的合理安排.必要時，教師可以先劃分學生層次，再根據學生的真實能力，開發分層習題.

習題涵蓋誘導公式的基本概念、三角恒等變換、三角函數的綜合應用，從簡單到復雜地訓練學生綜合實踐能力.教師可使學生回顧學習過程，自主評估綜合實踐短板，在習題中查缺補漏.

（六）整體總結，強化記憶

從整體上看，高中數學函數模塊分為四個單元，而在教學過程中，通常以更小的課時為單位.這使得學生的學習內容以碎片化方式呈現.為強化學生的知識記憶，教師可以引導學生整體總結函數知識，建立網絡化的知識框架.在構建知識框架期間，教師鼓勵學生根據個人習慣，自主選擇思維導圖、樹狀圖等，整理所學知識點的聯系和區別，同時通過回顧綜合實踐、整理錯題資源，達到整體總結學習的目的.

比如“函數應用”的相關教學，要求學生綜合運用高中數學函數模塊的相關知識，創新解決實際問題.教師可以在習題訓練的基礎上設置整體總結任務，使學生進一步回顧整體學習，建立“函數”知識框架.具體總結中，教師可以先出示優質參考，啟發學生從不同角度整理學習內容，并引導學生選擇不同的思維可視化工具，自主經歷知識的整體總結過程，建立個性化的知識框架.

此外，教師還可以設計展示與評比環節，讓學生輪流介紹自己的知識框架，分享其知識總結思路，再讓學生投票，評選最清晰的知識脈絡.整體總結與展示評比相輔相成，學生之間相互學習，持續完善知識框架，有利于強化記憶效果.

（七）滲透文化，拓展學習

數學文化包括數學的思想、語言、方法、觀點等，以及數學在人類生活、科學技術、社會發展等方面的應用.任何與數學相關的人文活動，都是數學文化的表現形式.在函數的形成和發展中，積累了豐富的數學文化.在高中數學函數模塊的教學中，教師應響應滲透數學文化，組織學習活動，開闊學生視野.教師可以成為數學文化的分享者，以講故事、設任務等形式進行拓展教學，調動學生的好奇心和求知欲.教師也可以鼓勵學生自主收集數學文化，分享發現和感悟，涵養精神世界.

再如“函數概念與性質”的相關教學，教師可向學生布置收集任務，讓學生自主收集歷史資料，調查函數的產生與發展過程，完成“函數的前世今生”調查報告.課堂教學前，教師先讓學生分享預習收獲和調查結果，再依據學生學習情況詳細講解函數的概念與性質.

相較于直接講解抽象的函數知識，以數學文化導入課堂教學，能夠進一步調動學生的求知欲，提高其探究學習熱情.同時，通過自主收集資料形成報告，能夠創新培養學生的自主學習能力，使學生認識到數學文化的重要價值，在之后的函數學習中，也能自覺收集文化資源，輔助學習課內知識.

結 語

總而言之，函數作為描述客觀世界變量關系和規律的最基本的數學語言和工具，在解決實際問題中發揮重要作用.在高中數學課程中，函數更是貫穿始終，占有關鍵地位.教師需要繼續深入探索高中數學函數模塊的教學策略，采取恰當的教學方法，完成連貫的教學活動，促使學生掌握基礎概念，也能進行綜合實踐，從而全面發展核心素養.

【參考文獻】

[1]火揚藺.基于深度學習的高中函數教學路徑探索[J].試題與研究，2023（26）：55-57.

[2]孔鑫輝.高中數學課程中的函數教學[J].中學數學教學參考，2022（27）：3-4.

[3]侯嬌.初高中數學函數教學銜接性的實踐研究[J].數學學習與研究，2021（35）：23-25.

[4]郭芳.高中數學函數設計思路及教學探討[J].新課程教學（電子版），2022（1）：122-123.

[5]翁愛蘭.有效促進深度學習的高中數學函數教學探究[J].高考，2022（14）：33-35.

[6]姜銳.高中函數單元教學目標設計與銜接策略[J].讀寫算，2021（31）：202-203.

[7]潘玉香.淺析高中數學函數教學的困境和突破[J].科幻畫報，2021（7）：125-126.