數形結合思想下的初中數學解題方法探究

【摘要】在數形結合思想下，初中數學不再局限于傳統的解題方法，以形助數、以數解形，化抽象描述為形象表達、化困難問題為簡單任務，使學生不斷創新解題方法，提高問題解決能力.教師應加強數形結合思想的滲透，使學生多實踐、巧解題.文章基于數形結合思想在初中數學解題中的優勢，從“數與代數”“圖形與幾何”兩個方面，研究數形結合思想下的初中數學解題方法，提出在絕對值、不等式、函數、三角形、面積等問題中，靈活應用數形結合思想的技巧.

【關鍵詞】初中數學；數形結合；解題方法

數和形是數學中最古老、最基本的研究對象，數形結合也是數學中最重要的思想方法之一.數和形在一定條件下發生轉化，產生一定聯系，即數形結合.以數形結合理解和解決問題，能夠有效促進復雜問題的簡單化，培養學生的數學思維和問題解決能力.在初中數學中，數形結合同樣具有優勢.利用數形結合思想解決問題，不僅能豐富解題方法，而且能進一步培養學生思維品質.教師應深入挖掘數形結合思想對初中數學解題的實際作用，幫助學生養成數形結合習慣，提高問題解決能力.

一、數形結合思想在初中數學解題中的優勢

數與形的相互轉化，一方面是借助數的精確性闡述形的某些屬性，另一方面是借助形的直觀性闡明數的某些關系.故而在數形結合思想下進行初中數學解題，能夠以形助數，亦可以數解形.

數與形的結合，強調將抽象的數學語言、數量關系與直觀的幾何圖形、位置關系聯系在一起.如此進行初中數學解題，既可使抽象的問題描述轉化為更形象的表達方式，也可使困難的問題要求轉化為更簡單的探究任務.學生也能發散思維，以更簡便的方式解決問題，創新解題方法.

（一）化抽象為形象

初中數學問題通常側重于抽象描述，以此提高解題難度，加強學生問題解決能力的培養.從審題分析到解決問題，經常有學生不能充分調動抽象思維.在數形結合思想下，將抽象的數學描述轉化為形象的圖形表達，能夠有效降低審題和分析難度，梳理解題思路.緊接著，學生精準代入已知條件，即可提高解題效率和準確率.

（二）化困難為簡單

初中數學問題的復雜性，使許多學生感到困難，不能正確解題.而在數形結合思想下，將復雜問題拆解為更直觀的表現形式，能夠化困難為簡單.通過直接觀察，學生能夠快速找到解決問題的突破口，將困難的解題過程轉化為簡單的探究任務，提高問題解決效率.

（三）化守舊為創新

數形結合思想為解決初中數學問題帶來新角度，因此在數形結合思想下，學生能夠不斷克服思維定式.除了“數與代數”“圖形與幾何”板塊的常規解題方法，學生可以多元挖掘其中隱含規律和隱藏聯系，開闊解題思路.在此基礎上創新解題方法，使學生高質量解決問題，在更深層次上發展思維品質.

二、數形結合思想下的初中數學解題方法

數形結合思想在初中數學中的廣泛應用，一般體現在“數與代數”“圖形與幾何”問題中.故而以數形結合思想豐富初中數學解題方法，應特別關注“數與代數”“圖形與幾何”兩個方面.

（一）數形結合解決“數與代數”問題

初中數學“數與代數”問題，包括“數與式”“方程與不等式”“函數”等.從最基本的絕對值問題，到不等式問題、方程問題、函數問題，都能應用數形結合思想.

1.絕對值中的數形結合

絕對值問題是最基礎的初中數學問題.在數軸上，一個數對應的點與原點的距離叫作這個數的絕對值.認識絕對值的概念以數軸為載體，而解決絕對值的問題，同樣可以應用數軸.例如北師大版教材七年級上冊習題2.3第4題：

數形結合解決絕對值問題，數軸突出數值關系，使學生準確比較大小.計算復雜的絕對值、同時比較多個有理數的大小，可以廣泛應用數軸，降低解題難度.

2.不等式中的數形結合

求解多個不等式組、判斷多個不等式的解集關系等，都可以借助數軸，實現數形結合.教材特別講解不等式解集在數軸上的表示方法，從講解不等式的解集概念到練習不等式及不等式組的求解，可以時刻滲透數形結合思想.

3.函數中的數形結合

方程是函數的基礎，函數是方程的延伸.在數量掌握和運用方程知識的基礎上，學生應深入探索函數問題，包括一次函數、反比例函數、二次函數等.函數問題的值域、最大值、最小值、增減性、對稱性等，都可以通過數形結合的方式進行分析.解決函數問題，可以多元應用數形結合思想.具體而言，針對不同的函數問題，可以繪制相應的函數圖像，直觀分析和解決問題.

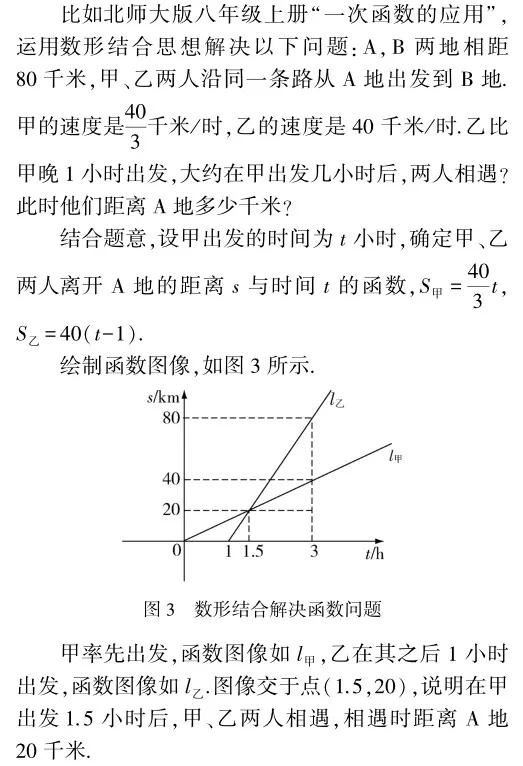
通過直觀圖像解決抽象的函數問題，使“相遇”具象化，提高解題效率.此外觀察圖像，在相遇之后，乙不斷超越甲，使學生深入思考一次函數圖像斜率的數學意義，深化一次函數的理論學習.

（二）數形結合解決“圖形與幾何”問題

初中數學“圖形與幾何”問題，包括“圖形的性質”“圖形的變化”“圖形與坐標”等.根據已知條件判斷圖形的性質，根據圖形的坐標與變化計算面積、證明性質等，也能應用數形結合思想.

1.三角形問題與數形結合

三角形作為最基礎的多邊形，在初中數學教學中占據重要地位.以北師大版初中數學教材為例，七年級下冊“認識三角形”“圖形的全等”、八年級上冊“勾股定理”、八年級下冊“三角形的證明”、九年級下冊“三角函數”等，都是三角形的核心知識.從判斷三角形的基本性質，到證明全等三角形、證明直角三角形和等腰三角形、用勾股定理和三角函數解決問題，都涉及數形結合思想.解決豐富的初中數學三角形問題，可以全面運用數形結合思想.

具體解題中，學生可以根據三角形的幾何性質進行代數計算，如正向運用勾股定理，計算直角三角形的斜邊長度，也可以通過代數方法，解決復雜的幾何問題.

第一，利用三角形的幾何性質進行代數計算.通過學習三角形的基礎知識，學生已經掌握了三角形的基本公式，如在直角三角形中，用a，b，c分別表示兩條直角邊和斜邊，a2+b2=c2.對應解決邊長問題，可以直接利用三角形的幾何性質進行代數計算.

例如：已知一個直角三角形，其直角邊長分別為8厘米和15厘米，求這個直角三角形的斜邊長.

基于圖形的基本性質，直接進行代數計算，簡化煩瑣的分析過程，提高解題效率.

第二，利用代數方法解決三角形的幾何問題.利用代數方法解決三角形的幾何問題，首先需要根據題目給出的幾何條件，建立三角形相關的代數表達式.其次，根據題目的具體要求和已經建立的代數表達式，建立代數方程或方程組.最后解方程，將代數方程的解代回原幾何問題，解釋和驗證原幾何問題的正確答案.三角形的邊長關系、角度問題、面積分析等，都可以應用代數方法進行解決，體現數形結合思想.在一些題目中，也可以直接對代數表達式進行計算.

例如：一個人由山底爬到山頂，需先爬坡角為40°的山坡300米，再爬坡角為30°的山坡100米，求山坡的實際高度.

根據題意，山坡的實際高度即山底與山頂的垂直距離，因此可以將問題轉化為一個直角三角形問題.第一個山坡坡角為40°，邊長為300米，需要求出垂直于地面的直角邊的長度.第二個山坡坡角為30°，其中斜邊長為100米，同樣需要求出垂直于地面的直角邊的長度.兩個山坡的“高度”相加，即為山坡的實際高度.建立關于兩條直角邊的代數表達式，h1=300×sin40°，h2=100×sin30°，h=h1+h2.直接計算兩個代數表達式，即能求出山坡的實際高度h.sin40°≈0.643，sin30°=0.5，h=300×0.643+100×0.5=242.9（米），則山坡的實際高度為242.9米.

通過將復雜的幾何問題轉化為簡單的代數問題，用代數方法進行靈活計算，精準解決具體問題，使學生熟練應用三角形的基礎知識.

2.面積問題與數形結合

面積問題貫穿數學學習始終.初中數學中，面積問題的難度系數進一步提高，尤其是“坐標—面積”問題.問題以平面直角坐標系為背景，給出一些具體坐標，要求學生計算相應的圖形面積.雖然根據坐標信息，能夠確定具體圖形，但是圖形邊長、高度等信息位置，使面積難以直接計算.運用數形結合思想解決問題，先從坐標切入，分析圖形的代數關系，再將具體數值代入面積公式，順利解決問題.

例如：在平面直角坐標系中，四邊形ABCD四個頂點的坐標分別為：A（1，2），B（3，4），C（5，2），D（3，0）.求四邊形ABCD的面積.

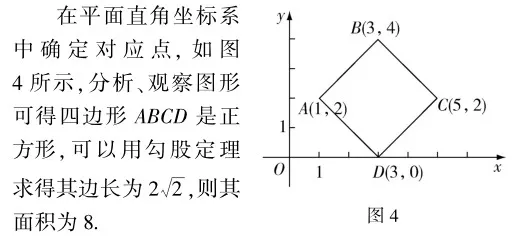
以數解形解決面積問題，準確把握數與形的對應關系，提高問題解決能力.

結 語

總而言之，在數形結合思想下，同時運用抽象思維和形象思維進行解題，能夠降低初中數學解題難度，使學生豐富解題方法，提高解題能力.解決初中數學問題，尤其是“數與代數”“圖形與幾何”問題，可以靈活運用數形結合思想.教師應加強學生的數形結合思想指導，使學生自覺化抽象為形象，化困難為簡單，創新解題方法.如此完善初中數學教學，有利于更多學生提升思維品質，達成深度學習目標.

【參考文獻】

[1]高英凱.數形結合在初中數學解題中的應用[J].數理化解題研究，2023（35）：20-22.

[2]邱春霞.以形助數以數解形“數形結合”讓初中數學化繁為簡[J].讀寫算，2023（33）：14-16.

[3]金瑜.初中數學教學中數形結合思想的滲透措施分析[J].數理天地（初中版），2023（21）：65-67.

[4]汪振宇.初中數學解題中數形結合的應用[J].中學教學參考，2023（26）：32-34.

[5]王蕓.數形結合思想在解題中的應用[J].數理天地（初中版），2023（17）：18-19.