運動約束下的分布式無人船協同編隊與導航方法

摘要：為解決集中式的無人船協同編隊與導航方法受限于控制信息開銷過大的問題，提出一種運動約束下的分布式無人船協同編隊控制與導航方法。該方法首先利用動力學模型構建了運動約束下的分布式無人船系統模型，通過局部坐標計算控制方向改變航向矢量，以允許無人船在維持特定隊形的同時向目的地移動。其次在運動速度約束條件下，構建了控制增益優化模型。最后，利用半正定松弛方法優化無人船的控制增益矩陣，以實現運動約束下的線速度和角速度的最優控制。仿真結果驗證了該方法無需無人船之間的通信，可有效實現協同編隊與導航。

關鍵詞：無人船；分布式系統；協同編隊控制；感知信息；增益優化

一、前言

無人船（Unmanned Surface Vehicle，USV）作為智慧海洋戰略中的關鍵部分，為空天地海一體化的實現提供了可靠保障[1]。無人船的智能化在很大程度上依賴于信息獲取和交換的能力[2]，隨著人工智能、大數據、云計算和物聯網等技術的融合，無人船的自主性、環境感知和決策能力得到了顯著提升[3]。因此，具有高速率、低延遲特性的編隊與導航方法在無人船集群中有廣泛應用前景。然而，由于部署的USV數量的增加，對通信阻塞現象敏感，因此集中式控制需要密集部署基站來確保通信的穩定性，導致成本和能耗顯著增加，有限的通信帶寬趨于飽和。此外，集中式控制缺乏對通信干擾、硬件故障，以及欺騙、惡意攻擊的應對方式。因此，如何以分布式擴大通信范圍并提升其穩定性成為亟待解決的問題。

多船協同編隊控制通過協調多艘不同類型的USV，旨在讓集群中的多艘USV沿著期望的編隊機動軌跡航行并保持[4]。分布式無人船集群系統允許單個USV根據其機載傳感器獲取的本地觀測結果做出決策。Sun等人[5]研究了USV編隊自主導航系統，提出的動態可調諧快速行進算法不僅可以調整規劃路徑的安全性和長度，還可以根據USV編隊和目標船只的運動信息不斷重新規劃路徑。Zhao等人[6]提出了一種分布式模型預測等高線控制方法，通過對相鄰USV之間的輪廓參數差異進行懲罰，以實現分布式編隊控制，并同時優化控制輸入，從而平衡跟蹤精度和跟蹤速度。Liu等人[7]針對復雜環境中信息不完整、局部觀測、通信約束和速度缺失的問題，利用基于神經網絡的無跡卡爾曼濾波器預測觀察到的USV的速度，實現在完成追擊和包圍任務的同時規劃無碰撞的最佳速度。

針對上述研究中的集中式無人船協同編隊與導航方法存在聯合信息獲取困難、控制信息開銷過大等問題，本文提出一種基于感知信息輔助的分布式無人船協同編隊與導航方法。本方法具體貢獻如下：

第一，構建了感知信息輔助的分布式USV協同編隊與導航場景模型，利用無人船動力學模型，將相鄰USV的姿態信息納入問題建模，并基于此構建了感知輔助的分布式無人船編隊導航的系統模型，通過改變航向矢量以允許無人船在維持特定隊形的同時向目的地移動。

第二，提出了一種基于USV感知信息的分布式控制算法。利用每艘無人船自身以及來自鄰近船只的狀態信息模型，使每艘無人船可以自行調整航向和速度，從而達到預定的編隊形狀，以避免與實際環境交互帶來的過度開銷。

第三，提出一種控制增益優化的半正定松弛迭代優化方法。該方法在最大化運動速度約束條件下，構建了控制增益優化問題模型，實現了線速度和角速度的最優化。

二、系統模型和問題描述

（一）系統模型

圖1為系統模型，考慮一個由N個無人船組成的分布式集群N=1，2，…，N，通過感知相鄰無人船之間的信息建立無人船之間的通信，從而實現編隊控制和導航策略。

對于第n∈N架無人船，動力學控制矢量表示為：

其中，?i∈Nn為第n架無人船相鄰的無人船集合，Ani∈R2×2，?n∈N，i∈Nn為控制增益矩陣，表示為：

于是，第n架無人船的全局位置坐標為qn=[xn，yn ]T ∈R2，可以得到：

對于無人船集群 N，總位置矩陣為Q=[q1Τ，q2Τ，…，qNΤ]T，總控制矩陣為u=[u1Τ，u2Τ，…，uNΤ]T，而總增益矩陣A由增益塊矩陣Ani組成，可以表示為A=[Ani]，?n∈N，i∈N。因此，具有運動約束的分布式無人船系統模型可以建模為：

其中，P為無人船總增益矩陣，表示為：

M為塊對角矩陣，表示為：

在任意時刻，每個USV沿著控制矢量的模的大小速度移動。由于增益矩陣具有塊的結構，可以看作旋轉、縮放矩陣，通過旋轉和縮放操作連接與其相鄰的USV無人船。

（二）運動模型和約束條件

如圖1所示，對于第i個無人船用戶，qi=[xi，yi]T∈R2表示無人船i的坐標，θi∈[0，2π）表示相對于全局坐標系的航向角。定義USV的單位航向矢量hi=[cosθi，cosθi]T∈R2，及其正交矢量hip，νi和ωi分別表示無人船的線速度和角速度，則無人船的運動學模型可以表示為：

可以定義H∈[h1，h2，…，hn]Τ為總航向矩陣，相對應的正交矩陣為Hp，v=[v1，v2，…，vn]Τ為線速度矢量、w=[ω1，ω2，…，ωn]Τ為角速度矢量。因此，無人船的運動模型表示為：

其中，矩陣H=diagh1，h2，…，hn，Hp=diagh1p，h2p，…，hnp。

對于任意的νmaxgt;νmingt;0和ωmaxgt;0，無人船的航速vi和航向角ωi約束條件表示為：

三、無人船分布式編隊控制

考慮尋找為無人船分配合理的ν和ω，使它們自主地實現期望的編隊并向理想的方向航行。無人船i為了確定最終形成的編隊，控制率可以進一步表示為：

其中，dij表示無人船i與j之間的距離，dij*∈R是期望值。

假設總增益矩陣 的核的一組基表示為N=[q*，qp*，1，1p]，通過SVD分解得到：

其中，U=[Qp Q]為正交矩陣，QTPQ為P的正交投影，為對稱矩陣，具有實特征值。

因此，可以建立以下優化問題：

其中，λmin表示矩陣的最小特征值。注意到，上述的優化問題是凸的，可以轉化為一個半正定規劃（SemiDefinite Programming，SDP）問題，改寫為：

可以使用CVX工具來求解，用于找到穩定增益矩陣P。

對于第i架無人船，假設pi∈R2是期望目標位置的單位常數航向矢量，在到達目的地時應沿該單位向量航行。每架無人船計算控制向量為ui+cpi，cgt;0是一個恒定的期望速度。然后計算該矢量沿航向hi及其垂直矢量hip的投影，并分別作為線速度和角速度。線性和角速度控制由以下控制給出：

假設pi對所有無人船都是相同且為常數。

進一步考慮無人船的運動約束，根據上述給定的運動學航速和航向角的約束控制，對于USV的速度νmin≤νi≤νmax，線速度可以表示為：

而對于|ωi|≤ωmax，角速度表示為：

則在該控制下，無人船將以期望的速度向目的地移動時收斂到所需的編隊。

四、仿真結果與分析

為了驗證本文提出方法的有效性，本節對動力學約束下的分布式無人船協同編隊控制與導航方法進行了仿真。期望的編隊形式被定義為三角形，所有無人船的期望行進方向為沿著全局坐標系的正x軸，即pi=[1，0]T。航向角變化率最大為π/4。對于每個編隊，考慮控制律（15）和（16），其中ui由（10）給出。

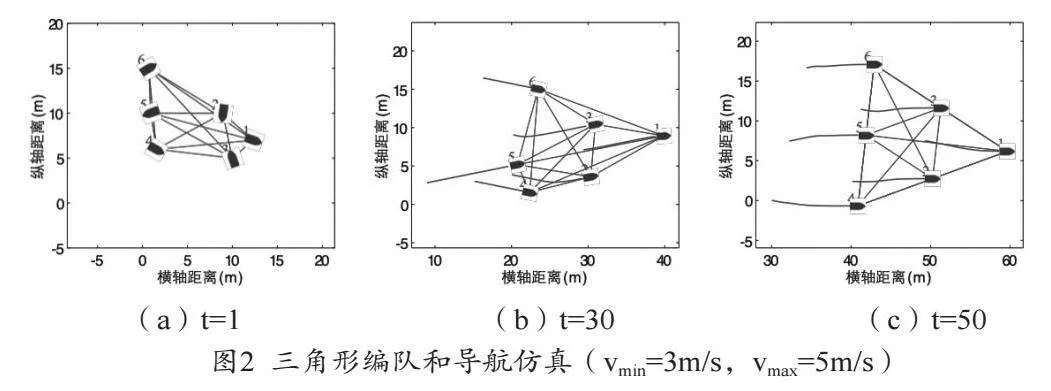
圖2為運動約束下的分布式無人船協同編隊控制與導航結果，探究了三角形無人船編隊隨時間變化情況的影響，采用增強控制率來確定三角形的編隊形式。假設無人船初始位置和航向矢量是隨機的，共有6架無人船構成群組，無人船的運動約束最小速度和最大速度分別設置為3m/s和5m/s，無人船與其相鄰無人船之間的期望距離定義為d=10m。由圖2可知，所研究的控制策略將無人船導航到期望的三角形編隊形式，并以理想的編隊形式航行。編隊控制只使用局部相對位置預測，通過旋轉和平移才能達到所需的編隊。當t=30標準間隔時，隊形逐漸收斂于期望形狀。由于此時在增強控制率的約束下，無人船期望編隊的形成方向是固定的，不會受到初始狀態的影響，無人船之間的距離達到期望值10m。

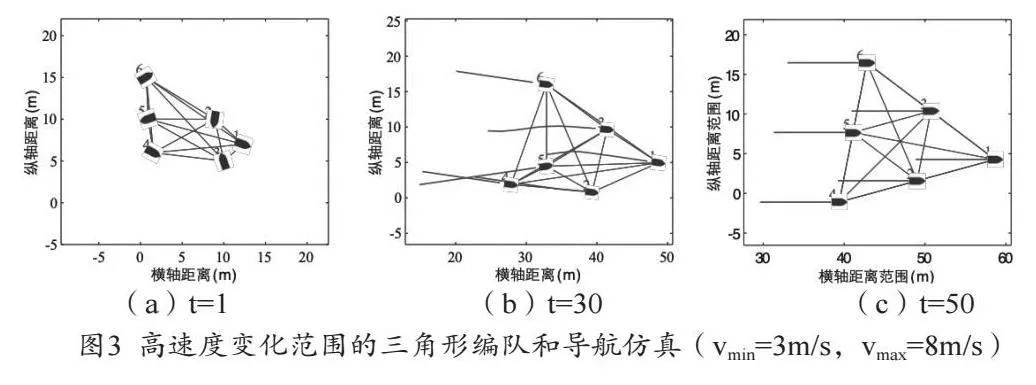
圖3為高速度變化范圍分布式無人船協同編隊控制與導航結果，最小速度和最大速度分別設置為3m/s和8m/s。所研究的控制策略同樣可以將無人船導航到期望的三角形編隊形式，并以理想的編隊形式航行。通過對比不同速度范圍的編隊和導航情況可知，速度的變化范圍越小，集群開始收斂的速度越慢，但最后達到收斂的速度越快，算法越容易達到期望的效果。而速度的可變化范圍越大，可調節的范圍越寬，雖然形成初步形狀的速度越快，但是達到收斂所需的時間也會隨之略微增加。原因在于無人船的速度越接近，形成期望隊形的最優速度更快，因此適當的運動約束才能有助于提高預測精度，進而提高協同編隊和導航的性能。然而，速度范圍過高會包含冗余的運動態勢信息，從而導致性能下降。

本文提出的運動約束下的分布式無人船協同編隊與導航方法，通過奇異值分解從信道中獲得增益矩陣，并選取最小的矩陣特征值，以局部坐標替代了全局坐標，不需要與真實環境交互進行信道探測，在降低信道探測開銷的同時，有效地提高了無人船通信和導航效率。

五、結語

本文研究了運動約束下的分布式無人船協同編隊與導航方法。針對由集中式控制等引起的高控制開銷問題，采用了分布式控制技術以獲取相鄰無人船的目標位置和導航運動矢量信息。為解決與控制中心交互進行數據傳輸所帶來的大量開銷問題，提出了基于運動約束的分布式無人船控制和導航控制增益優化模型，并利用局部坐標信息替代全局坐標信息。給定一個理想的編隊情況，結合SDP，提出優化算法以獲得穩定的無人船控制增益，用于計算運動約束下的線速度和角速度。通過仿真結果驗證了本文提出的分布式無人船控制和導航方法的有效性，并且該模型降低了通信和控制的開銷，從而提高了該方法在無人船場景中的可行性。

參考文獻

[1]Wang J B， Zeng C， Ding C， et al. Unmanned surface vessel assisted maritime wireless communication toward 6G： opportunities and challenges[J]. IEEE Wireless Communications， 2022， 29（06）： 72-79.

[2]Zeng H， Su Z， Xu Q， et al. Game Theoretical Incentive for USV Fleet-Assisted Data Sharing in Maritime Communication Networks[J]. IEEE Transactions on Network Science and Engineering， 2024， 11（02）： 1398-1412.

[3]Liao Y， Song Y， Xia S， et al. Low-Latency Data Computation of Inland Waterway USVs for RIS-Assisted UAV MEC Network[J]. IEEE Internet of Things Journal， 2024， 11（16）： 26713-26726.

[4]Xue K， Ren C， Ji X， et al. Design， Modeling and Implementation of a Projectile-Based Mechanism for USVs Charging Tasks[J]. IEEE Robotics and Automation Letters， 2023， 8（01）： 288-295.

[5]Sun X， Wang G， Fan Y， et al. A formation autonomous navigation system for unmanned surface vehicles with distributed control strategy[J]. IEEE Transactions on Intelligent Transportation Systems， 2021， 22（05）： 2834-2845.

[6]Zhao M， Li H. Distributed model predictive contouring control of unmanned surface vessels[J]. IEEE Transactions on Industrial Electronics， 2024， 71（10）： 13012-13019.

[7]Liu Y， Liu C， Meng Y， et al. Velocity domain-based distributed pursuit- encirclement control for multi-USVs with incomplete information[J]. IEEE Transactions on Intelligent Vehicles， 2024， 9（02）： 3246-3257.

基金項目：江蘇科技大學博士啟動基金“基于統一互信息的雷達通信一體化系統優化研究”（項目編號：1132932104）

作者單位：羅浩、賴卓昀，江蘇科技大學海洋學院；羅浩，河海大學信息科學與工程學院、江蘇贊奇科技股份有限公司

責任編輯：張津平、尚丹