劉震宇,王驥猛

(廣東工業大學信息工程學院,廣州 510006)

?

一種改進的基于定向天線的移動傳感器網絡定位算法*

劉震宇*,王驥猛

(廣東工業大學信息工程學院,廣州 510006)

針對在無線傳感器網絡定位中,由于全向天線信號受環境影響而造成定位誤差較大的問題,提出了一種改進的基于定向天線的移動無線傳感器網絡定位算法(DADLP),使用一個帶有定向天線的移動錨節點廣播位置信息,未知節點接收到信號后,將接收功率平均分為若干等級,縮小定位估計區域。仿真結果表明DADLP算法相對于Ssu、BLI、GGDI和RROI移動錨節點算法提高了定位精度,并且在非規則環境下有更低的平均定位誤差。

無線傳感器網絡;定位;功率分級;移動錨節點;定向天線

無線傳感器網絡WSN(Wireless Sensor Network)由大量的無線傳感器節點組成,是當前備受關注的前沿熱點研究領域,廣泛應用于環境、軍事、生產安全等領域[1]。傳感器節點的定位技術是無線傳感器網絡的關鍵技術之一,對于傳感器網絡來說,事件發生的位置是傳感器節點監測信息中的重要組成部分,離開了位置信息節點采集的數據毫無意義。

目前,無線傳感器網絡定位算法可以分為兩類:基于測距(Range-based)的定位算法和非測距(Rang-free)的定位算法。基于測距的定位算法需要獲取傳感器節點間的距離或角度信息,定位精度高,成本高。非測距的定位算法不需要直接測量傳感器節點間的距離信息或角度信息,定位精度相對低,對硬件要求低,低功耗,成本低。出于對節點的功耗、傳感器網絡成本等因素的考慮,和大多數引用場合對傳感器節點定位精度要求不高,所以非測距定位更適合大規模網絡以及未來發展[2]。

近年來,有大量文獻在無線傳感器網絡中使用移動錨節點的定位算法[3-4],傳感器網絡定位模塊使用天線可以分為兩類:定向天線和全向天線。文獻[5]中Ssu’s算法是一種經典定位算法。Ssu提出了一種使用錨節點基于幾何平分線的定位算法,此算法只需要較少的通信損耗,并且具有較高的定位精度。但是,環境因素對此算法的影響較大。

文獻[6]提出了一種使用兩個移動錨節點的定位算法,一個作為主定位節點另一個作為輔助節點來完成定位。但是,由于錨節點發送信息會有間隔,所以未知節點接收到的定位錨節點和輔助節點定位信息時的兩節點坐標會與它們的理想坐標超前,從而導致未知節點定位后的估計坐標在水平方向上存在誤差。在文獻[7]中提出了一種基于RSSI的移動錨節點定位算法。但是,此算法錨節點的移動模型為隨機軌道模型,無法確保錨節點移動過程中經過同一未知節點多次,造成部分未知節點無法完成定位。

文獻[5-7]中提出的定位算法使用全向天線來發射信號,但是,全向天線的射頻信號范圍大,容易受到外界環境因素的影響,許多算法使用定向天線來定位節點[8-9]。

文獻[9]Zhang Baoli提出了3種只使用一個定向天線來定位未知節點的算法BLI、GGDI和RROI。GGDI算法使用定向天線最大增益方向的交點作為未知節點的估計位置,RROI算法使用定向天線的相交區域來求解未知節點坐標,BLI算法雖然是利用相交區域最小的兩個移動錨節點坐標估計位置,但是誤差較大,誤差在30%～40%之間。

眾所周知,全向天線的輻射能量范圍是360°,這更容易被環境所影響,從而導致更大的定位誤差。相比之下,定向天線集中能量在一個較窄的范圍內,并且具有更高的增益,通過使用定向天線,一個傳感器節點可以有選擇的接收只從某些預期方向上的信號,從而避免大部分方向上的環境噪聲干擾,達到提高定位精度的目的。如上述研究中,Ssu提出的定位算法中傳感器節點使用全向天線來接收信號,而Zhang Baoli提出定位算法中都是使用定向天線來完成定位。Ssu所提出算法的定位誤差在40%～65%之間,遠大于Zhang所提出的定位算法。

雖然使用定向天線在一定程度上能夠避免環境帶來的額外誤差,但是現實中的定線天線主瓣寬度在60°～120°之間,定向天線的定位相交區域較大。為了減少環境因素對定位的影響,本文提出了一種使用定線天線的定位算法,并且為了進一步縮小定位相交區域,引入了功率分級的思想,以提高定位精度,并進行了軟件仿真實驗和真實試驗以驗證該算法的定位精度。

1 問題分析

1.1 Ssu’s算法原理

Ssu’s算法原理:一條弦的垂直平分線會經過這條弦所在圓的圓心。當一個圓上有兩條弦時,這兩條弦的垂直平分線的交點就是圓心。Ssu把傳感器節點的通信范圍當作是一個圓,圓上的兩條弦是錨節點移動路徑,弦的兩個端點分別為:第1次和未知節點通信的錨節點位置Nin;最后一次和未知節點通信的錨節點位置Nout。兩條弦的垂直平分線的交點即為未知節點的估計位置。如圖1(a)所示,

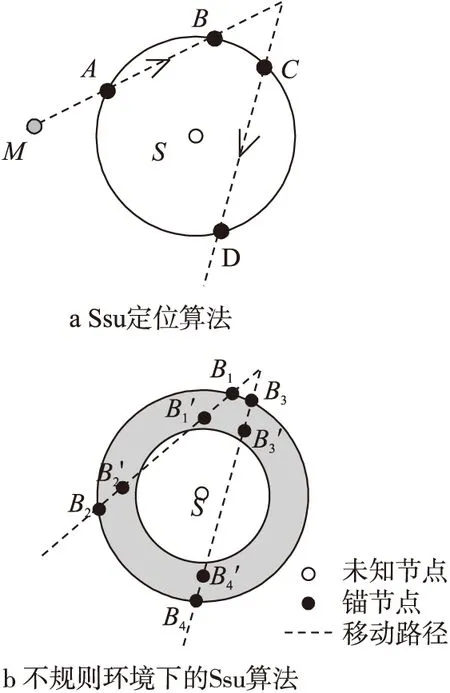
圖1 Ssu定位算法

移動錨節點M周期性發射位置信息,在其移動過程中未知節點S在其通信圓內接收到錨節點的信息,端點A、B、C和D為錨節點進入和離開未知節點S的通信范圍時的錨節點位置。弦AB和弦CD的垂直平分線交點即為節點S的估計坐標。

1.2 Ssu’s算法誤差

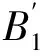
1.3 BLI算法原理

為了減少環境對定位誤差的影響,BLI算法采用定向天線進行定位。定向天線能夠集中能量在特定的方向上,并且可以縮小射頻信號覆蓋范圍。錨節點在傳感器網絡中移動,并且周期性發送位置信息,當未知節點接收到第1次通信的錨節點Nin和最后一次通信的錨節點Nout信息時,BLI算法將兩錨節點坐標的定向天線輻射邊界線的交點作為未知節點的估計坐標。

1.4BLI算法誤差

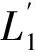
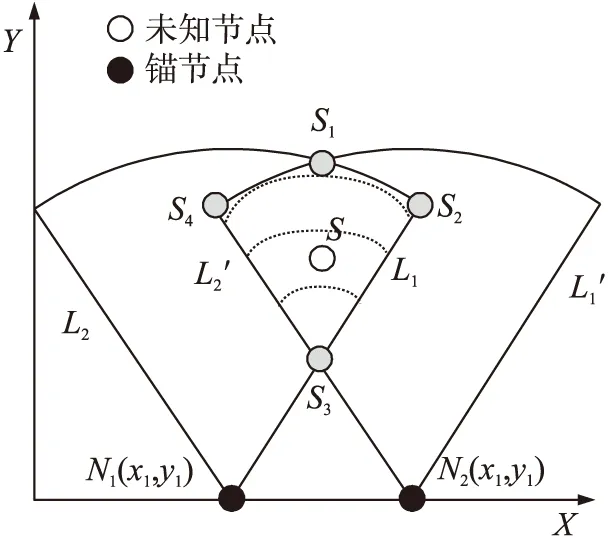
圖2 BLI算法

GGDI算法、RROI算法與BLI算法的定位精度相差±5%左右。GGDI算法使用的是定向天線最大增益交點,但是只有一部分未知節點能夠接收到最大增益信號,所以受錨節點發送信號間隔影響較大。RROI算法使用Nin和另外一個錨節點坐標(Ni),但是Ni的選擇沒有一個固定的條件,所以并不能保證Nin和Ni的相交區域最小,RROI的誤差相對BLI高5%。

2 DADLP算法

Zhang在BLI方法中采用Nin和Nout作為定位錨節點,與RROI算法相比縮小了相交區域,在一定程度上提高了定位精度。但是,假如能夠進一步縮小相交區域,定位精度將會有所提高。例如,在圖2中BLI算法所確定相交區域為S1、S2、S3、S4所組成的區域,未知節點S在相交區域的任意位置,假如能夠將相交區域劃分區域,如圖2中S1、S2、S3、S4所組成的區域以虛線弧劃分出多個區域,并且確定S屬于某一區域,這樣就可以縮小S可能存在的區域范圍,減小定位誤差。

為了進一步縮小定位區域,提高定位精度,本文引入功率分級的思想,提出了一種基于定向天線分級的移動無線傳感器定位算法(DADLP),將定向天線按照未知節點接收功率平均分級,選取適當的定位錨節點確定未知節點的坐標。

2.1 接收功率分級

首先,錨節點以固定時間間隔發射信號,未知節點接收到的功率會隨著距離的增加而減小,未知節點根據接收到的功率來判斷處于某一級處。如圖3所示,βm為定向天線夾角,L1與L2為定向天線的輻射邊界線,k1和k2為L1、L2的斜率,θ為天線邊界與水平線夾角θ=π/2-βm/2,Ni為錨節點移動到第i個位置時的錨節點坐標。定向天線輻射邊界線計算公式:

(1)

式中:k1=tan(θ),k2=-k1。例如,未知節點處于第k和k+1等級之間,令節點接收功率為Pr,未知節點到錨節點距離為d則有:

(2)

式中:Pk+1、Pk分別為k等級處最小和最大接收功率,Rk、Rk+1分別為k等級處最小和最大邊界半徑。

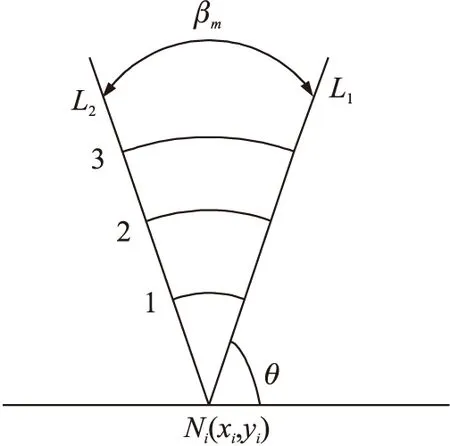
圖3 接收功率分級

但是在現實環境中,由于多徑、陰影等因素的影響,信號的傳輸范圍通常是不規則的[11],它的不規則性可以用不規則度DOI(DegreeOfIrregular)來說明。若DOI=0,則信號傳播范圍是一個規則形狀,當DOI=0.1,信號的傳輸距離在[0.9R,1.1R]范圍內變化,DOI模型下信號的接收強度表達式:

PR(d)=PT-PL(d0)-10ηlog10(d/d0)ki

(3)

式中:PR(d)為接收信號功率,PT為發送信號功率,PL(d0)為參考距離d0的路徑損耗功率,η為路徑損耗指數,d為發送端和接收端的距離,ki為不同傳播方向上的路徑損耗協同系數,ki計算公式:

(4)

式中:rand是均勻產生位于[0,1]上的數值的隨機函數。

2.2 錨節點選取

錨節點在移動過程中會形成許多虛擬錨節點,這些虛擬錨節點中有些能夠和同一未知節點進行通信。根據幾何定理:當兩個圓的圓心相距最遠時,兩個圓的相交區域最小。因此當兩個虛擬錨節點相距最遠時相交區域最小。如圖4所示,在錨節點移動期間能夠和未知節點S通信的錨節點位置有若干個,由圖4可以看出NDF和NDL的相交區域最小。

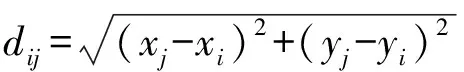
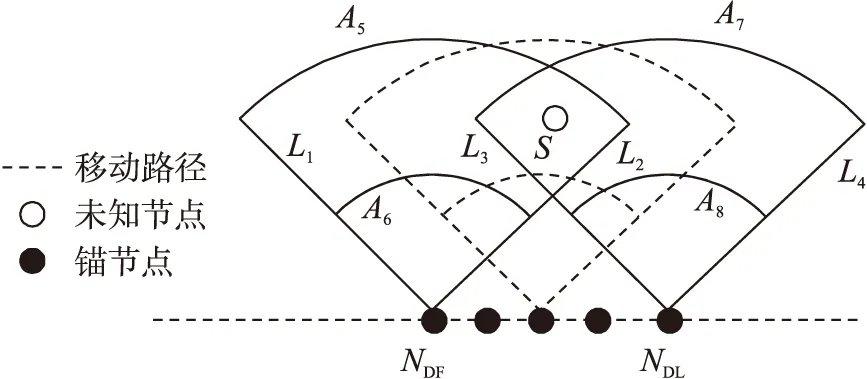
圖4 定向天線相交區域

2.3 定位區域分析和位置估計

未知節點根據接收功率的大小,確定其所在等級n,并且選取NDF(x1,y1)和NDL(x2,y2)定位錨節點,如圖4中NDF和NDL兩錨節點輻射邊界線有如下幾條:

L1:y-y1=k1(x-x1)

(5)

L2:y-y1=k2(x-x1)

(6)

L3:y-y2=k1(x-x2)

(7)

L4:y-y2=k2(x-x2)

(8)

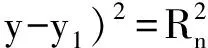
(9)

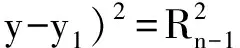
(10)

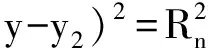
(11)

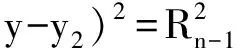
(12)

式中:L1、L2、L3、L4分別為NDF和NDL定向天線的兩輻射邊界線,k1、k2、k3、k4分別為定向天線輻射邊界線在NDF和NDL處的斜率,A5、A6、A7、A8分別為NDF和NDL在分別在等級為n和n-1的邊界弧,并且A5和A6邊界弧上點的斜率k應在k1與k2之間,A7和A8邊界弧上點的斜率k′在k3與k4之間。取邊界線相交區域的質心作為節點的估計位置。質心計算公式如下:

(13)

式中:m為相交區域頂點個數。

2.4 復雜度分析

DADLP算法在計算未知節點估計位置的計算開銷共有3種:①直線與直線相交O(1);②直線與圓相交O(2);③圓與圓相交O(3)。其中O(1)需要乘法、加法、減法各2次,O(2)需要10次乘法,加法和減法各4次,O(3)需要18次乘法,加法和減法各6次。由定位區域可知,計算未知節點的估計位置存在兩種情況:1,處于一個直線與直線交點,兩個直線與圓交點和一個圓與圓交點所組成區域;2,處于兩個圓與圓交點和4個直線與圓交點所組成區域;則有未知節點計算開銷公式如下:

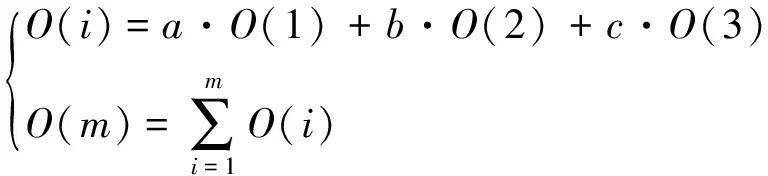
(14)

O(m)為總的計算開銷,未知節點i處于n級,N為接收功率分級,θ為定向天線邊界線與水平方向夾角,定位錨節點Nin和Nout距離為d。假如d>d0,則a=1、b=2、c=1。否則,a=0、b=4、c=2。d0計算公式如下:

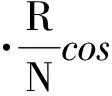
(15)

3 仿真及試驗

3.1 仿真實驗環境

錨節點的移動有許多模型[12-13]如:隨機方向模型、隨機路徑模型,短距離移動模型等。在文獻[9]中BLI算法采用短距離移動路徑模型如圖5(a)所示。但是,錨節點移動路徑在未知節點通信圓上形成的弦都是平行的,Ssu算法是使用兩條弦的垂直平分線的交點作為估計坐標的,定位所用的兩條弦平行可能會造成弦的交點不存在,許多未知節點不能完成定位,造成定位誤差偏大,比較結果有失公平。

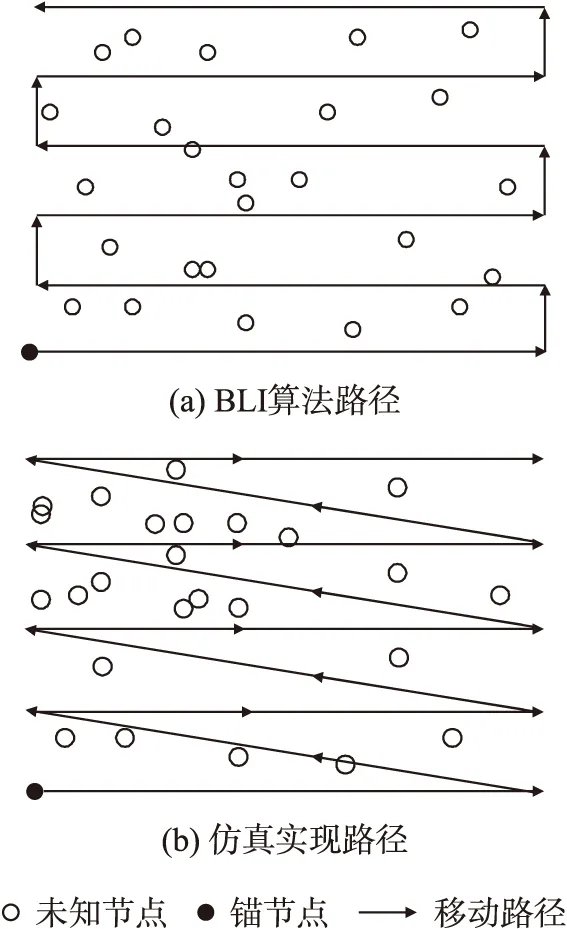
圖5 移動路徑

為了盡量減小弦平行所帶來的誤差,DADLP算法、Ssu算法、BLI算法、GGDI算法和RROI算法都采用如圖5(b)所示移動路徑。Ssu算法選取不平行的兩條弦,如圖5(b)中一條水平的弦和一條斜方向的弦來定位未知節點。這樣,DADLP、GGDI、RROI和BLI算法不受路線影響,并且Ssu算法不會因為路線造成額外的誤差。

為了驗證所提出算法的性能,采用MATLAB為仿真平臺進行試驗,并選取100×100 m2的二維平面區域作為無線傳感器網絡定位區域,100個未知節點隨機分布在傳感網絡中,節點通信半徑R,節點通信模型使用DOI模型,使用單個裝備有定向天線的移動錨節點按照移動路徑移動,錨節點發送信號時間間隔為t,n為定向天線功率級數。定位精度用平均定位誤差er來衡量:

(16)

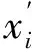
3.2 不同等級下定位誤差

在規則模型下,錨節點以固定速度移動,信號發送間隔t=0.1/s環境下,當n在[2,16]之間時,R=10 m、15 m、20 m、25 m時定位誤差如圖6所示。從圖6可以看出隨著定向天線功率等級增大,定位誤差呈下降趨勢。隨著通信半徑的增大,定位誤差呈明顯增大趨勢。這是因為當通信半徑相同時,等級越大定向天線每一級所占的環形區域就越小,因此NDF和NDL坐標處的定向天線的相交區域就越小。同樣,在等級相同時,半徑較小所以相交區域也較小,因此取相交區域的質心就越接近未知節點的真實坐標。

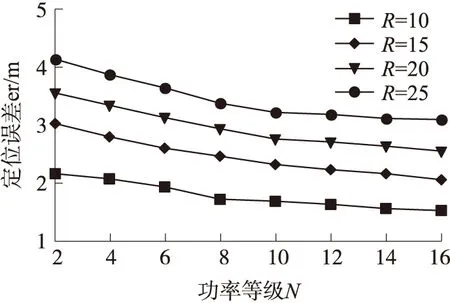
圖6 不同功率等級下的定位誤差

3.3 不同時間間隔下定位誤差

DADLP與其他4種算法在錨節點以相同固定速度下移動,DOI=0,信號發送間隔t在[0,1]之間的誤差比較。如圖7所示,DADLP算法與其他4種算法相比定位精度高。Ssu的算法的定位誤差受發送信號間隔影響較大,這是由于噪聲環境中錨節點的發送信號間隔時間越長所產生的虛擬錨節點越少,所以Nin和Nout坐標與理論上確定弦的兩個端點位置誤差較大。未知節點能夠接收到定向天線最大增益處信號的只有一部分,所以GGDI算法定位精度有限。RROI算法定向天線的相交區域較大,所以定位誤差大。BLI算法使用定向天線的交點作為未知節點估計位置,使用一個輻射邊界線交點來代替整個相交區域,誤差在30%～40%。

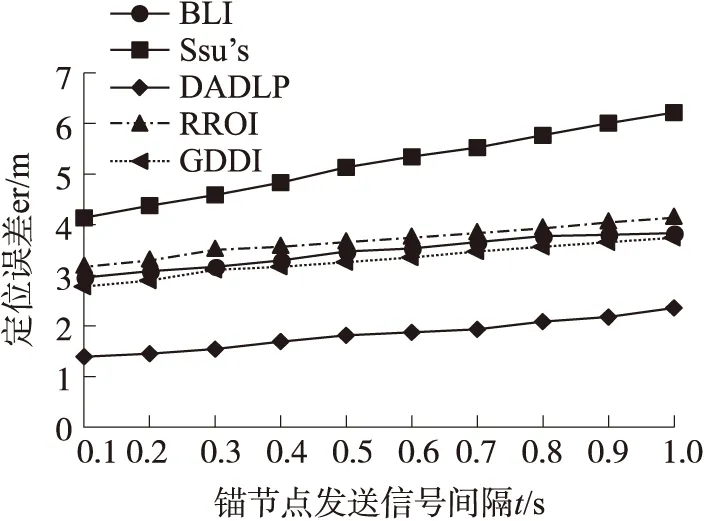
圖7 不同發射間隔下定位誤差

3.4 不同DOI下定位誤差

由于多徑噪聲等的影響,不規則度通常是變化的。如圖8所示是5種算法分別在不同DOI環境下對定位誤差的影響。由圖8可知隨著DOI的值的增大,5種算法的定位誤差都在一定程度上增大,DADLP算法定位誤差遠小于其他幾種算法,定位誤差相差至少1.1 m。

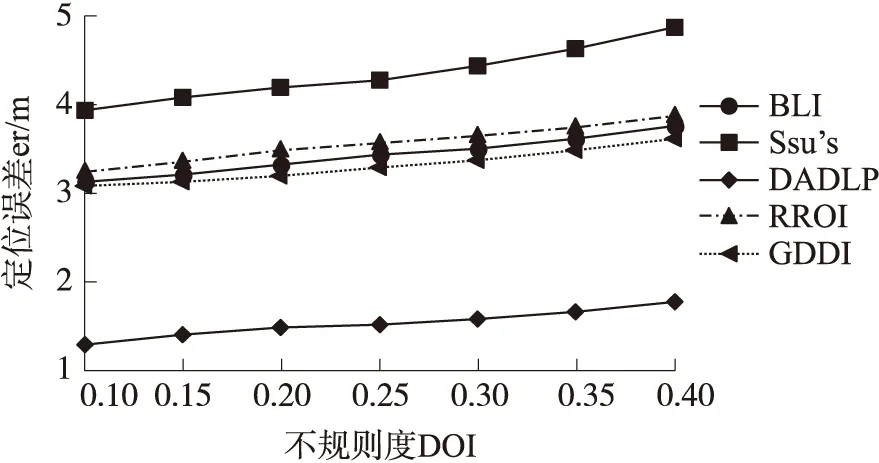
圖8 不同DOI下的定位誤差

3.5 模擬試驗

為了驗證DADLP算法在現實環境中的性能,現對其進行試驗以評估DADLP定位算法性能。由于DADLP算法采用的是移動錨節點是裝備在機器人身上的,所以試驗采用ESP8266WIFI模塊,發射功率采用802.11b模式下16 dBm的輸出功率,如圖9所示兩個WIFI模塊相隔10 m放在地面上,WIFI模塊1固定發射信號WIFI模塊2接收信號,試驗20次后得到不同距離下的平均接收功率如表1所示。

圖9 真實試驗

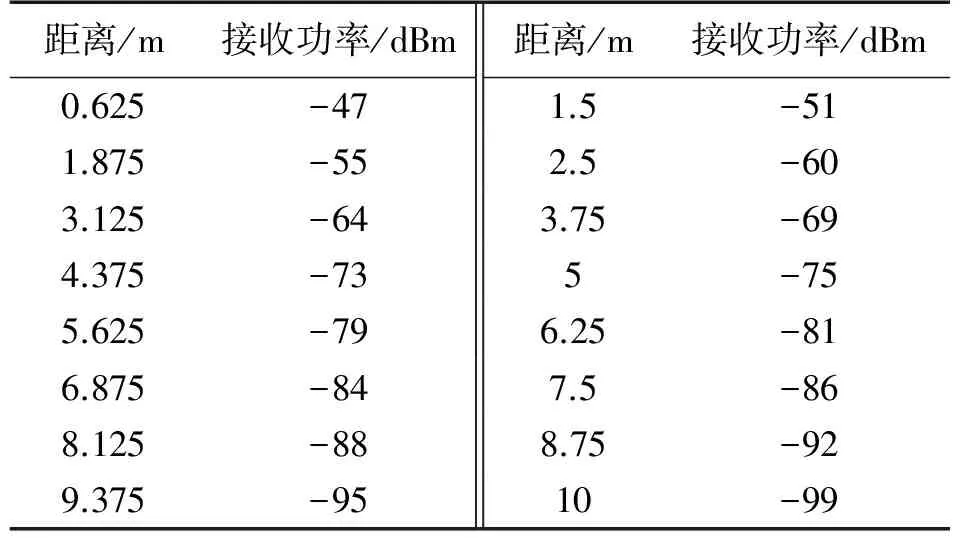
距離/m接收功率/dBm距離/m接收功率/dBm0．625-471．5-511．875-552．5-603．125-643．75-694．375-735-755．625-796．25-816．875-847．5-868．125-888．75-929．375-9510-99

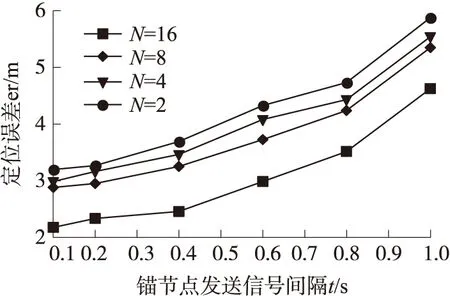
圖10 不同發射間隔下的定位誤差

算法試驗分為兩個階段,第1階段是接收功率的采集階段,未知節點周期性地采集接收功率。第2階段是利用DADLP定位算法對未知節點進行定位。試驗在通信半徑為10 m,不同信號發送間隔t下的定位誤差如圖10所示。不同半徑下的定位誤差如圖11所示。隨著半徑的增大在相同功率等級下DADLP算法定位誤差逐漸減小,并且在相同等級下半徑越小,定位精度越高,試驗結果與理論分析結果相符。

圖11 不同半徑下的定位誤差

4 結論

DADLP算法使用一個移動錨節點周期性發射定位信息,將接受功率分級,根據未知節點接收功率確定其所處等級,進一步縮小定位錨節點的相交區域,從而確定未知節點坐標。DADLP算法與Ssu的算法、GGDI算法、RROI算法和BLI算法進行比較,仿真結果表明在規則和非規則模型下,定位誤差都低于其他幾種算法,DADLP算法具有更好的定位效果。

[1] 彭宇,王丹.無線傳感器網絡定位技術綜述[J]. 電子測量與儀器學報,2011,25(5):389-399.

[2] 范時平,羅丹,劉艷林.基于跳距與改進粒子群算法的DV-Hop定位算法[J]. 傳感技術學報,2016,29(9):1410-1415.

[3] Ou C H,He W L. Path Planning Algorithm for Mobile Anchor-Based Localization in Wireless Sensor Networks[J]. IEEE Sensors Journal,2013,13(2):466-475.

[4] Abdi F,Haghighat A T. A Hybrid RSSI Based Localization Algorithm for WSN Using a Mobile Anchor Node[C]//Computing Communication and Networking Technologies(ICCCNT). International Conference on IEEE,2014:1-6.

[5] Ssu K F,Ou C H,Jiau H C. Localization with Mobile Anchor Points in Wireless Sensor Networks[J]. IEEE Transactions on Vehicular Technology,2005,54(3):1187-1197.

[6] Shi Z,Zhu Y,Shi J,et al. A Localization Scheme with Dual Mobile Beacons in Wireless Sensor Networks[J]. Information Technology Journal,2013,12(12):2426-2432.

[7] Fan C W,Wu Y H,Chen W M. RSSI-Based Localization for Wireless Sensor Networks with a Mobile Beacon[C]//Sensors,2012 IEEE.IEEE,2012:1-4.

[8] Wu Y H,Chen W M. Localization of Wireless Sensor Networks Using a Moving Beacon with a Direction Antenna[C]//High Performance Computing and Communications,11th International Conference on. IEEE,2009:237-242.

[9] Zhang B,Yu F. LSWD:Localization Scheme for Wireless Sensor Networks Using Directional Antenna[J]. IEEE Transactions on Consumer Electronics,2010,56(4):2208-2216.

[10] Zhang B,Yu F,Zhang Z. An Improved Localization Algorithm for Wireless Sensor Network Using a Mobile Anchor Node[C]//Information Processing Asia-Pacific Conference on. IEEE,2009:485-488.

[11] 王承林. 基于邊界盒節點定位算法的研究[D]. 東北大學,2012.

[12] Rezazadeh J,Moradi M,Ismail A S,et al. Superior Path Planning Mechanism for Mobile Beacon-Assisted Localization in Wireless Sensor Networks[J]. IEEE Sensors Journal,2014,14(9):3052-3064.

[13] Han G,Chao J,Zhang C,et al. The Impacts of Mobility Models on DV-Hop Based Localization in Mobile Wireless Sensor Networks[J]. Journal of Network and Computer Applications,2014,42:70-79.

劉震宇(1976-),男,博士,廣東工業大學副研究員.研究領域數字信號處理、物聯網技術和通信網安全處理,zhenyuliu@gdut.edu.cn;

王驥猛(1990-),男,碩士研究生.研究方向為無線傳感器網絡定位,a19880830@qq.com。

An Improved Localization Algorithm for Mobile Sensor Network Using Directional Antenna*

LIUZhenyu*,WANGJimeng

(School of Information Engineering,Guangdong University of Technology,Guangzhou 510006,China)

To solve the signal from an omni-directional antenna of mobile wireless sensor networks is affected by environment noise caused a big localization error problem,an improved localization algorithm(DADLP)using a mobile anchor node equipped with a direction antenna was proposed. The received power of sensor node is divided into several levels to reduce the estimated area and improve the localization accuracy. The simulation results show that DADLP has higher accuracy and lower average localization error than Ssu’s algorithm,BLI algorithm,GGDI algorithm and RROI algorithm in irregular environment.

wireless sensor networks;localization;different level of power;mobile anchor node;direction antenna

項目來源:國家自然科學基金項目(61401106);廣州市科技計劃項目科學研究專項(2014J4100206)

2016-07-17 修改日期:2016-11-21

TP393

A

1004-1699(2017)03-0456-07

C:7230

10.3969/j.issn.1004-1699.2017.03.020