關于四色猜想

沉潛

中圖分類號：O157.5 文獻標識碼：A 文章編號：1009-914X（2016）02-0374-01

證明：

【一】：在一個平面上最多只能有四個平面區域兩兩相鄰。

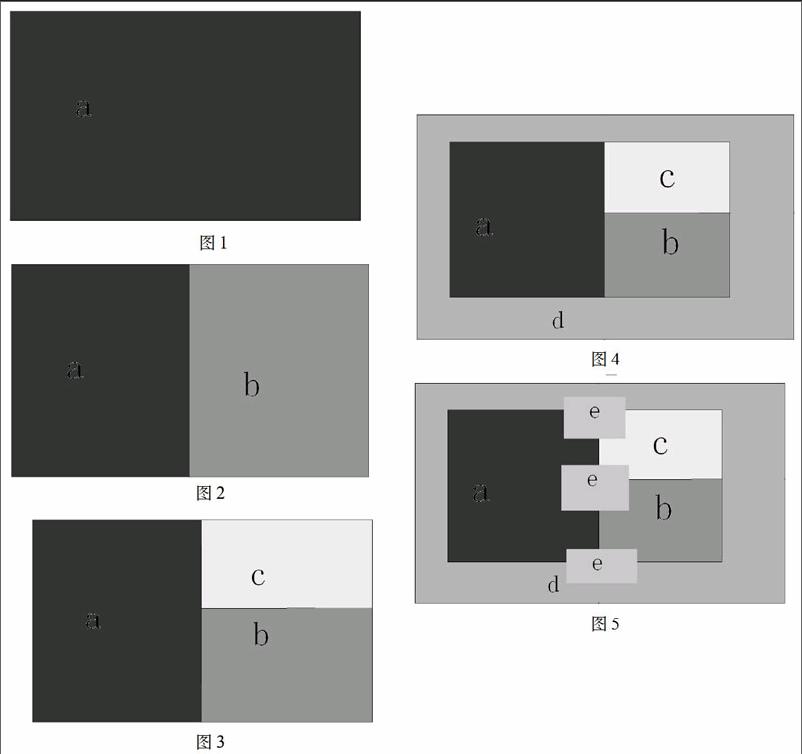
①在一個無限的連續的平面上，用一條直線將平面分割為兩個區域，分別記為區域a、區域b。此時兩個區域公共部分為一條直線。（見圖1、圖2）

②再用一條直線將兩區域公共直線分割，直線同一側的區域a區域b合為同一個區域c。此時三個區域公共部分為一個點。（見圖3）

③由于點無法繼續分割，要使第四個區域d與前三個區域都相鄰，則需要第四個區域d將原三個區域包圍。（見圖4）

④此時四個區域已無公共部分，接下來要使第五個區域e 與前四個區域都相鄰。先使區域e與三個區域相鄰。而區域e無論與哪三個區域相鄰，要與第四個區域銜接時都會被那三個區域阻擋。（見圖5）

也就是說，在一個平面上最多只能有四個平面兩兩相鄰，即四色猜想。

【二】：在一個空間上最多只能有五個立體區域兩兩相鄰。

（個人能力有限，圖略）

①在一個無限的連續的空間上，用一個無限平面將平面分割為兩個區域，分別記為區域a、區域b。此時兩個區域公共部分為一個平面。

②再用一個平面將兩區域公共平面分割，平面同一側的區域a區域b合為同一個區域c。此時三個區域公共部分為一條直線。

③繼續用一個平面將三個區域公共直線分割，平面同一側的區域a區域b區域c合為同一個區域d。此時四個區域公共部分為一個點。

③由于點無法繼續分割，要使第五個區域e與前四個區域都相鄰，則需要第五個區域e將原四個區域包圍。

④此時五個區域已無公共部分，接下來要使第六個區域f與前五個區域都相鄰。先使區域f與四個區域相鄰。而區域e無論與哪四個區域相鄰，要與第五個區域銜接時都會被那四個區域阻擋。

也就是說，在一個空間上最多只能有五個立體區域兩兩相鄰。