復雜環境下的UWB/PDR緊組合定位方法
代曉霽,李 敏,徐天河,江 楠,許 艷
復雜環境下的UWB/PDR緊組合定位方法
代曉霽1,李 敏2,徐天河2,江 楠2,許 艷2
(1. 長安大學地質工程與測繪學院,西安 710054;2. 山東大學空間科學研究院,山東威海 264209)
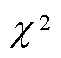
室內定位;超寬帶;行人航位推算;緊組合;復雜環境
0 引言
隨著定位導航服務的不斷發展和新技術在定位導航領域的廣泛使用[1],室內定位導航技術受到了人們極大的關注。眾多學者開展了室內定位相關的研究工作,研究成果包括藍牙[2]、無線保真(wireless fidelity, WiFi)[3]、第5代移動技術(the fifth generation of mobile technologies, 5G)[4]、超寬帶(ultra wide band, UWB)[5]、慣性導航[6](inertial navigation system, INS)、視覺定位[7]、音頻定位[8]、地磁定位[9]等單一傳感器定位技術及多種傳感器融合定位技術。文獻[10]在城市街道、長距離隧道等復雜非暴露空間,采用全球衛星導航系統(global navigation satellite system, GNSS)/INS/里程計融合的定位方法,極大增加了定位的成功率,除長距離隧道外,定位精度可保持優于2 m。文獻[11]首次將UWB與INS進行了組合并用于確定組合系統的姿態。文獻[12]利用UWB定位技術和行人航位推算(pedestrian dead reckoning, PDR)算法結合,采用約束卡爾曼濾波器使最終行人動態定位精度達到亞米級。文獻[13]針對UWB無線信號易受干擾的問題,提出基于平方根容積卡爾曼濾波先更新后修正測量噪聲的方法,能有效提高UWB/PDR組合的定位精度和穩定性。文獻[14]利用擴展卡爾曼濾波對UWB和PDR進行融合,有效提升了室內定位精度,可以達到分米級。基于UWB的室內單點定位精度高但易受非視距(non line of sight, NLOS)誤差影響,定位結果不穩定,而PDR算法短距離內定位精度高但存在航向漂移,因此將UWB和慣性傳感器組合起來,組成UWB/PDR融合定位系統,二者具有很好的互補性。現階段對UWB/PDR融合定位的研究多集中在削弱UWB NLOS誤差上,如何保持復雜環境下的定位精度和穩定性是一直存在的難題。
在UWB NLOS環境下,UWB/PDR松組合會將NLOS誤差引入UWB定位結果,而在UWB基站信號缺失的環境下,UWB會存在位置信息缺失的情況,從而降低整體融合精度。為了更加充分利用UWB測距信息,保持復雜環境下UWB/PDR融合系統定位的穩定性和精度,本文利用UWB測距及慣性傳感器信息,提出了一種改進的UWB/PDR緊組合的定位方法。與松組合不同,該方法直接對UWB測距值進行融合,不須單獨解算UWB位置信息,在UWB NLOS環境下和UWB基站信號缺失等復雜環境下定位效果都要優于UWB/PDR松組合,而且增加了系統的魯棒性。
1 UWB測距及定位
1.1 UWB測距
UWB 基于到達時間(time of arrival, TOA)測距是通過記錄超寬帶脈沖信號從UWB移動站到基準站傳播的時間來計算UWB移動站到基準站之間的距離。對于室內定位,由于實驗環境等限制,UWB基站高程方向上差異較小造成高程方向出現明顯的定位誤差[15]。所以本文研究主要針對平面位置解算,將UWB基準站固定,保持高度不變;實驗在室內小范圍內進行,UWB移動站高度變化也可忽略不計。計算過程中,在原始TOA測距信息中減去UWB基準站與移動站之間的高差得到平距,其計算公式為
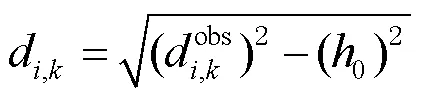
UWB基準站與移動站之間的TOA測距模型為
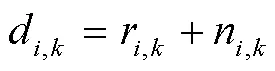
1.2 UWB定位
由UWB TOA測距可得UWB定位表達式為
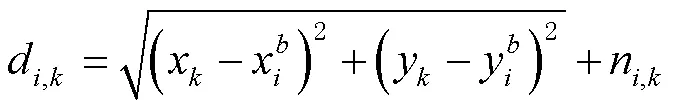
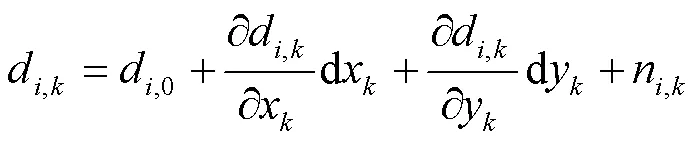
變形可得UWB定位線性觀測方程
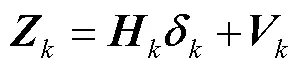
設置迭代閾值,其最小二乘算法解為
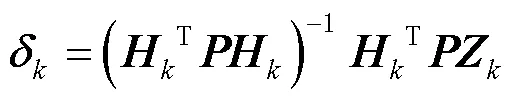
式中為權陣。
最終得到時刻UWB的位置信息為
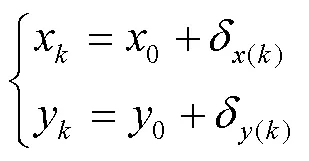
2 行人航位推算
PDR是一種針對行人平面定位導航的相對定位算法[16],其基本原理如圖1所示:利用加速度計和陀螺儀信息,實時探測行人步頻,估計行人步長,同時解算行人航向角;基于行人前一步的位置信息,結合當前時刻的步長和航向角,推算當前時刻行人的位置信息。
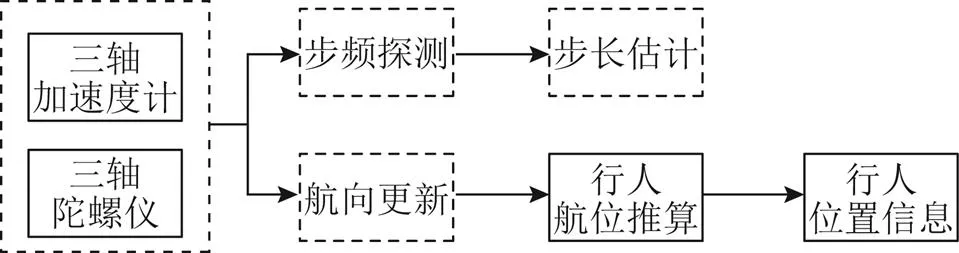
圖1 行人航位推算原理
基本公式為
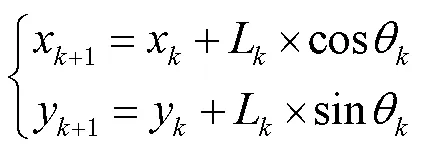
考慮到慣性傳感器的精度和與步長估計算法的同步性,步頻探測算法選取文獻[17]提出的基于“滑動窗口+峰值探測+零點交叉”的算法。此算法先對加速度的重力分量進行剔除,再進行預設窗口的平滑,可有效抑制加速度計隨機噪聲的影響,得到更加明顯的行人步態特征。進行加速度峰值探測時,應保證連續2個加速度峰值之間的時間差大于1個閾值,該閾值大概為行人步行一步的時間,消除同一步里出現加速度多峰造成錯誤的步頻判斷。零點交叉主要用于確定每一跨步的開始點和結束點,即加速度前一時刻小于零,當前時刻大于或等于零的時間。
行人步長模型采用經典步長線性模型[18]:

初始航向角的獲取則利用軌跡相似性原理[19],基于行人1個跨步內航向基本保持不變,通過匹配UWB和PDR的位移向量對MEMS進行航向的初始對準,無須引入額外傳感器。
3 改進的UWB/PDR緊組合算法
目前常用的融合估計方法是利用卡爾曼濾波(Kalman filter,KF)[20]算法對系統進行濾波處理。KF是以一種“預測-更新”的模式對狀態向量進行估計。在預測階段,根據系統狀態方程,遞推狀態預測向量;在量測更新階段,根據系統狀態協方差矩陣和量測噪聲協方差矩陣來計算增益矩陣,然后利用增益矩陣對參數驗前估值和新的觀測值加權平均進行狀態參數更新,從而獲得最優解。然而,在現實應用中很多問題并不能用線性函數表述,通常采用擴展卡爾曼濾波(extend Kalman filter, EKF),即式(10)解決非線性函數問題,主要思想是對非線性函數泰勒級數展開,忽略高階項,將非線性函數近似為線性函數求解,即

3.1 狀態方程
在改進的UWB/PDR 緊組合定位系統中,以UWB建立的坐標系為導航坐標系,以位置誤差、步長誤差和航向角誤差作為系統的狀態變量,即
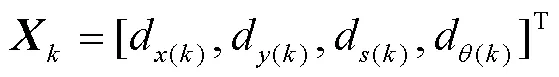
對式(8)進行微分得到UWB/PDR緊組合的狀態方程為
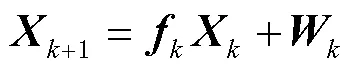
3.2 量測方程
當UWB系統測距信息更新時,以UWB的測距信息和PDR推算的測距信息的差值作為系統量測信息,UWB/PDR緊組合定位系統的量測方程為
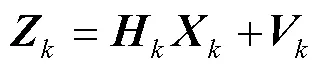
3.3 UWB NLOS檢驗
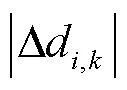
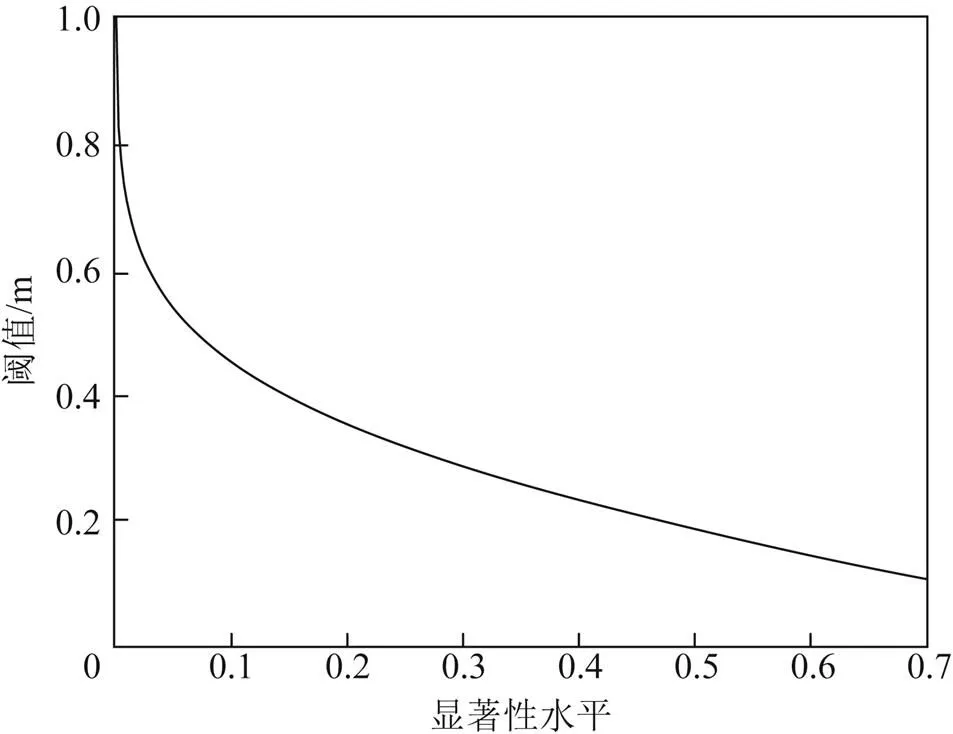
圖2 顯著性水平與閾值之間的關系
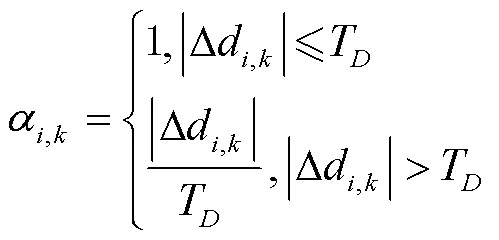


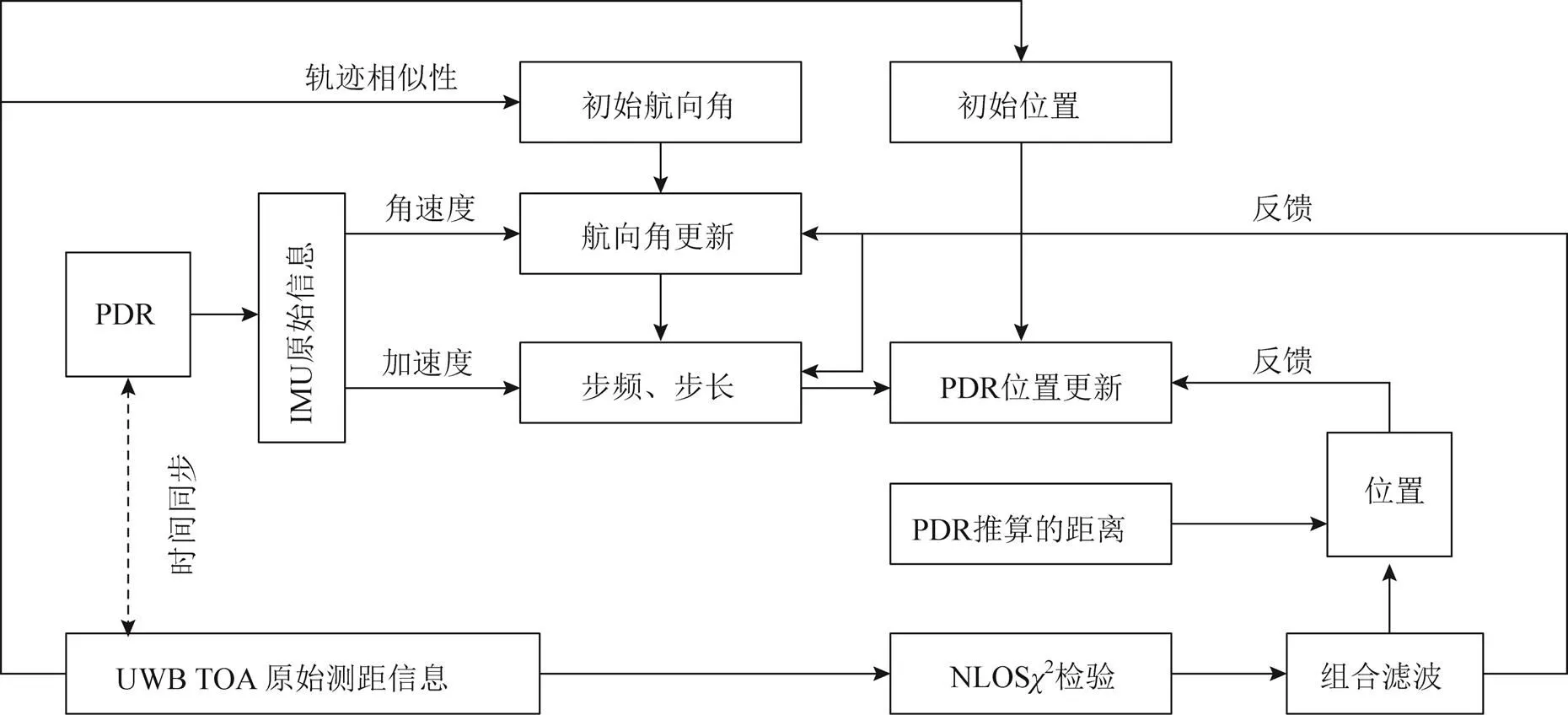
圖3 UWB/PDR緊組合定位流程
4 實驗與結果分析
4.1 實驗條件
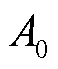

圖4 實驗場地

圖5 原始UWB測距和慣性傳感器信息
4.2 UWB/PDR緊組合
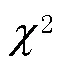
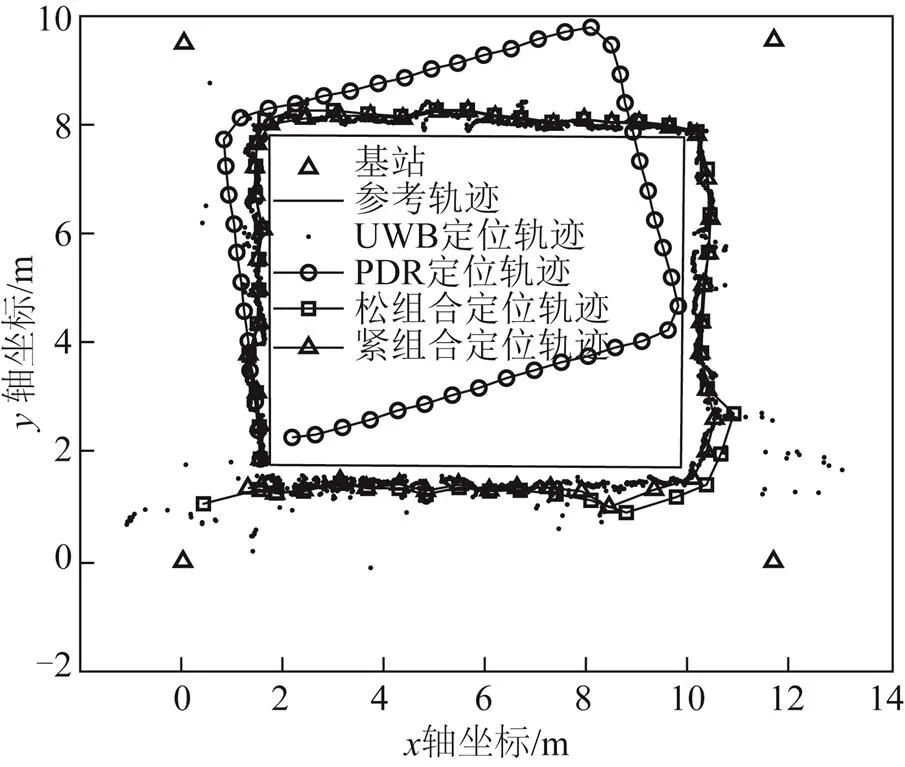
圖6 不同定位方法的定位軌跡結果
圖7展示了上述幾種定位方法的定位誤差。圖8展示了根據定位誤差求得的平面位置誤差累積分布函數(cumulative distribution function,CDF)曲線。表1展示了行人室內定位實驗總體誤差的統計結果。上述結果表明:在視距環境下,改進的UWB/PDR緊組合定位精度與UWB/PDR松組合定位、UWB單獨定位基本一致;而在NLOS環境下,改進的UWB/PDR緊組合最大定位誤差和平均定位誤差分別為0.727和0.669 m,相比于單獨UWB定位的最大誤差和平均誤差分別降低了75.1%和70.1%,相比于PDR定位分別降低了74.5%和62.0%,相比于UWB/PDR松組合分別降低了51.4%和47.7%。因此,改進的UWB/PDR緊組合方法更加充分利用了UWB的測距信息,整體定位效果優于UWB/ PDR松組合,具有較強的魯棒性。
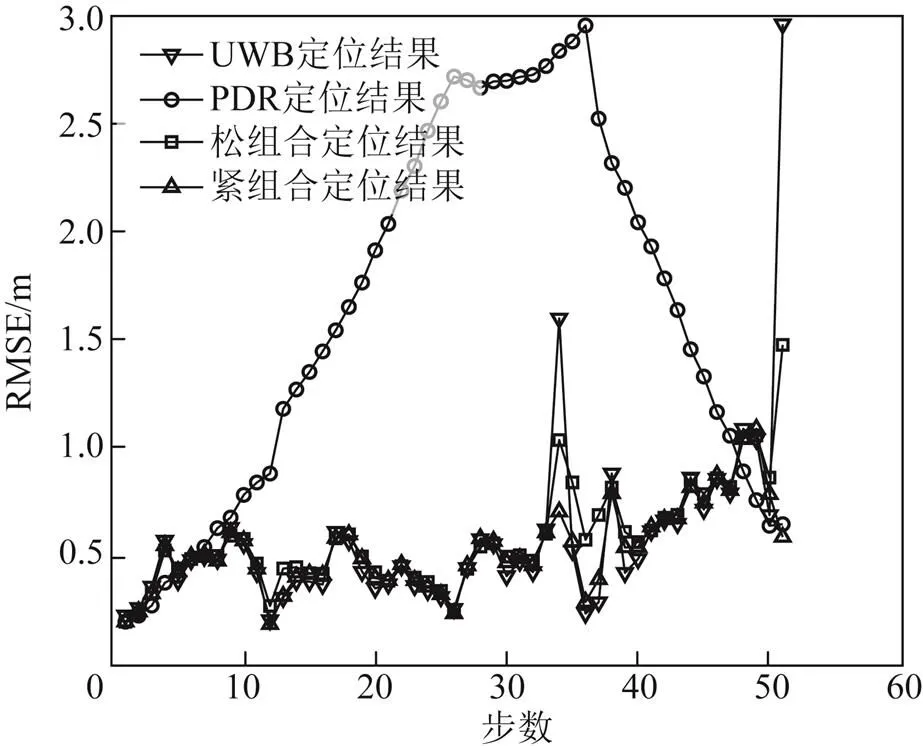
圖7 不同定位方法的的定位誤差
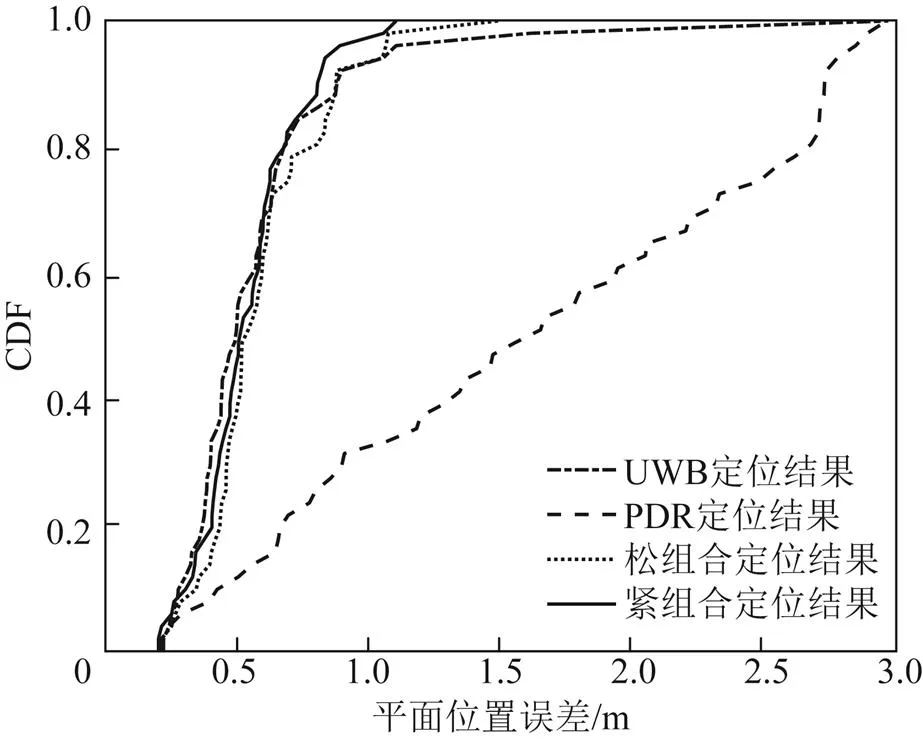
圖8 不同定位方法的位置誤差CDF

表1 不同定位方法的的定位誤差 m
此外,實驗還模擬計算了不同UWB基站數量情況下的UWB/PDR緊組合定位效果。圖9展示了不同UWB基站數量情況下UWB/PDR緊組合定位的軌跡。圖10展示了不同UWB基站數量情況下UWB/PDR緊組合的定位誤差。表2展示了不同UWB基站數量情況下UWB/PDR緊組合定位誤差的統計結果。結果顯示:當UWB基站為4個或3個時,定位效果基本一致;當UWB基站為2個時,部分時刻UWB/PDR緊組合定位效果不如UWB基站為4個或3個時,但整體定位效果還是能夠滿足基本的平面位置估計要求。但由于UWB平面位置解算至少需要3個UWB基站,此時UWB/PDR松組合就不能發揮作用,再次說明UWB/PDR緊組合的魯棒性。當UWB基站數量為1個時,UWB/PDR緊組合定位也會失去對PDR漂移誤差的約束作用,定位誤差也會迅速發散。
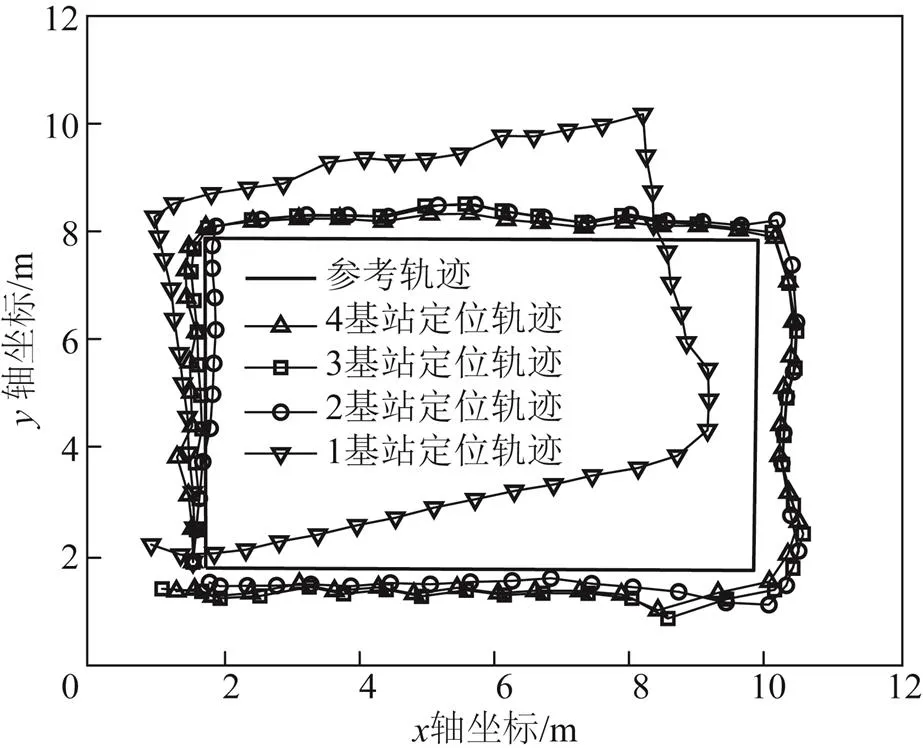
圖9 不同基站數量情況下的緊組合定位軌跡結果
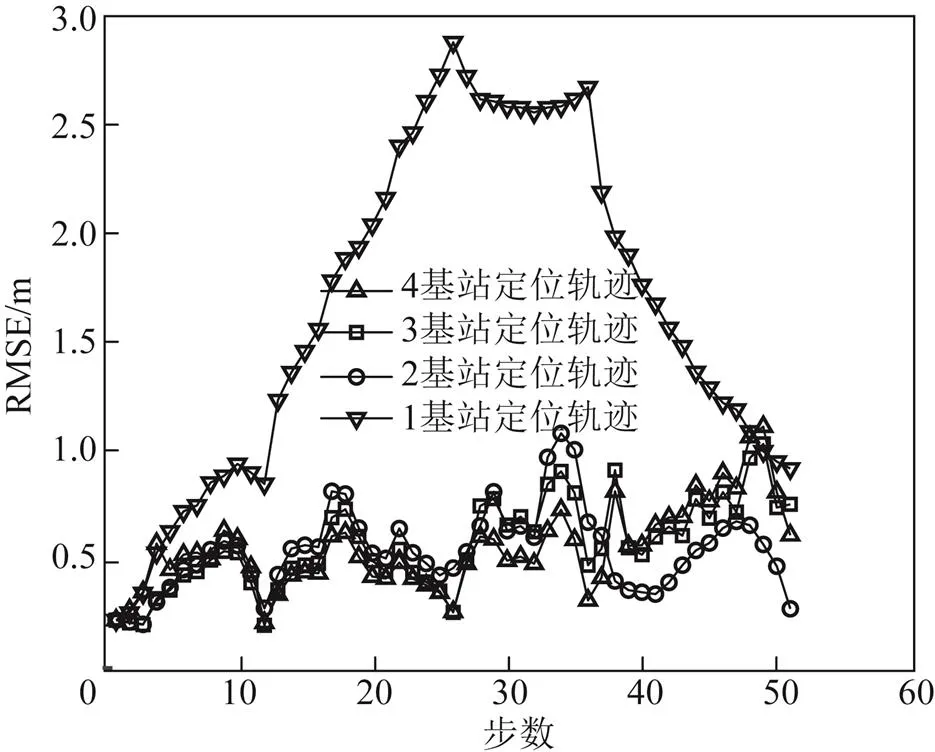
圖10 不同基站數量情況下的緊組合定位誤差

表2 不同基站數量情況下的緊組合定位誤差
最后實驗評估了UWB基站數量缺失情況下行人改進UWB/PDR緊組合的室內動態定位精度。圖11展示了UWB基站數量缺失情況下UWB/PDR松、緊組合定位的軌跡結果。圖12展示了UWB基站數量缺失情況下UWB/PDR松、緊組合定位方法的誤差。結果表明,在UWB基站數量缺失情況下,UWB/PDR緊組合定位效果明顯優于UWB/PDR松組合,特別是在當UWB基站數量為1或2個時。此時,松組合定位退化為單PDR定位,定位誤差迅速增大;UWB/PDR緊組合定位可以充分利用UWB的測距信息,定位精度依然保持在0.6 m左右,具有較強的抗干擾性。圖13展示了根據定位誤差求得的平面位置誤差CDF曲線,結果表明:在UWB基站數量缺失情況下,UWB/PDR緊組合整體定位性能要優于UWB/PDR松組合和單獨PDR;在UWB基站數量變化情況下,UWB/PDR緊組合最大定位誤差和平均定位誤差分別為1.283和0.566 m,相比于UWB/PDR松組合,定位誤差RMS分別降低了18.7%和24.7%,更適合復雜環境的位置估計。
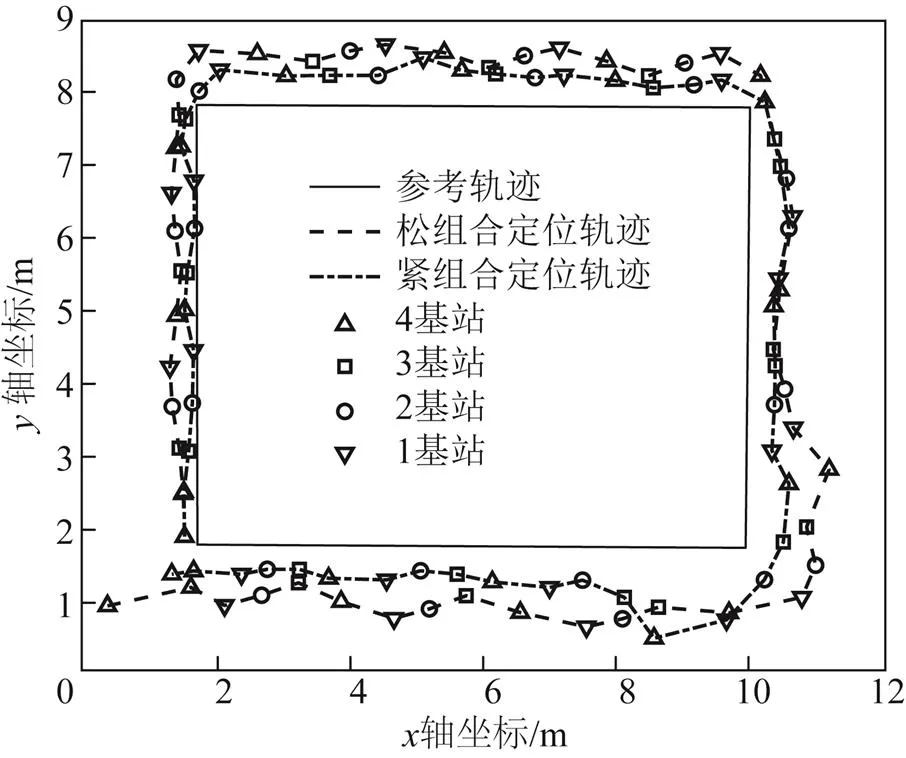
圖11 基站數量缺失情況下的定位軌跡結果
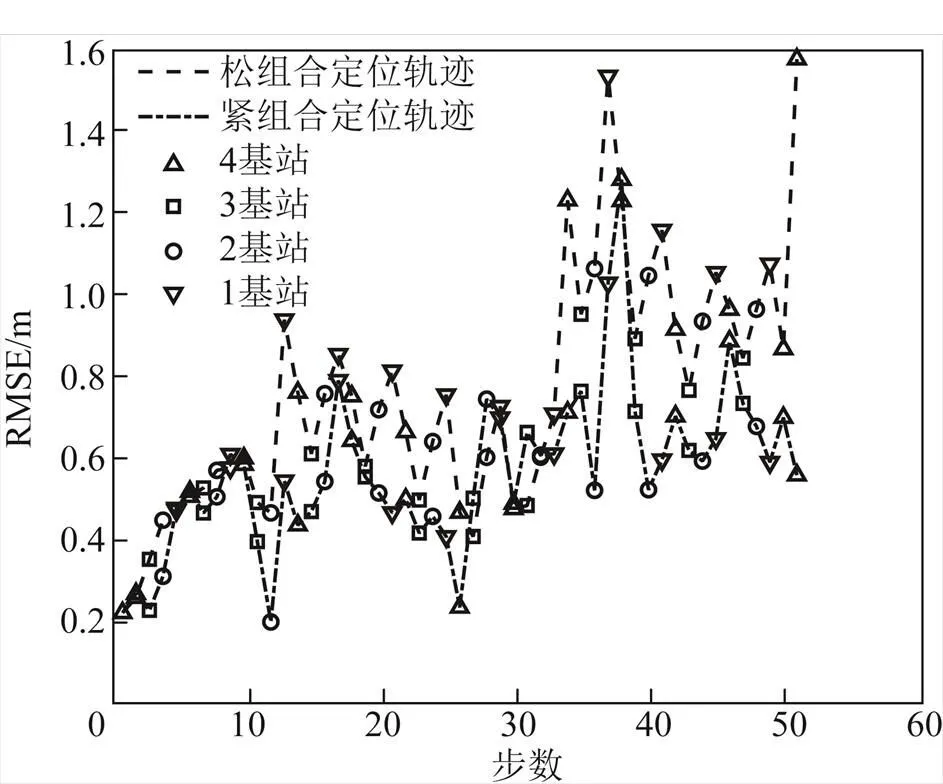
圖12 基站數量缺失情況下的定位誤差
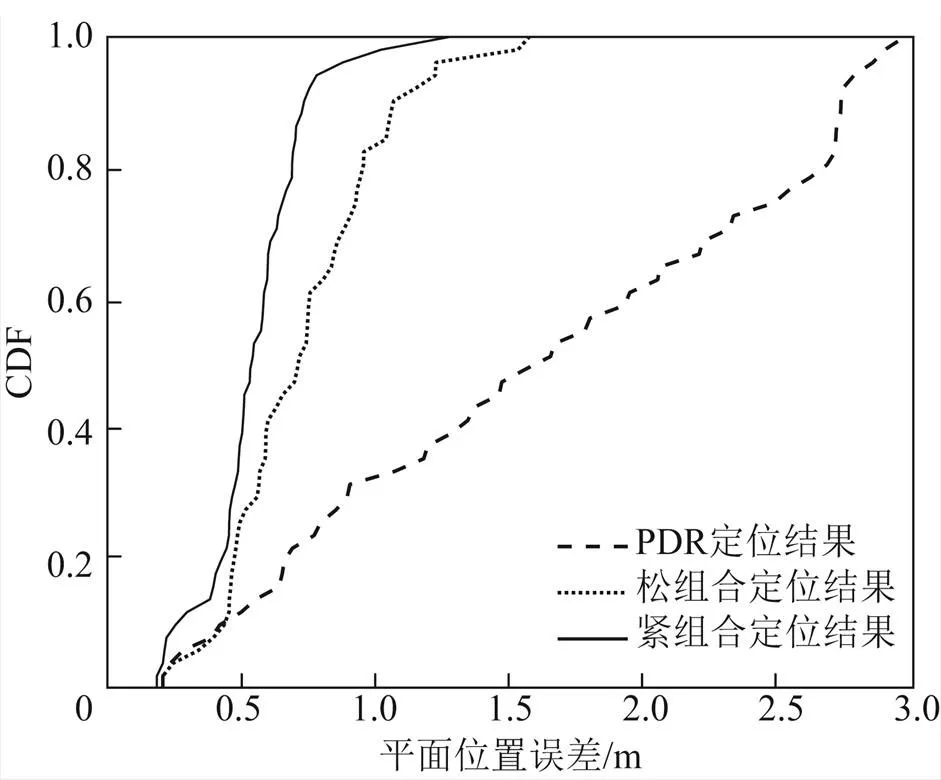
圖13 基站數量缺失情況下的位置誤差累積分布函數
5 結束語
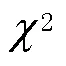
[1] 劉公緒, 史凌峰. 室內導航與定位技術發展綜述[J]. 導航定位學報, 2018, 6(2): 7-14.
[2] ZHUANG Y,YANG J,LI Y,et al.Smartphone-based indoor localization with bluetooth low energy beacons[J].Sensors, 2016, 16(5): 596.
[3] SHU Y,BO C,SHEN G,et al.Magicol:indoor localization using pervasive magnetic field and opportunistic WiFi sensing[J].IEEE Journal on Selected Areas in Communications, 2015, 33(7): 1443-1457.
[4] 張平, 陳昊. 面向5G的定位技術研究綜述[J]. 北京郵電大學學報, 2018, 41(5): 1-12.
[5] 熊海良. 超寬帶無線通信與定位關鍵技術研究[D]. 西安: 西安電子科技大學, 2011.
[6] BARSHAN B,DURRANT-WHYTE H F.Inertial navigation systems for mobile robots[J].IEEE Transactions on Robotics and Automation, 1995, 11(3): 328-342.
[7] YAN Z,CHU S, DENG L. Visual SLAM based on instance segmentation in dynamic scenes[J]. Measurement Science and Technology, 2021, 32(9): 095113.
[8] DOSTáLEK P,DOLINAY J, VA?EK V. Embedded system for audio source localization based on beamforming[J]. International Journal of Circuits: Systems and Signal Processing, 2012, 6(6): 367-375.
[9] LEE S,CHAE S,HAN D.ILoA:indoor localization using augmented vector of geomagnetic field[J].IEEE Access, 2020, 8: 184242-184255.
[10] 劉飛. 多傳感器融合的高精度無縫定位模型與方法研究[J]. 測繪學報, 2021, 50(12): 1780.
[11] HOL J D,DIJKSTRA F, LUINGE H, et al. Tightly coupled UWB/IMU pose estimation[C]//The Institute of Electrical and Electronic Engineers (IEEE). 2009 IEEE International Conference on Ultra-wideband. Palms Springs: IEEE, 2009: 688-692.
[12] LI Z K,ZHAO L,QIN C B,et al.WiFi/PDR integrated navigation with robustly constrained Kalman filter[J].Measurement Science and Technology, 2020, 31(8): 084002.
[13] TANG C,HE C,DOU L.An IMU/ODM/UWB Joint localization system based on modified cubature Kalman filtering[J].Sensors, 2021, 21(14): 4823.
[14] 李景文, 韋晶閃, 周俊芬, 等. 融合UWB+PDR的室內定位方法改進[J]. 測繪通報, 2022(3): 36-40.
[15] 文鎧.基于超寬帶的室內定位與定向關鍵技術研究[D]. 武漢: 武漢大學, 2020.
[16] 曠儉. 基于捷聯PDR和磁場特征匹配的智能手機多源室內定位算法研究[D]. 武漢: 武漢大學, 2019.
[17] 陳偉.基于GPS和自包含傳感器的行人室內外無縫定位算法研究[D]. 合肥: 中國科學技術大學, 2010.
[18] 陳銳志, 郭光毅, 葉鋒, 等. 智能手機音頻信號與MEMS傳感器的緊耦合室內定位方法[J]. 測繪學報, 2021, 50(2): 143-152.
[19] CHEN Q J,LIN H,GUO R,et al.Rapid and accurate initial alignment of the low-cost MEMS IMU chip dedicated for tilted RTK receiver[J].GPS Solutions, 2020, 24(4): 1-13.
[20] 徐恩松, 陸文華, 劉云飛, 等. 基于卡爾曼濾波的數據融合算法與應用研究[J]. 計算機技術與發展, 2020, 30(5): 143-147.
[21] 苗岳旺, 周巍, 田亮, 等. 基于新息檢測的擴展抗差卡爾曼濾波及其應用[J]. 武漢大學學報(信息科學版), 2016, 41(2): 269-273.
[22] 楊元喜, 任夏, 許艷. 自適應抗差濾波理論及應用的主要進展[J]. 導航定位學報, 2013, 1(1): 9-15.
[23] 陳國良, 李飛, 張言哲. 一種基于自適應波峰檢測的MEMS計步算法[J]. 中國慣性技術學報, 2015, 23(3): 315-321.
Tight integration positioning method of UWB/PDR in complex environments
DAI Xiaoji1, LI Min2, XU Tianhe2, JIANG Nan2, XU Yan2
(1. School of Geological and Surveying Engineering, Chang’an University, Xi’an 710054, China;2. Institute of Space Science, Shandong University, Weihai, Shandong 264209, China)
indoor positioning; ultra wide band; pedestrian dead reckoning; tight integration; complex environments
P228
A
2095-4999(2022)06-0018-09
代曉霽,李敏,徐天河,等. 復雜環境下的UWB/PDR緊組合定位方法[J]. 導航定位學報, 2022, 10(6): 18-26.(DAI Xiaoji, LI Min, XU Tianhe, et al. Tight integration positioning method of UWB/PDR in complex environments[J]. Journal of Navigation and Positioning, 2022, 10(6): 18-26.)
10.16547/j.cnki.10-1096.20220603.
2022-06-17
國家重點研發計劃項目(2020YFB0505800,2020YFB0505804)。
代曉霽(1995—),男,河南駐馬店人,碩士研究生,研究方向為室內定位。
徐天河(1975—),男,湖北黃岡人,博士,教授,研究方向為衛星導航、衛星重力、海洋大地測量基準、海洋自適應融合導航。

