巧哉，質數幻方

肖樂農

幻方的研究由來已久，古老的洛書是研究幻方的最早神話.由于幻方妙趣橫生，吸引著眾多的愛好者，研究成果層出不窮.幻方的種類形形色色：回文幻方、積幻方、雙重幻方、六角幻方、馬步幻方……每一款都構思奇巧，但最巧的是質數幻方.

質數是一種很難駕馭的數.它分布混亂，無窮無盡.可是，數學家們竟然使質數與具有均衡對稱美的幻方聯起手來，巧妙地構造出了一個個質數幻方.

你看，圖１就是一個三階質數幻方.它不但９個數都是質數，而且每行、每列及兩條對角線上的三個數之和都等于２６７.我們來看看構成這個幻方的９個質數：

１１，７１，１３１；２９，８９，１４９；４７，１０７，１６７.

原來這９個質數可分為３組，每組相鄰兩數的差（后一個減前一個數）都是６０，每一組的三個質數都不在同一行、同一列.

怎么樣？挺巧吧．其實，真正的巧事還在后頭.

有一次，一位宮廷數學家領到了一年的工資，共１ ３５０個銀元.他做游戲似地將這些銀元分成不相等的９堆，然后擺成一個幻方，并給國王看了.這是一位很喜歡研究質數和幻方的國王，他看后非常贊賞，但覺得這些堆中沒有一堆是質數，有些遺憾.

這時數學家對國王說：“只要國王獎賞我９個銀元，我在每堆中各加１個銀元，幻方中的每一堆銀元就都是質數了.”國王發現果真如此，就高興地獎賞了數學家９個銀元，并加到幻方之中.

站在旁邊的一個宮女對數學家說：“如果我在每一堆中拿走相同數目的銀元，使幻方中的每一堆仍是質數，您同意我帶走拿出來的銀元嗎？”數學家覺得宮女不懂數學，再加上這事也不太可能，便答應了.于是，宮女從每堆中拿走２個銀元.這時，國王和數學家發現，幻方中剩下的每堆銀元確實都是質數，那１８個銀元只好讓宮女帶走了.

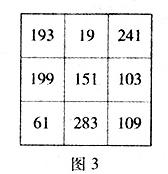
那么，數學家一開始擺的幻方是什么樣呢？以后兩次變化又是怎么樣呢？請看如圖２、圖３、圖４的三個幻方：

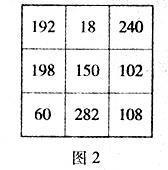
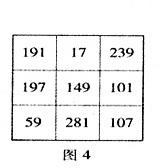
原來后兩個質數幻方是由９對孿生質數構成的，一個由每對孿生質數中較大的那個質數構成，另一個由每對孿生質數中較小的那個質數構成.

質數幻方的排序之巧，構造之難，挑戰著眾多的數學家：美國數學科普大師馬丁·加德納曾懸賞１００美元，獎給第一位利用連續質數造出三階幻方的人.注意，９個質數必須是連續的，中間一個也不許跳過.這道題可夠難的，沒有點功力根本無法辦到.

俗話說重賞之下必有勇夫（可惜不是什么重賞）．１９８８年，美國的一位幻方愛好者納爾遜，利用加利福尼亞大學的克雷超級計算機，通過巧妙的程序設計，一舉解決了這個難題，并且一下子提供了２２個答案，超額完成了任務.其中數字最小的一個如圖５所示.

納爾遜坦言，他的程序并不能證明這是最小解，但要找到更小解的概率幾乎接近于零.