面元法預估導管螺旋槳定常性能的一種簡便方法

海軍工程大學 船舶與動力學院 武漢 430033

導管螺旋槳通過改變螺旋槳槳葉盤面處的來流使螺旋槳獲得較高的效率，被廣泛應用于大型、高負荷的船舶。但是，導管和螺旋槳的相互關系如果處理不好往往會降低推進系統效率，嚴重的還會產生導管振動和空泡剝蝕、噪聲等問題，因此，從理論上預報導管螺旋槳的水動力性能十分重要。

勢流范圍內的導管螺旋槳定常性能預估已有大量研究。比較成熟的是迭代求解法[2-5]，即應用渦格法+面元法[2-4]或面元法+面元法[5,6]分別計算槳和導管的性能，再利用迭代方法使結果達到收斂。

該方法在計算中分別計算槳對導管以及導管對槳的誘導速度，迭代過程花費較多時間，因此，建立一個基于速度勢的面元法+面元法求解均流中導管螺旋槳定常性能的較為簡便的方法。

1 數值方法

1.1 離散化

考慮導管槳在無限大的均勻來流中工作的情況，假設為理想流體，不可壓縮。建立圖1所示直角坐標系o-xyz，x軸與槳軸線重合并以下游為正方向，y軸以垂直向上為正方向，z軸按右手法則確定。槳工作時，導管和槳以VA沿x軸負方向運動，槳葉旋轉速度為Ω。

圖1 導管螺旋槳坐標

應用面元法對導管和螺旋槳求解，計算過程中將槳、導管和槳轂看作一體。螺旋槳、導管和槳轂表面采用四邊形雙曲面元進行離散。對于定常問題，每個槳葉及它泄出的尾渦片所處的情況是相同的。設共有Z個槳葉。如果把槳轂表面周向分成Z個區間，則各區間相互之間亦處于相同情況。因此，只要解決一個葉片及與它連帶的一個槳轂表面區和一個尾流區，那么整個問題就可以解決了。螺旋槳槳葉表面離散為MP×2NPD個面元，其中MP和NPD為徑向和弦向面元數，螺旋槳一個槳葉對應的導管表面離散為NCD×2NXD個面元，其中NCD和NXD分別為周向和軸向面元數，相鄰槳葉間槳轂表面離散為MNW個面元，導管槳單個槳葉對應部分表面總的離散面元為：MPRD=MP×2NPD+NCD×2NXD+MNW導管槳的離散網格如圖2所示。

圖2 導管螺旋槳離散網格

螺旋槳和導管的尾渦采用近似模型。螺旋槳尾渦面具有收縮和螺距變化，導管尾渦面具有收縮，至下游某一指定位置后保持常量至遠下游，槳尾渦面離散為MP×NW個四邊形雙曲面元，導管尾渦面離散為NCD×NDW個四邊形雙曲面元。螺旋槳和導管的尾渦離散網格見圖3、4。

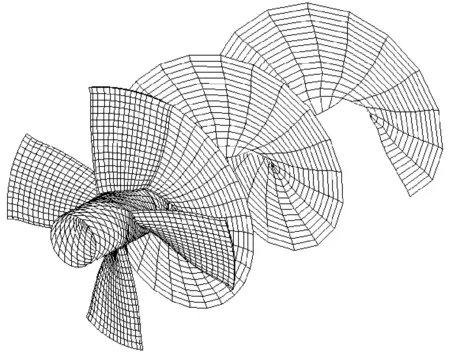
圖3 螺旋槳尾渦離散網格圖

圖4 導管及其尾渦離散網格

槳和導管表面各離散單元均布偶極子和源匯，尾渦面上均布偶極子，各單元的形心為控制點。這樣可以把整個槳表面擾動速度勢方程離散為

(1)

式中：N——單個槳葉以及及葉對應的槳轂和導管表面總的控制點數；

MP——單個槳葉尾渦條帶數；

NCD——單個槳葉對應導管部分尾渦條帶數；

Aij、Wik、Wil、Bij——影響系數。

對于近場，影響系數可通過解析方法積分求得精確解，對于遠場，可通過高斯積分求得近似解。

通過求解線性方程組(1)，可得到導管螺旋槳表面擾動速度勢的值。

1.2 庫塔條件

對槳葉隨邊處和導管分別應用等壓庫塔條件，即要求槳葉臨近隨邊上下面元和導管臨近尾端處上下表面的控制點處有相等的壓力。槳葉和導管的庫塔條件如下式：

(2)

Δpk=pU-pL=0k=1,2,…,NCD

(3)

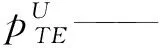
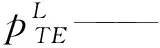
pU——導管臨近尾端內側面元所受壓力；

pL——導管臨近尾端外側面元所受壓力。

分別采用Newton-Raphson迭代方法進行迭代求解，求解時ΔΦ的初值取Morino線性庫塔條件的值。

1.3 槳的推力和轉矩

螺旋槳和導管的推力和轉矩可通過求解槳葉槳轂和導管表面的壓力分布并計及粘性阻力分量來得到。由壓力分布積分可得到推力和轉矩的公式：

式中：pi——物面上某面元形心處的壓力。

槳葉的粘性阻力計算如下，CD取0.004 5。

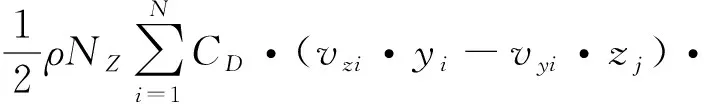
|vi|·ΔSi

2 數值計算結果

應用本方法對簡易導管槳系列進行了計算，改系列槳包括JD7704+Ka系列和JD75+Ka系列兩組槳，導管和螺旋槳的幾何參數和實驗數據見文獻[6]。計算中每個槳葉弦向和展向面元數取為16×16，為均勻劃分，導管周向和弦向面元數取為40×36，為均勻劃分。

圖5～9是利用本方法計算結果與試驗結果[6]的比較。

可以看出，在較大的進速系數范圍內總推力和轉矩的計算結果與實驗結果吻合較好，導管推力在槳工作狀態左右與試驗結果吻合較好，但在載荷較重時計算結果偏低。

圖5 JD7704導管+Ka4-70(P/D=1.0)槳敞水性能比較

圖6 JD7704導管+Ka4-55(P/D=1.0)槳敞水性能比較

圖7 JD7704導管+Ka4-70(P/D=0.8)槳敞水性能比較

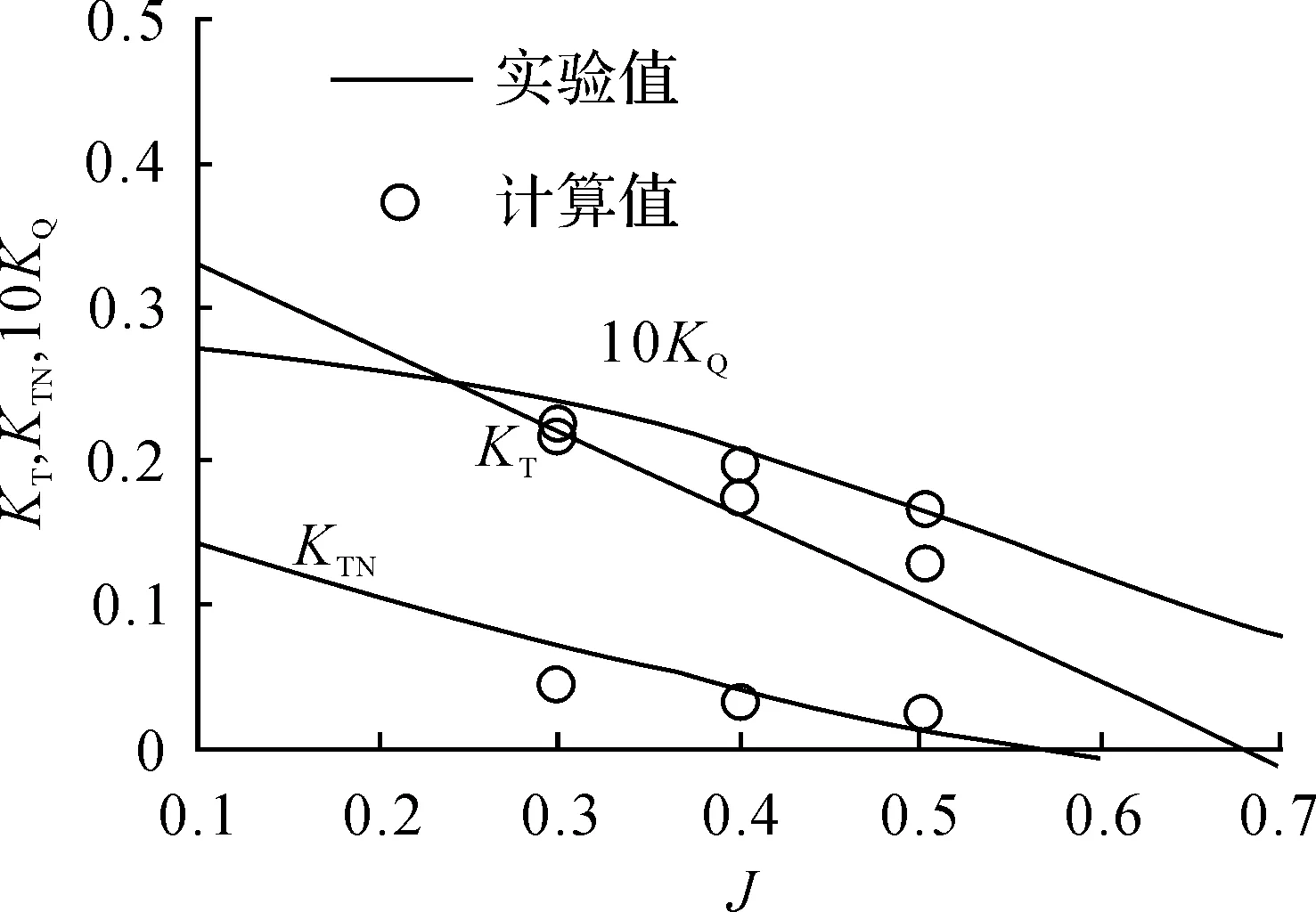
圖8 JD7704導管+Ka4-55(P/D=0.8)槳敞水性能比較

圖9 JD75導管+Ka4-70(P/D=1.0)槳敞水性能比較

3 結論

本文提供的基于速度勢的低階面元法求解導管螺旋槳定常性能的方法與傳統的迭代方法相比所不同的是，該方法將導管和螺旋槳的相互影響計入求解影響系數的過程中，求解時將槳和導管看作一個整體，不用求解導管對槳或槳對導管的誘導速度，避免了迭代過程，使計算時間大大縮減，所得到的結果能夠達到比較滿意的精度。

[1] Kinnas S A, Hsin C Y, Keenan D P. A Potential Based Panel Method for the Unsteady Flow around Open and Ducted Propellers[A]. 18th ONR[C]. Ann Arbor, Michigan, 1990：21-38．

[2] 蔣志超，王國強，楊晨俊. 導管面元網格劃分和影響系數計算的研究[J].船舶力學，2000，10(5)：1-8．

[3] 楊晨俊，王國強，楊建民. 導管螺旋槳定常性能理論計算[J].上海交通大學學報，1997，11(11)：36-39．

[4] Zhang J H, Wang G Q. Prediction of hydrodynamic performances of ducted controllable pitch propeller[J]. Journal of ship Mechanics, 2002,6(6):18-27．

[5] Liu X L, Wang G Q. A Potential Based Panel Method for Prediction of Steady Performance of Ducted propeller[J]. Journal of ship Mechanics, 2006，6(3):26-35．

[6] 盛振邦. 楊家盛，柴楊業，中國船用螺旋槳系列試驗圖譜集[M].上海：中國造船編輯部，1983．

[7] 譚廷壽. 面元法預報螺旋槳水動力性能[J]. 武漢交通科技大學學報，1997，10(5)：534～541．

[8] 熊 鷹. 非均勻流中螺旋槳空泡即脈動壓力的數值和試驗研究[D]. 武漢：武漢理工大學，2002．

[9] 葉金銘.考慮自由液面和船體邊界條件的螺旋槳脈動壓力研究[D].武漢： 海軍工程大學，2003．