高等教育質(zhì)量工程:回顧與反思
袁海軍
[摘 要] “高等教育質(zhì)量工程”是20世紀(jì)90年代以來(lái)國(guó)家組織實(shí)施的一系列高等學(xué)校教學(xué)改革和質(zhì)量建設(shè)計(jì)劃的總稱。根據(jù)目標(biāo)和任務(wù)的不同,這項(xiàng)計(jì)劃可劃分為“教改工程”“質(zhì)量工程”和“本科教學(xué)工程”三個(gè)時(shí)期,每個(gè)時(shí)期又依據(jù)一些標(biāo)志性事件劃分為若干階段。“高等教育質(zhì)量工程”的實(shí)施,在鞏固高校教學(xué)工作中心地位、推動(dòng)高校加大對(duì)教學(xué)工作的投入等方面發(fā)揮了重要作用,但也存在著“效率”與“公平”“項(xiàng)目化管理”與“常規(guī)管理”“最好的教育”與“適合的教育”等深層次觀念的沖突,需要及時(shí)化解。近期發(fā)布的“普通高等學(xué)校本科專業(yè)類教學(xué)質(zhì)量國(guó)家標(biāo)準(zhǔn)”是“高等教育質(zhì)量工程”最重要的成果之一,按照國(guó)家有關(guān)規(guī)定重新啟動(dòng)再標(biāo)準(zhǔn)化進(jìn)程,是增強(qiáng)其地位和功能的首要任務(wù)。
[關(guān)鍵詞] 高等教育質(zhì)量工程;本科教學(xué);國(guó)標(biāo);再標(biāo)準(zhǔn)化
[中圖分類號(hào)] ??G640 ?[文獻(xiàn)標(biāo)識(shí)碼] ?A ?[文章編號(hào)] 1005-5843(2019)01-0001-10
[DOI] 10.13980/j.cnki.xdjykx.2019.01.001
隨著“普通高等學(xué)校本科專業(yè)類教學(xué)質(zhì)量國(guó)家標(biāo)準(zhǔn)”(下文簡(jiǎn)稱“國(guó)標(biāo)”)的正式發(fā)布,歷時(shí)20多年的“高等教育質(zhì)量工程”也告全面竣工。那么,“高等教育質(zhì)量工程”與“國(guó)標(biāo)”之間是什么關(guān)系,它的實(shí)施對(duì)我國(guó)高等學(xué)校本科教學(xué)質(zhì)量產(chǎn)生了哪些積極影響?對(duì)此,有必要深入了解“高等教育質(zhì)量工程”的發(fā)生、發(fā)展歷程,揭示其歷史貢獻(xiàn)與時(shí)代局限,同時(shí)按照國(guó)家有關(guān)規(guī)定積極推進(jìn)“國(guó)標(biāo)”的再標(biāo)準(zhǔn)化建設(shè),這是當(dāng)前高校深化教學(xué)改革、加快質(zhì)量建設(shè)的現(xiàn)實(shí)要求。
一、對(duì)“高等教育質(zhì)量工程”的回顧
“高等教育質(zhì)量工程”在很多場(chǎng)合又被稱為“質(zhì)量工程”,因此“質(zhì)量工程”這一概念有狹義和廣義之分。狹義的“質(zhì)量工程”是指2007年教育部、財(cái)政部推出的“高等學(xué)校本科教學(xué)質(zhì)量與教學(xué)改革工程”,而廣義的“質(zhì)量工程”還包括“十二五”時(shí)期的“本科教學(xué)工程”;進(jìn)一步回溯,2004年2月《教育部2003—2007年教育振興行動(dòng)計(jì)劃》提出的“高等學(xué)校教學(xué)質(zhì)量與教學(xué)改革工程”也一度被稱為“質(zhì)量工程”;而要追根溯源,則要上溯到20世紀(jì)90年代初原國(guó)家教委組織實(shí)施的“高等教育面向21世紀(jì)教學(xué)內(nèi)容和課程體系改革計(jì)劃”及21世紀(jì)初教育部實(shí)施的“新世紀(jì)高等教育教學(xué)改革工程”。為論述方便,筆者用“質(zhì)量工程”一詞專指2007年至2011年間實(shí)施的“高等學(xué)校本科教學(xué)質(zhì)量與教學(xué)改革工程”,而用“高等教育質(zhì)量工程”來(lái)泛指1994年以來(lái)國(guó)家實(shí)施的一系列教學(xué)改革和質(zhì)量建設(shè)計(jì)劃。為保持歷史原貌,這些計(jì)劃的名稱不論全稱還是簡(jiǎn)稱,都沿用了當(dāng)時(shí)的提法。
(一)1994—2006年:“教改工程”時(shí)期
在新舊世紀(jì)之交的十多年間,我國(guó)高教發(fā)展的主題之一是深化高校教學(xué)內(nèi)容和課程體系改革,史稱“教改工程”。“教改工程”分三個(gè)階段實(shí)施。
1. “教學(xué)內(nèi)容改革計(jì)劃”階段(1994—1999年)。“教學(xué)內(nèi)容改革計(jì)劃”的全稱是“高等教育面向21世紀(jì)教學(xué)內(nèi)容和課程體系改革計(jì)劃”,是1994年原國(guó)家教委為遏制高校教學(xué)質(zhì)量滑坡、促進(jìn)教學(xué)工作升溫而推出的一項(xiàng)全國(guó)性教學(xué)改革方案。這一時(shí)期,高校教學(xué)工作的中心地位在市場(chǎng)經(jīng)濟(jì)大潮沖擊下受到大幅動(dòng)搖,教育質(zhì)量出現(xiàn)大面積的嚴(yán)重滑坡跡象。原國(guó)家教委有關(guān)領(lǐng)導(dǎo)將其概括為“三種滑坡現(xiàn)象”(有的學(xué)校出現(xiàn)了滑坡局面,有的呈現(xiàn)滑坡趨勢(shì),有的存在滑坡的潛在危險(xiǎn))和“四個(gè)投入不足”(經(jīng)費(fèi)投入不足,領(lǐng)導(dǎo)精力投入不足,部分教師和學(xué)生對(duì)教學(xué)投入不足)[1][2]。為有效控制教育質(zhì)量滑坡局面,原國(guó)家教委于1994年6月10日印發(fā)了《關(guān)于加強(qiáng)普通高等學(xué)校教學(xué)工作的意見(jiàn)》(教高[1994]10號(hào)),首次提出實(shí)施“面向21世紀(jì)教學(xué)內(nèi)容改革計(jì)劃”的設(shè)想。經(jīng)過(guò)充分論證,先后在文、理、工、農(nóng)林、醫(yī)藥、經(jīng)濟(jì)和法學(xué)等6大科類范圍內(nèi)批準(zhǔn)了211個(gè)項(xiàng)目、985個(gè)子項(xiàng)目,籌集經(jīng)費(fèi)700萬(wàn)元資助項(xiàng)目建設(shè)。有關(guān)部委也資助100多萬(wàn)元支持教改立項(xiàng)工作。1997年,原國(guó)家教委印發(fā)了《關(guān)于組織實(shí)施“高等師范教育面向21世紀(jì)教學(xué)內(nèi)容和課程體系改革計(jì)劃”的通知》(教師[1997]3號(hào)),將高等師范教育也納入了“教學(xué)內(nèi)容改革計(jì)劃”,實(shí)現(xiàn)了對(duì)主要學(xué)科門(mén)類的全覆蓋。這項(xiàng)計(jì)劃涉及高校教學(xué)工作的主要環(huán)節(jié),包括人才培養(yǎng)模式、專業(yè)培養(yǎng)目標(biāo)和規(guī)格、教學(xué)計(jì)劃和課程結(jié)構(gòu)、教材編寫(xiě)和出版、教學(xué)方法和手段等。因其“有組織、較系統(tǒng)、起點(diǎn)高、立意新、整體性強(qiáng)”等特點(diǎn)[3],受到全國(guó)高校和廣大教師的高度重視,總共有322所高校、10 256位教師和管理人員參與了項(xiàng)目研究,推出了一系列人才培養(yǎng)新方案和高質(zhì)量統(tǒng)編教材[4]。這種由國(guó)家頂層規(guī)劃、統(tǒng)籌管理,高等學(xué)校積極參與、立項(xiàng)研究的教改形式,首開(kāi)“高等教育質(zhì)量工程”先河,其影響與作用一直延續(xù)至今。
2. “新世紀(jì)教改工程”階段(2000—2003年)。2000年1月26日,教育部印發(fā)了《關(guān)于實(shí)施“新世紀(jì)高等教育教學(xué)改革工程”的通知》(教高[2000]1號(hào)),正式啟動(dòng)“新世紀(jì)高等教育教學(xué)改革工程”(簡(jiǎn)稱“新世紀(jì)教改工程”)。從時(shí)段上看,“新世紀(jì)教改工程”是20世紀(jì)“教學(xué)內(nèi)容改革計(jì)劃”的延續(xù)。這項(xiàng)工程包括6大教改項(xiàng)目:高等教育人才培養(yǎng)戰(zhàn)略規(guī)劃研究、高等學(xué)校本科教育教學(xué)改革與實(shí)踐、高職高專教育教學(xué)改革與實(shí)踐、現(xiàn)代遠(yuǎn)程教育資源建設(shè)、高校中青年骨干教師培訓(xùn)、高校基礎(chǔ)教學(xué)實(shí)驗(yàn)室改造與建設(shè)等。其中,“本科教育教學(xué)改革與實(shí)踐計(jì)劃”審批研究項(xiàng)目670個(gè),建成各類“基礎(chǔ)學(xué)科建設(shè)和人才培養(yǎng)基地”近200個(gè),有265所高校承擔(dān)了研究任務(wù),經(jīng)費(fèi)總投入達(dá)2 530萬(wàn)元[5]。作為“新世紀(jì)教改工程”的組成部分,教育部還啟動(dòng)了“世行貸款高等教育發(fā)展項(xiàng)目”之軟課題“21世紀(jì)初高等教育教學(xué)改革項(xiàng)目”,批準(zhǔn)立項(xiàng)336個(gè),其中理工類266個(gè)、醫(yī)藥類70個(gè),資助經(jīng)費(fèi)總額300萬(wàn)元。此外,教育部還實(shí)施了“新世紀(jì)高職高專教育人才培養(yǎng)模式和教學(xué)內(nèi)容體系改革與建設(shè)項(xiàng)目計(jì)劃”,批準(zhǔn)34個(gè)項(xiàng)目,選題涉及人才培養(yǎng)模式研究、專業(yè)大類人才培養(yǎng)模式與教學(xué)內(nèi)容體系改革、基礎(chǔ)課程教學(xué)內(nèi)容與課程體系改革等。
3. “高等學(xué)校教學(xué)質(zhì)量與教學(xué)改革工程”階段(2004—2006年)。2004年2月,國(guó)務(wù)院批轉(zhuǎn)了《教育部2003—2007年教育振興行動(dòng)計(jì)劃》(國(guó)發(fā)[2004]5號(hào)),同時(shí)啟動(dòng)“高等學(xué)校教學(xué)質(zhì)量與教學(xué)改革工程”。這項(xiàng)工程規(guī)劃項(xiàng)目12個(gè),實(shí)際啟動(dòng)4個(gè)[6]:(1)“精品課程”項(xiàng)目,3年內(nèi)共建成國(guó)家級(jí)精品課程1 100多門(mén),并為它們授予了榮譽(yù)稱號(hào);(2)“教學(xué)名師獎(jiǎng)”項(xiàng)目,3年中分兩批授予200名教師“國(guó)家級(jí)高等學(xué)校教學(xué)名師”榮譽(yù)稱號(hào),其待遇相當(dāng)于同級(jí)同類科技獎(jiǎng);(3)大學(xué)英語(yǔ)教學(xué)改革項(xiàng)目,共有400多所高校的200多萬(wàn)名學(xué)生參與了計(jì)算機(jī)個(gè)性化、交互式學(xué)習(xí)等項(xiàng)目;(4)高等學(xué)校教學(xué)評(píng)估項(xiàng)目,確立了“五年一輪”評(píng)估制度及普通高校教學(xué)狀態(tài)數(shù)據(jù)采集和發(fā)布制度。此外,還建成了84個(gè)國(guó)家級(jí)實(shí)驗(yàn)教學(xué)示范中心及全國(guó)網(wǎng)絡(luò)教育公共服務(wù)體系、數(shù)字化圖書(shū)館與優(yōu)質(zhì)資源共享系統(tǒng)等。盡管時(shí)間不長(zhǎng),但立意高遠(yuǎn)、設(shè)計(jì)科學(xué),多數(shù)教改項(xiàng)目都得到繼承,甚至連“質(zhì)量工程”這一縮略用法也被沿用了下來(lái)[7]。
(二)2007—2010年:“質(zhì)量工程”時(shí)期
2007年1月22日,教育部、財(cái)政部印發(fā)了《關(guān)于實(shí)施“高等學(xué)校本科教學(xué)教學(xué)質(zhì)量與教學(xué)改革工程”的意見(jiàn)》(教高[2007]1號(hào)),正式啟動(dòng)“高等學(xué)校本科教學(xué)質(zhì)量與教學(xué)改革工程”(簡(jiǎn)稱“質(zhì)量工程”)。“質(zhì)量工程”首次聚焦“本科教學(xué)”,并帶有高等教育轉(zhuǎn)型期的鮮明時(shí)代烙印。
1. 工程建設(shè)服務(wù)于高等教育發(fā)展模式轉(zhuǎn)型。在世紀(jì)之交的數(shù)年間,我國(guó)高校連年擴(kuò)招導(dǎo)致高教規(guī)模急劇擴(kuò)張。2006年,全國(guó)普通高校招生540萬(wàn)人,是1998年的5倍;在校生總?cè)藬?shù)2 500萬(wàn)人,是1998年的4倍;毛入學(xué)率達(dá)到22%,進(jìn)入了國(guó)際公認(rèn)的大眾化階段。在高等教育實(shí)現(xiàn)跨越式發(fā)展的同時(shí),也帶來(lái)了基礎(chǔ)建設(shè)投入不足、教學(xué)質(zhì)量下滑、畢業(yè)生就業(yè)困難等一系列問(wèn)題。為此,國(guó)務(wù)院在2006年5月10日召開(kāi)的第135次常務(wù)會(huì)議上做出了控制招生幅度增長(zhǎng)、穩(wěn)定招生規(guī)模、切實(shí)把發(fā)展重點(diǎn)放在提高質(zhì)量上的重要決定。同年8月29日,時(shí)任中共中央總書(shū)記胡錦濤在政治局第34次集體學(xué)習(xí)時(shí)再次強(qiáng)調(diào):“普及和鞏固義務(wù)教育,大力發(fā)展職業(yè)教育,提高高等教育質(zhì)量,是‘十一五規(guī)劃綱要對(duì)教育事業(yè)發(fā)展提出的三項(xiàng)主要任務(wù),必須切實(shí)抓實(shí)抓好。”[8]為落實(shí)中央部署,教育部成立“質(zhì)量工程項(xiàng)目規(guī)劃工作組”,會(huì)同財(cái)政部開(kāi)展“質(zhì)量工程”前期調(diào)研、方案設(shè)計(jì)、經(jīng)費(fèi)測(cè)算和項(xiàng)目論證,上報(bào)國(guó)務(wù)院并得到批準(zhǔn)。歷史地看,“質(zhì)量工程”是高等教育從外延式擴(kuò)張向內(nèi)涵式發(fā)展轉(zhuǎn)型的產(chǎn)物,它自身也是推進(jìn)模式轉(zhuǎn)型的重要力量。
2. 項(xiàng)目設(shè)置從“研究型”轉(zhuǎn)向“建設(shè)型”。項(xiàng)目類型的轉(zhuǎn)向,標(biāo)志著“質(zhì)量工程”的性質(zhì)和內(nèi)容發(fā)生了深刻變化。“研究型”項(xiàng)目是問(wèn)題導(dǎo)向的,“建設(shè)型”項(xiàng)目是任務(wù)驅(qū)動(dòng)的,這都是由工程的性質(zhì)所決定的。其中,“教學(xué)內(nèi)容改革計(jì)劃”(1994~1999年)是典型的研究型,它在縱向上以“教學(xué)內(nèi)容和課程體系改革”為主題,橫向上以文、理、工、農(nóng)林、醫(yī)藥、經(jīng)濟(jì)和法學(xué)、師范等7個(gè)科類為載體,計(jì)劃項(xiàng)目類似于科研課題,研究成果多為論文、著作、教材;“新世紀(jì)教改工程”(2000~2003年)明顯具有過(guò)渡性,計(jì)劃中既有教改項(xiàng)目,又有研究課題;“高等學(xué)校教學(xué)質(zhì)量與教學(xué)改革工程”(2004~2006 年)項(xiàng)目分兩類,其中“精品課程”“優(yōu)秀教師”“大學(xué)英語(yǔ)”“教學(xué)評(píng)估”4個(gè)項(xiàng)目完全是“建設(shè)型”,而列入計(jì)劃未被啟動(dòng)的部分大多屬于應(yīng)用性研究課題。至2007年,“質(zhì)量工程”所確立的6個(gè)方面17個(gè)建設(shè)項(xiàng)目都屬于“建設(shè)型”。除“對(duì)口支援”項(xiàng)目外,其余都是針對(duì)本科教學(xué)的主要環(huán)節(jié)和主要方面設(shè)置的,非常接近于高等學(xué)校教學(xué)和管理工作的實(shí)際狀態(tài)。
3. 經(jīng)費(fèi)投入從部門(mén)自籌轉(zhuǎn)向中央財(cái)政專項(xiàng)支持。“教改工程”時(shí)期,項(xiàng)目經(jīng)費(fèi)一般是通過(guò)教育部籌集、相關(guān)部門(mén)資助、世行貸款、高校主管部門(mén)配套以及項(xiàng)目承擔(dān)高校補(bǔ)貼等途徑獲得的。“質(zhì)量工程”啟動(dòng)后,中央財(cái)政撥出25億元專項(xiàng)資金用于工程建設(shè),這是新中國(guó)成立以來(lái)中央財(cái)政用于高等教育教學(xué)質(zhì)量和人才培養(yǎng)方面的最大一筆專項(xiàng)投入。中央財(cái)政的大力支持,極大地激發(fā)了高校教學(xué)改革和質(zhì)量建設(shè)的積極性。據(jù)教育部公布的資料,“質(zhì)量工程”啟動(dòng)頭一年,就立項(xiàng)建設(shè)了818個(gè)“本科特色專業(yè)建設(shè)點(diǎn)”、2 467門(mén)“國(guó)家級(jí)精品課程”、400個(gè)“人才培養(yǎng)模式創(chuàng)新實(shí)驗(yàn)區(qū)”、360個(gè)“國(guó)家級(jí)實(shí)驗(yàn)教學(xué)示范中心”、6 135個(gè)“大學(xué)生創(chuàng)新性實(shí)驗(yàn)計(jì)劃項(xiàng)目”、400個(gè)“國(guó)家級(jí)教學(xué)團(tuán)隊(duì)”、400名“高等學(xué)校教學(xué)名師”、11 000多種基礎(chǔ)課程和專業(yè)課程教材、9個(gè)“大學(xué)生競(jìng)賽活動(dòng)資助項(xiàng)目”、200門(mén)“雙語(yǔ)教學(xué)示范課程”,1 000萬(wàn)大學(xué)生使用了“大學(xué)英語(yǔ)學(xué)習(xí)系統(tǒng)”。另外,還完成了“對(duì)口支援”項(xiàng)目中受援高校90個(gè)“數(shù)字化教室”的建設(shè),560名受援高校教師和120名教學(xué)管理干部到支援高校進(jìn)修和學(xué)習(xí)鍛煉[9]。如此浩大的教改工程,如果沒(méi)有中央財(cái)政的大力支持,是不可想象的。
(三)2011—2017年:“本科教學(xué)工程”時(shí)期
“本科教學(xué)工程”與“質(zhì)量工程”的全稱都是“高等學(xué)校本科教學(xué)質(zhì)量與教學(xué)改革工程”,從時(shí)序上看是“十二五”時(shí)期“質(zhì)量工程”的“二期實(shí)施方案”[10]。其實(shí),二者在改革內(nèi)容和管理方式有著重大變化。“本科教學(xué)工程”糾正了“質(zhì)量工程”時(shí)期的項(xiàng)目多而分散、經(jīng)費(fèi)支持力度小、申報(bào)審批程序繁雜等問(wèn)題,注重了項(xiàng)目的集成與創(chuàng)新及工程重點(diǎn)與核心的把握,突出了項(xiàng)目建設(shè)對(duì)人才培養(yǎng)的綜合效益。
1. 對(duì)“建設(shè)高等教育強(qiáng)國(guó)”目標(biāo)的呼應(yīng)。“建設(shè)高等教育強(qiáng)國(guó)”目標(biāo)的提出,是對(duì)黨的十七大“建設(shè)人力資源強(qiáng)國(guó)”論斷的回應(yīng)。時(shí)任國(guó)務(wù)委員陳至立在教育部直屬高校工作咨詢委員會(huì)第十八次全體會(huì)議上首次提出:“貫徹落實(shí)黨的十七大精神,建設(shè)人力資源強(qiáng)國(guó),就必須建設(shè)高等教育強(qiáng)國(guó)。”[11]2010年7月29日印發(fā)的《國(guó)家中長(zhǎng)期教育改革和發(fā)展規(guī)劃綱要(2010—2020年)》(簡(jiǎn)稱《綱要》)進(jìn)一步指出:“提高質(zhì)量是高等教育發(fā)展的核心任務(wù),是建設(shè)高等教育強(qiáng)國(guó)的基本要求。”為落實(shí)中央精神,教育部、財(cái)政部2011年7月1日印發(fā)《關(guān)于“十二五”期間實(shí)施“高等學(xué)校本科教學(xué)質(zhì)量與教學(xué)改革工程”的意見(jiàn)》(教高[2011]6號(hào)),明確指出:“我國(guó)教育事業(yè)已經(jīng)站在從教育大國(guó)向教育強(qiáng)國(guó)、從人力資源大國(guó)向人力資源強(qiáng)國(guó)邁進(jìn)的新的歷史起點(diǎn)上。高等教育作為科技第一生產(chǎn)力和人才第一資源的重要結(jié)合點(diǎn),在實(shí)現(xiàn)‘由大到強(qiáng)的轉(zhuǎn)變中起著十分重要的作用。”這一論述成了“本科教學(xué)工程”的出發(fā)點(diǎn)和落腳點(diǎn)。它所肩負(fù)的使命,就是提高高等教育質(zhì)量,推動(dòng)高等教育實(shí)現(xiàn)“由大到強(qiáng)”的根本轉(zhuǎn)變。
2. 教學(xué)改革和質(zhì)量建設(shè)“三級(jí)聯(lián)動(dòng)”體系的形成。“本科教學(xué)工程”采取分層管理,中央、地方、高校三級(jí)聯(lián)動(dòng)的體制,將部分項(xiàng)目逐步由中央向地方下移、由政府向高校轉(zhuǎn)移,實(shí)現(xiàn)了本科教學(xué)改革和質(zhì)量建設(shè)從立項(xiàng)管理向常態(tài)化建設(shè)的轉(zhuǎn)變。這一過(guò)程大致經(jīng)過(guò)了三個(gè)階段:(1)中央集中管理階段(2011~2013年)。教育部成立“本科教學(xué)工程”領(lǐng)導(dǎo)小組,決定工程的重大方針政策和總體規(guī)劃;領(lǐng)導(dǎo)小組下設(shè)辦公室,具體負(fù)責(zé)工程建設(shè)的日常工作,制訂、發(fā)布項(xiàng)目指南和規(guī)劃方案。各地教育主管 部門(mén)和項(xiàng)目承擔(dān)學(xué)校成立或指定專門(mén)機(jī)構(gòu),對(duì)口負(fù)責(zé)具體項(xiàng)目的規(guī)劃和實(shí)施。(2)過(guò)渡階段(2014— 2017年)。按照中央關(guān)于進(jìn)一步轉(zhuǎn)變部門(mén)管理職能的要求,“本科教學(xué)工程”管理方式由事前評(píng)審變?yōu)槭轮小⑹潞笤u(píng)估與監(jiān)管,高校在項(xiàng)目管理和實(shí)施中發(fā)揮著主體作用;項(xiàng)目?jī)?nèi)容除本科專業(yè)類教學(xué)質(zhì)量國(guó)家標(biāo)準(zhǔn)研制、國(guó)家級(jí)教師教學(xué)發(fā)展示范中心、國(guó)家級(jí)實(shí)驗(yàn)教學(xué)示范中心、西部受援高校教師和管理干部進(jìn)修鍛煉這4類仍由國(guó)家規(guī)劃安排外,其余項(xiàng)目均由高校自主安排;立項(xiàng)方式實(shí)現(xiàn)了從審批制到備案制的轉(zhuǎn)變,各高校擬定本校教學(xué)工程建設(shè)方案并報(bào)教育部備案,教育部綜合各校情況確定當(dāng)年經(jīng)費(fèi)額度,以“打包”整合的方式下達(dá)給高校,用于落實(shí)國(guó)家項(xiàng)目和學(xué)校自主安排的工程項(xiàng)目。(3)常態(tài)化建設(shè)階段(2017年之后)。教育部除發(fā)布和推行“國(guó)標(biāo)”之外,將主要力量集中在實(shí)施一流課程建設(shè)“雙萬(wàn)計(jì)劃”“六卓越一拔尖”人才培養(yǎng)計(jì)劃2.0版、專業(yè)質(zhì)量三級(jí)認(rèn)證與排名試點(diǎn)工作等項(xiàng)目上[13]。原“本科教學(xué)工程”中的項(xiàng)目設(shè)置與否、怎樣設(shè)置,純屬地方政府和高等學(xué)校的常規(guī)工作,意味著長(zhǎng)時(shí)間、大規(guī)模的教學(xué)改革和質(zhì)量建設(shè)方式已不適應(yīng)新時(shí)代的要求了。
3. “國(guó)標(biāo)”的研制對(duì)教育治理能力的提升。“本科教學(xué)工程”新增的“質(zhì)量標(biāo)準(zhǔn)建設(shè)”項(xiàng)目,其任務(wù)是組織研究制定覆蓋所有專業(yè)類的教學(xué)質(zhì)量國(guó)家標(biāo)準(zhǔn),推動(dòng)省級(jí)教育行政部門(mén)、行業(yè)組織和高校聯(lián)合制定相應(yīng)的專業(yè)教學(xué)質(zhì)量標(biāo)準(zhǔn),形成高等教育教學(xué)質(zhì)量標(biāo)準(zhǔn)體系。這個(gè)項(xiàng)目是教育部委托其下屬的專業(yè)類教學(xué)指導(dǎo)委員會(huì)(下文簡(jiǎn)稱“教指委”)完成的。項(xiàng)目啟動(dòng)于2013年,至2018年1月30日教育部召開(kāi)新聞發(fā)布會(huì)正式發(fā)布“普通高等學(xué)校本科專業(yè)類教學(xué)質(zhì)量國(guó)家標(biāo)準(zhǔn)”(簡(jiǎn)稱“國(guó)標(biāo)”),歷時(shí)5年之久。參與的專家教授達(dá)5 000多人,其中包括50多名兩院院士和知名專家。“國(guó)標(biāo)”涵蓋了普通高校本科專業(yè)目錄中全部92個(gè)本科專業(yè)類、587個(gè)專業(yè),涉及全國(guó)高校5.6萬(wàn)個(gè)專業(yè)點(diǎn)[14]。“國(guó)標(biāo)”文本內(nèi)容包括八個(gè)方面:概述、適用專業(yè)范圍、培養(yǎng)目標(biāo)、培養(yǎng)規(guī)格、師資隊(duì)伍、教學(xué)條件、質(zhì)量保障體系和附錄。與傳統(tǒng)教學(xué)規(guī)范相比,“國(guó)標(biāo)”最顯著的特點(diǎn)就是其靈活性。它既對(duì)各專業(yè)類提出了統(tǒng)一要求、保證基本質(zhì)量,又為各校各專業(yè)人才培養(yǎng)特色發(fā)展留出足夠的拓展空間;既對(duì)各專業(yè)類提出了教學(xué)基本要求,又對(duì)提升質(zhì)量提出前瞻性要求;既對(duì)各專業(yè)類標(biāo)準(zhǔn)提出定性要求,又包含必要的量化指標(biāo)[15]。“國(guó)標(biāo)”的發(fā)布,為各地各相關(guān)行業(yè)部門(mén)研制人才評(píng)價(jià)標(biāo)準(zhǔn)提供了依據(jù),也為高校修訂人才培養(yǎng)方案,培養(yǎng)多樣化、高質(zhì)量的人才提供了依據(jù),還為教育行政部門(mén)監(jiān)測(cè)認(rèn)證高校專業(yè)辦學(xué)質(zhì)量和水平提供了依據(jù),同時(shí)也為我國(guó)與其他國(guó)家開(kāi)展文憑互認(rèn)、學(xué)術(shù)交流提供了依據(jù),對(duì)促進(jìn)我國(guó)教育治理體系和治理能力現(xiàn)代化將發(fā)揮重要的基礎(chǔ)性作用。
二、對(duì)幾對(duì)矛盾關(guān)系的反思
“高等教育質(zhì)量工程”的建設(shè)史,也是我國(guó)高等教育由精英教育向大眾化教育轉(zhuǎn)型、由外延式發(fā)展向內(nèi)涵式發(fā)展轉(zhuǎn)型、由計(jì)劃管理向教育治理轉(zhuǎn)型的歷史。因此,不免要受來(lái)自各方面因素的影響和制約,它本身也是各種矛盾觀念的集合體。
(一)“效率”和“公平”的矛盾
試點(diǎn)先行、全面推廣,以點(diǎn)帶面、點(diǎn)面結(jié)合,是我國(guó)推行重大政策時(shí)常用的方法。教改工程立項(xiàng)說(shuō)到底是辦學(xué)資源尤其是政策資源的重新分配,而資源的稀缺性決定了效率與公平的矛盾是不可避免的。為調(diào)和矛盾,“高等教育質(zhì)量工程”采取了三項(xiàng)措施:(1)利用現(xiàn)代信息技術(shù),實(shí)現(xiàn)“國(guó)家級(jí)精品課程”資源共享。“十五”期間,教育部建成了1 139門(mén)國(guó)家級(jí)精品課程,“十一五”時(shí)期又安排了3 000門(mén)課程予以重點(diǎn)建設(shè)。為使這4 000多門(mén)國(guó)家精品課程發(fā)揮更大效益,教育部啟動(dòng)“國(guó)家精品課程集成”項(xiàng)目,建成國(guó)家精品課程資源中心,為公眾提供課程內(nèi)容快速訪問(wèn)和個(gè)性化主動(dòng)學(xué)習(xí)等服務(wù)。2011年,教育部啟動(dòng)“國(guó)家精品開(kāi)放課程建設(shè)與共享”項(xiàng)目,建設(shè)1 000門(mén)精品視頻公開(kāi)課和5 000門(mén)國(guó)家級(jí)精品資源共享課,并在其中遴選出400門(mén)國(guó)家級(jí)網(wǎng)絡(luò)教育精品資源共享課,通過(guò)網(wǎng)絡(luò)途徑促進(jìn)傳播和共享。(2)建立代償機(jī)制,縮小地區(qū)差距。2007年,國(guó)家將“對(duì)口支援”項(xiàng)目納入“高等教育質(zhì)量工程”,投入5.1億元,每年資助受援高校的一批教師和教學(xué)管理干部到支援高校進(jìn)修和學(xué)習(xí)鍛煉,并為受援高校建設(shè)一批數(shù)字化教室。(3)推出“高等教育質(zhì)量工程”配套政策。1994年6月,原國(guó)家教委首次提出的“教學(xué)內(nèi)容改革計(jì)劃”,就是其印發(fā)的《關(guān)于加強(qiáng)普通高等學(xué)校教學(xué)工作的意見(jiàn)》(教高[1994]10號(hào))的一項(xiàng)具體措施;2000年1月,教育部推出“新世紀(jì)教改工程”,并于次年8月印發(fā)了《關(guān)于加強(qiáng)高等學(xué)校本科教學(xué)工作提高教學(xué)質(zhì)量的若干意見(jiàn)》(教高[2001]4號(hào))與之相配套;2004年2月起,實(shí)施“高等學(xué)校教學(xué)質(zhì)量與教學(xué)改革工程”,次年1月又印發(fā)了配套文件《關(guān)于進(jìn)一步加強(qiáng)高等學(xué)校本科教學(xué)工作的若干意見(jiàn)》(教高[2005]1號(hào));2007年1月教育部、財(cái)政部聯(lián)合推出“質(zhì)量工程”,教育部隨即于同年2月印發(fā)了《關(guān)于進(jìn)一步深化本科教學(xué)改革 全面提高教學(xué)質(zhì)量的若干意見(jiàn)》(教高[2007]2號(hào));教育部、財(cái)政部在2011年7月推出“本科教學(xué)工程”,教育部便于次年3月印發(fā)了《關(guān)于全面提高高等教育質(zhì)量的若干意見(jiàn)》(教高[2012]4號(hào))。這種政策配套方式看似很完美,其實(shí)二者是“兩張皮”。原因在于它們一個(gè)務(wù)實(shí)、一個(gè)務(wù)虛;一個(gè)真金白銀、一個(gè)鏡花水月,一經(jīng)實(shí)施便成了“夾生飯”。至于“對(duì)口支援”項(xiàng)目,顯然重在物質(zhì)補(bǔ)償而非能力提高,是“授人以魚(yú)”而非“授人以漁”,其結(jié)果必然是強(qiáng)者恒強(qiáng)、弱者恒弱,原有差距不但沒(méi)有縮小,反而擴(kuò)大了。
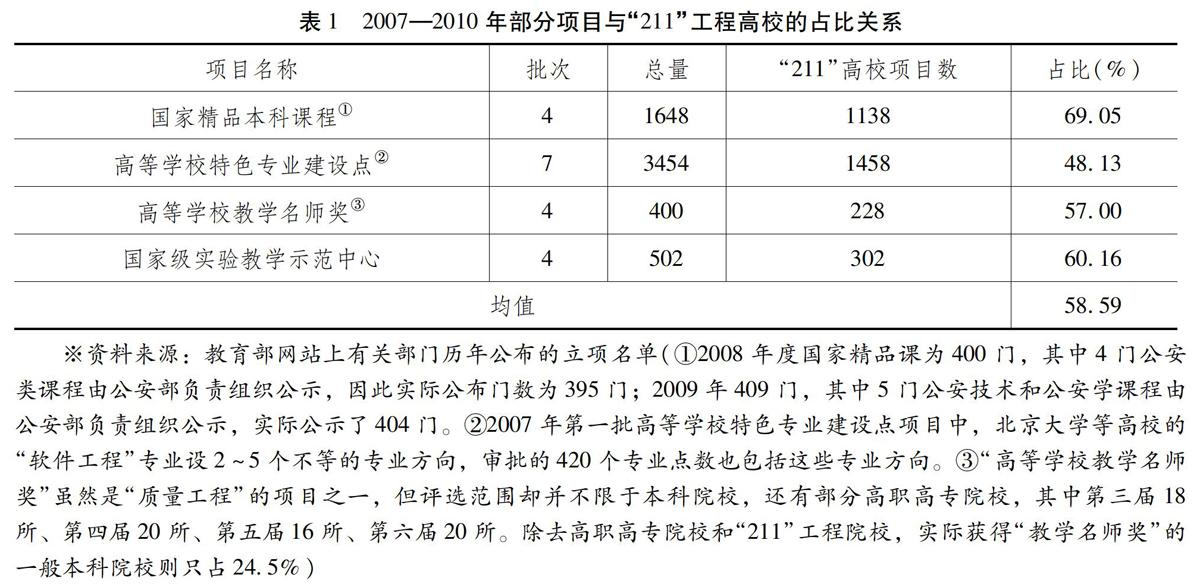
在競(jìng)爭(zhēng)條件下,公平與效率永遠(yuǎn)都是對(duì)立的矛盾。正如《新約·馬太福音》里所說(shuō)的那樣:“凡有的,還要加給他,叫他有余。沒(méi)有的,連他所有的,也要奪過(guò)來(lái)。”“高等教育質(zhì)量工程”的“馬太效應(yīng)”是怎樣形成的?這與其立項(xiàng)機(jī)制設(shè)計(jì)中突出激勵(lì)性、競(jìng)爭(zhēng)性因素有關(guān)。表現(xiàn)在:國(guó)家規(guī)定項(xiàng)目建設(shè)目標(biāo)及立項(xiàng)標(biāo)準(zhǔn),并從申報(bào)高校中以差額或小概率方式遴選出立項(xiàng)者,給予它們相應(yīng)的榮譽(yù)稱號(hào)和資金支持;高校以國(guó)家公布的遴選標(biāo)準(zhǔn)聚集、調(diào)動(dòng)、培育競(jìng)爭(zhēng)優(yōu)勢(shì)以爭(zhēng)取國(guó)家項(xiàng)目,并將獲得的項(xiàng)目轉(zhuǎn)換成提高水平、增進(jìn)聲譽(yù)的辦學(xué)資源,從而形成新的競(jìng)爭(zhēng)優(yōu)勢(shì)。這種以競(jìng)爭(zhēng)為杠桿的機(jī)制設(shè)計(jì),其結(jié)果必然是先入為主、贏者通吃。這一點(diǎn)可以通過(guò)對(duì)項(xiàng)目去向的簡(jiǎn)單統(tǒng)計(jì)就可以得到證明。2011年,我國(guó)有普通本科高校820所。設(shè)其中112所“211”工程院校為立項(xiàng)競(jìng)爭(zhēng)的一方,其余708所一般本科院校為另一方,并以2007—2010年期間“精品課程”“特色專業(yè)”“教學(xué)名師”“示范中心”這4個(gè)項(xiàng)目為指標(biāo),可以得到雙方立項(xiàng)情況的統(tǒng)計(jì)結(jié)果(表1)。
由表1可以看出,“質(zhì)量工程”多數(shù)項(xiàng)目落入“211”工程院校。“211”工程院校僅占我國(guó)本科院校總數(shù)的13.66%,卻收獲了近六成的項(xiàng)目,其傾向性是顯而易見(jiàn)的;再考慮到“211”工程院校主要集中在北京(26所)、江蘇(11所)、上海(9所)、陜西(8所)、湖北(7所)等傳統(tǒng)高等教育強(qiáng)省,這些省份因此而獲得了相對(duì)較多的項(xiàng)目;如若加上經(jīng)國(guó)家批準(zhǔn)設(shè)立的311所獨(dú)立學(xué)院和國(guó)家審定的70個(gè)分校辦學(xué)點(diǎn)(即“成人高校”),“質(zhì)量工程”項(xiàng)目的集中度還要大幅度提高。這種以效率為指向的非均衡發(fā)展策略,必然是以犧牲多數(shù)地區(qū)、多數(shù)學(xué)校和多數(shù)學(xué)生的切身利益為代價(jià)的,因此是不可持續(xù)的。
(二)“項(xiàng)目化”管理與常規(guī)管理的矛盾
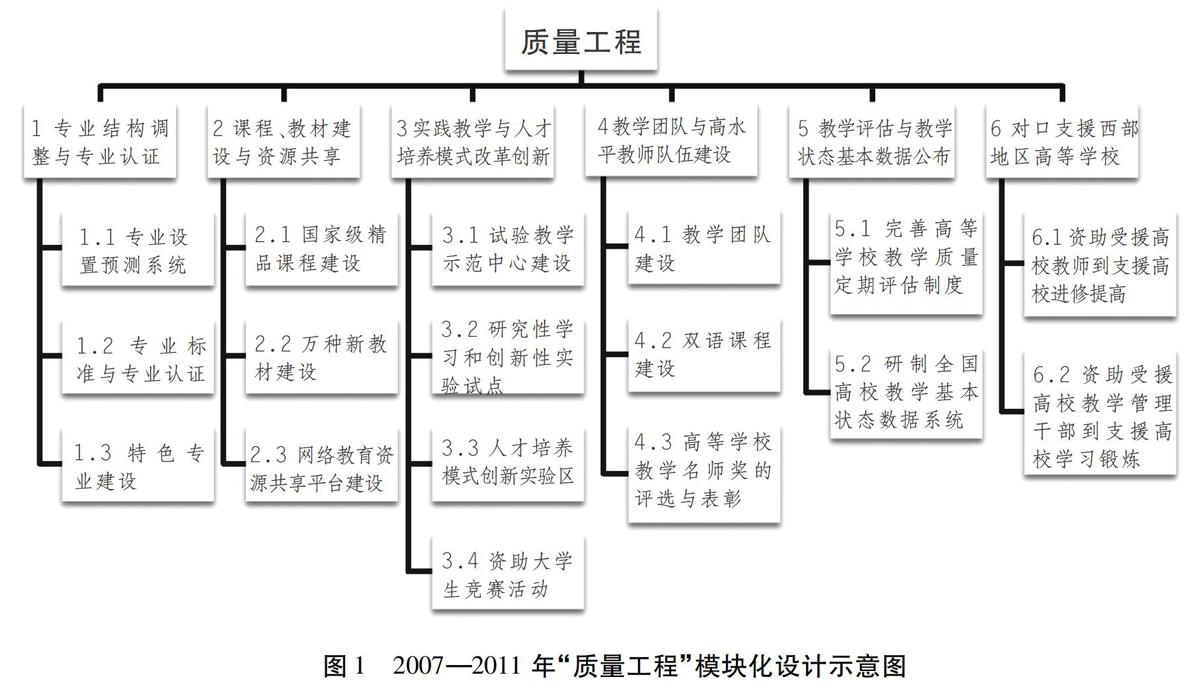
“項(xiàng)目化”是由美國(guó)IBM公司(國(guó)際商業(yè)機(jī)器公司)于1996年首創(chuàng)的組織管理方式,是一種利用項(xiàng)目打包技術(shù),將一項(xiàng)工作整齊地切割成項(xiàng)目,然后實(shí)施量化管理的方法。這種方法一經(jīng)問(wèn)世便風(fēng)行全球,在我國(guó)經(jīng)濟(jì)建設(shè)和社會(huì)管理的不少部門(mén)都得到了運(yùn)用。“項(xiàng)目化”管理與常規(guī)管理相比有許多明顯優(yōu)勢(shì),這在“質(zhì)量工程”實(shí)施中表現(xiàn)得尤為突出。(1)精細(xì)化施工。“質(zhì)量工程”各項(xiàng)目的申報(bào)立項(xiàng)、檢查驗(yàn)收,專項(xiàng)資金的預(yù)算、支出、決算,以及經(jīng)費(fèi)執(zhí)行的監(jiān)督檢查與績(jī)效考評(píng)等,都是在教育部和財(cái)政部聯(lián)合成立的質(zhì)量工程領(lǐng)導(dǎo)小組領(lǐng)導(dǎo)下,由教育部高教司具體推動(dòng)的。工程建設(shè)中每個(gè)項(xiàng)目、各項(xiàng)目的每個(gè)實(shí)施環(huán)節(jié),都有具體而詳細(xì)的要求和規(guī)定。據(jù)不完全統(tǒng)計(jì),從2007年1月至2011年7月,共印發(fā)“質(zhì)量工程”專項(xiàng)文件120件,其中由教育部、財(cái)政部聯(lián)署文件就達(dá)50份,占總數(shù)的40%以上。(2)模塊化設(shè)計(jì)。“質(zhì)量工程”規(guī)劃了6類建設(shè)項(xiàng)目,代表了高校教學(xué)工作的6個(gè)主要環(huán)節(jié);每個(gè)類型又由若干具體項(xiàng)目構(gòu)成,這些具體項(xiàng)目就是“質(zhì)量工程”的功能模塊(圖1)。從上而下,它是一個(gè)可分解的系統(tǒng),每一個(gè)可執(zhí)行的功能模塊都是可以單獨(dú)立項(xiàng)、驗(yàn)收的,其中任何一個(gè)項(xiàng)目出現(xiàn)問(wèn)題,都不會(huì)影響“質(zhì)量工程”的總體運(yùn)行;從下而上,這些模塊又可以組合起來(lái)形成若干子系統(tǒng),這些子系統(tǒng)組合起來(lái)就是“質(zhì)量工程”系統(tǒng)。(3)扁平化管理。傳統(tǒng)上,教學(xué)改革和質(zhì)量建設(shè)是高等學(xué)校的基本職能。它縱向設(shè)置學(xué)部、學(xué)院、學(xué)系、教研室等教學(xué)機(jī)構(gòu),具體組織教學(xué)工作;橫向設(shè)置教務(wù)處,統(tǒng)籌管理學(xué)科專業(yè)建設(shè)、教學(xué)計(jì)劃制訂、課程教學(xué)組織、教材建設(shè)供應(yīng)、實(shí)驗(yàn)實(shí)習(xí)實(shí)訓(xùn)管理、教學(xué)改革與研究等活動(dòng)。“質(zhì)量工程”的實(shí)施,使得教育部有機(jī)會(huì)直接介入高校教學(xué)管理工作,使國(guó)家宏觀政策與高校教學(xué)教改和質(zhì)量建設(shè)目標(biāo)相對(duì)接,從而減少了管理層次,降低了政策信息損失,從而提高了“質(zhì)量工程”的實(shí)施效率。當(dāng)然,這種管理不是“接管”或“代管”,也不是與高校“共管”,而是通過(guò)制定標(biāo)準(zhǔn)、項(xiàng)目培訓(xùn)、學(xué)術(shù)研討、委托管理、成果驗(yàn)收、經(jīng)費(fèi)投入等方式影響高校的教學(xué)過(guò)程;管理的力量也不是通過(guò)科層組織垂直傳遞的,而是以項(xiàng)目管理方式嵌入高校教學(xué)過(guò)程,從而對(duì)高校教學(xué)改革和質(zhì)量建設(shè)工作施加影響的。
目前,“高等教育質(zhì)量工程”已告完工,高校教學(xué)改革和質(zhì)量建設(shè)工作也將進(jìn)入常態(tài)化。對(duì)此,有兩種新情況需要高校去面對(duì):一是如何確保“高等教育質(zhì)量工程”成果的長(zhǎng)效性。提高教育質(zhì)量是一個(gè)長(zhǎng)期的過(guò)程,絕不可能依靠幾次“會(huì)戰(zhàn)”、實(shí)施幾項(xiàng)“工程”就能畢其功于一役。能否長(zhǎng)久保持對(duì)教學(xué)改革的熱情,長(zhǎng)久專注于高等教育質(zhì)量的提升,是對(duì)每一位高教工作者的嚴(yán)肅考驗(yàn)。二是如何為高校教學(xué)改革注入新的活力。“高等教育質(zhì)量工程”之所以受到高等學(xué)校的歡迎,不僅在于其改革主題的重要性,更在于其項(xiàng)目管理的激勵(lì)性。在生源、師資、資金等辦學(xué)市場(chǎng)發(fā)育并不完善的條件下,政策資源往往是高校競(jìng)爭(zhēng)的主要內(nèi)容。因此,與其說(shuō)“高等教育質(zhì)量工程”是教學(xué)改革的全國(guó)“大會(huì)戰(zhàn)”,毋寧說(shuō)是一場(chǎng)高等學(xué)校的“造星運(yùn)動(dòng)”。如何讓國(guó)家投入的這部分稀缺資源繼續(xù)發(fā)揮應(yīng)有作用,不使其成色隨著工程建設(shè)的結(jié)束而逐漸流失,是需要高校辦學(xué)者認(rèn)真思考的問(wèn)題。
(三)“最好的教育”與“適合的教育”的矛盾
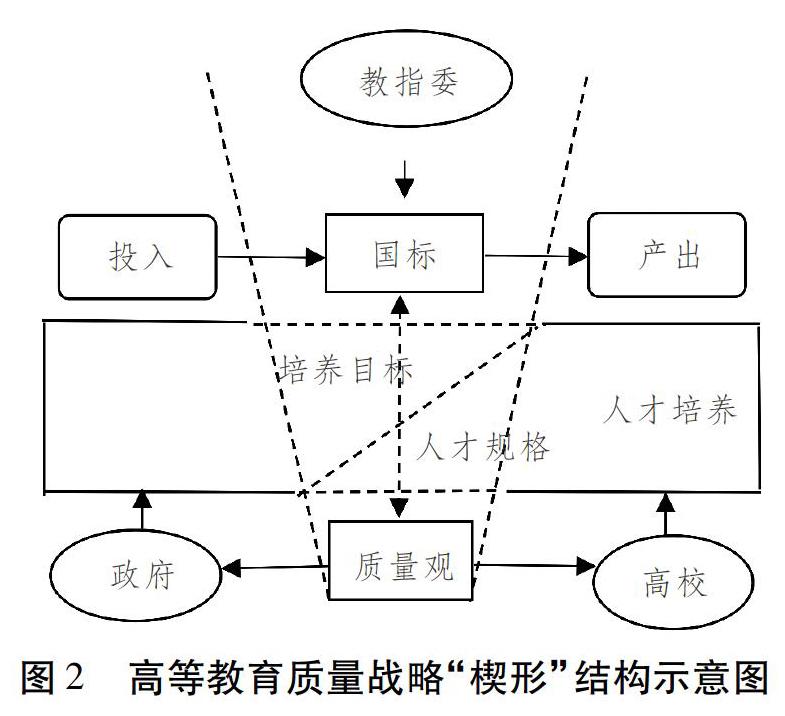
教學(xué)改革和質(zhì)量建設(shè)的終極目標(biāo),就是創(chuàng)造“最好的教育”。那么,什么是“最好的教育”?這要從“高等教育質(zhì)量工程”所秉持的質(zhì)量觀中去考察。分析可知,“高等教育質(zhì)量工程”的設(shè)計(jì)理念蘊(yùn)含了兩種思維方式:一是“極致化”思維。其項(xiàng)目是通過(guò)層層評(píng)審遴選出來(lái)的,“國(guó)家級(jí)項(xiàng)目”以“省級(jí)項(xiàng)目”為基礎(chǔ),“省級(jí)項(xiàng)目”以“校級(jí)項(xiàng)目”為基礎(chǔ),而“校級(jí)項(xiàng)目”又是從大量未獲立項(xiàng)的項(xiàng)目中遴選出來(lái)的,從而形成“三級(jí)聯(lián)動(dòng)”的“金字塔”結(jié)構(gòu),處于塔尖的國(guó)家級(jí)項(xiàng)目自然代表了我國(guó)教學(xué)工作的最高水平。二是“底線”思維。質(zhì)量提升是一個(gè)起伏的過(guò)程,既有上升勢(shì)頭,也必然存在下滑的潛勢(shì)。為此,“高等教育質(zhì)量工程”中還有部分“保底”項(xiàng)目。它們不是遴選出來(lái)的,而是由教育部委托有關(guān)方面完成的。比如,2013年教育部委托“教指委”完成的“普通高等學(xué)校本科專業(yè)類教學(xué)質(zhì)量國(guó)家標(biāo)準(zhǔn)”,就是面向全部高校、全部在校生制定的。在“國(guó)標(biāo)”設(shè)計(jì)者的頭腦中,高等學(xué)校教學(xué)工作是在一個(gè)上有標(biāo)桿、下有底線的框架內(nèi)有序運(yùn)行的,因此教育質(zhì)量是總體可控的。當(dāng)然,這只是一種應(yīng)然狀態(tài),效果如何還須用實(shí)踐來(lái)檢驗(yàn)。客觀的說(shuō),“高等教育質(zhì)量工程”對(duì)鞏固高校教學(xué)工作的中心地位、推動(dòng)高校加大教學(xué)基礎(chǔ)建設(shè)投入,確實(shí)發(fā)揮了重要作用。但是還應(yīng)該看到,當(dāng)前公眾對(duì)于高等教育質(zhì)量的滿意度并不高。中國(guó)教育科學(xué)研究院2016年開(kāi)展的一項(xiàng)調(diào)查顯示,社會(huì)各界對(duì)我國(guó)高等教育的總體滿意度指數(shù)為69.42分,其中教育質(zhì)量的滿意度指數(shù)僅為67.87分[16]。盡管這不是針對(duì)“高等教育質(zhì)量工程”所做的專項(xiàng)調(diào)查,但既然國(guó)家耗費(fèi)了巨大的人力、財(cái)力、精力專門(mén)解決高等教育質(zhì)量問(wèn)題,就不能說(shuō)調(diào)查結(jié)果與“高等教育質(zhì)量工程”毫無(wú)關(guān)系。
既然如此,為什么公眾“無(wú)感”于“高等教育質(zhì)量工程”的成績(jī)呢?或許只能用“質(zhì)量觀”的不同來(lái)解釋。傳統(tǒng)上,高等教育是以班級(jí)授課制為基礎(chǔ)的,它追求的是人才培養(yǎng)的規(guī)模化、專門(mén)化和標(biāo)準(zhǔn)化。從這個(gè)角度講,“高等教育質(zhì)量工程”是成功的。但“成功的”并不意味著是“最好的”,只有“適合的”才是“最好的”。當(dāng)前,我國(guó)正處在工業(yè)化中后期,部分地區(qū)和行業(yè)已開(kāi)始向后工業(yè)化社會(huì)邁進(jìn),個(gè)性化生產(chǎn)已成為財(cái)富增長(zhǎng)最快的領(lǐng)域之一。反映在高等教育上,其質(zhì)量標(biāo)準(zhǔn)不僅要適合于國(guó)家需要,也要適合于高校的層次和類型,還要適合于學(xué)生多樣化、個(gè)性化發(fā)展的需求。《綱要》指出:“關(guān)心每個(gè)學(xué)生,促進(jìn)每個(gè)學(xué)生主動(dòng)地、生動(dòng)活潑地發(fā)展,尊重教育規(guī)律和學(xué)生身心發(fā)展規(guī)律,為每個(gè)學(xué)生提供適合的教育。”這是當(dāng)前為高校教學(xué)改革和質(zhì)量建設(shè)提出的新要求。如果仍然信守那種批量化、標(biāo)準(zhǔn)化的教育方式而不思改變,那么資源和精力投入得越多、工作做得越扎實(shí)充分,就會(huì)與真正的高質(zhì)量教育離得越遠(yuǎn)。
三、對(duì)推動(dòng)“國(guó)標(biāo)”再標(biāo)準(zhǔn)化的思考
“國(guó)標(biāo)”的研制與發(fā)布,是“高等教育質(zhì)量工程”的一大亮點(diǎn)。但如果將其與國(guó)家標(biāo)準(zhǔn)化工作的規(guī)范來(lái)要求,會(huì)發(fā)現(xiàn)還有相當(dāng)大的差距。當(dāng)前,首要任務(wù)是推動(dòng)“國(guó)標(biāo)”在原有基礎(chǔ)上的“再標(biāo)準(zhǔn)化”,具體說(shuō)就是實(shí)現(xiàn)“國(guó)標(biāo)”制定的規(guī)范化、“國(guó)標(biāo)”制定者“教指委”的合法化、以及政府在高校教學(xué)改革和質(zhì)量建設(shè)中定位的合理化。
(一)為“國(guó)標(biāo)”正名
古人云:名不正則言不順,言不順則事不成。“普通高等學(xué)校本科專業(yè)類教學(xué)質(zhì)量國(guó)家標(biāo)準(zhǔn)”以“國(guó)家標(biāo)準(zhǔn)”命名,實(shí)際是對(duì)“標(biāo)準(zhǔn)”一詞的誤用;而媒體和部分官方文件將其簡(jiǎn)稱為“國(guó)標(biāo)”,更是錯(cuò)上加錯(cuò)。國(guó)家標(biāo)準(zhǔn)GB/T 3935.1—83對(duì)“標(biāo)準(zhǔn)”一詞的定義是:“標(biāo)準(zhǔn)是對(duì)重復(fù)性事物和概念所做的統(tǒng)一規(guī)定,它以科學(xué)、技術(shù)和實(shí)踐經(jīng)驗(yàn)的綜合為基礎(chǔ),經(jīng)過(guò)有關(guān)方面協(xié)商一致,由主管機(jī)構(gòu)批準(zhǔn),以特定的形式發(fā)布,作為共同遵守的準(zhǔn)則和依據(jù)。”在這里,“標(biāo)準(zhǔn)”除了其內(nèi)涵須符合要求外,“主管機(jī)構(gòu)批準(zhǔn)”和“特定形式發(fā)布”是必要條件。因此,判斷“國(guó)標(biāo)”是不是標(biāo)準(zhǔn)化意義上的“標(biāo)準(zhǔn)”,只要看看是否獲得了有關(guān)部門(mén)的批準(zhǔn)就能明了。標(biāo)準(zhǔn)分國(guó)家標(biāo)準(zhǔn)、行業(yè)標(biāo)準(zhǔn)、地方標(biāo)準(zhǔn)和團(tuán)體標(biāo)準(zhǔn)、企業(yè)標(biāo)準(zhǔn)。據(jù)此,我們逐項(xiàng)檢索相關(guān)數(shù)據(jù)庫(kù),并得出如下結(jié)論:(1)“國(guó)標(biāo)”不是“國(guó)家標(biāo)準(zhǔn)”。“國(guó)家標(biāo)準(zhǔn)”分為“強(qiáng)制性國(guó)家標(biāo)準(zhǔn)”和“推薦性國(guó)家標(biāo)準(zhǔn)”。其中,“國(guó)家標(biāo)準(zhǔn)全文公開(kāi)系統(tǒng)” [17]收錄“強(qiáng)制性國(guó)家標(biāo)準(zhǔn)”1 967條,但尚未收錄任何教育類標(biāo)準(zhǔn);收錄“推薦性國(guó)家標(biāo)準(zhǔn)”33 043條,其中教育類44條,但不包括“國(guó)標(biāo)”在內(nèi)。(2)“國(guó)標(biāo)”也不是“行業(yè)標(biāo)準(zhǔn)”。檢索“全國(guó)標(biāo)準(zhǔn)信息公共服務(wù)平臺(tái)”[18],其中收錄了教育類行業(yè)標(biāo)準(zhǔn)(分類代碼:JY)221件,沒(méi)有“國(guó)標(biāo)”在內(nèi)。(3)“國(guó)標(biāo)”也不是“團(tuán)體標(biāo)準(zhǔn)”。“全國(guó)團(tuán)體標(biāo)準(zhǔn)信息平臺(tái)”[19]共收錄教育類團(tuán)體標(biāo)準(zhǔn)(分類代碼:P)42條,但沒(méi)有一條是“國(guó)標(biāo)”。至于“地方標(biāo)準(zhǔn)”和“企業(yè)標(biāo)準(zhǔn)”,因與“國(guó)標(biāo)”發(fā)布者和制定者身份不符,可直接排除在外。綜上可以看出,教育部發(fā)布的“國(guó)標(biāo)”并未獲得國(guó)家標(biāo)準(zhǔn)委員會(huì)的批準(zhǔn)或備案,這種所謂的“標(biāo)準(zhǔn)”缺乏最起碼的規(guī)范性、通用性要求,既不受國(guó)家標(biāo)準(zhǔn)化法律法規(guī)的約束,也無(wú)法獲得國(guó)家標(biāo)準(zhǔn)化管理機(jī)構(gòu)的支持,因此它在許多場(chǎng)合是不被承認(rèn)的。
教育標(biāo)準(zhǔn)是國(guó)家重要的教育制度之一,是一種根本性的教育規(guī)范[20]。而要使“國(guó)標(biāo)”成為高校教學(xué)工作的依據(jù)、教育部門(mén)執(zhí)法監(jiān)管的依據(jù)、受教育者維權(quán)的依據(jù)、國(guó)際社會(huì)互相交流的依據(jù),當(dāng)務(wù)之急是實(shí)現(xiàn)“國(guó)標(biāo)”制定工作的規(guī)范化,將“國(guó)標(biāo)”納入國(guó)家標(biāo)準(zhǔn)化工作體系中統(tǒng)籌管理。至于能否將“國(guó)標(biāo)”界定為“國(guó)家標(biāo)準(zhǔn)”,則要根據(jù)其功能和范圍來(lái)確定。國(guó)家給標(biāo)準(zhǔn)劃分位階,是要各類標(biāo)準(zhǔn)根據(jù)自身功能和適用范圍各安其位,從而形成強(qiáng)制性標(biāo)準(zhǔn)“守底線”、推薦性標(biāo)準(zhǔn)“保基本”、行業(yè)標(biāo)準(zhǔn)“補(bǔ)遺漏”、團(tuán)體標(biāo)準(zhǔn)“搞創(chuàng)新”、企業(yè)標(biāo)準(zhǔn)“強(qiáng)質(zhì)量”的格局[21]。對(duì)此,有學(xué)者認(rèn)為教育標(biāo)準(zhǔn)應(yīng)盡可能以“國(guó)家標(biāo)準(zhǔn)”的形式頒布,“通常情況下至少應(yīng)由國(guó)務(wù)院頒布教育標(biāo)準(zhǔn),以確保國(guó)家教育標(biāo)準(zhǔn)的權(quán)威性、強(qiáng)制性和執(zhí)行力”[22]。但這既不現(xiàn)實(shí),也不必要。《標(biāo)準(zhǔn)法》規(guī)定:“強(qiáng)制性國(guó)家標(biāo)準(zhǔn)”(分類代碼:GB)是對(duì)保障人身健康和生命財(cái)產(chǎn)安全、國(guó)家安全、生態(tài)環(huán)境安全以及滿足經(jīng)濟(jì)社會(huì)管理基本需要的技術(shù)要求;“推薦性國(guó)家標(biāo)準(zhǔn)”(分類代碼:GB/T)是滿足基礎(chǔ)通用、與強(qiáng)制性國(guó)家標(biāo)準(zhǔn)配套、對(duì)各有關(guān)行業(yè)起引領(lǐng)作用等需要的技術(shù)要求。而教育部發(fā)布的“國(guó)標(biāo)”只是對(duì)高校教學(xué)工作的質(zhì)量要求,既無(wú)渉安全問(wèn)題,也算不上“基礎(chǔ)通用”,因此不可能列入國(guó)家標(biāo)準(zhǔn)。另外,排除“地方標(biāo)準(zhǔn)”和“企業(yè)標(biāo)準(zhǔn)”,在剩余的“行業(yè)標(biāo)準(zhǔn)”和“團(tuán)體標(biāo)準(zhǔn)”中,筆者傾向于用“團(tuán)體標(biāo)準(zhǔn)”來(lái)界定“國(guó)標(biāo)”的屬性。理由是:第一,“行業(yè)標(biāo)準(zhǔn)”是對(duì)沒(méi)有國(guó)家標(biāo)準(zhǔn)而又需要在全國(guó)某個(gè)行業(yè)范圍內(nèi)統(tǒng)一技術(shù)要求所制定的標(biāo)準(zhǔn),它與“國(guó)家標(biāo)準(zhǔn)”的區(qū)別只在于范圍和等級(jí)不同,其內(nèi)涵是相同或相似的,本身也包括強(qiáng)制性標(biāo)準(zhǔn)和推薦性標(biāo)準(zhǔn),這與“國(guó)標(biāo)”的性質(zhì)不符。第二,“團(tuán)體標(biāo)準(zhǔn)”是《標(biāo)準(zhǔn)法》修訂后為適應(yīng)市場(chǎng)經(jīng)濟(jì)而新增加的類型,也是國(guó)家鼓勵(lì)使用的類型。與其他標(biāo)準(zhǔn)相比,其特點(diǎn)是“三自”:團(tuán)體自己確立制定程序,自主制定、發(fā)布、采納,社會(huì)自愿采用。如是觀之,“國(guó)標(biāo)”與團(tuán)體標(biāo)準(zhǔn)的“三自”特點(diǎn)有很多相通之處:“國(guó)標(biāo)”既有“規(guī)矩”又有“空間”,既有“底線”又有“目標(biāo)”,既有“定性”又有“定量”[23],是一個(gè)富有彈性的質(zhì)量標(biāo)準(zhǔn)。將“國(guó)標(biāo)”歸類于“團(tuán)體標(biāo)準(zhǔn)”,也與落實(shí)高校辦學(xué)自主權(quán)的原則是一致的。這是因?yàn)椋俸谩⒃偻昝赖臉?biāo)準(zhǔn)也不可能代替高校的教學(xué)工作。《高等教育法》明確規(guī)定:高等學(xué)校根據(jù)教學(xué)需要,自主制定教學(xué)計(jì)劃、選編教材、組織實(shí)施教學(xué)活動(dòng)。那種強(qiáng)制要求全國(guó)高校使用統(tǒng)一標(biāo)準(zhǔn)、統(tǒng)一計(jì)劃、統(tǒng)一教材來(lái)組織教學(xué)的時(shí)代早就一去不復(fù)返了。第三,“團(tuán)體標(biāo)準(zhǔn)”是在行業(yè)行政主管部門(mén)指導(dǎo)下,由具有法人資質(zhì),且具備相應(yīng)專業(yè)和標(biāo)準(zhǔn)化能力的學(xué)會(huì)、協(xié)會(huì)、商會(huì)、聯(lián)合會(huì)等社會(huì)組織和產(chǎn)業(yè)技術(shù)聯(lián)盟(即所謂“社會(huì)團(tuán)體”),經(jīng)過(guò)公開(kāi)、透明、協(xié)商一致原則制定,并能夠共同使用和重復(fù)使用的規(guī)范性文件。以此律之,“教指委”還需要取得法人資質(zhì),才會(huì)擁有資格制定具有“團(tuán)體標(biāo)準(zhǔn)”屬性的教學(xué)質(zhì)量標(biāo)準(zhǔn)。
參考文獻(xiàn):
[1]孫緯君,陳浩.突出教學(xué)主旋律推動(dòng)質(zhì)量上臺(tái)階——國(guó)家教委高教司周遠(yuǎn)清司長(zhǎng)訪談錄[J].中國(guó)高等教育,1993(Z1).
[2]陳浩,徐越.教學(xué)要升溫 教學(xué)要再加溫——國(guó)家教委高教司周遠(yuǎn)清司長(zhǎng)訪談錄[J].中國(guó)高等教育,1995(1).
[3]黎琳.“高等教育面向21世紀(jì)教學(xué)內(nèi)容和課程體系改革計(jì)劃”述評(píng)[J].高等理科教育,2001(02).
[4]趙卿敏.實(shí)施“面向21世紀(jì)教學(xué)內(nèi)容和課程體系改革計(jì)劃”的回顧與思考[J].中國(guó)大學(xué)教學(xué),2000(03).
[5]李嵐清.2002年5月10日在第四屆高等教育國(guó)家級(jí)教學(xué)成果獎(jiǎng)暨第三屆教育部高校青年教師獎(jiǎng)?lì)C獎(jiǎng)大會(huì)上的講話[EB/OL].教育部網(wǎng)站,http://www.moe.gov.cn/jyb_xxgk/gk_gbgg/moe_0/moe_8/moe_26/tnull_368.html.
[6]高等學(xué)校教學(xué)質(zhì)量工程啟動(dòng)——評(píng)選精品課程 嘉獎(jiǎng)教學(xué)名師 改革英語(yǔ)教學(xué) 建立評(píng)估制度[N].人民日?qǐng)?bào),2003-4-10.
[7]全面提高人才培養(yǎng)質(zhì)量 教育部實(shí)施高教“質(zhì)量工程”[N].人民日?qǐng)?bào)(海外版),2003-04-11(2).
[8]胡錦濤強(qiáng)調(diào)努力辦好讓人民群眾滿意的教育[EB/OL].http://www.huaxia.com/xw/zdxw/gcdt/2006/00503490.html.
[9]提高高等教育質(zhì)量[EB/OL].教育部網(wǎng)站,http://www.moe.gov.cn/jyb_xwfb/xw_fbh/moe_2606/moe_2074/moe_2438/moe_2442/tnull_39567.html.
[10]高教司司長(zhǎng)張大良:改革創(chuàng)新推動(dòng)高等教育發(fā)展[EB/OL].教育部網(wǎng)站,http://www.moe.gov.cn/s78/A08/gjs_left/s5174/s5176/201103/t20110329_116341.html.
[11]陳至立.認(rèn)真學(xué)習(xí)貫徹黨的十七大精神 以提高質(zhì)量為核心 加快從高等教育大國(guó)向高等教育強(qiáng)國(guó)邁進(jìn)的步伐——在教育部直屬高校工作咨詢委員會(huì)第十八次全體會(huì)議上的講話[EB/OL]. http://www.moe.gov.cn/srcsite/A14/A14_other/200712/t20071222_75412.html.
[12][13][14][15][23]吳巖.《普通高等學(xué)校本科專業(yè)類教學(xué)質(zhì)量國(guó)家標(biāo)準(zhǔn)》有關(guān)情況介紹[EB/OL].教育部網(wǎng)站,http://www.moe.gov.cn/jyb_xwfb/xw_fbh/moe_2069/xwfbh_2018n/xwfb_20180130/sfcl/201801/t20180130_325921.html.
[16]中國(guó)教育科學(xué)研究院.全國(guó)高等教育滿意度調(diào)查報(bào)告[R].中國(guó)教育報(bào),2017-05-17(4).
[17]國(guó)家全文標(biāo)準(zhǔn)公開(kāi)系統(tǒng)[EB/OL].http://www.gb688.cn/bzgk/gb/.
[18]全國(guó)標(biāo)準(zhǔn)信息公共服務(wù)平臺(tái)[EB/OL].http://www.std.gov.cn/.
[19]全國(guó)團(tuán)體標(biāo)準(zhǔn)信息平臺(tái)[EB/OL].http://www.ttbz.org.cn/.
[20][22]國(guó)家教育標(biāo)準(zhǔn)體系研究課題組.國(guó)家教育標(biāo)準(zhǔn)體系的發(fā)展與完善[J].教育研究,2015(12):4-11.
[21]趙劍男,張勇.團(tuán)體標(biāo)準(zhǔn)與我國(guó)標(biāo)準(zhǔn)體系協(xié)同發(fā)展模式研究[Z].2017年第二屆“團(tuán)體標(biāo)準(zhǔn)研究與實(shí)踐”研討會(huì),2017-10-16.
[24]高等學(xué)校教學(xué)指導(dǎo)委員會(huì)[EB/OL].https://baike.baidu.com/item/高等學(xué)校教學(xué)指導(dǎo)委員會(huì)/1824904.
[25]潘懋元.高等教育大眾化的教育質(zhì)量觀[J].江蘇高教,2000(01).
[26]潘懋元.新時(shí)期中國(guó)高等教育的質(zhì)量戰(zhàn)略[J].中國(guó)大學(xué)教學(xué),2004(01).
Higher Education Quality Project: Review and Reflection
——on the Re-standardization of “National Standards”
YUAN Haijun?? (Changchun Guanghua University, Changchun, Jilin 130033, China)
Abstract: ?“Higher Education Quality Project” is the general term of a series of higher education teaching reform and quality construction plans organized and implemented by the state since the 1990s. According to the different goals and tasks, this plan can be divided into three periods: “educational reform project” “quality project” and “undergraduate teaching project”. The implementation of the “project” of higher education quality, to strengthen the teaching work center position and promote increased spending on teaching work in colleges and universities play an important role in such aspects, but there are “efficiency” and “fair”, “project management” and “routine management”, “the best education” and “suitable education” concept of deep conflict need to resolve in a timely manner. The newly released “national standards for undergraduate teaching quality in general institutions of higher learning” is one of the most important results of “higher education quality project”. To restart the re-standardization process in accordance with relevant national regulations is the primary task to enhance its status and function.
Key words: ???Higher Education Quality Project; undergraduate teaching; national standard; re-standardization

