數字搶椅子等

2008-07-02 09:17:38

中學科技 2008年6期

數字搶椅子

“搶椅子”的游戲相信大家一定不會陌生。由幾個小朋友圍成一圈，中間放上幾把椅子。主持者讓大家轉起來，當喊“停”時，轉圈的人要馬上就近搶一個椅子坐下來。因為人多椅子少，不可能每個人“保留一位”，必定會有人站在那里等著“受罰”。游戲規則簡單，方便易行，很受大家的喜歡。

下面有一道由空格組成的算式，算式正好是用1、2、3、4、5、6、7、8、9這九個數字中的八個填成。很顯然，這和大家玩的“搶椅子”的游戲很像，有九個數字，算式中只用八個，因此每一道算式中都會有一個數字不能夠參與其中。

看似數字們出場的機會均等。其實，通過實踐和觀察發現，有的數字是必然要填的，也就是說離開了它，這樣的算式根本就填不成功。

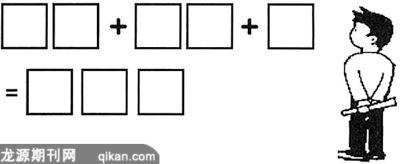
這里想讓你思考的就是這個問題：哪些數字是必定不能缺少的？

聰明的你可能會馬上回答，數字1是不能夠缺的。對，因為加數中有兩個兩位數和一個個位數，它們和的百位上的數字只能夠是1。

如果說1搶不到位置，這樣的等式誰也別想填成了。

你還沒有完整回答這個問題：那么，還有哪些數字是至關重要而缺一不可的呢？想想看。

奇偶分離

這可是一道奇妙的算式。請你在空格內填入數字1、2、3、4、5、6、7、8，使它們形成一道等式，結果為13572648。

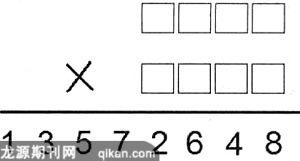
這可不是一般人能夠填寫出來的。你有興趣挑戰一下自己嗎？你也可以和你的同學一起來做這道題目，看看誰能先做出來。試一試吧。

唯一的答案

今年是奧運年，少不了要出些與2008有關的題目。有一個帶分數，它的整數部分是兩個數字，表示著2008年所在的世紀數，分數部分的分母是個兩位數，分子是個五位數，它們化簡后就得到2008。

便于理解，將其寫作算式□□＋□□□□□÷□□＝2008。

有趣的是，這個算式的空格內要填寫的數字恰好是1、2、3、4、5、6、7、8、9，你能夠填上來嗎？

由“它的整數部分是兩個數字，表示著2008年所在的世紀數”已知整數部分的兩個數字是2、1，其余的數字為3、4、5、6、7、8、9，若想讓它們組成□□□□□÷□□＝1987來，只有通過估算與嘗試。五位數的萬位數字只能為較大或最大，因為34的1987倍已經是67558了。（哈哈，真可惜，如果說到這里能夠看到答案，那有多么巧呀，只是67558中出現了兩個5而少了數字9。你發現了嗎？）

最為科學的方法是將1987分解質因數，然后通過調整找到此題的唯一的答案：

21＋95376÷48＝2008

練習：

在下面的算式中，也用上了加減乘除與數字1、2、3、4、5、6、7、8、9各一次，你能寫成這樣一道等式嗎？

□□□×□□÷□□＋□－□＝2008

巧了，它也只有一種答案。如果你能夠順利填出，你離天才真的不遠了。

本期答案

數字“搶椅子”

要想填成題目中要求的等式，數字1、4、8是必不可少的。如果說在算式中不使用這三個數字，你根本就填不成等式。不信你來試試看。

奇偶分離

讓這八個數字組成算式，能夠得出這八個數字已屬不易，再想讓它們乖乖地聽話，讓奇數數字與偶數數字各站一邊，好像是想都不用想的事了。其實不然，只要你能夠細心加耐心地來分析一下，不難找出它們的答案。

最為簡便的方法是分解1 3 5 7 2 6 4 8這個八位數的質因數，然后再來逐步調整，最后可以得到答案。