An Immune Self-adaptive Differential Evolution Algorithm with Application to Estimate Kinetic Parameters for Homogeneous Mercury Oxidation*

HU Chunping (胡春平) and YAN Xuefeng (顏學(xué)峰)

?

An Immune Self-adaptive Differential Evolution Algorithm with Application to Estimate Kinetic Parameters for Homogeneous Mercury Oxidation*

HU Chunping (胡春平) and YAN Xuefeng (顏學(xué)峰)**

Automation Institute, East China University of Science and Technology, Shanghai 200237, China

A new version of differential evolution (DE) algorithm, in which immune concepts and methods are applied to determine the parameter setting, named immune self-adaptive differential evolution (ISDE), is proposed to improve the performance of the DE algorithm. During the actual operation, ISDE seeks the optimal parameters arising from the evolutionary process, which enable ISDE to alter the algorithm for different optimization problems and improve the performance of ISDE by the control parameters’ self-adaptation. The performance of the proposed method is studied with the use of nine benchmark problems and compared with original DE algorithm and other well-known self-adaptive DE algorithms. The experiments conducted show that the ISDE clearly outperforms the other DE algorithms in all benchmark functions. Furthermore, ISDE is applied to develop the kinetic model for homogeneous mercury (Hg) oxidation in flue gas, and satisfactory results are obtained.

differential evolution, immune system, evolutionary computation, parameter estimation

1 Introduction

Differential evolution (DE) [1] is a new generation evolutionary algorithm (EA) and has been successfully applied to solve a wide range of optimization problems. Differential evolution is stochastic, population- based, and direct search algorithm for globally optimizing functions with real valued parameters. In the first international IEEE Competition on evolutionary optimization, DE proved to be one of the fastest EAs. Storn and Price [1] have compared DE with adaptive simulated annealing [2], the annealed Nelder and Mead approach [3], the breeder genetic algorithm [4], the EA with soft genetic operators [5], and the method of stochastic differential equations [6]. In most instances, DE outperformed all of the above minimizations approaches. Vesterstrom and Thomsen [7] applied 34 widely used benchmark problems to evaluate the performance of DE, particle swarm optimization (PSO) [8], and EA. Their study shows that DE generally outperforms the other algorithms. Krink. [9] introduced three search approaches [genetic algorithm (GA) [10], PSO, and DE] to develop bank rating systems, respectively, and turned out that DE is clearly and consistently superior compared with GA and PSO both in respect to precision and reliability.

In recent years, researchers have developed various strategies for adjusting control parameters dynamically. Abbass [15] proposed a self-adaptive Pareto DE (SPDE). In SPDE, the mutation rate is sampled for each individual from a Gaussian distribution,(0, 1). The crossover rate is first initialized for each individual from a uniform distribution,(0, 1). Then, CR is adapted as

where

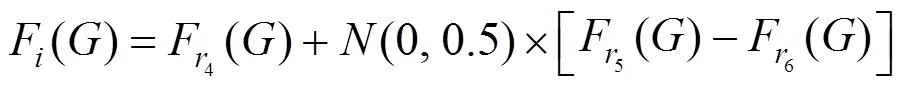
In self-adaptation parameter control, the idea of an evolutionary search can be used to implement the self-adaptation of search parameters [19]. In other words, the concept of coevolution can be used to adapt the control parameters. Coevolution method is an effective approach to decompose complex structure and achieve better performance. Several applications of coevolution method, which have been proven to be useful, were described in the literatures [20-22]. In this article, the immune concepts and methods are applied to determine the parameter setting of DE. Further, the proposed method, named immune self-adaptive differential evolution (ISDE), is compared with the versions of DE proposed by Price and Storn [23], the SPDE proposed by Abbass [15], and the self-adaptive DE (SDE) proposed by Omran[16].

For illustration, ISDE was applied to develop the kinetic model for homogeneous mercury (Hg) oxidation in flue gas. Homogeneous mercury oxidation in flue gas is a highly nonlinear reaction with reference to optimal operating conditions with many equality and inequality constraints. The kinetic model involves five reactions. Two of these reactions are reversible and three are irreversible. The preexponential factor and activation energy values in the rate constant term for each reaction need to be determined. Then, ISDE was used to determine the kinetic parameters for homogeneous mercury oxidation in flue gas with the data obtained in a laboratory scale apparatus, reported by Agarwal. [24, 25], and the kinetic model with good precision for homogeneous mercury oxidation in flue gas was developed.

2 Differential evolution algorithm

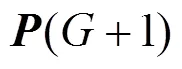
The procedure of executing DE can be described in the following:

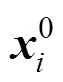
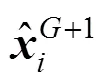
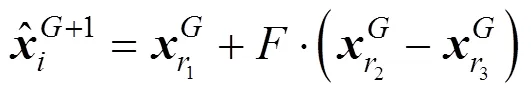
(7) Repeat steps 2-6 as long as the number of generations is smaller than the allowable maximum numbermand the best individual is not obtained.

The mutation strategy described above is known as DE/rand/1, meaning that the vector to be perturbed is randomly chosen, and that the perturbation consists of one weighted difference vector. DE/rand/1 is the most successful and the most widely used strategy [14].Other useful strategies are:

“DE/rand-to-best/1”:

“DE/best/2”:

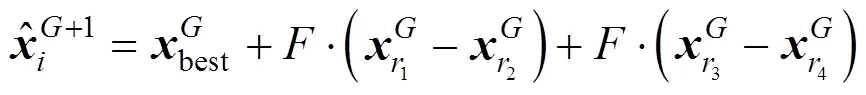
“DE/rand/2”:

3 Immune Self-adaptive Differential Evolution

In self-adaptation parameter control, the idea of an evolutionary search can be used to implement the self-adaptation of search parameters. The parameters to be adapted are coded into the chromosomes that undergo mutation and recombination. Better values for these encoded parameters are supposed to result in better individuals that in turn are more likely to survive and produce offspring and hence propagate better parameter values [19]. In other words, self-adaptation is a strategy in which the idea of an evolutionary search was used to choose the optimal parameters.

Immune system, a highly evolved biological system with learning, memory, and pattern recognition capabilities [26], has been successfully integrated into many other evolution algorithms [27-29]. In our work, the immune concepts and methods are applied to determine the parameter setting of DE. To be exact, the aim of leading immune concepts and methods into DE is theoretically to use the previous state information of search for seeking the optimal parameters,and CR. During the actual operation, ISDE seeks the optimal parameters arising from the evolutionary process, which enable ISDE to alter the algorithm for different optimization problems and improve the performance of ISDE by the control parameters’ self-adaptation. In ISDE, the first initial antibodies are randomly generated within the feasible range. The two parameters of each individual are initialized from a normal distribution within the feasible range. The affinity values of the antibodies are calculated. Then, depending on the affinity values, the parameters are replaced by antibody with a certain probability defined previously. In each generation, a percentage of antibodies in the antibody population are replaced by created new antibodies. Thus, the coevolution method is established. Differential evolution is used to perform evolution search in spaces of solutions, and immune system is used to perform evolution search in spaces of control parameters. The solutions and control parameters evolve interactively and selfadaptively, and both the satisfactory solutions and suitable control parameters can be obtained simultaneously.

The procedure of executing ISDE can be described in the following:

(1) Initialization operation

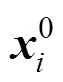
(3) Mutation operation

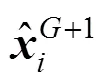
(4) Crossover operation

(5) Evaluation operation

(6) Create new antibodies

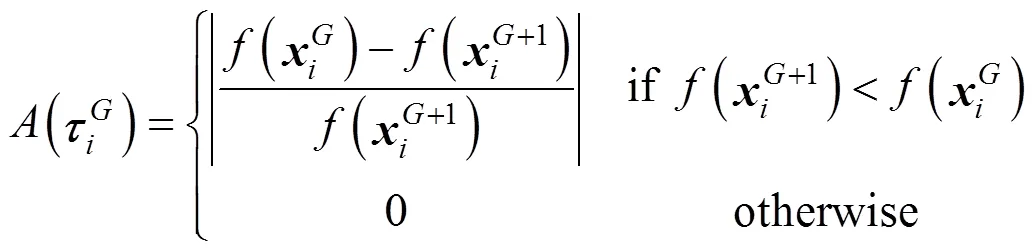
(7) Update antibodies

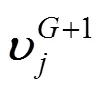
(8) Generate the parameters for next generation

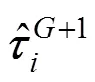
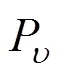
whereis the parameter that controls the probability between different antibodies.

(10) Repeat steps 2-9 as long as the number of generations is smaller than the allowable maximum numbermand the best individual is not obtained.

4 Benchmark function

Nine benchmark functions were used in our experimental studies. These benchmark functions were divided into three classes: functions with single optima, many local minima, and a few local minima. The benchmark functions are given in Table 1.stands for the dimension of the function,0denotes their ranges, andminis a function value of the global optimum. A more detailed description of each function is given in Yao. [30], Krink. [31], and Salman[32].

5 Experimental results

Maximal number of evaluations: 50000;

The results reported in this section are average results of 30 independent runs.

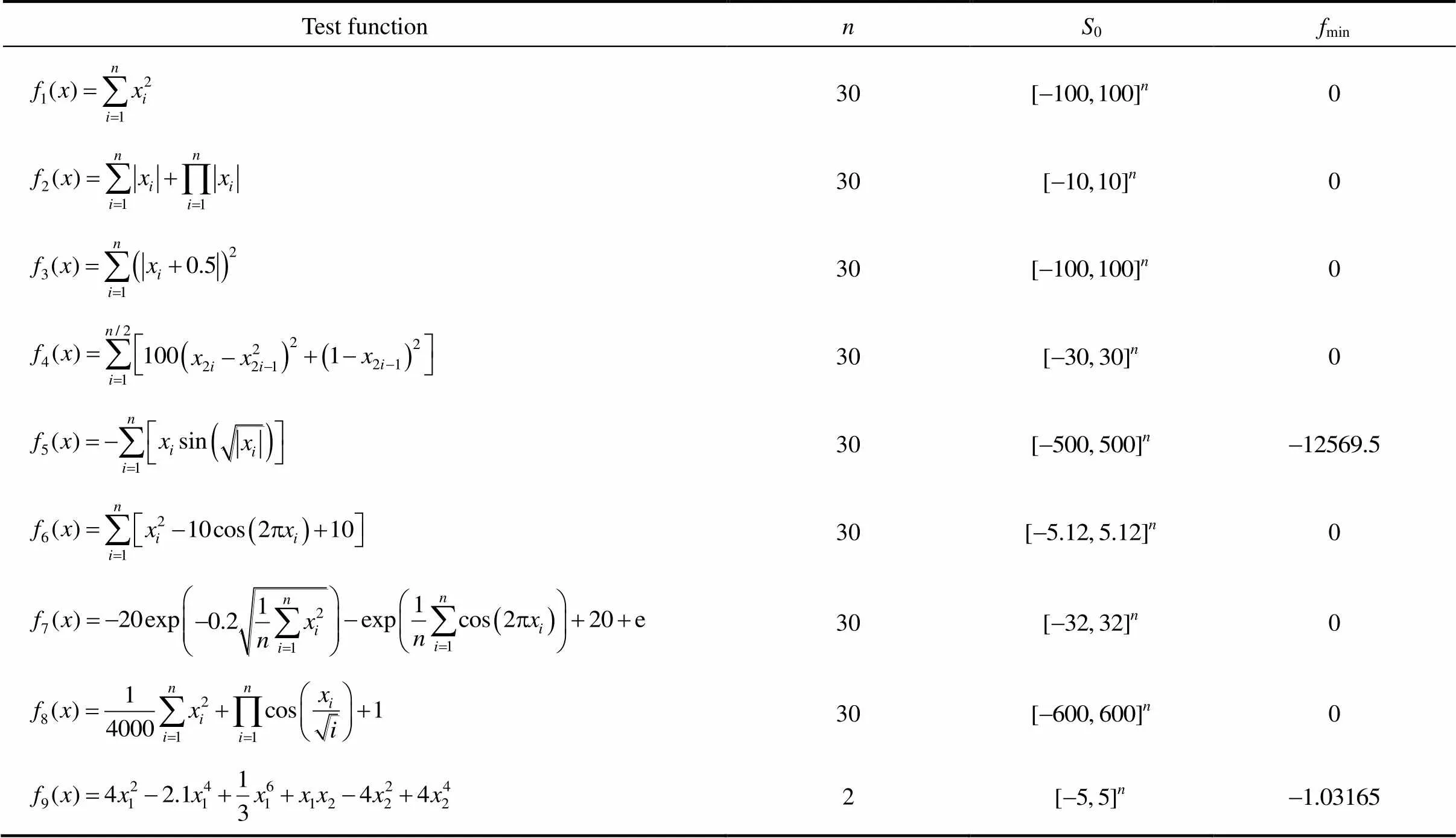
Table 1 Benchmark function

5.1 No-noisy benchmark functions

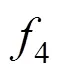
Table 3 summarizes the results obtained by applying the different approaches to the multimodal benchmark functions. The results show that the ISDE significantly outperformed (or at least equal to) the other methods in all the multimodal functions.

From above experiments, it can be turned out that ISDE is clearly superior compared with the original DE strategies, SPDE, and SDE in all benchmark functions.

5.2 Noisy benchmark functions

In this subsection, the effect of noise on the performance of ISDE is investigated. The noisy versions of the benchmark functions are defined as:

Table 4 and Table 5 summarize the results obtained for the noisy problems for the unimodal and multimodal functions, respectively. Table 4 and 5 show that the ISDE was less prone to noise than other DE strategies for all benchmark functions. The ISDE retained its position as the best performer when applied to all benchmark functions even in the presence of noise. The only exception is the noisy Rastrigin’s function where SDE outperformed the ISDE. However, even for the noisy Rastrigin’s function where ISDE’s average is worse than SDE, it is not significantly worse. In addition, the improvement is even more significant for the noisy Ackley’s function, where all strategies were trapped in a local optimum. Hence, compared with the other tested strategies, the ISDE seems to be less badly affected by noise. This is a significant improvement over the conventional DE, which is not a good approach to achieve results with high accuracy for noisy functions [31].

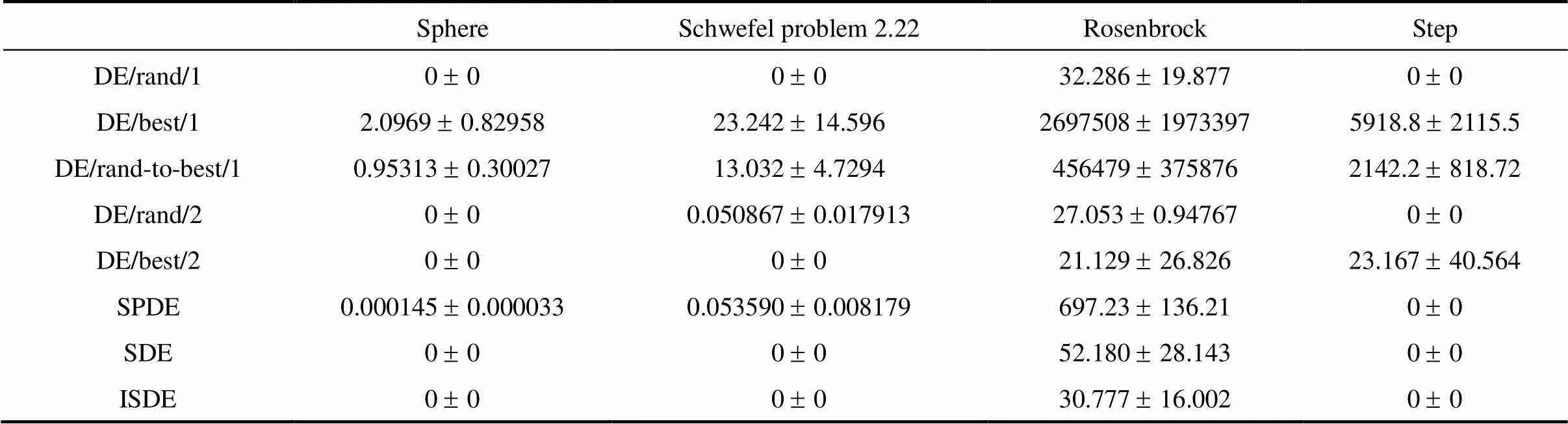
Table 2 Mean and standard deviation (±SD) of the unimodal function optimization results (The data about DE/rand/1, DE/best/1, DE/rand-to-best/1, DE/rand/2, DE/best/2, SPDE, and SDE were reported by Salman et al. [32])

Table 3 Mean and standard deviation (±SD) of the multimodal function optimization results (The data about DE/rand/1, DE/best/1, DE/rand-to-best/1, DE/rand/2, DE/best/2, SPDE, and SDE were reported by Salman et al. [32])

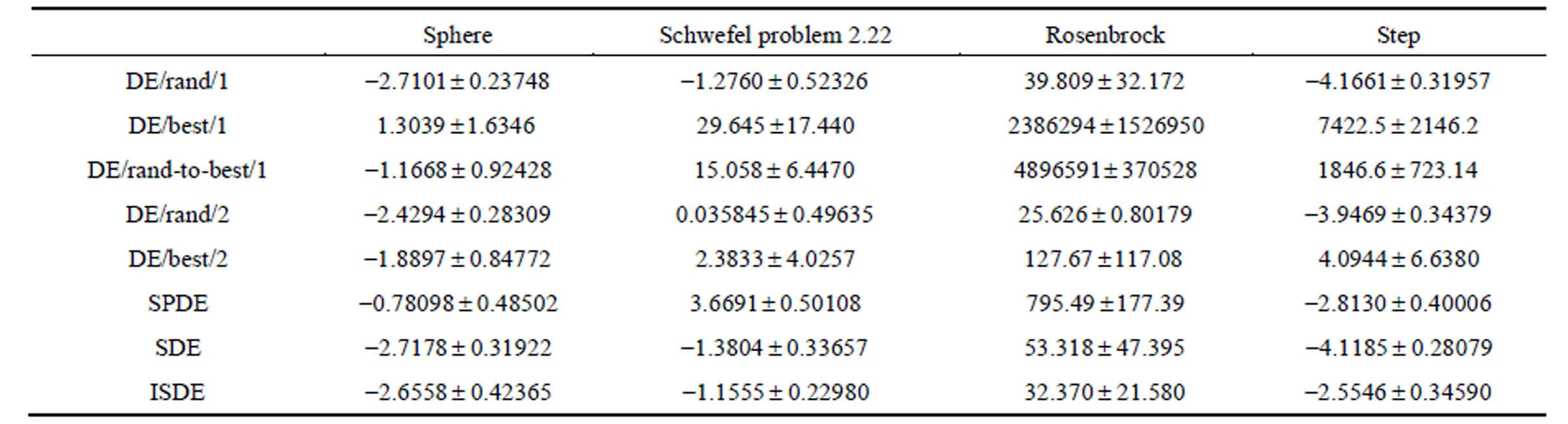
Table 4 Mean and standard deviation (±SD) of the noisy unimodal function optimization results (The data about DE/rand/1, DE/best/1, DE/rand-to-best/1, DE/rand/2, DE/best/2, SPDE, and SDE were reported by Salman et al. [32])

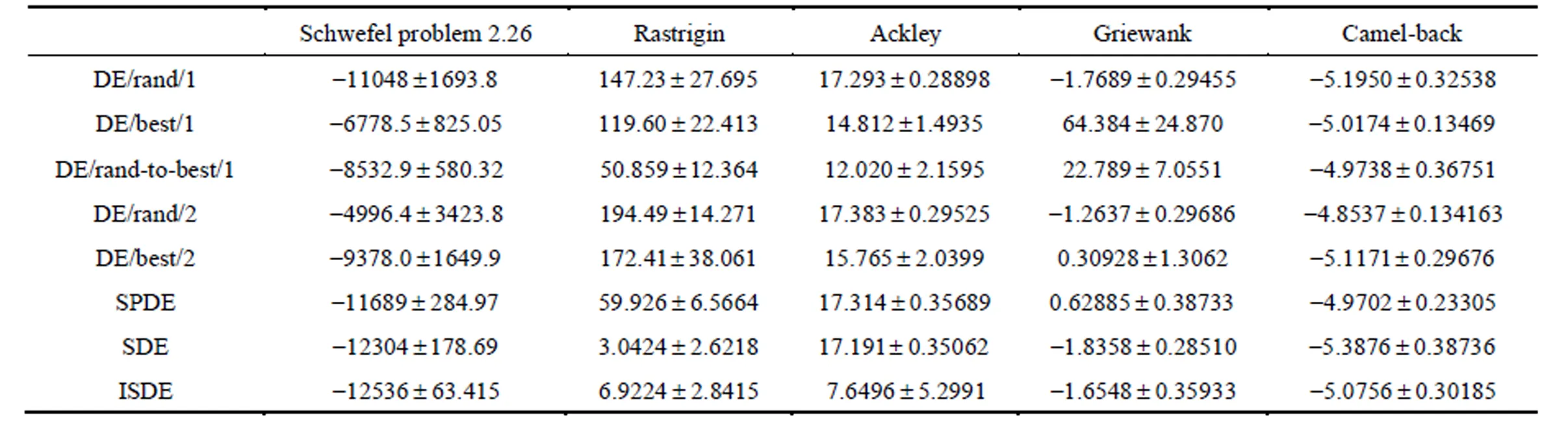
Table 5 Mean and standard deviation (±SD) of the noisy multimodal function optimization results (The data about DE/rand/1, DE/best/1, DE/rand-to-best/1, DE/rand/2, DE/best/2, SPDE, and SDE were reported by Salman et al. [32])

5.3 Effect of α, β, and

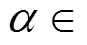
6 Application

Mercury emissions from coal-fired power plants are highly dependent upon mercury speciation [33]. Mercury in the flue gas is most commonly classified in three forms: elemental mercury (Hg0), oxidized mercury (Hg2+), and particulate bound mercury (HgP). The particulate bound mercury is usually trapped by ash collection devices within power plants, such as electrostatic precipitators, mechanical hoppers, or bag houses. Elemental mercury is relatively inert and difficult to capture because of its nonreactivity. It is also volatile at high temperatures and insoluble in water. In contrast, oxidized mercury is very water soluble and has an affinity for adsorbing onto particulate matter such as fly ash or on metal surfaces in the duct. As a result of these physical and chemical properties of Hg0and Hg2+, the removal of mercury is enhanced when elemental Hg is converted to its oxidized form [34].

In order to better understand the reaction mechanism that takes place in the gas phase, a model needs to be developed where the percentage of mercury oxidized can be predicted based on the concentrations of these flue gas components. The reaction mechanism, proposed by Agarwal and Stenger [34], is a five-reactionsystem, where two reactions are reversible and three reactions are irreversible. These reactions are listed below:

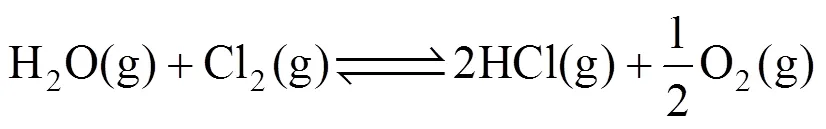
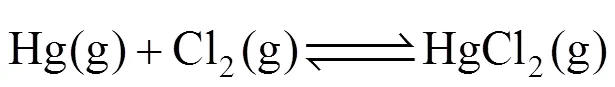
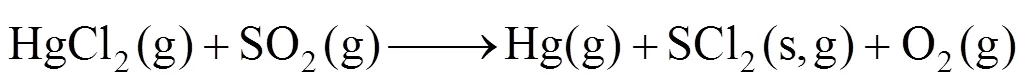
where the term (s, g) denotes that the species could be in solid (s), gas (g) or both phases.

The reaction rate equations can be written as follows:

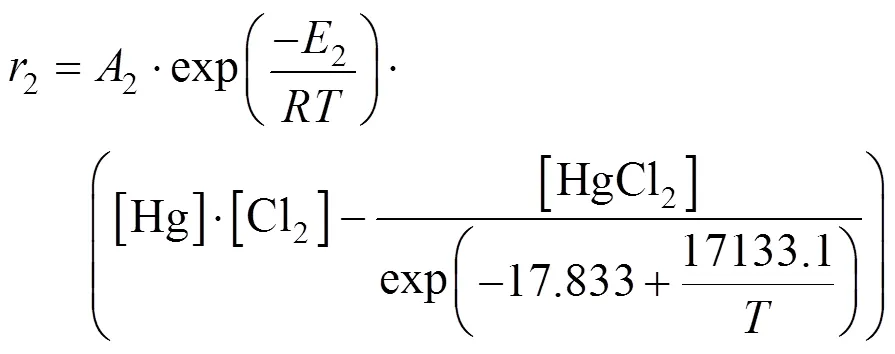
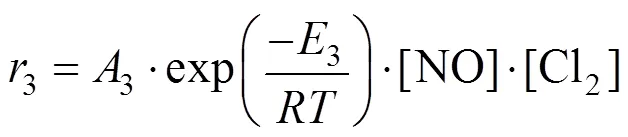
Table 6 Influence of α on the performance of ISDE

Table 7 Influence of β on the performance of ISDE

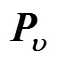
Table 8 Influence of??on the performance of ISDE

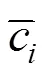
Table 9 Optimal parameters and objective function values corresponding to reported data [34] and ISDE

7 Conclusions

This article presents an efficient self-adaptive DE algorithm for global optimization. In the proposed method, the immune concepts and methods are applied to determine the parameter setting, which utilizes the previous state information of search for seeking the optimal parameters,and CR. In the benchmark tests, both noisy and nonoisy functions, the results show that the performance of ISDE is outstanding in comparison with the original DE strategies, SPDE and SDE tested. Among the tested strategies, the ISDE can rightfully be regarded as an excellent first choice when faced with a new optimization problem to solve. Thus, the algorithm was subsequently used to estimate the kinetic parameters for homogeneous mercury oxidation in flue gas. The results marked a noticeable improvement over previously reported solutions.

1 Storn, R., Price, K., “Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces”, Technical Report TR-95-012, International Computer Science Institute, Berkeley, CA, USA (1995).

2 Ingber, L., “Simulated annealing: Practicetheory”,..., 18, 29-57 (1993).

3 Press, W.H., Teukolsky, S.A., Vetterling, W.T., Flannery, B.P., Numerical Recipes in C, Cambridge University Press, UK (1992).

4 Muehlenbein, H., Schlierkamp, V., “Predictive models for the breeder genetic algorithm (I) Continuous parameter optimizations”,.., 1, 25-49 (1993).

5 Voigt, H.M., “Soft genetic operators in evolutionary algorithms”,, 899, 123-141 (1995).

6 Aluffi-Pentini, F., Parisi, V., Zirilli, F., “Global optimization and stochastic differential equations”,..., 47, 1–16 (1985).

7 Vesterstrom, J., Thomsen, R., “A comparative study of differential evolution, particle swarm optimization, and evolutionary algorithms on numerical benchmark problems”, In: Proceedings of the Sixth Congress on Evolutionary Computation, IEEE Press, USA, 332-339 (2004).

8 Eberhart, R., Kennedy, J., “A new optimizer using particle swarm theory”, In: Proceedings of the Sixth International Symposium on Micromachine and Human Science, IEEE Press, Nagoya, Japan, 39-43 (1995).

9 Krink, T., Paterlini, S., Resti, A., “Using differential evolution to improve the accuracy of bank rating systems”,..., 52, 68-87 (2007).

10 Holland, J.H., Adaptation in Natural and Artificial Systems, University of Michigan Press, Ann Harbor (1975).

11 Brest, J., Bo?kovi?, B., Greiner, S., ?umer, V., Mau?ec., M., “Performance comparison of self-adaptive and adaptive differential evolution algorithms”,., 11, 617-629 (2007).

12 Liu, J., Lampinen., J., “A fuzzy adaptive differential revolution algorithm”, In: Proceedings of the IEEE International Region 10 Conference on Computers, Communications, Control and Power Engineering, IEEE Press, Beijing, China, 606-611(2002).

13 Storn, R., “On the usage of differential evolution for function optimization”, In: Biennial Conference of North American Fuzzy Information Processing Society, IEEE Press, Berkeley, USA, 519–523 (1996).

14 Babu, B., Jehan, M., “Differential evolution for multi-objective optimization”, In: Proceedings of the IEEE Congress on Evolutionary Computation, IEEE Press, Canberra, Australia, 2696-2703 (2003).

15 Abbass., H., “The self-adaptive pareto differential evolution algorithm”, In: Proceedings of the IEEE Congress on Evolutionary Computation, IEEE Press, Hawaii, USA, 831-836 (2002).

16 Omran, M., Salman, A., Engelbrecht, A., “Self-adaptive differential evolution”, In: Proceedings of the International Conference on Computational Intelligence and Security, IEEE Press, Xi’an, China, 192-199 (2005).

17 Yuan, X.H., Zhang, Y., Wang, L., Yuan, Y.B., “An enhanced differential evolution algorithm for daily optimal hydro generation scheduling”,..., 55, 2458-2468 (2008).

18 Nobakhti, A., Wang, H., “A simple self-adaptive differential evolution algorithm with application on the ALSTOM gasifier”,.., 8, 350–370 (2008).

19 Eiben, A., Hinterding, R., Michalewicz, Z., “Parameter control in evolutionary algorithms”,..., 3, 124-141 (1999).

20 Carlos, A.C.C., “Use of a self-adaptive penalty approach for engineering optimization problems”,.., 41, 113-127 (2000).

21 He, Q., Wang, L., “An effective co-evolutionary particle swarm optimization for constrained engineering design problems”,...., 20, 89-99 (2007).

22 Hu, F.Z., Wang, L., He, Q., “An effective co-evolutionary differential evolution for constrained optimization”,..., 186, 340-356 (2007).

23 Storn, R., Price, K., “Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces”,.., 11, 341-359 (1997).

24 Agarwal, H., Stenger, H.G., Wu, S., Fan, Z., “Effects of H2O, SO2and NO on homogeneous Hg oxidation by Cl2”,.., 20, 1068-1075 (2006).

25 Agarwal, H., Romero, C.E., Stenger, H.G., “Comparing and interpreting laboratory results of Hg oxidation by a chlorine species”,.., 88, 723-730 (2007).

26 Farmer, J.D., Packard, N.H., Perelson, A.S., “The immune system, adaptation, and machine learning”,., 2, 187-204 (1986).

27 Wu, X.L., Lu, J.G., Sun, Y.X., “An improved differential evolution for optimization of chemical process”,...., 16, 228-234 (2008).

28 Jiao, L.C., Wang, L., “A novel genetic algorithm based on immunity”,..., 30, 552-561 (2000).

29 Zeng, C.W., Gu, T.L., “A novel immunity-growth genetic algorithm for traveling salesman problem”, In: Proceedings of IEEE Conference on Natural Computation, IEEE Press, Haikou, China, 394-398 (2007).

30 Xin, Y., Liu, Y., Lin, G.M., “Evolutionary programming made faster”,..., 3, 82-102 (1999).

31 Krink, T., Filipi?, B., Fogel, B., “Noisy optimization problems—A particular challenge for differential evolution?”, In: Proceedings of the IEEE Congress on Evolutionary Computation, IEEE Press, Portland, USA, 332-339 (2004).

32 Salman, A., Engelbrecht, A., Omran, M., “Empirical analysis of self-adaptive differential evolution”,...., 83, 785–804 (2007).

33 Niksa, S., Helble, J.J., Fujiwara, N., “Kinetic modeling of homogeneous mercury oxidation: The importance of NO and H2O in predicting oxidation in coal-derived systems”,..., 35, 3701-3706 (2001).

34 Agarwal, H., Stenger, H.G., “Development of a predictive kinetic model for homogeneous Hg oxidation data”,..., 45, 109-125 (2007).

2008-07-28,

2008-12-24.

the National Natural Science Foundation of China (20506003, 20776042) and the National High-Tech Research and Development Program of China (2007AA04Z164).

** To whom correspondence should be addressed. E-mail: yan_xuefeng@hotmail.com