Kinetic Rate Constant of Liquid Drainage from Colloidal Gas Aphrons*
Luo Jianhong (羅建洪), LI Jun (李軍)**, HUANG Ping (黃平) and HUANG Meiying (黃美英)
?
Kinetic Rate Constant of Liquid Drainage from Colloidal Gas Aphrons*
Luo Jianhong (羅建洪), LI Jun (李軍)1,**, HUANG Ping (黃平)1and HUANG Meiying (黃美英)2
1Department of Chemical Engineering, Sichuan University, Chengdu 610065, China2Chongqing Three Gorges University, Chongqing 404000, China
A kinetic model fitted by the empirical equation has been proposed to describe the liquid drainage behavior. Rate constants (d) of liquid drainage equation could be obtained from the above empirical equation. In this paper, the stability of the colloidal gas aphrons (CGAs), the effect of concentrations of sodium dodecyl benzene sulphate (SDBS), dodecyl trimethylammonium bromide (HTAB) and polyoxyethylene sorbitol anhydride monolaurate(Tween-20), temperature, stirring speed, stirring time, and various kinds of salts on thedof liquid drainage are further investigated. The results show that the Arrhenius equation can be successfully used to describe the relation betweendand absolute temperature (), and concentrations of surfactants, stirring speed, stirring time and salinities also have great effect on thed. At last, the CGAs drainage mechanism is explained from analysis of the rate of liquid drainage as a function of time.
colloidal gas aphrons, liquid drainage, stability, rate constants
1 Introduction
Colloidal gas aphrons(CGAs) are firstly proposed by Sebba [1], which consist of a microbubble encapsulated in a thin aqueous film(“soapy shell”). The most striking features of CGAs [1-3] are as follows: (1) CGAs expose a large interfacial area per unit volume for the adsorption of molecules as a result of their small size and high gas hold-up,.., the volumetric gas ratio in the gas-liquid dispersion is typically around 50%; (2) The flow properties of CGAs dispersions are similar to those of water (.. CGAs can be easily pumped without collapse); (3) The aphron phase can be separated easily from the bulk liquid phase because of its buoyancy. Typically, the liquid-dispersion interface will start to rise in less than a minute.
As a consequence of these properties, researchers have considered various applications for CGAs with focus on flotation separation technique [4]. For example, a number of applications have been reported for CGAs including removal of fine sulphur particles from NTA [5], selective recovery of valuable components of whey [6], protein recovery [3], removal of heavy metals from aqueous solutions [7], and separation of organic dyes from waste water [8, 9]. It is important to introduce another effective, novel separation technique—predispersed solvent extraction (PDSE), which involve in an essential flotation using CGAs [1]. In many separation processes, the effectiveness of a CGA is related to its stability. Therefore, investigation on the stability of CGAs presents much importance for characterization of CGA dispersions and for applications in separation technology. Generally, the stability of aqueous foam is determined by two different phenomena [10]: the rate at which liquid drains from foam, and the rate at which the body of the foam breaks down. In the case of CGAs, there is no perceptible breakdown of the microbubble until the great majority of the liquid has drained from CGAs [11]. In this condition, the drainage from CGAs is almost completely unaffected by the microbubble breakdown. Therefore, the rate ordof liquid drainage from CGAs becomes paramount measure of stability.
Few of the studies on liquid drainage of CGAs were reported in the literature [2, 6, 11]. Amiri [6] have made a predictive model for liquid drainage for liquid drainage rate of CGAs. Save [2] have proposed a model for liquid drainage with the aim to interpret the mechanism of drainage. Yan. [11] have propounded a kinetic model, which successfully describes the liquid drainage profiles of CGAs. Therefore, in this paper, based on the mathematics model proposed by Yan. [11], the rate constant of liquid drainage is further studied to investigate the effects of various parameters ond.
2 ExperimentAL
2.1 Materials
The surfactants used in this work are sodium dodecyl benzene sulphate [SDBS (AR grade)], dodecyl trimethylammonium bromide [HTAB (AR grade)] and polyoxyethylene sorbitol anhydride monolaurate [Tween-20 (AR grade)] and pure water is produced by Aquapro making-water machine (ABZ1-1001-P).
2.2 Extraction preparation and procedure
SDBS (anionic) at the concentration of 0.21, 0.42, 0.63, 0.84, 1.05 g·L-1, HTAB(cationic) at the concentration of 0.225, 0.45, 0.675, 0.9, 1.125 g·L-1, and Tween-20 (nonionic) at the concentration of 3.4, 6.8, 10.2, 13.6, 17 g·L-1are chosen to study the effects of surfactants concentration ond. Inspecting the impact of temperature ond, the mass of SDBS is 0.84 g·L-1, HTAB is 1.125 g·L-1and Tween-20 is 17 g·L-1. HTAB at the concentration of 1.125 g·L-1is taken to investigate the influence of the other parameters ond. CGA suspensions as shown in Fig. 1 are generated using a high-speed stirrer as the method by Sebba [12] as presented in Fig. 2. The surfactant solution of 200 ml is stirred at high speed (6000 r·min-1) for 3 min and a constant volume of white creamy CGAs are prepared. These CGAs can be kept dispersed under low stirring conditions (around 1000 r·min-1).

Figure 1 Samples of CGAs generated from HTAB in water are examined by a microscopic camera
Figure 2 Schematic of the CGA forming process
1—electric motor; 2—CGA; 3—baffles; 4—spinning disk
2.3 CGAs drainage
The liquid drainage rates are measured by observing the volume of the liquid drained as a function of time as shown in Fig. 3. Tests are conducted by pumping about 300 ml of CGAs suspension into the glass column with 2.5 cm inner diameter and 1.0 m height. The water jacket is to maintain the tube at a stable temperature.
3 Results and discussion
3.1 Effects of various parameters on kd
The empirical equation [11] has been proposed to describe the liquid drainage behavior. The equation is as follows:

Figure 3 Schematic diagram of the experimental setup for drainage of CGAs

whereVrefers to the volume of drained liquid at time,maxrefers to the maximum volume of drained liquid,describes the sigmoidal character of the curve andis equal to the half-life (1/2) of drainage.
Rate of liquid drainage can be obtained from the Eq. (1):

The relationship betweenandVcan be expressed as Eq. (3) from Eq.(1):
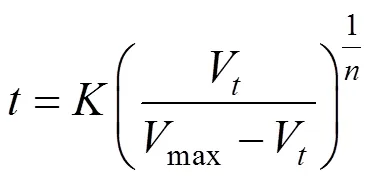
Substituting this equation into Eq. (2), the following kinetic equation can be derived:

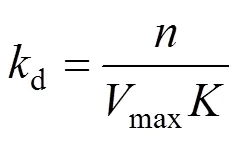
Thedrepresents the stability of CGAs.
3.1.1d
In the case of HTAB, SDBS and Tween 20, when the surfactant concentration is much below the CMC, stable CGA dispersions cannot be formed. Therefore, the all selected surfactant concentrations in this study are equal or above the corresponding CMC. The effect of surfactant concentration ondis shown in Fig. 4. It can be seen that the curves ofdconcentration of HTAB, SDBS and Tween-20 show a similar trend. With increasing surfactant concentration,ddecreases gradually and the better stability is obtained. This is because of an inverse relationship between the surfactant concentration and the radius of the aphrons with increasing surfactant concentration [13-15]. And Dai. [16] pointed out that the rate of liquid drainage is proportional to the bubble radius. The other reason may be ascribed to the increase of elasticity at higher concentration of surfactant [17]. Consequently, it will delay the coalescence of aphrons. Therefore, as the surfactant concentration increases,dalso decreases. Moreover, larger amount of aphrons should be formed at higher surfactant concentration.

Figure 4 The rate constantdthe surfactants concentration
▲?HTAB;◆?SDBS;●?Tween-20
3.1.2d
Figure 5 shows thatddecreases linearly with an increase in the stirring speed. The reason is that increasing stirring speed could increase the surface area due to the production of smaller bubbles [14].

Figure 5 The rate constantdthe stirring speed
Figure 6 The rate constantdthe stirring time

Figure 7 The rate constantdthe temperature
■?SDBS;●?HTAB;▲?Tween-20
3.1.3d
For a short stirring time, CGA is unstable and cannot be used for impurities recovery [14]. When stirring time increases to 1 min, the stability of CGA enhances dramatically. However, once the stirring time hit the certain value, the stability of CGA may decrease due to the collision of CGA. The effect of stirring time ondcan be seen in Fig. 6.
3.1.4d
The effect of temperature ondcan be described by the Arrhenius equation [11]:

wherea(J·mol-1) is activation energy and the coefficientdenotes the frequency factor,(J·K-1·mol-1) is the gas constant and(K) represents the absolute temperature.

Table 1 The hydrophile-lipophile balance (HLB) value ofsurfactants versus activation energy (Ea)
Increasing temperature will lead to reduce the viscosity of liquid and make thin liquid film, resulting in an increase in the rate of liquid drainage. The natural logarithm of the rate constant of liquid drainage from CGAs (lnd) determined at different temperatures is plotted against the reciprocal of the absolute temperature in Kelvin (1/) as shown in Fig. 7. A linear relationship is found between lndand 1/, which further justifies the application of Eq. (1) to the liquid drainage behavior of CGA dispersions. From the above results,aof different surfactants can be calculated respectively. The results are shown in Table 1. According to Arrhenius equation, the activation energyais interpreted as the activation energy for drainage. The activation energy of drainage for HTAB is larger than the other two surfactants, indicating that the liquid drainage from CGAs generated with HTAB need to overcome more activation energy than that of the other two surfactants.

Figure 8 The rate constantddifferent type of salts
■?NH4H2PO4;●?(NH4)2HPO4;▲?(NH4)3PO4
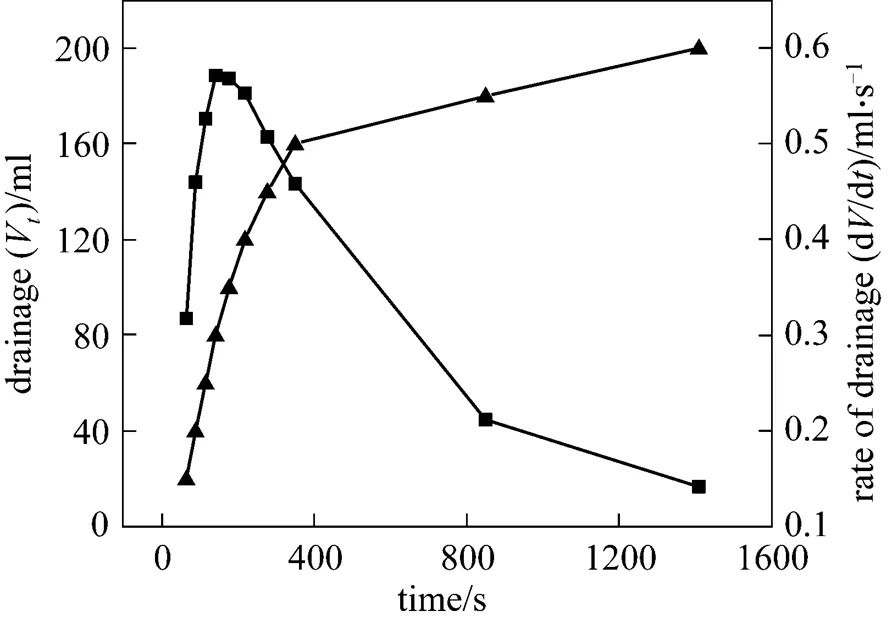
Figure 9 Rate of liquid drainage and drainageVtime
▲?drainageV;■?rate of drainage
3.1.5d
Salts addition had adverse effect on stability of CGA. The results are shown in Fig. 8. Thedvalue increases from 3.12×10-5to 8.36×10-5, 9.85×10-4and 2.92×10-4with addition of 2.5 g·L-1NH4H2PO4, (NH4)2HPO4and (NH4)3PO4on CGA generated from cationic surfactant HTAB at the concentration of 1.13 g·L-1, respectively. However, an interesting phenomenon is that at the experiment range, with increasing concentration of salinities,dwill decrease gradually. What is more surprising is that the effects of NH4H2PO4, (NH4)2HPO4and (NH4)3PO4ondshow the same trend. This is because the cationic surfactant HTAB includes ammonium ion with the addition of NH4H2PO4, (NH4)2HPO4and (NH4)3PO4, which will improve repulsive electrostatic interaction to stabilize the CGA. The result is different from the addition of NaCl by Chaphalkar [15] and Jarudilokkul [14].
3.2 Mechanism of liquid drainage
The correlation between rate of liquid drainage from CGAs and time can be derived from Eq. (2). The liquid drainage data of CGAs (surfactant, HTAB; concentration, 1.125 g·L-1; temperature, 303 K) selected as an example have been graphically differentiated to obtain the drainage rates, as shown in Fig. 9.
As can be seen from the Fig. 9, the drainage rate shows a rapid increase from the initial value to the maximum value of 0.5714 ml·s-1, and then it declines toward zero with increasing time. Thus, the whole drainage process can be divided into two stages. The first stage [2, 11] is dominated by gravity driven liquid drainage because the density of liquid phase is much higher than that of gas phase, which accounts for more than 90% of the total liquid. In the second stage, if the liquid membrane can be regarded as the capillary, the rate of liquid drainage is proportional to the film thickness of quartic equation according to Poiseuille’s equation. Thus, the rate of liquid drainage decreases drastically to zero with the thinning of films.
4 ConclusionS
Based on the results of this research on the rate constant of liquid drainage from colloidal gas aphrons, the following conclusions can be drawn:
(1) Arrhenius equation can be successfully used to describe the relation betweendand absolute temperature.
(2) The concentrations of surface active agents, stirring speed, stirring time, and especially, salinities have significant impact on thed.
(3) The HLB value of surface active agent has great influence on the activation energy (a). With increasing HLB value of surface active agent, the activation energy (a) goes up gradually.
(4) By analysis of the rate of liquid drainage as a function of time, the whole CGAs drainage process can be divided into two stages dominated by the gravity and the capillary, respectively.
1 Sebba, F., Foams and Biliquid Foams:Aphrons, Wiley, New York (1987).
2 Save, S.V., Pangarkar, V.G., “Characterization of colloidal gas aphrons”,..., 127, 35-53 (1994).
3 Jauregi, P., Gilmour, S., Varley, J., “Characterization of colloidal gas aphrons for subsequent use for protein recovery”,..., 65, 1-11 (1997).
4 Jauregi, P., Varley, J., “Colloidal gas aphrons: potential applications in biotechnology”,, 17, 390-395 (1999).
5 Amiri, M.C., “Sulphur removal from NTA dispersion by aphron flotation”, Ph.D. Thesis, Manchester University of Science and Technology, Manchester (1989).
6 Amiri, M.C., “Separation of ultra-fine sulphur particles from NTA dispersion by aphron flotation”,..., 3, 148-153 (1990).
7 Matsushita, K., Mollah, A.H., Stuckey, D.C., del Cerro, C., Bailey, A.I., “Predispersed solvent extraction of dilute products using CGA and CLA: Aphron preparation, stability and size”,., 69, 65-72 (1992).
8 Save, S.V., Pangarkar, V.G., Kumar, S.V., “Intensification of mass transfer in aqueous two-phase systems”,.., 41, 72-78 (1993).
9 Huang, Y.Y., Wang, Y.D., Dai, Y.Y., “Separation of organic dyes from water by colloidal gas aphrons”,, 7 (1), 46-51 (2002).
10 Jacobi, W.M., Woodcock, K. E., Grove, C.S., “Theoretical investigation of foam drainage”,..., 48, 2046 (1956).
11 Yan, Y.L., Qu, C.T., Zhang, N.S., Yang, Z.G., Li, L., “A study on the kinetics of liquid drainage from colloidal gas aphrons (CGAs)”,..:.., 259, 167-172 (2005).
12 Sebba, F., “An improved generator for micron-sized bubbles”,, (9), 91 (1985).
13 Zhang, C., Valsaraj, K.T., Constant, W.D., Roy, D., “Studies in solvent extraction using polyaphrons (I) size distribution, stability, and flotation of polyaphrons”,..., 31, 1059 (1996).
14 Jarudilokkul, S., Rungphetcharat, K., Boonamnuayvitaya, V., “Protein separation by colloidal gas aphrons using nonionic surfactant”,..., 35, 23-29 (2004).
15 Chaphalkar, P.G., Valsaraj, K.T., Roy, D., “A study of the size distribution and stability of colloidal gas aphrons using a particle size analyzer”,..., 28 (6), 1287-1302 (1993).
16 Dai,Y.J., Deng, T., “Stabilization and characterization of colloidal gas aphron dispersions”,..., 261, 360-365 (2003).
17 Rosen, M.J., Surfactants and Interfacial Phenomena, Wiley, 123-141, 200-220 (1978).
2008-11-27,
2009-07-07.
the Eleventh Five Year National Key Technology R&D Program (2008BAE58B01) and New Century Excellent Talents of Ministry of Education (NCET-07-0577), the People’s Republic of China.
** To whom correspondence should be addressed. E-mail: lijun@email.scu.edu.cn
 Chinese Journal of Chemical Engineering2009年6期
Chinese Journal of Chemical Engineering2009年6期
- Chinese Journal of Chemical Engineering的其它文章
- Effect of Working Temperature on the Resistance Characteristic of aPleated Stainless Steel Woven Filter*
- The Numerical Simulation of Collapse Pressure and Boundary of the Cavity Cloud in Venturi*
- Performance of Inner-core Supersonic Gas Separation Device with Droplet Enlargement Method*
- Void Fraction Distributions in Cold-gassed and Hot-sparged Three Phase Stirred Tanks with Multi-impeller*
- Kinetics of COD Removal in a Biological Aerated Filter in thePresence of 2,4,6-Trinitrophenol (Picric Acid)*
- Representation of Phase Behavior of Ionic Liquids Using the Equation of State for Square-well Chain Fluids with Variable Range*
