弧面分度凸輪CAD 技術研究

牟小云

（陜西理工學院機械工程學院，陜西 漢中 723003）

弧面分度凸輪機構（Roller Gear Cam Mechanism）：又稱滾子齒式凸輪分度機構，它主要是由裝在箱體內的一個空間凸輪和在徑向放射狀等分地裝有滾子的從動盤組成。該機構由輸入軸上的弧面凸輪與輸出軸分度盤上的滾子無間隙垂直嚙合，由凸輪廓面實現分度盤轉位和分度盤靜止、定位自鎖，從而將輸入的連續回轉運動轉化為輸出的間歇回轉運動。它具有結構簡單、剛性好、重量輕、承載能力強、運轉平穩、定位準確等特點，可用于高速場合，是目前工作性能最好的間歇轉位機構，廣泛應用于包裝、食品、印刷、煙草、沖壓等自動、半自動加工機械，還用于各種機械手、自動生產線。但眾所周知，弧面分度凸輪工作輪廓面是空間不可展曲面，很難用常規的機械制圖方法繪制，且計算非常復雜，所以在具體繪制時多采用計算機輔助繪圖。本文采用編程語言 VC++、逆向工程軟件Imerageware、CAD/CAM 集成軟件UG 及來共同完成弧面分度凸輪的三維實體模型的繪制。

1 弧面分度凸輪廓面點坐標的計算

1.1 設計計算原理

弧面分度凸輪的設計計算目前一般按照空間包絡曲面的共軛原理進行設計計算[1-3]，建立其數學模型。由凸輪和轉盤的相對位置和嚙合關系建立如圖1所示的四套右手坐標系。其中圖1(a)為面對2X 箭頭看，滾子在距2O 為r 處垂直于X2軸的截面；圖1(b)為面對 Z1箭頭看，通過凸輪中心1O并垂直于1Z半徑為1pr的凸輪截面。

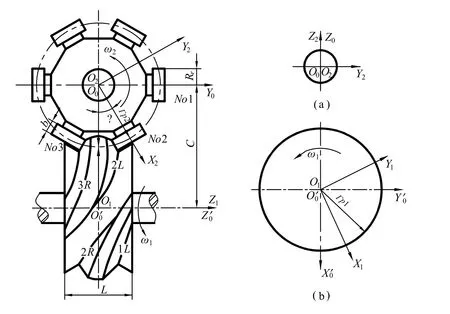
圖1 弧面分度凸輪機構的坐標系

各坐標系均用右手直角坐標系，其中：

（1） O0X0Y0Z0——與機架相連的定坐標系；

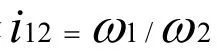
（3） O1X1Y1Z1——與凸輪1 相連的動坐標系；

（4） O2X2Y2Z2——與轉盤2 相連的動坐標系。

在圖1所示坐標系下可得到公軛接觸點K2（K1、K2分別為凸輪與轉盤滾子圓柱面的公軛接觸點）在坐標系O2X2Y2Z2中的坐標

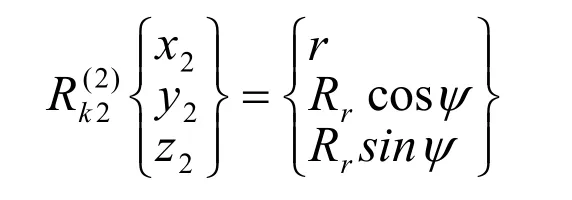
式中 r 、Ψ —— 滾子圓柱形工作面的方程參數；

Rr—— 滾子半徑。

凸輪與滾子的共軛接觸方程

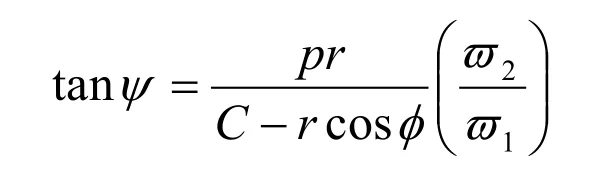
式中 φ ——滾子的位置角；

P ——凸輪的旋向系數，左旋為+1，右旋為-1；

C——凸輪與分度盤的中心距。

通過坐標變換得凸輪工作廓面在坐標系O1X1Y1Z1方程如下

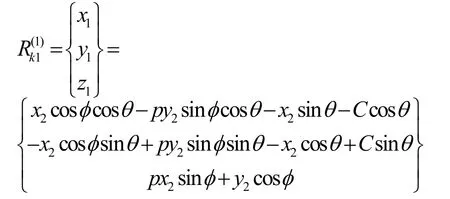
式中 φ——滾子位置角

φ = φ0+ pφi

式中0φ ——滾子的起始位置角

iφ ——滾子的角位移，ifSφ φ= ，S 是所選運動規律的量綱，fφ 轉盤分度期轉位角，iφ 恒取絕對值，0 ≤ φi≤φf。

圖中的1L、2L；2R、3R 分別為凸輪分度期工作廓面，L 面為槽左側脊的右側，R 面為槽右側脊的左側。

1.2 設計計算步驟

在上面公式的基礎之上，可得到凸輪廓面點的計算步驟如下：

（1） 按選定的運動規律由每一凸輪轉角θ求得轉盤相應的角位移iφ 和角速度比（2ω /1ω ），求得棍子的位置角φ。一般取θ ＝1°～2°為一個計算步長。

（2） 選定中心距C 后，把求得的φ 和2ω /1ω 帶入共軛接觸方程，得到每個θ 滾子圓柱面上共軛接觸點的曲面參數r 和ψ 間的制約關系。

（3） 每個θ 時設定一系列的r 值，由上述的制約關系求得相應的ψ ，同一個r 有兩個ψ ，ψ ≤90°用于凸輪輪廓R，ψ ≥180°用于凸輪輪廓L。

（4） 把同一θ 時r 和ψ 的每組對應值代入 輥子的坐標方程中，即可求得滾子圓柱面上共軛接觸點的坐標X2、Y2、Z2。

（5） 把上述每一θ 時求得的φ 和X2、Y2、 Z2帶入凸輪坐標方程式，即得到相應的凸輪工作輪廓的三維坐標值X1、Y1、Z1。

（6） 當凸輪轉角θ ＝fθ →360°，轉盤停歇，故θ=0 和θ ＝fθ 時的X1、Y1、Z1即為凸輪定位環面的三維坐標值。

1.3 計算實例

本文依據上述步驟，以表1給定條件采用VC++語言編程，來計算單頭8工位弧面分度凸輪工作廓面點(分度部分)的坐標。

表1 弧面分度凸輪的給定參數

圖2 是計算1L 廓面的程序流程圖。

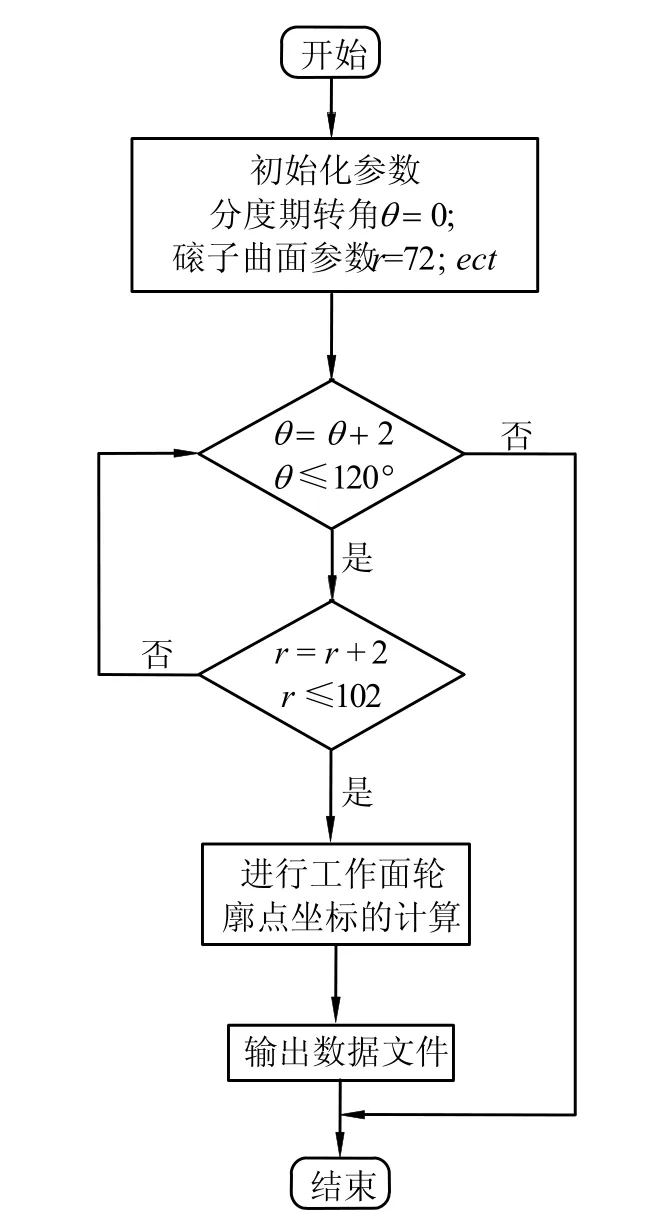
圖2 計算廓面點的程序流程圖

表2 是曲面1L 廓面的部分三維坐標數據，同理可得曲面2L、2R、3R 的廓面坐標。

2 三維模型的建立

Imageware是美國UGS公司出品的的逆向工程軟件，特別適于構造復雜曲面。它可以接受三坐標測量儀器測出的模型表面點陣數據、ASCII、*.dat等多種類型，因此可以將VC計算出的數據保存為文本文件，直接導入Imageware 中，或以*.dat數據直接導入，得到點云如圖3所示，然后由點云擬合成曲面。

為了便于后續設計仿真及加工，有必要生成弧面分度凸輪的實體模型。所以在這里選用UG軟件，Imageware 是UG 軟件中專門為逆向工程設計的模塊，兩個軟件在曲面構造原理上非常類似，通過Imageware 生成的工作曲面，可以直接以*.imw 等文件直接導入UG，如圖4 所示，其余曲面可在此基礎上采用“掃掠”等命令生成，縫和后自動生成實體，最后求并得到凸輪實體模型如圖5(a)所示，圖5(b)是弧面分度凸輪機構裝配圖。

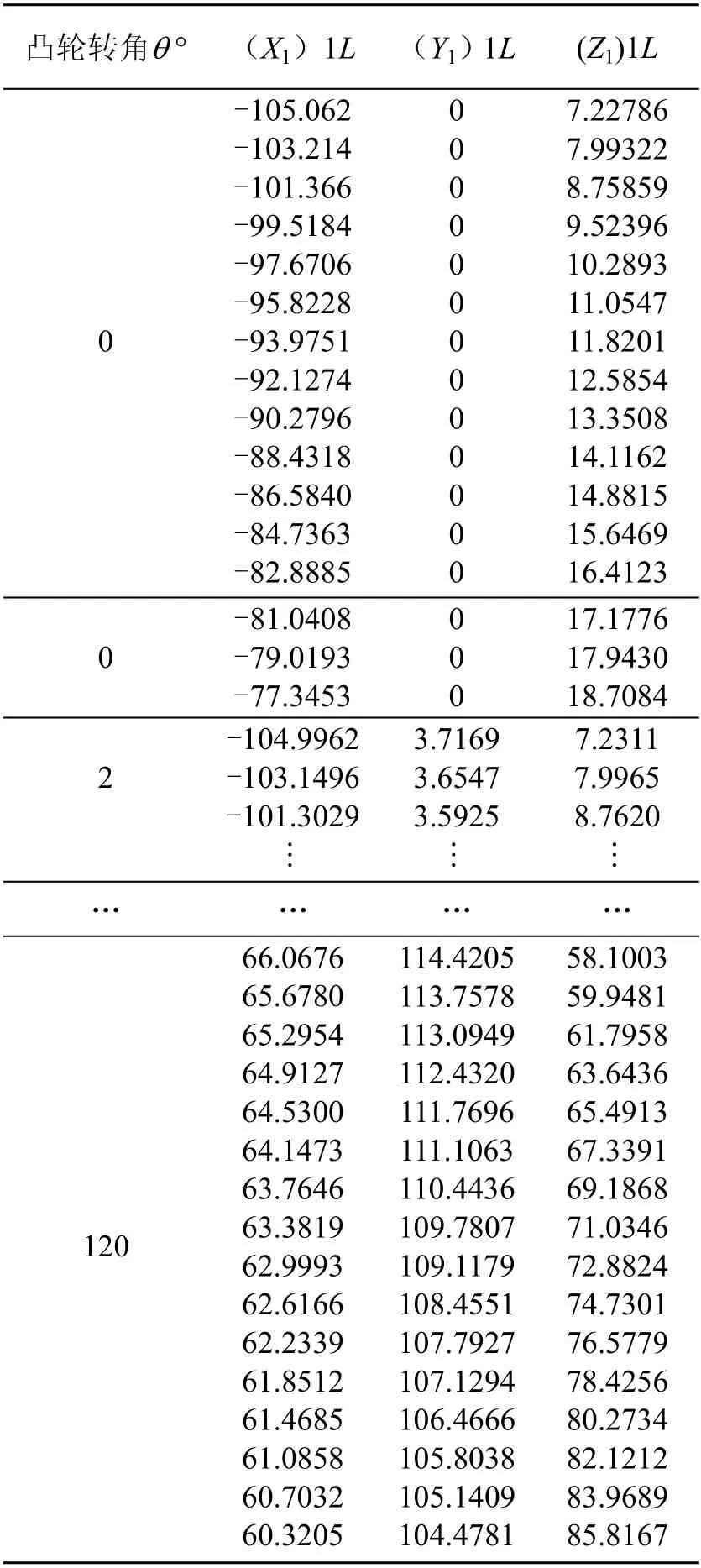
表2 曲面1L 的部分三維坐標數據

圖3 Imageware 中的點數據

圖4 導入UG 中的曲面

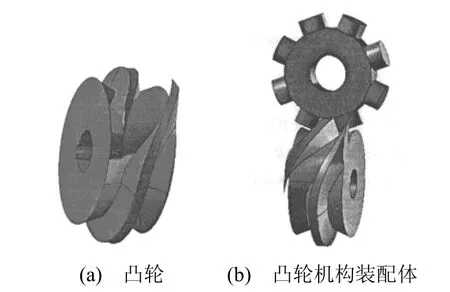
圖5 UG 下弧面分度凸輪

3 結 論

這里用VC++計算弧面分度凸輪的點云坐標，然后用Imageware軟件生成曲面，最終在UG下生成弧面分度凸輪的實體模型，這樣把逆向工程軟件和目前流行的三維繪圖相結合，減少了不必要的軟件開發工作，而且避免了由廓面數據點直接進入UG，而受UG讀入行數限制要縫合曲面的過程[4-5]，提高了工作曲面的建模精度（逆向工程軟件由點云擬合曲面的精度可達0.01mm）。同時由三維繪圖軟件構造出弧面分度凸輪及其裝配體的三維實體模型，補充了逆向工程軟件只能生成曲面模型的不足[6]，為弧面分度凸輪的虛擬設計和虛擬加工提供有效參考，也為后續參數化設計及后續先進加工技術（如：快速原形技術等）奠定基礎。

[1] 尹明富, 褚金奎, 呂傳毅. 鼓形滾子弧面分度凸輪廓面設計[J]. 機械設計, 2002, 19(2)： 50-52.

[2] 袁恩會, 張 淳, 董繼先. 弧面分度凸輪輪廓曲面在計算機上的生成[J]. 西北輕工業學院學報, 2001, 19(1)： 41-43.

[3] 吳文山, 王 莉, 周林航, 等. 基于UG 軟件的弧面分度凸輪機構的造型理論與設計[J]. 輕工機械, 2007, 25(4)： 47-50.

[4] 張高峰, 楊世平, 陳華章, 等. 弧面分度凸輪的三維CAD[J]. 機械傳動, 2003, 27(6)： 38-40.

[5] 葛文杰, 張王全. 基于Pro/ E 的弧面分度凸輪機構參數化設計與仿真[J]. 機械設計, 2005, 22(1)： 11-14.

[6] 梁延德, 宋麗娟. 弧面分度凸輪的三維建模[J]. 機械設計與制造, 2006, (8)： 142-143.