斜對(duì)稱(chēng)面檢測(cè)在二次曲面體中的應(yīng)用

王 翔， 丁運(yùn)亮， 李 靜

（1. 南京航空航天大學(xué)航空宇航學(xué)院，江蘇 南京 210016； 2. 南京航空航天大學(xué)自動(dòng)化學(xué)院，江蘇 南京 210016）

在從二維投影還原三維實(shí)體的過(guò)程中存在許多重要的幾何特征約束，對(duì)稱(chēng)就是其中的一 個(gè)[1]。對(duì)稱(chēng)將三維的自由度降低到二維；可以避免重復(fù)約束，因而大大降低了三維重建的難度，此外，對(duì)稱(chēng)還可以克服圖素間的遮擋和互疊問(wèn)題，即可以通過(guò)尋找對(duì)稱(chēng)面來(lái)恢復(fù)被遮擋部分的實(shí)體。因此，對(duì)稱(chēng)問(wèn)題具有很高的研究?jī)r(jià)值。

當(dāng)觀察者從非投影方向觀察對(duì)稱(chēng)時(shí)，便產(chǎn)生了斜對(duì)稱(chēng)，圖1 中就是幾個(gè)斜對(duì)稱(chēng)的例子，由于大多數(shù)情況下（除正投影外）視角均同投影方向有一定的夾角，因而斜對(duì)稱(chēng)是普遍存在的。由于斜對(duì)稱(chēng)是三維世界中的真實(shí)對(duì)稱(chēng)在二維情況下的反映，這就將三維中對(duì)稱(chēng)檢測(cè)轉(zhuǎn)化成了二維圖形下的斜對(duì)稱(chēng)檢測(cè)。

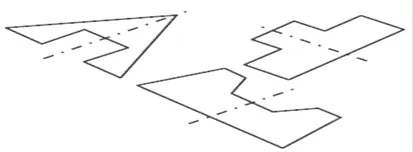
圖1 斜對(duì)稱(chēng)示例

在斜對(duì)稱(chēng)檢測(cè)方面，許多人進(jìn)行了大量的研究。Oh[2]和Yip[3]采用Hough 變換的方法進(jìn)行斜對(duì)稱(chēng)檢測(cè)，該方法能夠在干擾點(diǎn)存在以及圖形封閉的情況下進(jìn)行點(diǎn)和曲線的對(duì)稱(chēng)檢測(cè)，算法繁瑣。Shen[4]采用仿射不變特征向量法，通過(guò)一組仿射不變特征向量來(lái)描述圖形的幾何邊界，最終歸結(jié)為通過(guò)求解相似矩陣來(lái)尋找線段（對(duì)稱(chēng)軸）的問(wèn)題。算法復(fù)雜度為O(n2)，其中n 是為計(jì)算面積而在邊界上取的特征點(diǎn)數(shù)。算法效率有很大提高但是僅限于二維。Yip[5]采用橢圓傅立葉變換描述符對(duì)平行投影下的斜對(duì)稱(chēng)進(jìn)行檢測(cè)。該算法對(duì)于幾何實(shí)體的投影方向要求過(guò)于嚴(yán)苛，且不允許有遮擋情況存在。Lipson 和Shpitalni 提出了一種簡(jiǎn)便有效的檢測(cè)方法，通過(guò)計(jì)算最大權(quán)值系數(shù)來(lái)尋找對(duì)稱(chēng)軸，該算法仍然只適用于2D，無(wú)法檢測(cè)3D 的斜對(duì)稱(chēng)面。

Zabrodsky[6]將對(duì)稱(chēng)距離引入到了對(duì)稱(chēng)檢測(cè)中，其將對(duì)稱(chēng)距離定義為把某一實(shí)體變換到對(duì)稱(chēng)位置所需移動(dòng)的最小距離，其計(jì)算方法是取原物體所有的特征點(diǎn)在對(duì)稱(chēng)變換中移動(dòng)距離的平方的均值，理論上該方法能夠解決3D 空間中的對(duì)稱(chēng)檢測(cè)問(wèn)題，但是龐大的計(jì)算量使其無(wú)法處理復(fù)雜的模型。

Sugimoto[7]提出了自底向上的對(duì)稱(chēng)檢測(cè)方法，通過(guò)對(duì)低維圖素包括直線和曲線的斜對(duì)稱(chēng)軸檢測(cè)來(lái)實(shí)現(xiàn)高維圖形的斜對(duì)稱(chēng)檢測(cè)，該算法能夠處理圖素的遮擋和隱藏情況。但是，在曲線檢測(cè)部分只給出了橢圓的斜對(duì)稱(chēng)軸檢測(cè)方法，在此基礎(chǔ)上，本文將其擴(kuò)展并給出了任意二次曲線的斜對(duì)稱(chēng)軸檢測(cè)方法。

在三維實(shí)體斜對(duì)稱(chēng)面檢測(cè)方面，Zou[8]從點(diǎn)線面的拓?fù)潢P(guān)系入手，提出了平面體的斜對(duì)稱(chēng)面檢測(cè)方法，但算法覆蓋域僅限于平面體，無(wú)法處理二次曲面體。之所以二次曲面體的斜對(duì)稱(chēng)檢測(cè)最為復(fù)雜，是因?yàn)槿S空間對(duì)稱(chēng)面檢測(cè)歸根到底還是通過(guò)平面內(nèi)的斜對(duì)稱(chēng)軸檢測(cè)來(lái)實(shí)現(xiàn)的，以往的平面斜對(duì)稱(chēng)軸檢測(cè)算法最多給出了橢圓線的檢測(cè)，而對(duì)于像雙曲線、拋物線等復(fù)雜的二次曲線則沒(méi)有相應(yīng)的檢測(cè)方法。這樣，對(duì)于圓柱面等投影為圓或橢圓的規(guī)則曲面體，且放置位置固定時(shí)，可以用以往的算法加以解決，而對(duì)于其他二次曲面體或特殊擺放位置的實(shí)體以往算法則不能給出解決的方案。

本文從任意放置的空間二次曲線重建入手，通過(guò)計(jì)算曲線的參數(shù)表示來(lái)實(shí)現(xiàn)對(duì)曲線的類(lèi)型辨識(shí)，再通過(guò)擴(kuò)展改進(jìn)的斜對(duì)稱(chēng)軸檢測(cè)算法對(duì)所有面域圖素進(jìn)行斜對(duì)稱(chēng)軸檢測(cè)，最后剔除對(duì)稱(chēng)面內(nèi)曲線得到對(duì)稱(chēng)面多邊形的邊界，組裝成面即可得到二次曲面體的斜對(duì)稱(chēng)面。

1 面域提取

斜對(duì)稱(chēng)檢測(cè)是在獨(dú)立的圖素（直線或二次曲線）中進(jìn)行的，所以要將整個(gè)模型分割成獨(dú)立的面域。在這一步中需要輸入的是二維頂點(diǎn)的坐標(biāo)，輸出為一系列獨(dú)立的平面或曲面方程，生成的是平面或是曲面則由以下3 種情況決定[9]：

（1） 兩條不共線的直線邊決定一個(gè)平面；

（2） 一條直線邊和一條二次曲線邊相交，若直線邊位于曲線邊的支撐平面內(nèi)，則兩邊確定一個(gè)平面，否則對(duì)應(yīng)生成一個(gè)二次曲面；

（3） 兩條二次曲線邊相交，若兩曲線邊的支撐平面重合，則兩邊確定一個(gè)平面；否則對(duì)應(yīng)生成一個(gè)二次曲面。

使用極左鄰邊搜索法[10]即可提取所有表面上的閉環(huán)，根據(jù)相互間的位置關(guān)系如包含或分離確定內(nèi)環(huán)或外環(huán)。所有外環(huán)和內(nèi)環(huán)間的部分即構(gòu)成一個(gè)面域（見(jiàn)圖2）。

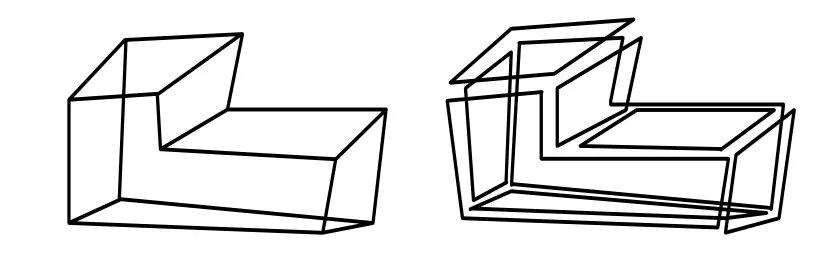
圖2 面域分割

2 預(yù)處理

提取得到的面域是一個(gè)個(gè)獨(dú)立的、閉合的多邊形，無(wú)法直接對(duì)其進(jìn)行對(duì)稱(chēng)檢測(cè)，因此首先要進(jìn)行一些預(yù)處理工作，其中主要包括圖形的分 割[11]和曲線的參數(shù)表達(dá)式求解。圖形經(jīng)分割后得到的圖素包括線段和曲線是斜對(duì)稱(chēng)軸檢測(cè)算法的直接作用對(duì)象，被打斷的圖素只是在連接關(guān)系上發(fā)生了改變，而其坐標(biāo)位置和幾何拓?fù)潢P(guān)系并未改變。不同的曲線類(lèi)型對(duì)應(yīng)的檢測(cè)算法也不相同，因此在檢測(cè)前要對(duì)得到的曲線進(jìn)行類(lèi)別辨識(shí)，本文則是通過(guò)求解曲線的幾何參數(shù)表達(dá)式來(lái)確定曲線的類(lèi)型。

2.1 圖形分割

將第一步提取的面域進(jìn)行分割處理，分割位置為輪廓線段的交點(diǎn)、端點(diǎn)以及曲線的極值點(diǎn)和拐點(diǎn)。相應(yīng)的判定方法是：交點(diǎn)處線段的連接度大于2；端點(diǎn)處的曲率有急劇的變化；極值點(diǎn)處曲率正負(fù)發(fā)生改變；拐點(diǎn)則是曲率從零值變?yōu)榉橇阒怠?/p>

分割后的圖素經(jīng)過(guò)曲率檢驗(yàn)后被分為直線和曲線兩大類(lèi)。而經(jīng)過(guò)下一步的曲線參數(shù)表達(dá)式求解之后，曲線將進(jìn)一步被劃分為橢圓、雙曲線和拋物線等。

2.2 投影曲線參數(shù)表達(dá)式求解

在計(jì)算機(jī)的幾何實(shí)體表示方法中，二次曲線在二維坐標(biāo)下一般有參數(shù)表達(dá)和隱式表達(dá)兩種表達(dá)方法。因參數(shù)表達(dá)法具有直觀簡(jiǎn)潔的特點(diǎn)，故通常采用更多的是這種表達(dá)方法，參數(shù)表達(dá)法首先需要明確二次曲線的類(lèi)型，然而在三維重建的問(wèn)題描述中，投影視圖中的曲線類(lèi)型是未知量，并且很難用模式識(shí)別的方法獲得其幾何參數(shù)。基于以上考慮，本文首先采用“五點(diǎn)法”[10]從視圖投影曲線直接構(gòu)造其一般代數(shù)表達(dá)式，然后采用解析法將得到的代數(shù)表達(dá)式轉(zhuǎn)換成相應(yīng)類(lèi)型的幾何參數(shù)表達(dá)式，為下一步的斜對(duì)稱(chēng)軸檢測(cè)做準(zhǔn)備。

2.2.1 “五點(diǎn)法”構(gòu)造投影曲線代數(shù)表達(dá)式

平面二次曲線的一般代數(shù)表達(dá)式為

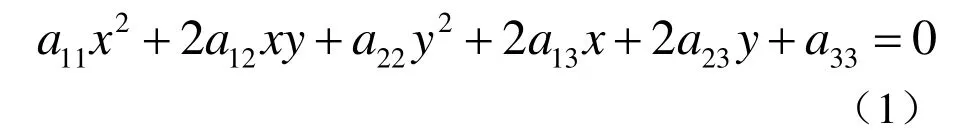
根據(jù)定理“給定五點(diǎn)，其中任意三點(diǎn)不共線，那么可以唯一確定一條二次曲線。”在投影曲線 上任意選取滿足要求的 5 個(gè)點(diǎn) Pi( xi, yi) ( i= 1,2,… , 5)，則曲線的代數(shù)方程（1）的系數(shù) 可以通過(guò)求解方程組

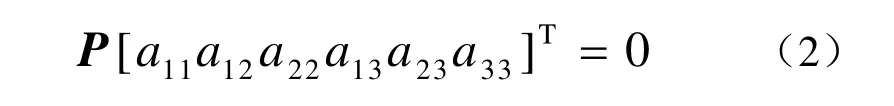
確定。其中

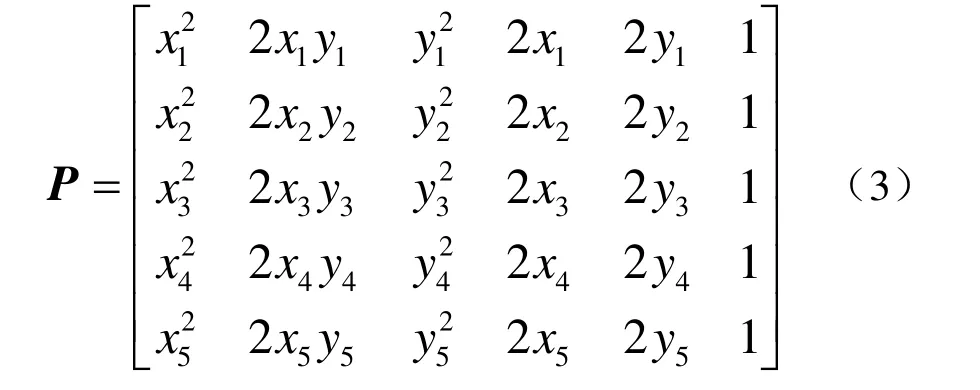
令點(diǎn)對(duì) ( pv1, pv2)、( ph1, ph2)、( pw1, pw2)分別表示主、俯、側(cè)視圖中的兩投影節(jié)點(diǎn)，以S ( pv1, pv2)、 S ( ph1, ph2)、 S ( pw1, pw2)分別表 示各視圖中的兩投影節(jié)點(diǎn)間存在的連接線段。這 樣，應(yīng)用“五點(diǎn)法”，分別由點(diǎn) pvi∈S ( pv1, pv2)、 phi∈S ( ph1, ph2)、pwi∈S ( pw1, pw2) ( i= 1,2,… , 5)可構(gòu)造出相應(yīng)的連接線段S ( pv1, pv2)、 S ( ph1, ph2)、 S ( pw1, pw2)的代數(shù) 表達(dá)式。

2.2.2 參數(shù)表示轉(zhuǎn)換

轉(zhuǎn)換后得到的曲線參數(shù)：

（1） 曲線的方向角θ

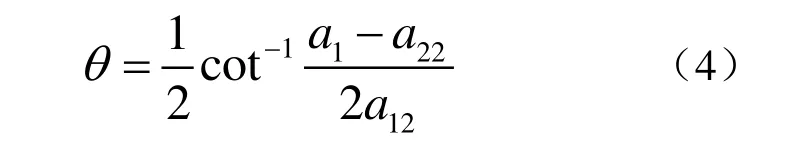
（2） 中心型二次曲線（橢圓、雙曲線）的中心 ( x0, y0)

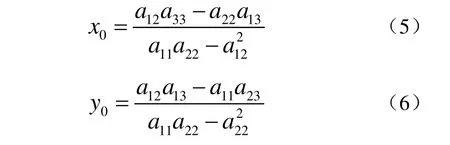
（3） 中心型二次曲線的長(zhǎng)短軸 },{ ba 橢圓

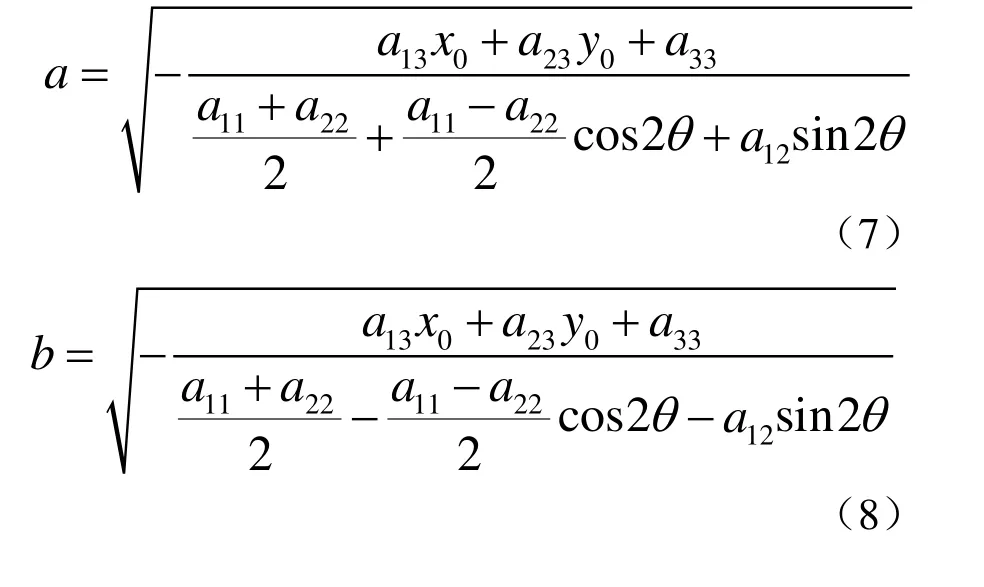
雙曲線

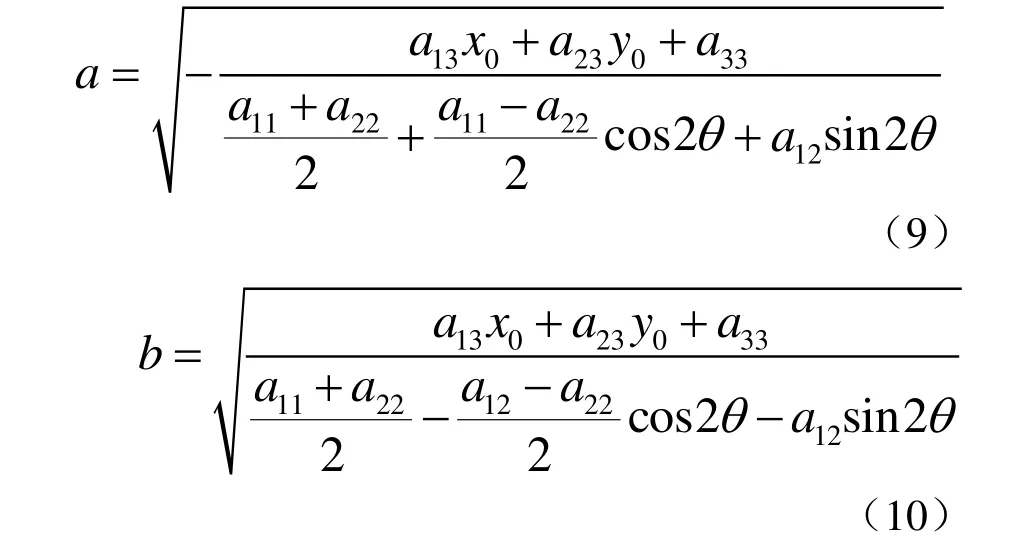
（4） 無(wú)心二次曲線（拋物線）的焦距和頂點(diǎn)坐標(biāo)

焦距

所有數(shù)據(jù)采用SPSS 24.0統(tǒng)計(jì)軟件進(jìn)行處理，所有檢驗(yàn)均為雙側(cè)檢驗(yàn)，P＜0.05表示差異有統(tǒng)計(jì)學(xué)意義。計(jì)量資料采用（±s）進(jìn)行統(tǒng)計(jì)描述，兩組間比較采用獨(dú)立樣本t檢驗(yàn)，方差不齊，采用t＇檢驗(yàn)，多組間比較采用單因素方差分析（F檢驗(yàn)）。計(jì)數(shù)資料采用率和頻數(shù)進(jìn)行統(tǒng)計(jì)描述，率的比較采用χ2檢驗(yàn)。尿酸與血壓、血糖等指標(biāo)的相關(guān)分析采用簡(jiǎn)單相關(guān)分析，因各指標(biāo)之間也相互關(guān)聯(lián)，為排除各因素之間的影響，故將尿酸與各指標(biāo)在簡(jiǎn)單相關(guān)分析后再控制其他因素進(jìn)行偏相關(guān)分析，如尿酸和身體質(zhì)量指數(shù)進(jìn)行偏相關(guān)分析時(shí)，控制因素為收縮壓、舒張壓、空腹血糖、甘油三酯、總膽固醇、高密度脂蛋白膽固醇、低密度脂蛋白膽固醇，依此類(lèi)推。

其中

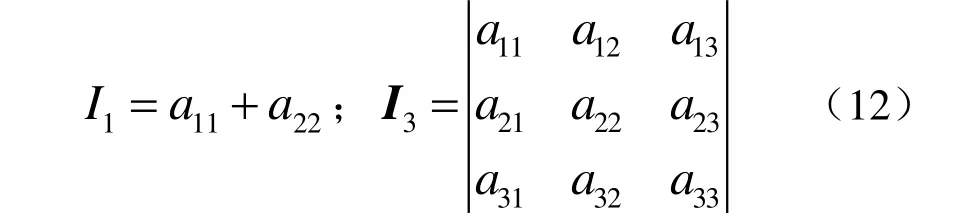
頂點(diǎn)坐標(biāo) ( x0, y0)

其中

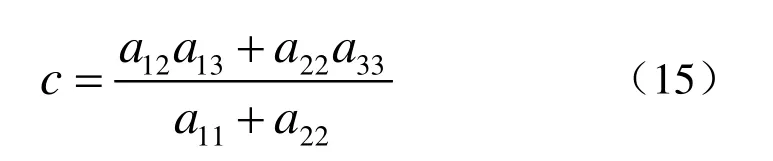
通過(guò)以上方法得到曲線的參數(shù)表達(dá)式以后，也就得到了曲線的類(lèi)型以及相應(yīng)的幾何參數(shù)，將曲線類(lèi)型和其對(duì)應(yīng)參數(shù)建立數(shù)據(jù)鏈表以備后續(xù)的對(duì)稱(chēng)檢驗(yàn)算法使用。

3 斜對(duì)稱(chēng)軸檢測(cè)

Kanade[13]最早給出了斜對(duì)稱(chēng)的定義：斜對(duì)稱(chēng)是實(shí)際的對(duì)稱(chēng)性在投影到圖象平面時(shí)產(chǎn)生的，即在2D 圖形中反映的3D 世界中的真實(shí)對(duì)稱(chēng)。斜對(duì)稱(chēng)的3 個(gè)基本參數(shù)為對(duì)稱(chēng)軸方向角、橫斷線方相角以及對(duì)稱(chēng)軸位置。

平面內(nèi)的斜對(duì)稱(chēng)軸檢測(cè)情況一共分為4 種：① 一條曲線；② 一對(duì)曲線；③ 一對(duì)直線和一條直線；④ 兩對(duì)直線。針對(duì)第①、③、④種情況已有較成熟的算法，在此不再累述，本文提出的改進(jìn)算法是針對(duì)第②種情況，Sugimoto 的算法只給出了曲線是橢圓的情況，在這里給出其他二次曲線的檢測(cè)方法。

3.1 拋物線以及雙曲線的斜對(duì)稱(chēng)軸檢測(cè)

對(duì)稱(chēng)軸的位置大體分為兩種情況：一種是位于兩拋物線中間，一種是貫穿兩拋物線。對(duì)于第一種情況，檢測(cè)算法為：

（1） 連接兩拋物線的焦點(diǎn)1P 和2P ，并取線段1P2P 的中點(diǎn) 0M ，線段1P2P 即為候選橫斷線；

（2） 在拋物線1 上取一系列點(diǎn)ia ，過(guò)ia 做線段1P2P 的平行線同拋物線2 交于點(diǎn)ib ，取線段iaib 的中點(diǎn) iM ，擬合點(diǎn) iM （i=0,1,2,…）即得到斜對(duì)稱(chēng)軸syL 。如圖3 所示。

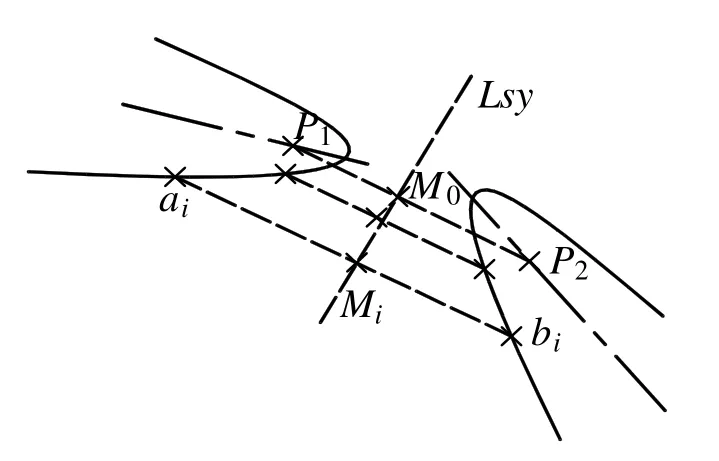
圖3 對(duì)稱(chēng)軸位于兩曲線中間

對(duì)于第二種情況，檢測(cè)算法為：

這種情況下只有一種對(duì)稱(chēng)的可能即對(duì)稱(chēng)軸為兩拋物線焦點(diǎn)的連線。因此，只需連接兩焦點(diǎn)即可得到斜對(duì)稱(chēng)軸。如圖4 所示。

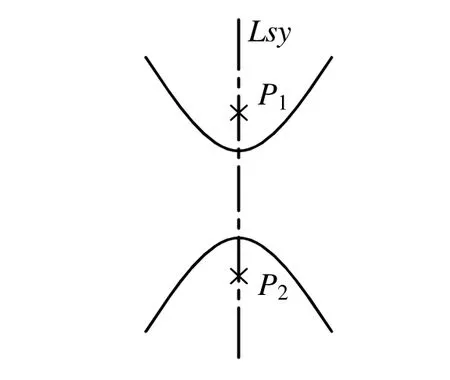
圖4 對(duì)稱(chēng)軸穿過(guò)兩曲線

4 斜對(duì)稱(chēng)面的構(gòu)造

4.1 尋找對(duì)稱(chēng)面多邊形的邊

如果在一個(gè)實(shí)體的平面投影中存在斜對(duì)稱(chēng)，那么一定可以找到一個(gè)或多個(gè)斜對(duì)稱(chēng)平面，且這些斜對(duì)稱(chēng)平面一定同實(shí)體的邊界或頂點(diǎn)相交，即斜對(duì)稱(chēng)平面在實(shí)體內(nèi)為一個(gè)多邊形（見(jiàn)圖5）。因此，如果找到該對(duì)稱(chēng)平面同實(shí)體的所有交線，就找到了該多邊形的所有邊，從而就得到了斜對(duì)稱(chēng)平面。Zou[8]的算法是針對(duì)平面體的，因此得到的交點(diǎn)要么是實(shí)體的頂點(diǎn)，要么是對(duì)應(yīng)邊的中點(diǎn)，并且對(duì)稱(chēng)多邊形的邊均為直線段，本文將實(shí)體范圍擴(kuò)展到了二次曲面體，因此斜對(duì)稱(chēng)面也就相應(yīng)地?cái)U(kuò)展到了曲邊多邊形。

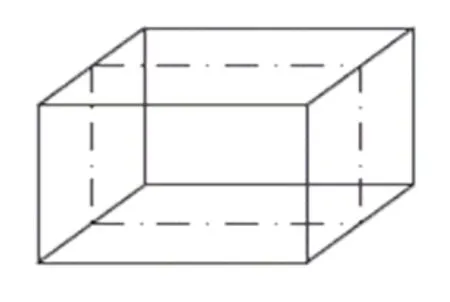
圖5 實(shí)體中的斜對(duì)稱(chēng)面

考慮到對(duì)稱(chēng)面多邊形的邊要么是某平面的對(duì)稱(chēng)軸，要么是實(shí)體的一條真實(shí)邊。故把所有檢測(cè)到的對(duì)稱(chēng)軸連同實(shí)體的邊組成Axes 表，作為對(duì)稱(chēng)面多邊形的邊的候選。同時(shí)建立VertexPairs表、CurvePairs 表以及FacePairs 表分別存放對(duì)應(yīng)于對(duì)稱(chēng)軸Axes 對(duì)稱(chēng)的點(diǎn)對(duì)、曲線邊對(duì)（也包括直線邊）以及面域?qū)Α?/p>

如圖6 所示，從Axes 表中取出一條邊 iaxes ,假定其中一對(duì)對(duì)稱(chēng)邊為1l 和1l′，1f 和1f′則是分別同它們相鄰的面域，如果1f 和1f′中所有的邊界曲線均關(guān)于軸 iaxes 對(duì)稱(chēng)，那么面域1f 同1f′關(guān)于軸 iaxes 對(duì)稱(chēng)，相應(yīng)地把1f 和1f′中所有的邊放入 CurvePairs 表中，所有的頂點(diǎn)放入VertexPairs 表 中，把1f 和1f′放入FacePairs 表中，接著選取下一組對(duì)稱(chēng)邊，重復(fù)上述過(guò)程，如圖中的曲線對(duì)2l和，檢測(cè)到與它們相鄰的斜對(duì)稱(chēng)面域?yàn)?f2和，依次類(lèi)推，當(dāng)同CurvePairs 表中的所有元 素相鄰的面域均能在FacePairs 表中找到時(shí)，表明滿足斜對(duì)稱(chēng)關(guān)系，即該對(duì)稱(chēng)軸位于對(duì)稱(chēng)面多邊形內(nèi)。下面是一些性質(zhì)定理，用于算法中錯(cuò)誤情況的判定，能夠有效地提高算法效率。

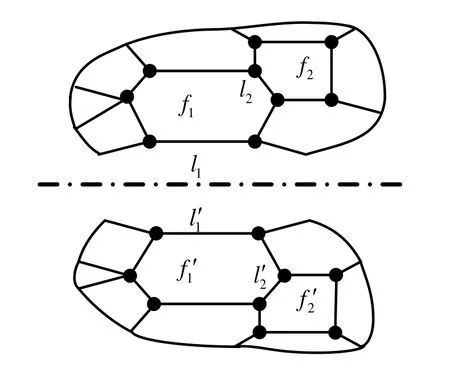
圖6 對(duì)稱(chēng)的點(diǎn)、線、面對(duì)

性質(zhì)定理1 某一實(shí)體關(guān)于一平面呈斜對(duì)稱(chēng)時(shí)，該實(shí)體的所有表面均應(yīng)出現(xiàn)在FacePairs 表中，否則說(shuō)明該實(shí)體無(wú)斜對(duì)稱(chēng)性。

性質(zhì)定理2 如果在FacePairs 表中出現(xiàn)了兩個(gè)相同的面域，則該面域中一定包含著對(duì)稱(chēng)平面多邊形的一條邊。

性質(zhì)定理3 在FacePairs 表中的兩個(gè)面域相交于一條邊，那么該邊一定是對(duì)稱(chēng)平面多邊形的一條邊。

算法具體步驟如下：

（1） 把檢測(cè)到的所有面的對(duì)稱(chēng)軸以及實(shí)體的邊界曲線放入Axes 表中；

（2） 選取Axes 表中的一個(gè)對(duì)稱(chēng)軸，同時(shí)置VertexPairs 表、CurvePairs 表以及FacePairs表為空；

（3） 把找到的關(guān)于該對(duì)稱(chēng)軸的曲線對(duì)放入CurvePairs 表中；

（4） 按以下三步進(jìn)行：

1） 從CurvePairs 表中選擇一個(gè)新的曲線邊對(duì)，當(dāng)CurvePairs 表中所有曲線邊對(duì)均被處理完時(shí)，轉(zhuǎn)入步驟（5）；

2） 對(duì)于選中的曲線邊對(duì)，檢測(cè)其所有相鄰的面域，滿足對(duì)稱(chēng)關(guān)系的面域?qū)Ψ湃隖acePairs表中，相應(yīng)的邊和頂點(diǎn)存入CurvePairs 表和VertexPairs 表中；

3） 如果沒(méi)有任何相鄰面域滿足對(duì)稱(chēng)關(guān)系，則該軸不位于對(duì)稱(chēng)面多邊形內(nèi)，同時(shí)轉(zhuǎn)入步驟（5）；

（5） 如果所有同該軸相鄰的面域均能在FacePairs 表中找到時(shí)，說(shuō)明該軸位于對(duì)稱(chēng)面多邊形內(nèi)，并將其存入對(duì)稱(chēng)多邊形邊表中，否則刪除該軸，并轉(zhuǎn)入步驟（2）。

4.2 構(gòu)造對(duì)稱(chēng)面

上一步中找到的所有的位于對(duì)稱(chēng)面多邊形內(nèi)部的對(duì)稱(chēng)軸中既包含了對(duì)稱(chēng)面多邊形的邊，同時(shí)還有位于多邊形面內(nèi)的對(duì)稱(chēng)軸，而構(gòu)造對(duì)稱(chēng)面多邊形只需用到邊界上的直線和曲線，因此需要將位于面內(nèi)的直線和曲線去除。方法是利用邊界曲線同內(nèi)部曲線的拓?fù)湫再|(zhì)入手：邊界曲線的交點(diǎn)一定位于實(shí)體的邊或者面上；而內(nèi)部曲線的交點(diǎn)一定位于實(shí)體的內(nèi)部。具體判定準(zhǔn)則如下：

（1） 邊為直線情況

1） 如果兩直線的交點(diǎn)坐標(biāo)滿足實(shí)體邊或表面的方程，并且兩直線上的任意一內(nèi)點(diǎn)滿足實(shí)體的表面方程，那么這兩條直線均為對(duì)稱(chēng)面的邊，同時(shí)保留。

2） 如果兩直線的交點(diǎn)坐標(biāo)滿足實(shí)體邊或表面的方程，并且其中一條直線的內(nèi)點(diǎn)滿足實(shí)體的表面方程，那么該直線是對(duì)稱(chēng)面的邊，予以保留，另外一條內(nèi)點(diǎn)不滿足實(shí)體表面方程的直線則被去除。

3） 如果兩條直線的交點(diǎn)不滿足實(shí)體邊或表面的方程，即兩條直線均為內(nèi)部直線，同時(shí)被去除。

（2） 邊中含有曲線的情況

1） 由于作為對(duì)稱(chēng)面邊界的曲線一定是位于二次曲線面體的曲面部分，故其某一曲線的任意內(nèi)點(diǎn)坐標(biāo)均應(yīng)滿足曲面的參數(shù)方程，否則一定不是邊界曲線，去除之。

2） 同被檢測(cè)出的邊界曲線相交的直線，其直線的任意內(nèi)點(diǎn)坐標(biāo)一定要滿足實(shí)體的表面方程，否則被除去。

運(yùn)用極左鄰邊搜索法[10]提取生成對(duì)稱(chēng)面的方程，加上各個(gè)實(shí)體表面的方程約束便得到斜對(duì)稱(chēng)多邊形的方程。

5 結(jié)果及討論

圖7 中所示的紅線為邊界的平面為使用本算法檢測(cè)到的斜對(duì)稱(chēng)面，由于算法對(duì)于實(shí)體的擺放位置沒(méi)有要求，因而可以識(shí)別軸線任意放置的二次曲面體。

對(duì)稱(chēng)面的檢測(cè)對(duì)于三維重建有著十分重要的意義，利用檢測(cè)到的二次曲面體的對(duì)稱(chēng)面可以去除多余約束，方便地實(shí)現(xiàn)二次曲面實(shí)體的三維重建。

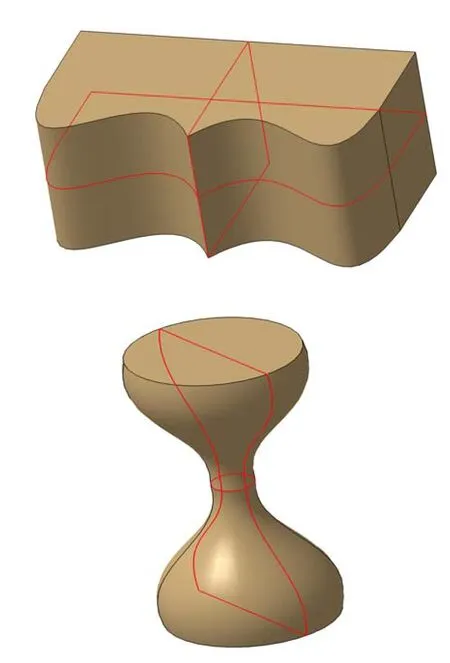
圖7 二次曲面體及其檢測(cè)到的斜對(duì)稱(chēng)面

[1] LIPSON H, SHPITALNI M. Optimization-based reconstruction of a 3D object from a single freehand line drawing [J]. Computer Aided Design, 1996, 28(8): 651-663.

[2] OH W G, ASADA M, TSUJI S. Model-based matching using skewed symmetry information [C]// Proc. Int'l Conf. Pattern Recognition, 1998: 1043-1045.

[3] YIP R HOUGH. A transform technique for the detection of reflectional symmetry and skew-symmetry [J]. Pattern Recognition Letters, 2000, 21: 117-130.

[4] SHEN D G, IP H H S, TEOH E K. Robust detection of skewed symmetries by combining local and semi-local affine invariants [J]. Pattern Recognition, 2001, 34: 1417-1428.

[5] YIP R K K, TAM P K S, LEUNG D N K. Application of elliptic Fourier Descriptors to symmetry detection under parallel projection [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1994, 16(3): 277-286.

[6] ZABRODSKY H. Computational aspects of pattern characterization-continuous symmetry [D]. Hebrew University, Jerusalem, Israel, 1993.

[7] SUGIMOTO K, TOMITA F. Detection of skewed-symmetrical shape [C]//Proceedings of the International Conference on Image Processing. Austin, Texas, USA, 1994: 696-700.

[8] Zou H L, Lee Y T. Skewed mirror symmetry detection from a 2D sketch of a 3D model [C]//Proceedings of the 3rd International Conference on Computer Graphics and Interactive Techniques in Australasia and South East Asia, 2005: 69-76.

[9] Zhang Aijun, Zhu Changqian, Xue Yong. Reconstruction of curvilinear 3D objects from orthographic views [J]. Journal of Computer Research and Development (in Chinese), 2002, 39 (11): 1423-1428.

[10] Kuo M H. Reconstruction of quadric surface solids from three-view engineering drawings [J]. Computer-Aided Design, 1998, 30(7): 517-527.

[11] Sugimoto K, Tomita F. Boundry segmentation by detection of corner, inflection, md transition points [C]// Proc. IEEE Workshop on Visualization and Machine Vision, 1994: 13-17.

[12] Lequette R. Automatic construction of curvilinear solid from wire-frame views [J]. Computer-Aided Design, 1988, 20(4): 171-180.

[13] KANADE T. Recovery of the three-dimensional shape of an object from a single view [J]. Artificial Intelligence, 1981, 17: 409-460.