自調勻整模糊控制系統設計及FPGA實現

朱耀麟，李蘭君，張 濤，王延年

（西安工程大學 電子信息學院，西安 710048）

自調勻整模糊控制系統設計及FPGA實現

朱耀麟，李蘭君，張 濤，王延年

（西安工程大學 電子信息學院，西安 710048）

針對自調勻整系統控制過程復雜、難以建立精確模型的特點，設計了基于現場調試經驗的模糊控制算法.為了提高控制性能，采用常規PID與模糊控制相結合的方法.在Altera公司提供的QuartusII開發環境中，利用原理圖設計和VHDL設計輸入相結合的方式，在FPGA上實現了模糊PID控制算法.根據仿真結果分析，該設計實現了模糊PID控制功能.

自調勻整；模糊控制；FPGA；模糊自整定PID控制器

自調勻整是一種用來控制紗條粗細不勻的自動調節裝置，它在現代紡織工業中有著極其重要的地位.該系統是一個強擾動（輸入棉條線密度不斷變化）、大延遲（勻整點到檢測點的延時）的定值（輸出棉條的線密度為一定值）系統[1].傳統的PID控制方法主要適用于線性控制過程，對于這種滯后比較嚴重的被控對象控制效果較差.由于自調勻整系統具有非線性、時變性、不確定性的特點，難以建立精確的數學模型，采用經典控制理論中的PI和PID控制規律很難獲得滿意的效果.而模糊控制不需要控制對象的精確數學模型，它是一種基于規則的控制，依據操作人員的控制經驗和專家知識，通過查表就可以得到控制量，實現簡單，控制效果好.模糊控制尤其適用于數學模型未知、復雜的非線性系統的控制.采用模糊推理的方法實現PID參數kp、ki、kd的在線自整定，不僅保持了常規PID控制系統原理簡單、使用方便、魯棒性較強等優點，而且具有更大的靈活性，整定性、控制精度更好，是目前較為先進的一種控制系統.分析表明，基于模糊控制與常規PID結合是提高控制性能的有效手段[2].姚杰等[3]分析了高速并條機短片段自調勻整裝置，開發出基于開環控制的、帶有雙自調因子與量化因子優化相結合的智能型模糊控制器.Yueyang guo[4]在梳棉機上運用一套通用可預測理論進行自調勻整，得出了控制模型.李洪興[5-6]從模糊控制的插值機理出發，揭示出模糊控制器的本質是某種插值器，并介紹了基于論域收縮的一類模糊控制器的設計思想.無論是梳棉機還是并條機，其靜態數學模型都比較簡單，但設計高質量的能適應高速的自調勻整系統，僅有靜態數學模型還遠遠不夠，必須建立能用于控制工程的動態模型.本文從勻整理論入手，結合現代計算機控制理論，主要研究自調勻整機構的實現方案和勻整控制理論，并應用理論設計一種在梳棉機上使用的自調勻整機構.

1 自調勻整系統的數學模型及傳統控制方法

自調勻整裝置按其控制形式可分為開環、閉環和混合環.混合環是開環和閉環的混合形式，它將快速反應的開環系統與中、低速反應的閉環系統有機結合起來，在控制機構上疊加兩方面檢測到的訊號，取長補短，使棉條的短中長片段均勻度得到改善.圖1為自調勻整混合環控制系統結構圖.

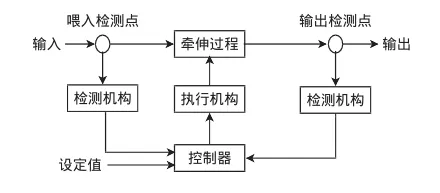
圖1 自調勻整混合環控制系統Fig.1 Hybrid loop autoleveller system

由梳棉機的特性，梳棉機的數學模型為[7]：

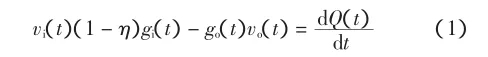
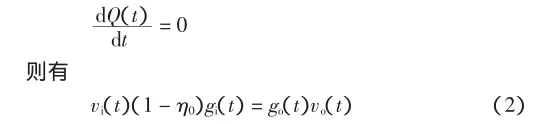
梳棉機自調勻整裝置的目的就是使輸出條子均勻，即go（t）=gos，gos為輸出生條線密度的設定值.由式（2）可得控制律為：

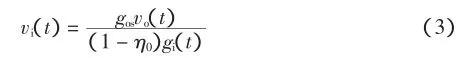
式中：η為落棉率；gi（t）為喂入棉層線密度（g/m）；go（t）為輸出生條線密度（g/m）；vi（t）為喂入棉層線速率（m/ s）；vo（t）為輸出棉層線速率（m/s）；Q（t）為梳棉機內纖維存量（g/m）.設落棉率不變為η0，且梳棉機內棉纖維存儲量基本不變，即

實際生產中很難精確檢測線密度的變化，通常在梳棉機上檢測到的是輸入棉層厚度和輸出棉條的粗細，然后通過調節羅拉的牽伸倍數達到使輸出棉條均勻的目的.自調勻整系統復雜，且由于落棉率等一些未知因素的影響，要得到精確的數學模型十分困難，且傳統的PID控制有慣性滯后的影響.因此，使用模糊理論對本系統進行控制是十分合適的.

2 自調勻整的模糊自整定PID算法

模糊自整定PID是在PID算法的基礎上，通過計算當前系統誤差e和誤差變化率ec，利用模糊控制規則進行模糊推理，查詢模糊矩陣表進行參數調整.模糊自整定PID控制器的離散表達形式如下[8]：

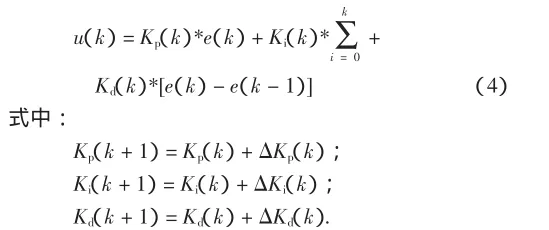
模糊自整定PID控制器以誤差e和誤差變化量ec作為輸入，可以滿足不同時刻的e和ec對PID參數自整定的要求.利用模糊控制規則在線對PID參數進行修改，便構成了自適應模糊PID控制器，其結構如圖2所示[9].

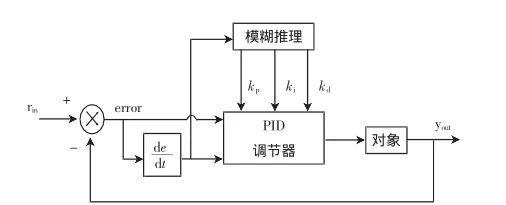
圖2 自適應模糊控制器結構Fig.2 Structure of fuzzy self-tuning PID controller

PID參數模糊自整定是找出PID的3個參數與e和ec之間的模糊關系，在運行中通過不斷檢測e和ec，根據模糊控制原理對3個參數進行在線修改，以滿足不同e和ec時對控制參數的不同要求，而使被控對象有良好的動、靜態性能.

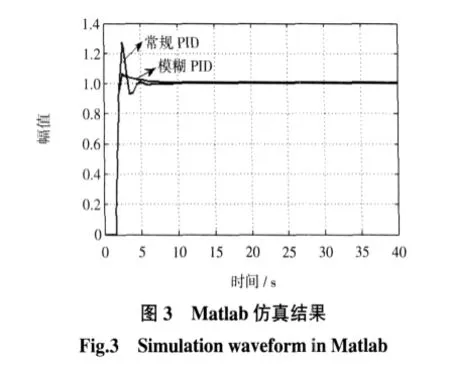
由圖3仿真結果可知，常規PID和模糊PID的響應速度、穩定性相當，但是常規PID的超調量為28%，而模糊PID的超調量只有7%，與常規PID相比，模糊PID的超調量更小.

3 模糊PID算法的FPGA實現

模糊控制策略較為理想的實現方式是基于硬件，因此，本文選擇FPGA實現模糊自整定PID算法.FPGA最明顯的優勢在于集成度高、體積小、功耗低、可靠性高、電路設計靈活.通過FPGA技術來實現模糊PID算法控制，把系統的硬件和軟件充分結合，可揚長避短，使其最大限度地發揮各自的優點，使得硬件的成本降到最低；同時保證了系統算法模塊的簡化，減少了處理器對算法的運算，提高了系統的運行速度，在復雜的控制系統中，可以大大地減輕處理器的負擔，為算法的優化提供可行的方式；大大降低了由于計算機故障對控制系統的影響，提高了控制模塊的可靠性.圖4為基于FPGA的模糊自整定PID控制器電路架構.

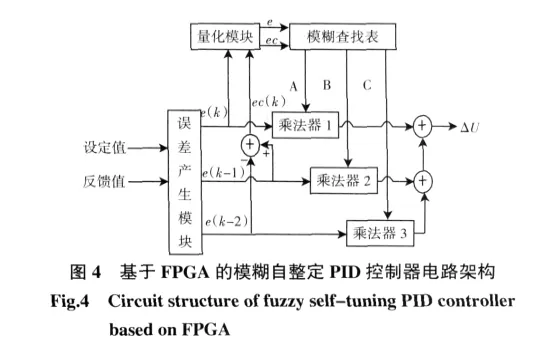
系統分為4個模塊：誤差產生模塊、量化模塊、模糊查找表模塊以及乘加模塊.誤差產生模塊生成誤差（設定值和反饋值的差值）和誤差變化率的精確值；量化模塊是將誤差和誤差變化率的精確值量化成為模糊值；該模糊值作為模糊查找表的輸入，經模糊查找表之后輸出PID參數的值，經乘加運算后輸出控制量U值.

3.1 誤差及誤差變化量模塊的設計

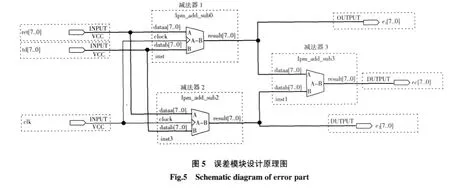
模糊PID算法的輸入是誤差及其誤差的變化率，誤差是設定值與反饋值的差值，根據前后兩次誤差量可以得出誤差變化率.在離散化論域中，將當前周期的誤差量與上一個周期的誤差量進行比較產生誤差變化量，利用誤差變化量的值來代替誤差變化率.本模塊的設計通過QuartusII模塊庫中的LPM_ADD_SUB來實現，但只采用了此模塊的減法功能[10].圖5為誤差模塊設計原理圖.

3.2 模糊量化等級模塊的設計

誤差和誤差變化量模塊輸出的是精確值，而模糊控制器的輸入必須是經過量化后的模糊值.因此，精確值需經模糊量化后才能作為模糊控制器的輸入.此模塊的基本思想是：首先將模糊論域范圍內輸入的精確量進行量化，使其符合論域范圍；將模糊論域按基本元素的不同分為若干段，每一段對應于一個論域中的基本元素.當輸入精確值落入某個論域范圍段時，經過模糊量化后，對應此精確量的輸出量即為此論域的基本元素值.本文中將誤差大小量化為7個等級，基本論域范圍為[-30，30]，量化因子為10，采用四舍五入的方法，將基本論域分為7段.利用QuartusII里LPM_COMPARE函數實現精確值與量化值的比較，量化后再通過一片74148對量化值進行編碼，使每一個量化值都對應一個編碼.假設誤差的精確值是12，此精確值在[5，15）的論域段，那么誤差的量化值就是1. ec和e的量化過程相同，表1為e/ec的量化地址.

表1 模糊量化后e/ec的量化地址Tab.1 Fuzzy address of e/ec

3.3 模糊查找表模塊

模糊查找表是模糊控制器的核心[11]，本文采用離線計算得到的控制表來代替模糊化運算、模糊推理和清晰化計算等一系列復雜的工作，而且在實際控制時在線運算量很少.這種離線計算、在線查表的方法大大提高了FPGA的工作效率，而且降低了編程難度.

Matlab的模糊邏輯工具箱提供了建立和測試模糊邏輯系統的一整套功能函數，包括定義語義變量及隸屬度函數、建立模糊推理規則、整個模糊推理系統的管理以及交互式地觀察模糊推理過程和推理結果.考慮到e和ec都是經過量化的值，即模糊輸入的論域是離散的，這就意味著輸入量e和ec的數目是有限的，可以在Matlab中建立該模糊邏輯函數的模型，把所有e和ec的組合輸入模糊推理模型里，求出在這些輸入下kp、ki和kd的值.為進一步降低計算復雜度，可設變量

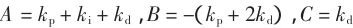
即對kp、ki和kd的值進行線性組合，可以制作出一份以e、ec為輸入，以A、B、C為輸出的控制表.其中高3位是誤差e的量化地址，低3位是誤差變化率ec的量化地址.將A、B、C表在QuartusII里制作成.mif文件，分別放入3個ROM里.那么在FPGA上要完成的工作就只剩下計算：

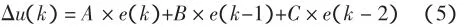
3.4 乘法模塊和加法模塊

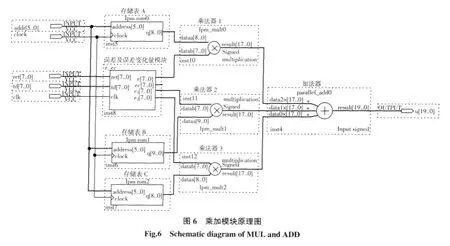
乘法模塊調用了函數庫里的LPM_MULT實現A與e（k）、B與e（k-1）、C與e（k-2）的相乘，然后調用parallel_add將3個值相加得到控制量Δu.圖6為乘加模塊原理圖.

3.5 系統頂層電路原理圖及其仿真

系統頂層電路原理圖如圖7所示.

取一組數據，令ret=21，td=30，那么誤差精確值e=-9，e1=-9，e2=-16，誤差變化量的精確值ec=7，精確值e屬于[5，15）論域段，其量化值是-1，量化編碼010.同理可知ec的量化編碼100.將e的量化編碼作為高3位，ec的量化編碼作為低3位，查表可知A=-110，B=219，C=-109，由（5）式計算可得U=763.仿

真結果如圖8所示.

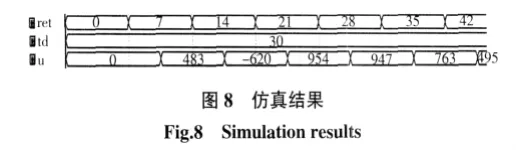
由圖8可以看出，仿真與計算結果相同，證明了系統整體設計的正確性，說明此種方法切實可行.

4 結束語

與傳統PID控制相比，模糊控制更適用于大滯后、非線性的復雜系統.因此，本文提出用模糊控制方法對自調勻整系統進行控制，使用Altera的FPGA設計實現了模糊自整定PID控制器，設計采用離線計算、在線查表的模糊自整定參數技術和增量式PID算法.仿真結果顯示，本設計既降低了FPGA的資源耗費，又改善了傳統PID控制器的控制性能，設計方案可行.

[1]郭月洋，陳瑞琪.棉紡設備自調勻整系統發展方向的探討[J].棉紡織技術，2002，30（5）：29-32.

[2]王化祥.一種新型模糊PID調節器的設計[J].自動化儀表，2000，21（5）：8-10.

[3] 姚 杰，葉國銘.新型開環自調勻整裝置的分析與設計[J].紡織學報，2005，26（3）：44-45.

[4] GUO Yueyang.Applying a generalized predictive control theory to a carding autoleveler[J].Textile Res J，2003，73（9）：755-761.

[5] 李洪興.Fuzzy控制的本質與一類高精度Fuzzy控制器的設計[J].控制理論與應用，1995，14（6）：868-872.

[6] LI Hongxing，CHEN C L Philip.Relationship between fuzzy controller and PID controller[J].Science in China:Series E，1999，42（2）：215-224.

[7] 曾光奇，胡均安，王 東，等.模糊控制理論與工程應用[M].武昌：華中科技大學出版社，2006.

[8] 謝仕宏.MATLABR2008控制系統動態仿真實例教程[M].北京：化學工業出版社，2009.

[9]劉金琨.先進PID控制MATLAB仿真[M].北京：電子工業出版社，2004.

[10]王軍偉.基于FPGA的模糊PID控制算法的研究及實現[D].杭州：浙江工業大學，2009.

[11]李昌武，彭良玉.模糊自整定PID控制器的FPGA實現[J].現代電子技術，2007，256（17）：116-121.

Design of fuzzy control system in autoleveller based on FPGA

ZHU Yao-lin，LI Lan-jun，ZHANG Tao，WANG Yan-nian
（Electronic Information College，Xi′an Polytechnic University，Xi′an 710048，China）

According to the speciality of complex controlling rule and difficult building of system model，a fuzzy controller based on experiences is designed.In order to improve control performance，the traditional PID is combined with fuzzy control method.The fuzzy PID control algorithm is implemented on FPGA by using the hierarchical modular design and combining the schematic design method with VHDL design method in the QuartusII development environment provided by Altera.According to the result of the simulation analysis，the control chip achieves the desired function of fuzzy PID control algorithm.

autoleveller；fuzzy control；FPGA；fuzzy self-tuning PID controller

TS103.113；TP29

A

1671－024X（2010）06－0063－05

2010-08-30

朱耀麟（1977—），男，博士，副教授，碩士生導師.

朱耀麟（1977—），男，博士，副教授，碩士生導師.E-mail：fz_zyl@126.com

·科研鑒定·