地層吸收對彈性參數的影響和疊前QAVO反演

張繁昌,李傳輝,吳國忱,王保麗

(中國石油大學 地球資源與信息學院,山東東營 257061)

0 前言

隨著油氣勘探重點由構造型油氣藏向巖性油氣藏、隱蔽油氣藏的轉移,地層對地震波的吸收衰減越來越引起地球物理工作者的重視。地震波在地下介質中傳播時的能量衰減分為二類:①與地震波傳播特性有關的衰減,包括球面擴散,散射及透射損失等,這部份能量在資料處理時已對其進行補償;②地層本身的本征衰減,即地層的吸收,這種介質本身所固有的吸收特性通常用固有品質因子Q來描述[1]。Q值與介質的結構、孔隙度,以及孔隙流體的性質密切相關,被認為是隱蔽油氣藏預測最為敏感、可靠的依據之一[2]。

目前,地震資料的解釋已進入以巖性解釋為主的階段,而巖石的彈性參數在巖性解釋中,扮演著非常重要的角色。當地層吸收嚴重時,就需要考慮吸收對巖石彈性參數帶來的影響[3]。例如對地層波阻抗、彈性阻抗的影響,以及由于吸收引起的AVO類型的改變等,這些影響將會直接關系到巖性解釋的準確性,因而研究地層吸收對巖石彈性參數的影響具有十分重要意義。

自Futter man把吸收衰減作為地層的基本特性以來,許多學者在地層吸收方面作了大量的研究:Tonn[4]曾對十多種地層吸收和品質因子計算方法作了比較;尹陳等人[5]利用二維粘彈性波動方程研究了地震波的吸收衰減特性;Koesoemadinata等[6]利用實驗室測量數據,建立了砂巖儲層物性參數(孔隙度、含水飽和度、泥質含量、有效地層壓力等)與地球物理參數(縱波速度Vp、橫波速度Vs、密度ρ、品質因子Q等)的經驗關系,并利用這些經驗關系由儲層物性參數來估算Q值。因此,綜合利用地層的品質因子和縱橫波信息進行儲層預測,可以進一步降低勘探風險。

作者在本文中從粘彈性介質的本構方程出發,推導了地層吸收對波阻抗值的影響,進而分析并討論了地層吸收對地震數據的AVO特征,以及彈性阻抗的影響,最后將地層品質因子Q融入到疊前彈性阻抗反演過程中,實現了地層品質因子與縱橫波阻抗參數的同時反演。

1 地層吸收對波阻抗的影響

地下介質對地震波的吸收通常用品質因子Q來衡量,品質因子越小,地層對地震波的吸收越嚴重。為了量化地層吸收對巖石彈性參數的影響,下面從粘彈性介質本構方程出發,來推導品質因子與波阻抗之間的關系。

在線性粘彈性介質的基本模型中,Kelvin-Voigt模型(見圖1(a))未考慮應力作用下應變的突然變化,也不能表示應力消失后的剩余應變;而Maxwell模型(見圖1(b))不具備蠕變特征;標準線性粘彈性模型(見圖1(c))彌補了前二者的不足[7],作者采用該粘彈性模型來討論吸收特性。

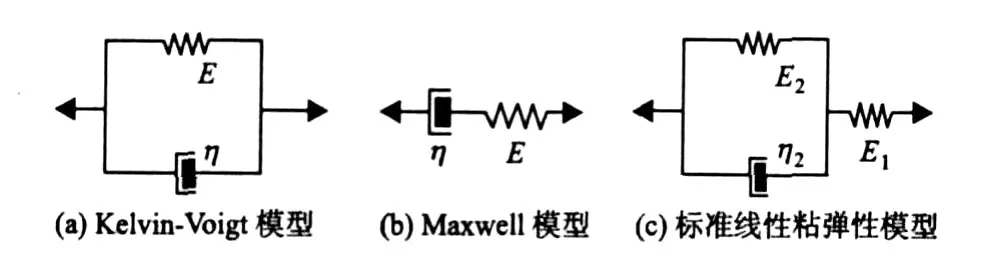
圖1 線性粘彈性介質基本模型Fig.1 Basic linear viscoelastic model

標準線性粘彈性模型的本構方程為[8]:

其中 E1和E2是彈性模量;η為粘性系數;σ為應力;ε為應變。

應力與應變的關系為σ=M(ω)ε,其中關于頻率ω的復模量M(ω)為:

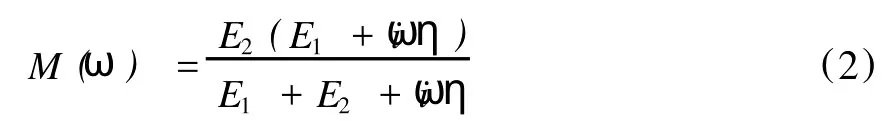
根據復模量,地層品質因子Q即可表示為:

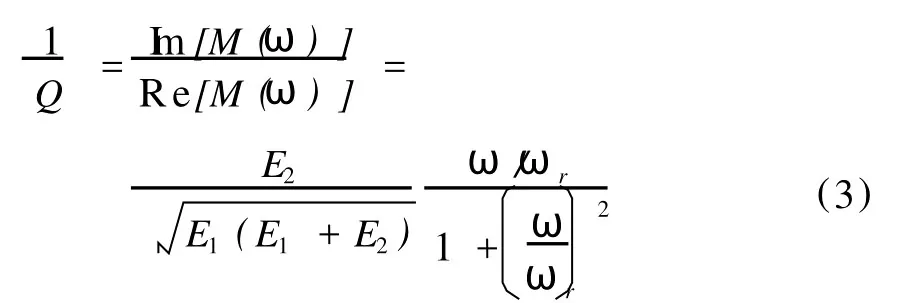
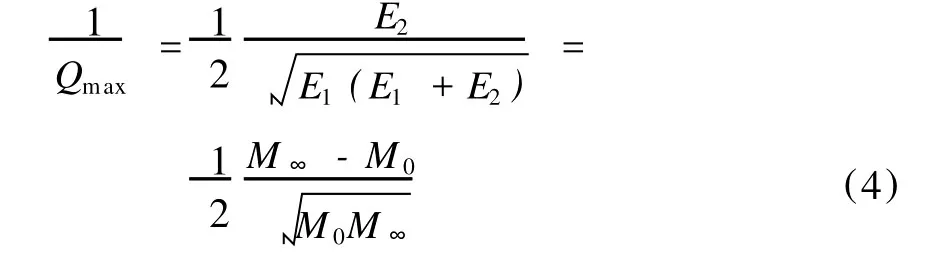
由式(3)得到最大衰減為:其中 M0、M∞分別是高頻、低頻極限下的模量。

為了使品質因子Q與模量之間的關系更明顯,對式(4)進行變換得:

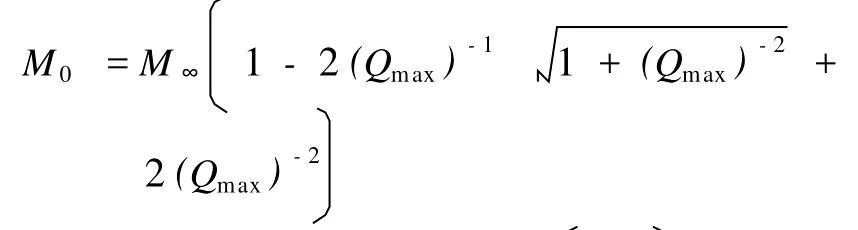
考慮到Q的取值范圍,忽略Qmax-1的平方項,則有:

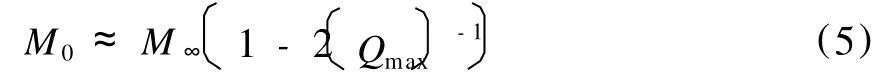
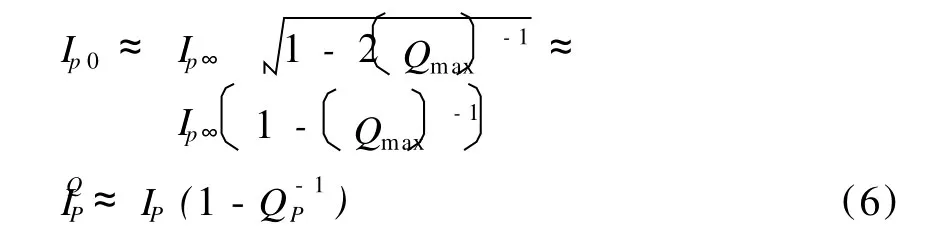
從式(6)看出,地層吸收作用的確對巖石彈性參數產生了影響,這種影響可能在大多數情況下是很小的,但是如果介質含烴,使介質吸收嚴重,那這種影響將比較大。

2 地層吸收對AVO的影響

當不考慮地下介質吸收的情況下,隨入射角θ變化的P波反射系數RPP,可以用Aki-Richard方程計算[9]:

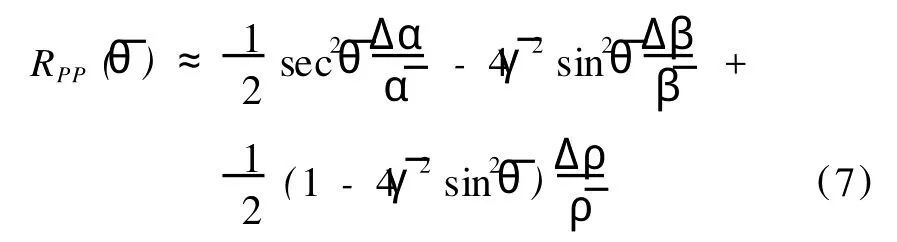
其中 R(ˉθ)表示隨角度變化的PP波反射系數;ˉα、ˉβ、ˉρ、ˉγ和ˉθ分別表示平均P波速度、平均S波速度、平均密度、ˉβ/ˉα比值,以及分界面的入射角和透射角的平均角度。類似的,Δ α、Δ β、Δ ρ是界面二側P波速度、S波速度,以及密度的變化量。

由于在小角度情況下,sin2θ≈tan2θ,并取S波和P波的背景速度比值=0.5,則由方程(7)就可以得到式(8)表示的W iggins方程[10]:

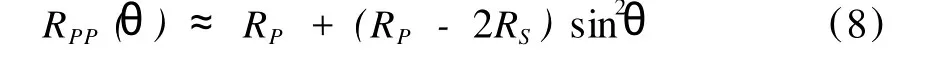
其中 RP和RS分別表示法向入射時縱波和橫波的反射系數。

利用式(6)對式(8)進行改寫得到:

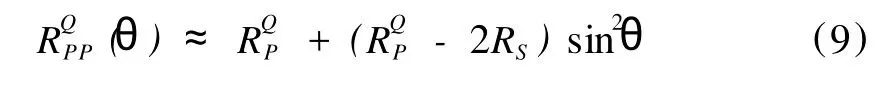
把式(8)、式(9)二式相減,得:

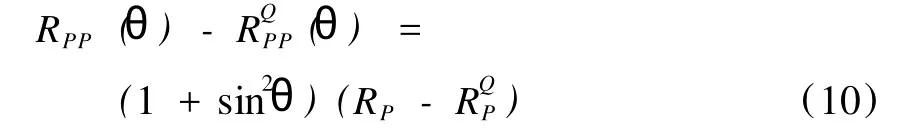
由于 RP=(IP2-IP1)/(IP2+IP1);

于是有:

由式(11)可知,在碎屑巖油氣藏中,如果砂巖中含有了油氣,那么其Q值比較小(一般小于50),而泥巖的Q值比較大(一般大于100)。所以式(11)中/2的值一般為正,也即AVO的截距和梯度由于吸收的影響,都以相同的衰減量減小。

下面通過四類典型的砂泥巖AVO模型來進行分析,模型數據見表1。

如圖2所示,圖2中深色點線表示不考慮吸收時的AVO曲線。從圖2(a)、圖2(c)看出,雖然泥巖的Q值從100變化到150,但是它們對應的AVO曲線幾乎重合;而從圖2(b)、圖2(d)卻明顯看出,下層砂巖的Q值從50變化到5,AVO曲線的形狀發生了顯著變化,截距與梯度都隨著Q值的減小而減小,當Q值取到5時,第一類AVO甚至轉化成了第二類AVO,而第二類AVO轉化成了第三類AVO,這說明了砂巖的吸收對AVO的影響比較明顯。

從圖3(見下頁)可以看出,地層吸收對第三類和第四類AVO的影響,與前二類基本相同。曲線的截距和梯度都隨著Q值的減小而減小,且下層砂巖的吸收,對AVO影響比上層泥巖要大。當砂巖吸收嚴重時,AVO的類型甚至發生了變化。

通過上面對四類AVO的分析可以得出,上層泥巖的吸收對AVO的影響非常小,而下層砂巖的吸收對其影響比較大。如果砂巖含氣,Q值很低時,AVO的類型甚至會發生變化:第一類AVO會轉化為第二類,第二類和第四類AVO會轉化為第三類,而第三類AVO保持不變。因此,當地震波在地下傳播過程中遇到儲層時,地層的吸收使地震波能量衰減,使其AVO響應的截距和梯度都減小。如果忽略這種影響,有可能使我們在利用AVO識別儲層時,誤把油層認為是氣層,把水層誤認為油層,從而造成錯誤的判斷。

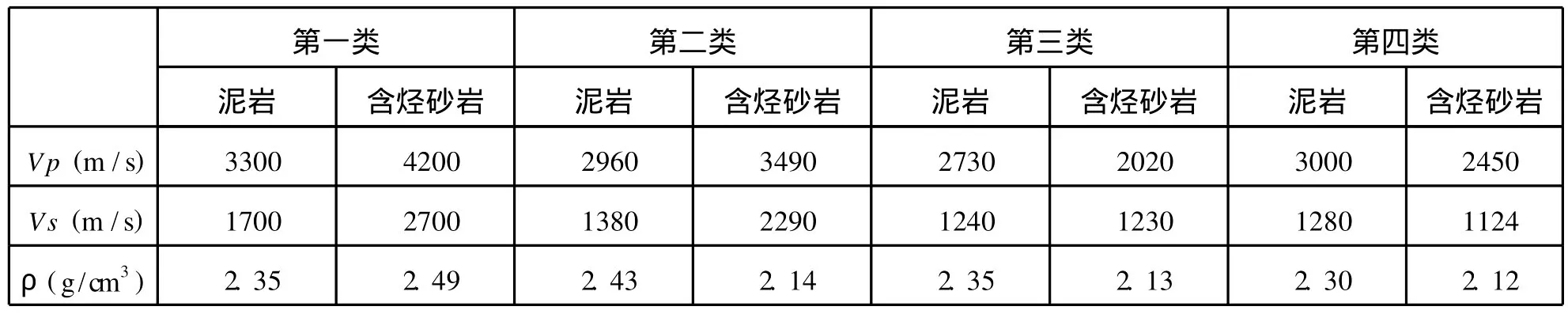
表1 四類AVO典型界面模型Tab.1 Stratigraphic models for four classes ofAVO

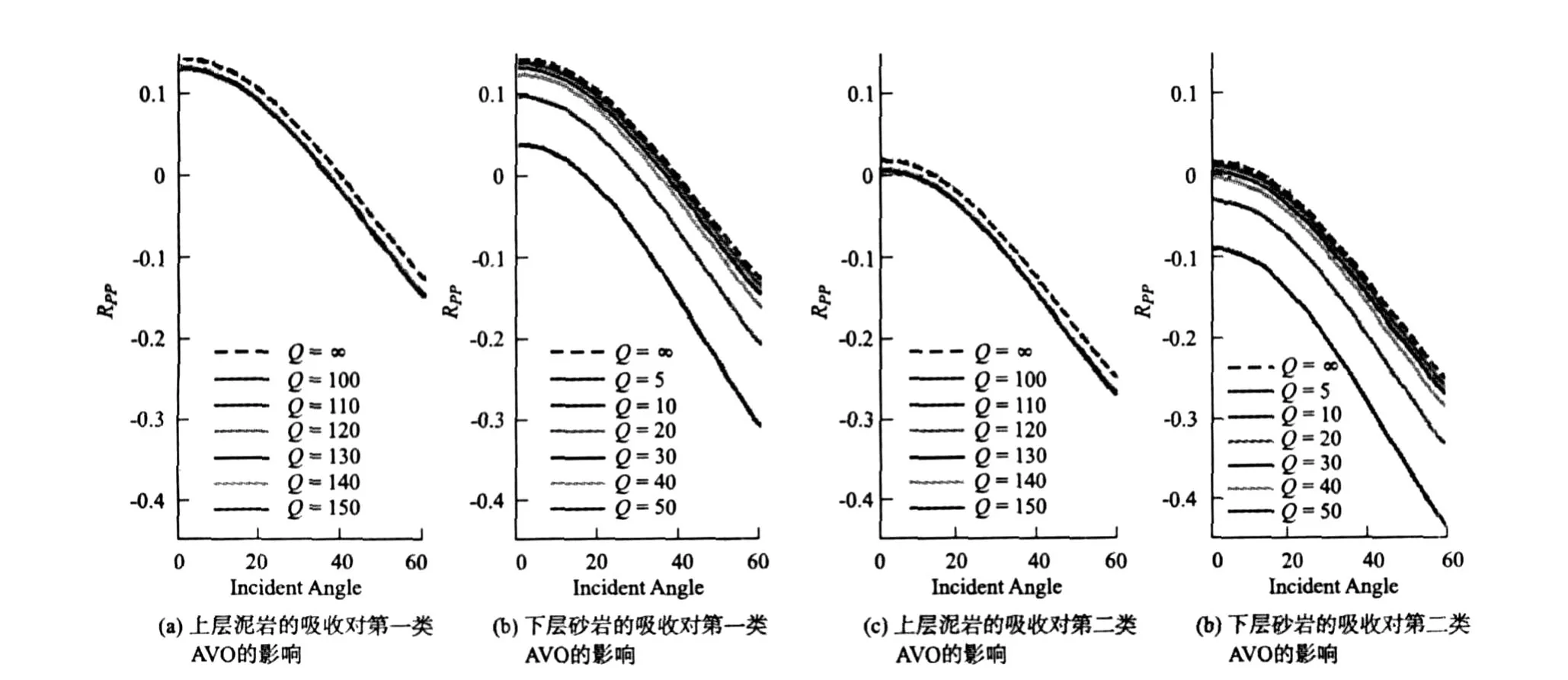
圖2 地層吸收對第一類AVO和第二類AVO的影響Fig.2 The effect of absorption on class 1 and class 2 ofAVO

圖3 地層吸收對第三類AVO和第四類AVO的影響Fig.3 The effect of absorption on class 3 and class 4 of AVO

3 地層吸收對彈性阻抗的影響

彈性阻抗是聲阻抗的推廣,它隨入射角的變化而變化,聲阻抗是入射角為零時彈性阻抗的一個特例[11]。常規彈性阻抗方程是基于Aki-Richard方程推導出來的,作者在本文將基于地層吸收情況下的W iggins方程來推導彈性阻抗方程。由式(9)得:

對其積分,最后可以得到彈性阻抗方程式(12)。

表2 用于驗證彈性阻抗方程的模型數據Tab.2 Model data to test the EI equation

與常規的彈性阻抗公式類似,EIQ表達式也存在著彈性阻抗值隨角度變化在量綱上有很大變化的問題,這不利于不同角度彈性阻抗值的對比。為了消除入射角變化對量綱的影響,可引入常量IP0和IS0對式(12)進行規范化,得到式(13):

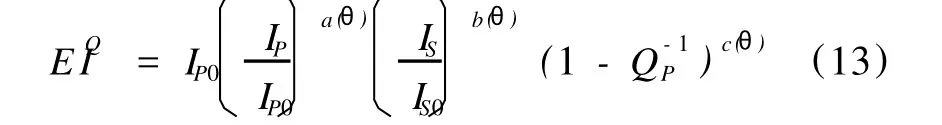
從式(13)容易看出,地層吸收對彈性阻抗也有影響,且這種影響隨著角度的不同而不同。下面,以Marmousi2模型為例來討論地層吸收對彈性阻抗的影響。在圖5所示的Mar mousi2模型中,第2 200道經過二套儲層(圖5中橢圓標注區)。從圖6中看出,不同角度的彈性阻抗值,都因地層吸收而減小,尤其是在儲層處更明顯,且隨著角度的增加,彈性阻抗值的衰減量也增加。充分利用這些性質,將有利于彈性阻抗在識別儲層方面的應用。

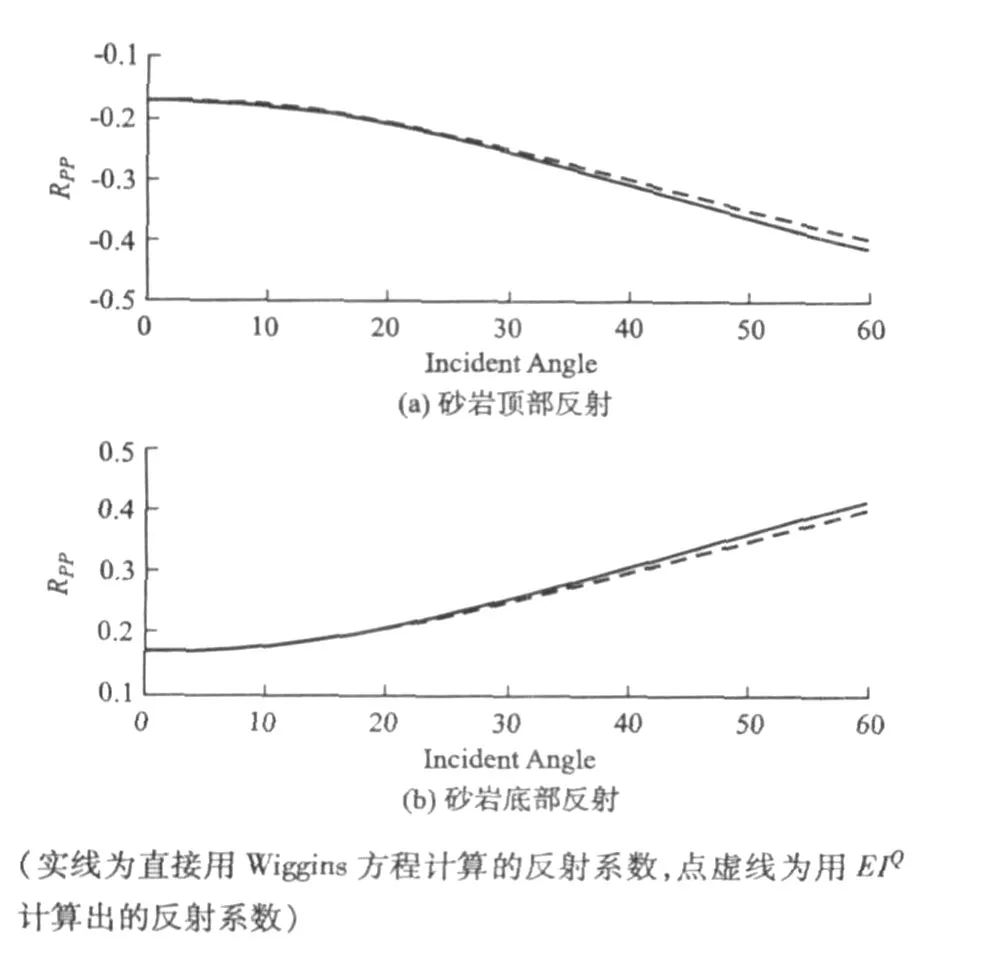
圖4 反射系數對比圖Fig.4 Comparison of reflectivities

4 地層品質因子與縱橫波阻抗QAVO反演

圖5 Marmousi2模型Fig.5 Marmousi2 model

彈性阻抗反演技術充分利用了疊前數據豐富的振幅和旅行時信息,利用了不同入射角的部份疊加數據體得到彈性阻抗數據體。利用彈性阻抗參數,可以分析地層在近、中、遠偏移距上的變化規律,也可以從其中提取出地層的縱橫波速度、密度、泊松比等巖性參數。用式(13)進行彈性阻抗反演與常規彈性阻抗反演類似,需要地震資料處理,測井資料標定,角度子波提取和彈性阻抗反演這幾個流程[12]。作者在本文中利用不同角度的疊前彈性阻抗結果,從EIQ數據體中同時提取出地層品質因子Q和縱橫波阻抗,來更好地指導儲層的預測。

對式(13)二邊取對數,可得:

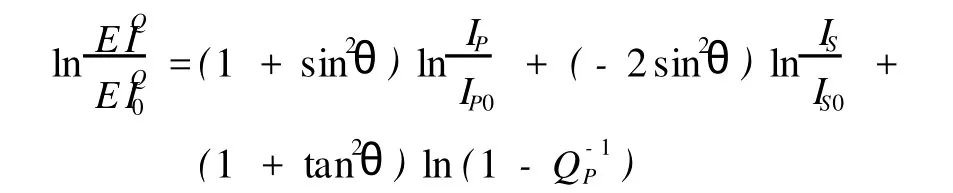
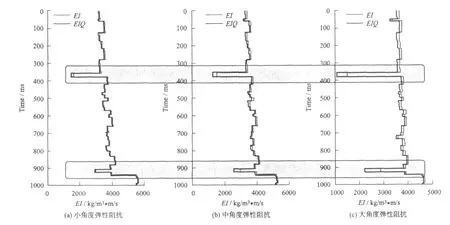
圖6 有吸收和無吸收情況下彈性阻抗曲線的對比Fig.6 Comparison of EI logs under the situation of absorption and non-absorption

為了得到縱橫波阻抗和品質因子,需要三個不同角度的EIQ數據體。將三個角度分別代入上式,并用矩陣形式表示為式(14)。

方程(14)的求解形如對AX=B的求解,由于角度已知,只需知道三個相互獨立的EIQ數據體,用最小平方法便可以求得縱橫波阻抗和品質因子。

但在實際應用中,直接利用方程(14)求解所得到的ln(IP/IP0)、ln(IS/IS0)和ln(1-Q-1P)值極不穩定,并且有些值不符合實際的物理和地質意義。因此,在實際應用時,是利用井資料先擬合方程中的系數。

可以證明,方程(14)可以寫成下面的形式:

其中 a′1、b′1、c′1;a′2、b′2、c′2;a′3、b′3、c′3為待定系數。

以ln(IP/IP0)為例,對于同一道的不同采樣點(即不同時間t)有:

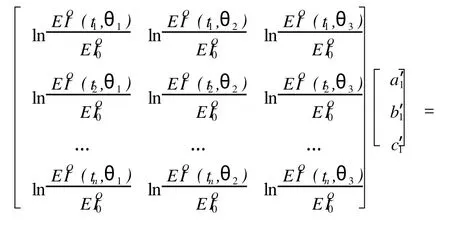
由于在計算系數a′1、b′1、c′1時,所用的EIQ數據體都來自于反演所得結果,因此,這些系數可選取反演得到的井旁道EIQ數據和測井曲線,通過最小二乘擬合得到。這種巖性參數與EIQ之間的關系最密切,得到的a′1、b′1、c′1也最具有代表性。

同理,ln(IS/IS0)和ln(1-Q-1P)對應的系數,也可以由該方法獲得,最后得到九個常系數a′1、b′1、c′1;a′2、b′2、c′2;a′3、b′3、c′3之后,將它們代入式(15),就可得到方程(20):

將反演所得的各角度EIQ數據體帶入方程(20),即可獲得各道任意采樣點處的縱橫波阻抗和地層品質因子。

5 實例分析

5.1 模型數據檢驗

以Marmousi2模型為例,對上述方法進行測試。首先利用圖7(見下頁)所示的Marmousi2模型參數,由式(13)求得三個角度的EIQ數據(角度值分別為25°、15°和5°),然后利用方程(20)從中反演出縱橫波阻抗和品質因子;圖8(見下頁)為EIQ數據中沒有噪音的反演結果,可以看出,在無噪音時,該方法可以完全恢復出Mar mousi2模型的縱橫波阻抗和品質因子值;圖9(見下頁)為加入5%噪音時反演的結果,反演結果與真實模型數據吻合很好;圖10(見下頁)為加入10%噪音時的反演結果,反演出的縱橫波阻抗和真實模型吻合很好,品質因子稍有抖動,但也有很好的相似性;圖11(見下頁)為從模型中抽出一道的顯示結果。經過測試表明,該方法是一種有效的求取縱橫波阻抗和品質因子的方法。

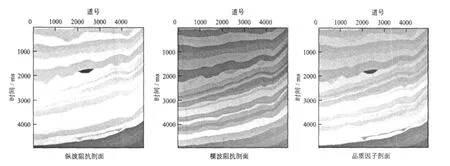
圖7 Mar mousi2模型參數Fig.7 Marmousi2 model parameters

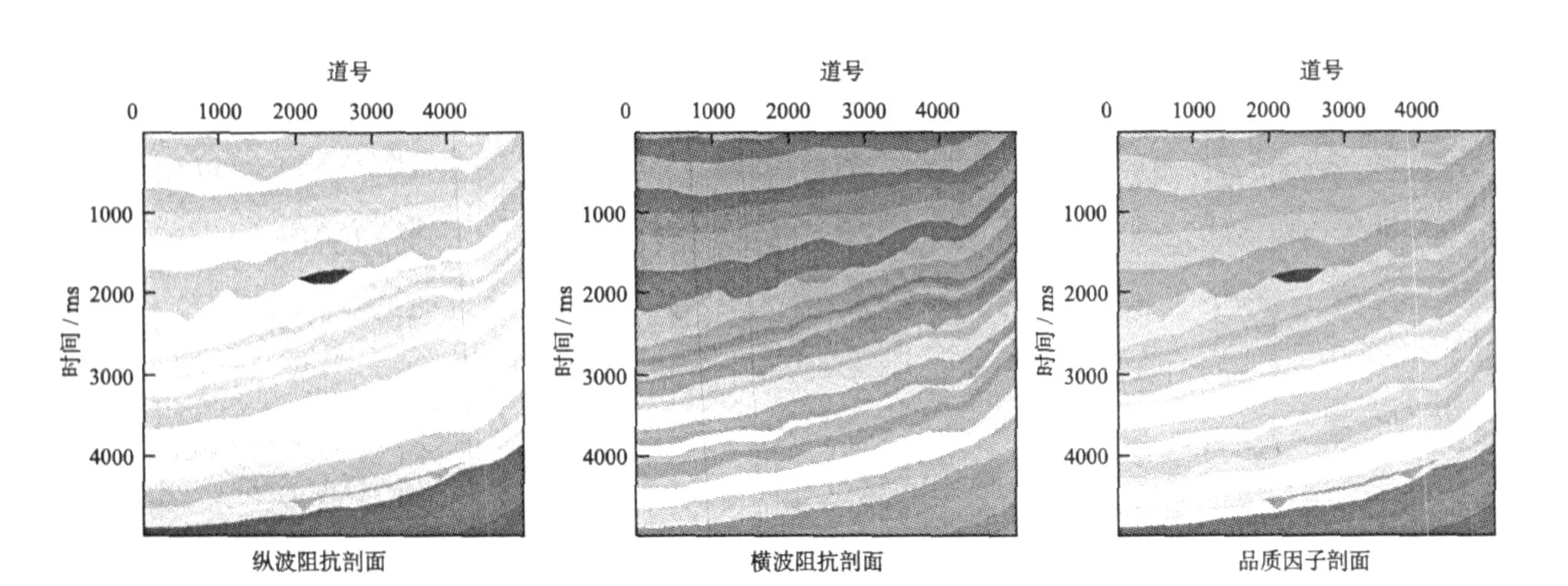
圖8 無噪時的反演剖面Fig.8 Inversion section with noise free seismology

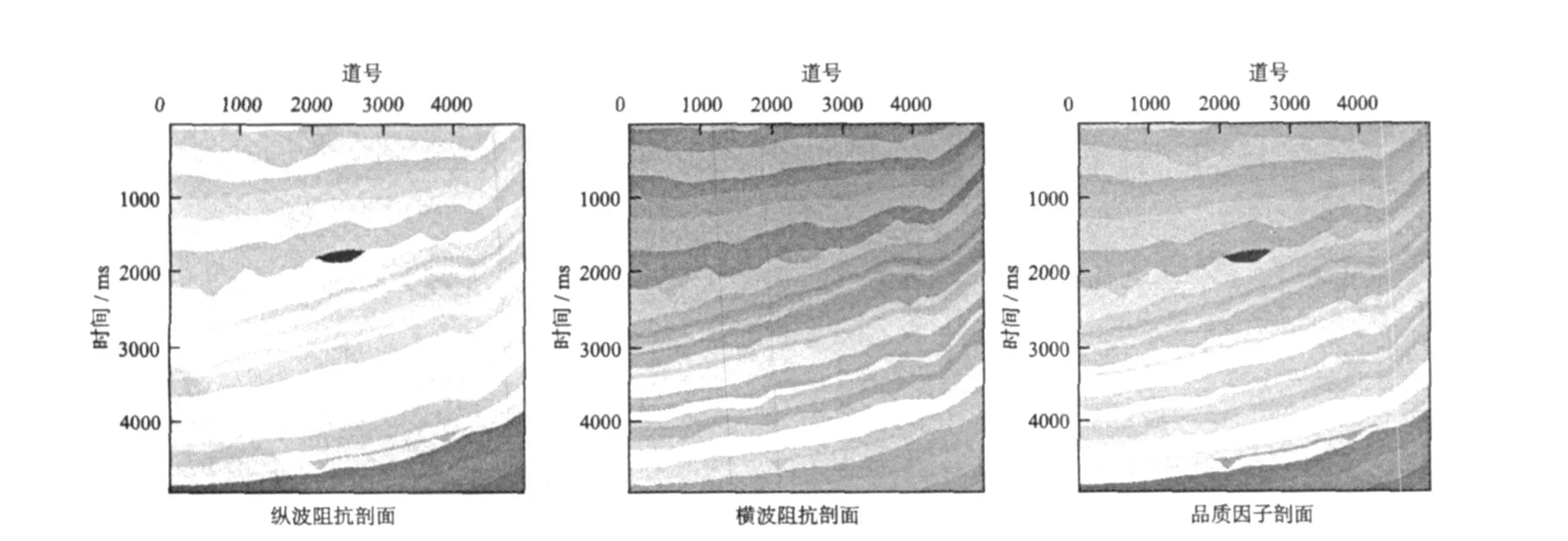
圖9 5%噪音時的反演剖面Fig.9 Inversion section with seismology containing 5%noise

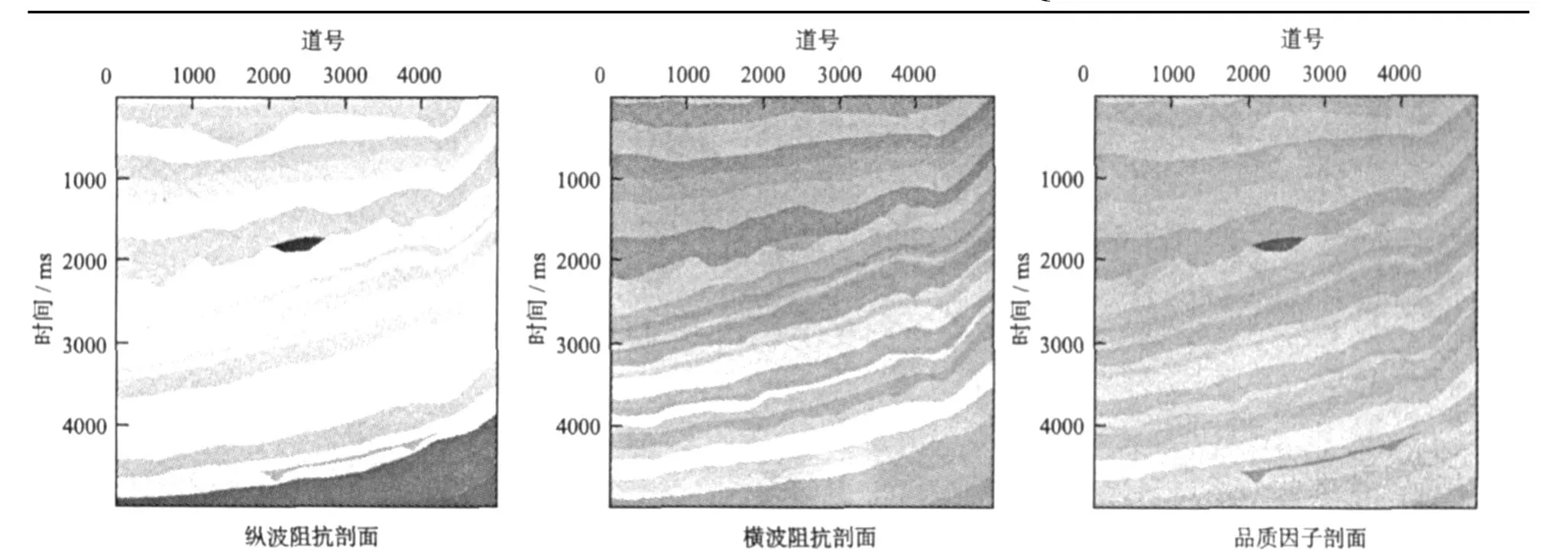
圖10 10%噪音時的反演剖面Fig.10 Inversion section with seismology containing 10%noise

圖11 反演結果曲線對比Fig.11 Comparison of inverted logs and model data

5.2 實際數據應用

在研究區的中層氣藏具備良好的巖石物理條件,測井資料顯示,氣層縱波速度較低,地震反射特征表現為強振幅、低頻率,具有亮點型反射特征。目的層處的砂巖儲層含氣后縱波阻抗明顯降低,由于孔隙流體類型對橫波的影響很小,所以目的層段的橫波阻抗與圍巖相當。

利用QAVO方法,從本區的疊前部份角度疊加地震數據反演得到相應的數據體,并從中提取出縱橫波阻抗和品質因子。圖12(見下頁)是在1.35 s處,穿過含氣儲層位置的縱橫波阻抗和品質因子時間切片,可以看出,縱波阻抗在含氣目標區表現為低值,切片上可明顯看出含氣砂體的大致范圍,而橫波阻抗切片上則看不出儲層范圍。品質因子在含氣目標區也表現為明顯低值,從而可以比較準確地推斷含氣砂體的空間展布。該結果與驗證井Y74的結論一致,表明了含氣儲層預測結果與實際情況吻合。由此可見,利用基于粘彈性理論的地層品質因子,與縱橫波阻抗進行QAVO同步反演是可行的。綜合利用品質因子和縱橫波信息,可以有效識別儲層,符合儲層含氣后縱波阻抗降低,橫波阻抗基本不變且吸收嚴重的規律。

6 結論

(1)從粘彈性介質的本構方程出發,作者在文中討論了地層吸收對波阻抗等巖石彈性參數的影響,給出了吸收前、后波阻抗之間的定量關系,證明了地層的吸收作用使波阻抗減小,特別是在含氣儲層段。

(2)作者在文中討論了地層吸收對地震AVO響應的影響,得出由于吸收使得P波反射系數的截距和梯度都發生減小的結論。并且通過四類AVO模型驗證發現,當吸收嚴重時,AVO類型甚至發生變化,會造成AVO假象。并進一步從考慮吸收情況下的W iggins方程出發,推導出了帶品質因子的彈性阻抗方程。

(3)利用疊前彈性阻抗反演框架,實現了地層品質因子與縱橫波阻抗的同步QAVO反演,并將地層的吸收特征與縱橫波阻抗等彈性參數相結合,進行綜合儲層表征,提高了儲層預測和烴類檢測的可靠性。

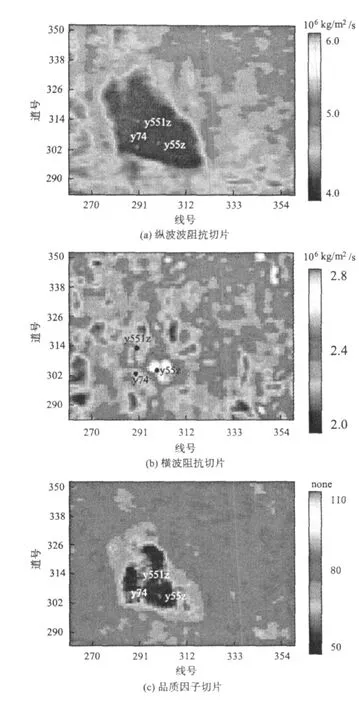
圖12 1.35 s處的各參數切片Fig.12 Inverted parameter slices at 1.35 s

[1] FUTTERMAN W I.Dispersive body waves[J].Journal of Geophysical Research,1962,67(12):5279.

[2] 張璐,白曉寅.單程波法地震波衰減特征數值模擬分析[J].物探化探計算技術,2009,31(6):541.

[3] UPENDRA K T,MCMECHAN G A.Effects of incomplete parameterization on full-wavefield viscoelastic seismic data for petrophysical reservoir properties[J].Geophysics,2007,72(3):O9.

[4] TONN R.The determination of the seismic quality factor Q from VSP data:A comparison of different computationalmethods[J].Geophysical Prospecting,1991,39(1):1.

[5] 尹陳,賀振華,黃德濟.基于二維粘滯性波動方程的地震波衰減理論研究[J].物探化探計算技術,2008,30(5):353.

[6] KOESOEMAD INATA A P,MCMECHAN GA.Petroseismic inversion for sandstone properties[J].Geophysics,2003,68(5):1611.

[7] JOSEM C.Wave fields in real media:Wave Propagation In Anisotropic,Anelastic And Porous Media[M].Seismic Exploration,2001.

[8] MAVKO G,MUKERJI T,DVORKIN J.Rock physics handbook[M].Cambridge University Press,1998.

[9] AKI K,R ICHARDS P G.Quantitative Seismology:Theory and Methods[J].W.H.Freeman and Co,1980:123.

[10]WIGG INS R,KENNY G S,MCCLURE C.A method for determining and displaying the shear-velocity reflectivities of a geologic formation[M].European patent Application,1983.

[11]CONNOLLY P.Elastic impedance[J].The Leading Edge,1999,18(4):438.

[12]王保麗,印興耀,張繁昌.彈性阻抗反演及應用研究[J].地球物理學進展,2005,20(1):89.