正確理解熱力學第三定律

蘇許輝

(寧波中學 浙江 寧波 315100)

高中人教版《物理·3-3》主要包括熱學的相關內容.熱力學的三大定律是熱學的基礎，課本對熱力學第一定律和第二定律已經有了比較詳細的介紹，而對第三定律只有簡單的一個表述：任何系統都不能通過有限的步驟使自身溫度降低到絕對零度，即絕對零度不可達到.

在教學的過程中，每次講到這里，都有不少同學對此充滿好奇，問：為什么絕對零度不能達到呢？由于受到高中物理知識廣度和深度方面的限制，許多老師和學生習慣于從分子動理論出發，對熱力學第三定律——絕對零度不能達到的原因進行了較片面地理解，不少老師也都是按下面的方法進行解釋的.

1 依據分子動理論對“絕對零度不能達到”進行解釋

根據經典熱力學，溫度是物體分子熱運動平均動能的標志，它們之間的關系可以表達為

(1)

式中，k為玻爾茲曼常量；i為分子各種運動自由度數，包括分子的平動自由度、轉動自由度、振動自由度.

從(1)式可見，由于物體內分子無規則運動的平均能量與溫度成正比，因此如果絕對零度能夠達到，則分子的平均動能為零，分子將處于完全靜止的狀態，而這與分子動理論對分子的熱運動的描述：“物體是由大量分子組成的，分子永不停息地做無規則運動”相矛盾.

上面依據分子動理論的知識，從經典熱力學做出的解釋好像能夠說明絕對零度為什么不能達到.但是隨著實踐的進展，經典熱學理論已顯示出它的局限性：如果在絕對零度下粒子是靜止不動的，那么它的速度為零，這時它的位置就是確定的.這樣的話，位置和速度兩者的值我們都知道了，這不符合海森伯的不確定原理——它只允許知道一個.所以，近代物理的量子理論對經典熱力學作了修正，指出：即使溫度能夠達到絕對零度，分子也不會完全靜止，因為分子還具有“零點能”.并且，零點能的存在已經從實驗中得到了證實.

可以看出，依據分子動理論的相關內容，從經典熱力學出發，認為分子在絕對零度會靜止不動的觀點是站不住腳的，以此來解釋絕對零度不能達到就有一定的局限性.

2 熱力學零度不能達到的原因

現從能斯特定理出發，來證明絕對零度為什么不可達到[1].

首先考慮降溫的手段，即考查經歷何種過程降溫最有效.顯然，放熱降溫當然有效，但又必須有更低溫度的熱源，這是不實際的.因此，只有絕熱降溫是可取的方式.這又有兩種選擇：可逆或不可逆.我們來分析這兩種方式.假定以(T，y)為獨立參數，y可能是實驗可控的體積、壓強等.

對于可逆過程，隨著溫度的增加系統的熵亦增加.在S-T圖(圖1)上，假定物體系由y1線上的一點A經歷絕熱可逆過程(熵不變，沿水平線)到達y2線的B點.兩狀態的溫度分別記為TA和TB.

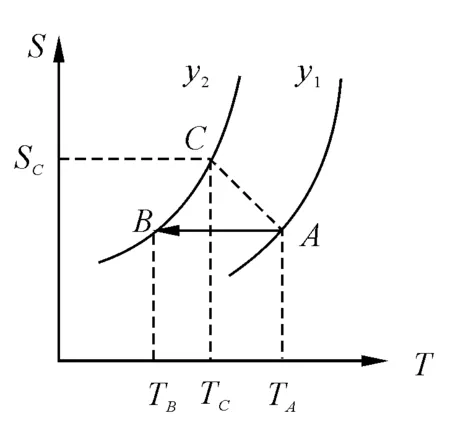
圖1 物體系熵隨溫度T和y的變化趨勢

如果由A經歷不可逆絕熱過程(熵增加)到達y2線，則應到達熵更大的一點C，顯然有

TC>TB

可見，可逆過程降溫更為有效，即絕熱可逆過程降溫是最有效的途徑，故而我們只討論絕熱可逆過程.

熵的計算公式

(2)

量子理論與實驗都給出，在極低溫度下，非金屬定容摩爾熱容CV∝T3，金屬CV∝T，所以

上述(2)式在T→0時收斂.并且，當物體系由A(TA，yA)經絕熱可逆過程(熵不變)至B(TB，yB)時，有

SA=SB

由能斯特定理

S(0,yA) =S(0,yB)

因而

(3)

如果

TA>0

則有

亦必有

TB>0

即絕熱可逆過程不能將溫度降至絕對零度.

因此，任何有限步驟都不能將體系的溫度降至絕對零度.

3 展望

熱力學第三定律雖明確指出，絕對零度不可能達到，但這并沒有阻止人們向這個最冷的極地逼近.早在1926年，德拜和吉奧克用磁冷卻法達到了10-3K.后來又有人攻破了10-6K.1995年，科羅拉多大學和美國國家標準研究所的兩位物理學家愛里克·科內爾和卡爾威曼成功地使一些銣原子達到了令人難以置信的溫度，即2×10-8K.2003年，科學家更獲得5×10-10K.當然，我們相信科學家一定還可以達到更低的溫度.然而，人們發現，溫度越低，進一步逼近絕對零度就更加困難.這所有的努力都說明熱力學第三定律的正確，即絕對零度是低溫的極限，是不可能達到的.

參考文獻

1 王竹溪. 熱力學. 北京:高等教育出版社,1955.355～365