斜交剛構橋設計的幾個關鍵問題
楊鳳蓮
(中鐵第四勘察設計院集團有限公司,武漢 430063)
剛構橋按墩軸線與梁體中心線交角可分為正交剛構橋及斜交剛構橋。斜交橋較正交橋有以下特性[1]:(1)簡支斜板的縱向主彎矩比跨徑為L、寬度為b的正交板彎矩要小,并且隨斜角的增大而遞減。(2)斜板的鈍角部位,在與鈍角等分線相垂直方向將產生接近跨中彎矩值相當大小的負彎矩,斜交橋跨中橫向彎矩與正交橋有很大的差異,一般較之為大,斜角變大,橫向彎矩增大,并且與抗扭剛度有關,抗扭剛度越大這種隨角度變化的反應越敏感。(3)斜交橋在荷載作用下,支座反力不均勻,銳角反力減小,鈍角反力增大。斜交剛構橋是剛構橋中的特例,斜交剛構橋設計要在正交剛構橋設計基礎上考慮更多因素。以某斜交剛構橋為例,通過對其梁部、剛臂墩、樁基礎設計中幾個關鍵步驟的分析,闡明斜交剛構橋設計中的幾個需要注意的關鍵問題。
1 工程概況
某鐵路剛構橋,梁體中心跨徑(13.5+16+13.5)m,0.8UIC荷載,雙線,墩軸線與梁體橫向交角41°,端部截面與線路中心線正交,墩頂處梁高1.7 m,跨中處梁高1.2 m,橋面寬12.2 m,截面形式如圖1~圖3所示。

圖1 跨中截面(單位:cm)

圖2 剛構中心剖面

圖3 剛構平面
2 梁部設計
2.1 建模方法
主梁采用鋼筋混凝土結構。由于墩梁斜交,梁體沿橫向內力分布不均勻,若采用空間實體單元建模,分析和計算均比較費時,用橋博程序平面桿系結構建模,由于邊跨跨度沿梁體橫向是變化的,可取剛臂墩邊線所在縱向截面建模,所建模型一邊跨大一邊跨小,計算出各單元截面的配筋量,再將全梁配筋沿中跨跨中對稱線按大配筋量取對稱。這樣,建模計算各單元截面所需配筋量比實際略偏大,相對于建立空間實體模型計算,是一種省時、安全、實用的計算方法。建模時還有一點要注意:模型不計基礎的溫度及收縮徐變效應,這是由于基礎埋在地下,受溫度變化等影響不明顯。
2.2 主筋計算[3]
從全橋縱向分析結果提取各單元內力,據鋼筋混凝土結構設計原理計算出梁部各單元截面配筋。縱向鋼筋為受力鋼筋,配筋長度應綜合考慮受力需要與錨固長度,鈍角處頂板橫向鋼筋要加強。
2.3 腹筋計算[2~3]
箍筋和斜筋用來抵抗剪應力,當各節點處的剪應力均小于無箍筋及斜筋時的主拉應力容許值[σtp-2]時,箍筋和斜筋不需計算,采用構造配筋;若有節點處的剪應力大于主拉應力容許值[σtp-2]時,混凝土多半要開裂,裂縫首先出現在主拉應力較大處,并沿斜向延伸,在延伸所及的梁段內,主拉應力全由箍筋和斜筋承擔,不考慮混凝土的抗剪作用。計算時首先選定某根斜筋所轄范圍L,可畫出該范圍內的剪應力圖,用剪應力圖面積可確定出該范圍所需的箍筋及斜筋。但在主拉應力小于[σtp-3]部分梁段內,主拉應力可由混凝土承受,僅按構造要求配置腹筋即可。
3 剛臂墩設計
剛臂墩為壓彎構件,根據設計經驗,一般最大彎矩(絕對值)為控制工況,最小軸力與最大軸力工況不控制設計,剛臂墩與梁固結處彎矩最大。墩身內力Px、My、Nz可從縱向分析結果中提取,X、Y、Z分別為沿線路方向、垂直線路方向及豎直方向,墩身內力Py、Mx由橫向搖擺力、風力及離心力(曲線)引起。由于墩軸線方向與所得內力方向斜交,直接用以上內力計算剛臂墩配筋有困難,可采用以下辦法解決:將內力分解為垂直墩軸線及平行墩軸線方向,分別組合,再將剛臂墩按照偏心受壓構件計算配筋。
4 樁基礎設計
4.1 樁基模擬
樁基計算用B90程序,求出單位力作用下的樁頂位移及轉角,將群樁模擬成獨樁,將邊界條件模擬成在樁頂加一土彈簧[5],樁底固結,再根據虛功原理[6],可求出所模擬獨樁的截面尺寸及土彈簧彈性系數,將這些參數代入橋博程序。對斜交剛構,須用自定義布樁方式。
4.2 樁頂力計算
4.2.1樁頂力Px、My、Nz的計算
樁頂力Px、My、Nz從全橋縱向分析結果中提取。由于橋梁博士模型里承臺底加了一土彈簧,對樁頂內力有一定影響,所以,從橋博程序里不宜提取樁頂內力,而應提取墩底內力Px、My、Nz,再通過換算轉換成樁頂內力。注意橋博程序里的內力Px、My符號與B90程序中是反號的,在輸入B90程序時要加“-”號;如果從橋博程序里提取的是承臺頂內力,則要注意輸入B90程序時內力符號換算關系有變化。
4.2.2樁頂力Mx、Py的計算
樁頂力Mx、Py由橫向搖擺力、風力、離心力及汽車橫向撞擊力組成[4]。橫向搖擺力、風力方向可以指向一側,也可以指向另一側,所以要分正負與Px、My、Nz分別組合成不同工況。橫向搖擺力按100 kN的集中力作用在軌頂,平移到樁頂為100 kN的水平力及彎矩。風力計算是按一個橋墩承擔其兩側各半跨梁上的風力,風力包括列車或聲屏障風力、梁上風力及剛臂墩風力。離心力指向曲線外側,離心力的計算是將離心力系數乘以靜活載引起的墩頂軸向力。如剛臂墩是在公路邊且沒有防護措施,則需計汽車撞擊力的作用。縱向撞擊力可直接在橋博平面桿系程序中施加,橫向撞擊力要在空間模型里加載,這是因為剛臂墩與梁固結,一個墩受到撞擊,其他墩會分擔一部分撞擊力,只有用空間模型才能實現“撞擊力的分配”。如1號墩上作用1 000 kN的橫向撞擊力,撞擊力作用點距樁頂3.5 m,將該力平移到樁頂,會產生1 000 kN水平剪力及3 500 kN·m橫向彎矩,但空間模型計算結果為:1號墩樁頂只產生800 kN的水平剪力及2 300 kN·m的橫向彎矩。
4.2.3 樁頂“斜交彎矩”的計算
由于斜交剛構橋荷載沿墩橫向分布不均勻,由此可以推斷,在樁頂會產生一繞梁中心軸線的橫向彎矩及垂直梁軸線的縱向彎矩,由于墩梁斜交引起,簡稱“斜交彎矩”。建立空間有限元模型,來計算荷載沿墩橫向的分布(圖4),只建立梁部模型,在墩梁相接處取幾個節點加固定約束,在邊支座中心處加橫向及豎向約束,荷載按橋面實際位置,分不同工況施加,那么,加約束處的支反力即代表沿墩橫向荷載的分布。表1示出一種活載工況下,1號墩沿墩橫向的荷載分布及“斜交彎矩”結果。表中NODE指沿墩橫向所加固定約束的節點號,FZ指1號墩上加約束處的支反力,X、Y為1號墩約束處至墩中心(節點292)的距離,MY、MX為各約束點的“斜交彎矩”,ΣMY、ΣMX為1號墩樁頂的“斜交彎矩”。 從表1可看出:該工況下荷載沿墩橫向分布很不均勻,中跨鈍角處199號節點荷載分布最大,銳角處248號節點荷載分布最小,甚至是向上的荷載。
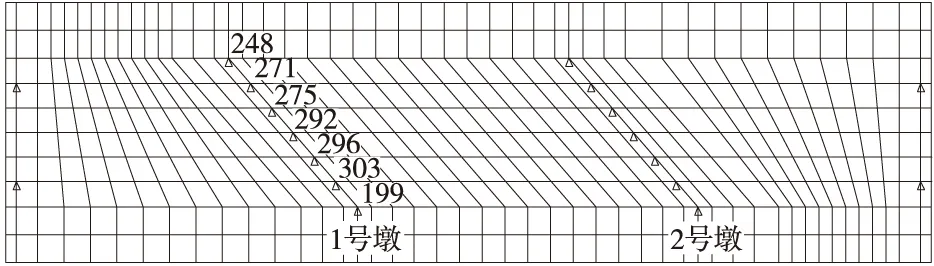
圖4 空間有限元模型平面

表1 1號墩沿墩橫向荷載分布及“斜交彎矩”(雙線,向左行車,重軸在中跨跨中)
各工況下1號墩的“斜交彎矩”如表2所示,表2中所列“重軸在1號墩”及“重軸在中跨跨中”均指沿梁體中心線的位置。

表2 1號墩各工況下的“斜交彎矩” kN·m
從表2可看出,在自重及二期恒載作用下,“斜交彎矩”較小,這是因為本剛構是梁端正交的多跨剛構連續梁橋,而自重及二期恒載沿全梁接近均布,所以沿墩橫向荷載分布較均勻。如果是單跨或梁端斜交剛構,則荷載分布沿墩橫向從鈍角向銳角逐漸減小。總“斜交彎矩”大小應由自重+二期恒載+基礎相對變位+活載引起的“斜交彎矩”組成。從表2中可看出,工況6、9、11、12不控制設計,其余幾種活載工況與恒載工況、基礎相對變位工況引起的“斜交彎矩”分別與4.2.1、4.2.2中樁頂力組合作為輸入B90計算程序的荷載。事實證明,“斜交彎矩”對樁基配筋及樁長均有一定影響,墩軸線與梁體橫向交角越大,“斜交彎矩”越大,設計時不可忽視。
[1]車宇琳,馮云成,包琦瑋,等.橋梁設計常用數據手冊[M].北京:人民交通出版社,2005.
[2]TB 10002.3—2005,鐵路橋涵鋼筋混凝土和預應力混凝土結構設計規范[S].
[3]黃 棠,王效通,等.結構設計原理[M].北京:中國鐵道出版社,1988.
[4]TB 10002.1—2005,鐵路橋涵設計基本規范[S].
[5]TB 10002.5—2005,鐵路橋涵地基和基礎設計規范[S].
[6]邵旭東,程翔云,李立峰,等.橋梁設計與計算[M].北京:人民交通出版社,2006.

