鋼筋混凝土球形水塔設計分析和研究

尹華容

(中鐵工程設計咨詢集團有限公司,北京 100055)

1 概述

鋼筋混凝土球形水塔為新型水塔,其水箱為球形殼體結構(雙向曲面殼體),支承結構為支筒式(或支架式)。該種結構經久耐用、造型新穎美觀,主要由水箱、塔身、基礎和一些附屬設施組成。結構上的豎向作用有自重、水重、設備重、活荷載、豎向地震作用,水平作用有風荷載和水平地震荷載。水塔是一種高柔構筑物,它的荷載主要集中在結構頂部,在水平地震作用下作水平擺動,同時也隨著地面的豎向震動發生豎向運動。

鋼筋混凝土球形水塔的主體結構由3部分組成：水箱、支承結構(支筒或支架)、基礎,結構受力分析可按這三部分分別進行分析計算,然后進行地基承載力和結構整體穩定計算。

2 水箱結構設計

2.1 水箱內力分析

球形水箱的設計應滿足結構安全及經濟、合理性要求。從計算上看,球形水箱支承在球體的赤道上(圖1)內力小、穩定性好,可用簡化的薄膜內力分析,誤差很小,故一般的球形容器多支承在球體的赤道上,特別是鋼球容器更為多見,如化工、石油系統的貯氣罐、貯液罐等即是如此。但若將球形水箱支承在球體赤道上,則顯示出結構比較粗笨,且造價較高。而采用較細的支筒支承水箱(圖2),造型美觀,但這種支承方式造成了水箱支承處球殼內力分析的復雜性,采用簡單的薄膜內力法計算水箱誤差較大。

圖1 球體赤道支承

圖2 球體底部支承

球形水箱的受力狀態,雖然風荷載是其靜力計算的主要水平荷載,但對水箱的受力狀態影響有限,可不考慮。水箱的設計荷載主要考慮水箱內水壓力、結構自重和球頂雪荷載或活載,對于水箱頂部積灰荷載,實際上不起控制作用,可忽略，球體受力示意見圖3。

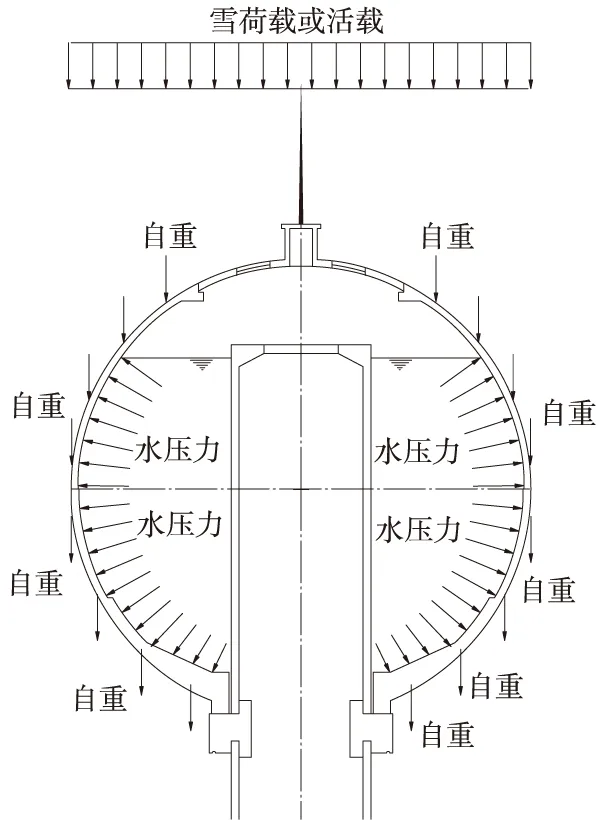
圖3 球體受力示意

對于球形水箱的內力分析方法,有兩種方法：(1)無彎矩理論也稱薄膜理論，計算只考慮殼體結構內的軸向力(徑向力和環向力),不考慮殼體內及邊緣處的彎矩,在殼體節點處按構造要求對殼體邊緣處適當加固,以考慮邊緣處變矩作用。這種計算方法適合于容積不太大的水箱；(2)有彎矩理論，計算除考慮殼體的軸向薄膜內力外,尚應考慮殼體邊端彎矩作用。如何考慮邊端彎矩的作用,目前也有兩種,一種是按邊端為固支計算球殼邊端處的彎矩對這該部件的影響,而不考慮在連接處相互作用的影響；另一種則是要考慮邊端節點處的彎矩分配或邊界處各種干擾力的作用下,對殼體內力干擾的作用影響。有彎矩理論計算方法中的后者比較合理,特別是考慮邊界干擾力的作用下對殼體內力干擾的作用影響的計算方法,相對更為實用和符合實際試驗所測試的結果。這種計算方法適合于大容積水箱或應用計算機進行計算。

考慮到目前球形水箱的容量不是很大,為計算快捷,經多次研究及試驗,仍采用薄膜內力分析法計算球形水箱,但由于支承邊緣處球體內力復雜,根據設計經驗可采取構造加強措施進行加固,以保證結構安全。當然也可按邊緣干擾理論進行內力分析,但計算繁瑣。

2.2 水箱內力計算

(1)球形水箱是一個沿自身的某一水平圓線A-A支承的整球殼(圖4)。水箱的主荷載是水的壓力,它垂直于殼體并與高度成比例，假設水箱裝滿水到球殼頂點，則球形水箱計算公式推導如下。

圖4 球形水箱計算簡圖

①水的法向壓力

Pr=γa(1-cosφ)

(1)

根據文獻[2]，球殼結構內力應滿足公式(2)

(2)

球形水箱a1=a2=a,代入公式(2)得

Nφ+Nθ=Pra

(3)

式中Nφ——球形水箱徑向力；

Nθ——球形水箱環向力；

a——球形水箱半徑；

Pr——球形水箱中的水壓力；

φ——球形水箱頂點至水箱任意點處的半徑夾角；

γ——為水(液體)的容重。

軸對稱荷載的徑向力

(4)

進行積分則

(5)

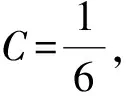
(6)

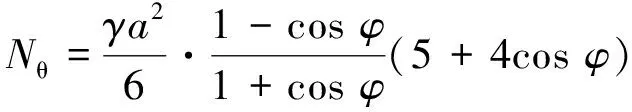
(7)

(8)

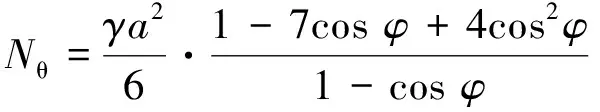
(9)

根據球形水箱的情況,當水箱支承部分(A-A)以下部分不需要,只有A-A以上部分時,可只采用φ<φ0部分的公式計算,即公式(6)、(7)；當有A-A以下部分時,A-A以下部分采用φ>φ0部分的公式計算,即公式(8)、(9)。

(2)按實際水壓力(設計最高水位)及自重共同產生的內力,則球形水箱計算公式推導如下(圖5)。

圖5 計算簡圖

①水壓產生的內力

作用在球面法向力為

Pr=γ(h-a·cosφ)

(10)

式中h為設計最高水位離球心的深度。

經推導求得徑向力為

(11)

式中φ0為設計最高水位處的中心角。

環向力為

cosφ0(cosφ0+cosφ)]

(12)

②球殼自重產生的內力

作用在球體面法向力為

Pr=γct.cosφ

(13)

式中γc——混凝土的比重；

t——球殼厚度。

經推導求得徑向力為

(14)

式中P為球殼任意截面以上的總重力。

環向力為

Nθ=Pr·a-Nφ

(15)

將式(14)代入式(15),得

Nθ=γcta·cosφ-Nφ

(16)

(3)兩種計算方法比較：在球形水箱計算中,用兩種方法分別計算,然后進行結果比較,經過多次對比,兩種計算結果環向力Nθ誤差不大,徑向力Nφ相差較大,但考慮到混凝土抗壓強度大,即使按簡單方法(第一種方法)計算,也不會影響結構安全。

(4)設計需要重點注意：球形水箱的計算半徑是采用徑向半徑,是定值,但結構受力上部小,下部大,因此球殼厚度和配筋沿整個球殼變化較大,下部球殼厚度和配筋則相應大些。箱體與下環梁交界處的內層徑向鋼筋適當加強,以抵御箱體邊緣的干擾力矩。

對一般水塔水箱的球殼頂和球殼底可不驗算球殼的穩定性。對在設計大型球形水箱時,由于水箱球形半徑較大,而支筒較細時,支承點在球殼底,存在失穩的可能,因此對大型水箱的球殼底的穩定臨界力應進行驗算。

3 支筒結構設計

支筒上的豎向荷載有水箱重、自重(含設備重和活荷載)、豎向地震作用；水平荷載有風荷載和水平地震作用；另外,對于支筒式水塔,由于支筒直徑小,高度大,支筒設計尚應考慮在風荷載、施工偏差、基礎傾斜等影響下,結構產生水平變位后,由豎向荷載引起的附加力矩。

3.1 地震作用

水塔的自振周期是水塔結構動力特性的標志,周期數值的大小一般與水塔的地震荷載值大小成反比。水塔支承結構可按底部固定于基礎上的懸臂結構計算,由于上部水箱為質量較大集中荷載,故在計算水塔結構自振周期時,可只考慮基本振型(第一振型),可不考慮多振型的影響。通過資料研究,第二、三振型對水平地震力和彎距的影響分別占5%及2%以下。

水平地震作用的計算方法,在《建筑抗震設計規范》(GB50011—2001)中,推薦了底部剪力法和振型分解反應譜法2種計算方法,但沒明確水塔抗震驗算時怎樣選用。另外探索是否可簡化為單質點體系進行簡化計算,現對這3種計算方法進行分析對比,并提出設計建議。

(1)底部剪力法

結構水平地震作用按下列公式確定(圖6)

圖6 地震作用簡圖

FEK=α1Geq

(17)

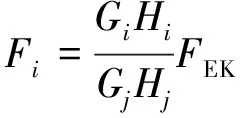
(18)

式中FEK——結構總水平地震作用標準值；

Geq——結構等效總重力荷載,單質點應取總重力荷載代表值,多質點可取總重力荷載代表值的85%；

Fi——質點i的水平地震作用標準值；

Gi,Gj——分別為集中于質點i、j的重力荷載代表值;

Hi,Hj—分別為質點的計算高；

β1——與場地土有關的系數。

(19)

按公式(19)計算結果見表1。

表1 水平地震作用下水塔總彎矩

(2)振型分解反應譜法

只考慮基本振型(第一振型),公式如下

F1i=α1γ1X1iGi

(20)

式中F1i——第一振型i質點的水平地震作用標準值；

α1——相應于第一振型自振周期的地震影響系數；

γ1——第一震型的參與系數；

X1i——第一震型i質點的水平相對位移。

將支筒分為9等分,水箱離支筒頂高度近似按0.1H考慮；每段支筒重

可推算出總力矩

(21)

計算結果見表2。

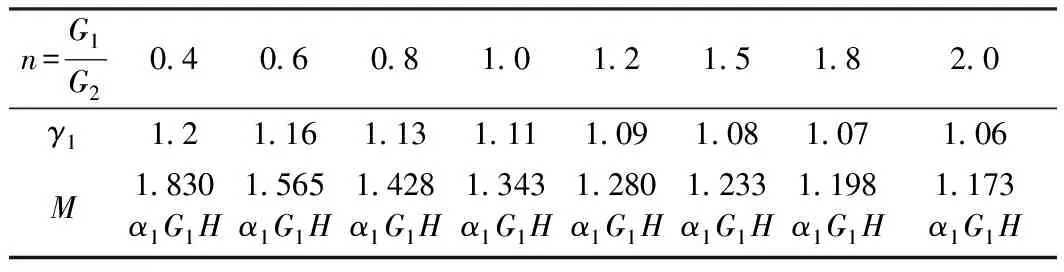
表2 水平地震作用下水塔總彎矩

(3)單質點體系法

按單質點考慮,計算公式如下。

(22)

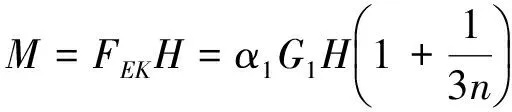
(23)

按公式(22)、(23)計算結果見表3。

表3 水平地震作用下水塔總彎矩

(4)結論

①計算結果對比：底部剪力法(表1)較振型分解反應譜法(表2)大1.15～1.36倍,較單質點體系法(表3)大1.16～1.36倍,底部剪力法最大,振型分解反應譜法與單質點體系法接近。

②底部剪力法適用于以剪切變形為主且重力分布都比較均勻的構筑物。這些條件顯然只能適用于高度較低且水箱直徑和支承直徑相接近的水塔。

③振型分解反應譜法是一種比較通用的計算方法.特別是對高度較大截面變化多或帶坡度的高大水塔較為適宜。

④單質點體系法計算較簡便,結果與按振型分解反應譜法計算接近,故對高度較大、支筒較輕、截面變化小的鋼筋混凝土球形水塔均較適宜。

3.2 風荷載

將支筒分為若干段,水箱為其中一段計算風荷載,并采用集中風力,作用點在各段的形心處。

3.3 附加力矩

附加力矩指考慮結構在施工偏差和荷載作用下產生變位后所引起的彎矩增量,即針對已知荷載作用下產生的彎矩而言。例如水箱和支筒上的風荷載和支筒上門窗孔洞所引起的重心偏移,引起結構變位產生的彎矩增量,對一般結構并非必需計算的內容。對于球形水塔這樣的高柔結構附加力矩可占風彎矩的30%以上,因此不能忽略附加彎矩的計算。

4 結語

(1)鋼筋混凝土球形水塔的結構受力分析可按水箱、支筒、基礎3部分分別進行結構分析計算,然后進行地基承載力和結構整體穩定計算。

(2)水箱結構的內力分析按無彎矩理論(也稱薄膜理論)和有彎矩理論均可,但通常采用簡便的無彎矩理論,但需在支承邊緣處采取構造措施加固或加強；計算方法按僅考慮滿水壓力作用的簡便計算能確保結構安全,若按實際水壓力及自重共同作用更精確。但需注意球殼厚度應自上而下逐漸加厚,對大型水箱的球殼底的穩定臨界力尚應進行驗算。

(3)支筒按懸臂結構進行計算,應考慮風荷載、地震作用、地基傾斜、施工及水箱安裝偏差造成的支筒附加力矩。支筒應分段計算風荷載,地震作用可按單質點體系法計算,并應考慮附加力矩的影響。

[1]S.P鐵摩辛柯,J.M.蓋萊.彈性穩定理論(第2版)[M].張福范，譯.北京.科學出版社，1965.

[2]W.氟留蓋.殼體中的應力[M].薛振東，等譯.北京：中國工業出版社，1965.

[3]王肇民.高聳結構設計手冊[M].北京. 中國建筑工業出版社，1995.

[4]M.L.賴姆佰特，等.筒倉理論與實踐[M].顧華孝，譯.北京：中國建筑工業出版社，1981.

[5]杜東升，等.高聳塔臺結構豎向地震模擬震動臺試驗研究[J].特種結構，2003(2).

[6]GB50011—2001，建筑抗震設計規范(2008年版)[S].