非線性系統的多項式近似表示及電力系統應用(Ⅰ)——理論篇
孫玉嬌, 劉鋒, 梅生偉
(清華大學電機系電力系統國家重點實驗室,北京 100084)
0 引言
電力系統是典型的包含有周期性函數的高維非線性系統,其平衡點的求解在電力系統暫態穩定分析中占有重要地位。雖然目前已有多種方法[1-9]可以有效求解出一些具有特殊形式的(如電力系統的經典模型等)系統的不穩定平衡點(UEP)或主導不穩定平衡點(CUEP),但一般性的平衡點求解問題在電力系統暫態穩定分析中還是一個開放性問題。根據暫態穩定域邊界理論[10],暫態穩定域邊界由穩定域邊界上UEP(一定條件下為1型UEP)的穩定流形的并集組成。通常,電力系統暫態穩定分析中主要關注穩定域邊界上UEP的求解。目前已有的UEP求解方法還難以獲知穩定域邊界上的UEP個數及分布情況。這對于獲取給定系統的穩定域邊界的整體結構及穩定域邊界求解造成了困難。
本文提出利用多項式近似系統研究電力系統平衡點求取及穩定域邊界近似的方法。這一方法的出發點源于多項式系統相對于一般非線性系統在平衡點求解上具有的優勢,它包括:1)基于代數幾何理論可對多項式系統的實根個數進行估計[11-12];2)采用適當的同倫方法可求得多項式系統的全部實根[13-16]。
采用本文所提方法首先要面臨的問題是對一個高維非線性系統如何計算它的多項式近似表達。半張量積方法為我國著名控制學家程代展教授提出[17],其本質是多線性映射的矩陣表達,它對多項式系統的表達與操作非常方便且易于計算機自動實現,因此,我們采用半張量積方法實現非線性系統多項式近似的自動求取。
其次采用本文所提方法需要面臨的問題是能否用多項式近似系統來研究原系統的平衡點并進行穩定性分析。對此,本文從理論上證明,當近似精度足夠時近似系統與原系統平衡點可以任意接近且其相對應的不穩定平衡點類型可以保持不變,這就為利用多項式近似系統研究原系統的平衡點及穩定域邊界近似奠定了理論基礎。
本文在所給的理論基礎上,將半張量積方法用于電力系統暫態穩定性分析,有可能實現電力系統暫態穩定性分析的“機械化”。這正是本文工作的最終目標所在,盡管目前的工作仍很初步,但它卻為電力系統暫態穩定分析方法提供了一個可能的方向。
1 半張量積方法簡介
半張量積方法[17]的本質是多線性映射的矩陣表達,它能夠實現維數不匹配矩陣的乘法運算,并且該矩陣乘法在一定條件下具有交換性,這兩個優點對于高維矩陣的運算是非常好的性質,它大大簡化了高維系統的近似表達式的計算復雜性,使得一般高維系統的多項式近似計算成為可能。以下簡要介紹左半張量積方法(右半張量積類似)。
1.1 左半張量積

1.2 多元多項式的半張量積表示

1.3 函數矩陣的微分


1.4 Taylor級數的半張量積表示

2 非線性系統及其多項式近似系統
2.1 非線性系統的多項式近似表示
考慮如下一般非線性系統

若f:Rm→Rm是一個解析映射,則根據半張量積方法,可對該非線性系統模型作n階Taylor展開,得到多項式近似系統如下
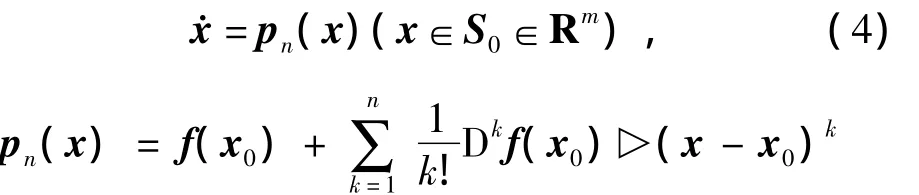
式中:x0表示展開點;Dkf(x)表示f(x)在x0處的k階偏微分;S0表示系統(3)Taylor級數的收斂域。
2.2 基本假設
設非線性系統(3)中f:Rm→Rm為解析函數,首先給出如下兩個假設
假設1 設閉集S是f(x)的Taylor級數的收斂域的閉子集,即S?S0;再令Ωz為系統(3)的平衡點的集合,即 Ωz:={x|f(x)=0,x∈Rm},則 Ωz∈S。
滿足假設1的條件下,f(x)在平衡點x*∈Ωz處的Taylor展開在S中是收斂的。此時,f(x)在穩定平衡點xsep處的n階Taylor展開為
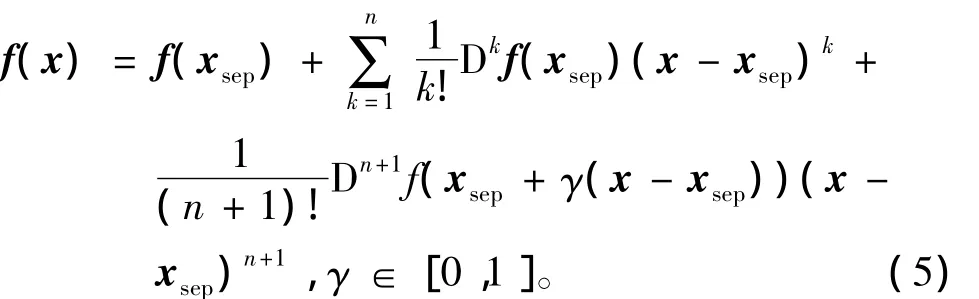
此外,滿足假設1時,Taylor展開式(5)的各階系數均一致有界。在高維條件下,即存在M>0,對任意k=1,2,…,有‖Dkf(x)‖∞≤M,其中‖·‖∞表示無窮范數,以下簡寫為‖·‖。
對式(5),分別令
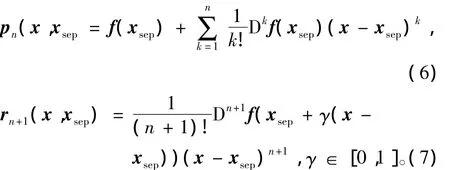
稱pn(x,xsep)為f(x)在 xsep處的n階 Taylor展開近似,稱 rn+1(x,xsep)為 f(x)在 xsep處的n階 Taylor展開近似的Lagrangian余項。則f(x)可表示為
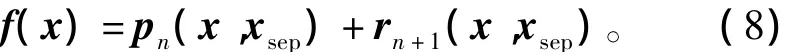
假設2 對?x∈S,有det(Df(x))≠0。
假設2的條件要求,對?x∈S,系統(3)的雅克比矩陣保持非奇異。通常情況下,由于系統(3)的雅克比矩陣的奇異點構成的集合在定義域內測度為零,因此該條件一般可以滿足。
2.3 基本引理


3 多項式近似系統與原系統平衡點的距離
利用多項式近似系統研究原系統,首先要研究二者之間平衡點的關系。下面從理論上證明近似系統平衡點與原系統平衡點可以任意接近,對此,我們給出如下定理。
定理1 考慮系統(3)滿足假設1、2,x*為系統的一個孤立平衡點,是系統(3)在穩定平衡點xsep處的多項式近似系統˙x=pn(x,xsep)的孤立平衡點,xsep,x*,xsep∈int(S)。則對?ε>0,?N∈Z+以及,使得n>N時,有‖xn*-x*‖< ε。


定理1表明,在滿足假設1、2的條件下,只要多項式近似的階數足夠高,在原系統孤立平衡點附近必然會出現一個近似系統的平衡點,進一步,隨著近似階數的增高,該平衡點會越來越趨近于原系統的平衡點,因此可以用近似系統˙x=pn(x,xsep)的平衡點來逼近原系統˙x=f(x)的孤立平衡點x*。
此外,從定理的證明過程可以看出,假設2僅僅是定理1成立的一個充分條件,事實上并不需要S上所有的點都滿足雅克比矩陣非奇異的要求,而只需要其中相關的某些點處滿足,定理1即可成立。
4 多項式近似系統與原系統平衡點的類型
為了利用近似系統研究原系統,除了要保證近似系統與原系統平衡點任意接近外,還要保證二者之間性質一致。下面從理論上證明當近似階數足夠時,近似系統不穩定平衡點與原系統不穩定平衡點類型可保持一致,即不穩定平衡點拓撲性質不變。
首先給出如下一些引理。
引理3[16]對于一個多項式系統,可通過同倫路徑法確定其全部實根。
引理 4[16]令 u=(x,λ),設構造的同倫路徑為H(u),則該同倫軌跡由如下的初值問題確定,即
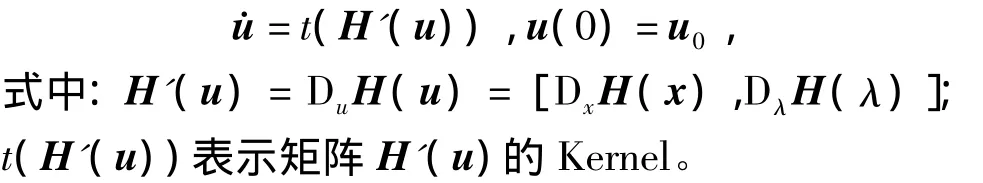
引理5[18]若兩平衡點在相同的λ面,則兩平衡點類型相差奇數;若兩平衡點在不同的λ面,則兩平衡點類型相差偶數。
引理6[16]若同倫路徑中存在拐點,則該同倫路徑兩端的平衡點類型改變,且類型的改變值等于拐點個數。
引理7[11]若H'(x)在連接兩個平衡點的整個同倫路徑中非奇異,則該同倫路徑中不存在拐點及分叉點,因而該同倫路徑兩端的平衡點類型一致。
根據引理3-引理7,我們有如下定理
定理2 對非線性系統(3),若假設1、2滿足,設xuep為˙x=f(x)的一個孤立的雙曲k型不穩定平衡點,其近似系統˙x=pn(x,xsep)相應的平衡點為xn-uep,則存在N∈Z+,當n>N時,xn-uep也為雙曲k型不穩定平衡點。
證明 構造同倫方程
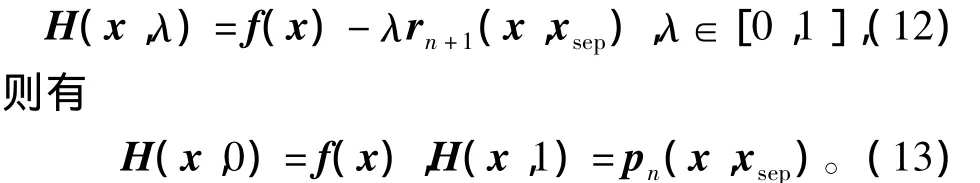
可知,若從˙x=f(x)的某一不穩定平衡點xuep出發,跟蹤同倫路徑,當 λ從0變化至1時,H(x,λ)從=f(x)的不穩定平衡點xuep運動至=pn(x,xsep)的平衡點xn-uep,其中 xn-uep=xuep+Δx,Δx為近似系統平衡點xn-uep與原系統平衡點xuep之間的誤差。
根據引理7可知,若整個同倫路徑中,H'(x)=DH(x)保持非奇異,則該同倫路徑中不存在拐點及分叉點,因此同倫路徑兩端的平衡點類型一致,即xn-uep與xuep類型一致。
由假設1知,對?x∈S,Df(x)非奇異(即 det(Df(x))≠0),由Df(x)的連續性可知,若在Df(x)上施以足夠小的擾動時,Df(x)仍保持非奇異,即
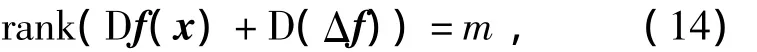
因此只需證明,當近似階數足夠高時,D(Δf)可以足夠小即可。
由式(12)可知
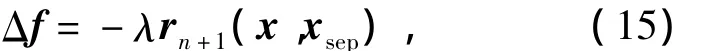
即是要證明當近似階數足夠高時,‖Drn+1(x,xsep)‖可以足夠小。根據引理2的證明過程可知,這一結論成立。當選取充分大的n時,我們總可以使得‖Drn+1(x,xsep)‖足夠小,從而使得DH(x)=Df(x)-λDrn+1(x,xsep)在整個同倫路徑中保持非奇異;因此,從xuep到xn-uep的整個同倫路徑中不存在拐點及分叉點,從而保證同倫路徑兩端的平衡點類型一致,即xn-uep與xuep類型一致。證畢。
定理2從理論上保證了在一定條件下,當近似階數足夠高時,近似系統與原系統平衡點附近的拓撲性質可以保持一致。
通過以上定理,我們可以得出結論:當近似階數足夠高時,近似系統平衡點可以與原系統平衡點任意接近且類型保持一致,因此我們可以用多項式近似系統來研究原系統的平衡點及穩定域邊界。
5 結論
利用半張量積方法求得一般非線性系統的多項式近似表達,并在理論上證明:當近似階數足夠高時,多項式近似系統與原系統平衡點可任意接近且類型保持一致,從而為利用多項式近似系統來研究原系統的平衡點及其穩定性提供了理論基礎。本文提出的理論結果在電力系統穩定性分析中的一些初步應用工作將在下一篇論文中介紹。
[1]CHIANG Hsiao-Dong,WU F F,VARAIYA P P.A BCU method for direct analysis of power system transient stability[J].IEEE Transactions on Power Systems,1994,9(3):1194 -1208.
[2]SCRUGGS J T,MILI L,Dynamic gradient method for PEBS detection in power system transient stability assessment[J].Int.Journal of Electrical Power&Energy Systems,2001,23(2):155-165.
[3] TREINEN R T,VITTAL V,KLIEMANN W.An improved technique to determine the controlling unstable equilibrium point in a power system[J].IEEE Transactions on circuits and systems-I:Fundamental Theory and Applications,1996,43(4):313 -323.
[4]NAZARENO I S,ALBERTO L F C,BRETAS N G.Problems in the precise detemination of BCU’s controlling unstable equilibrium points and PEBS’s exit point method in real-time transient stability analysis[C]∥IEEE/PES Transmission&Distribution Conference&Exposition.Latin America:IEEE,2004:475-480.
[5]NAZARENO I S,ALBERTO L F C,BRETAS N G.Robust computation of the controlling unstable equilibrium points in transient stability analysis[C]∥Power Tech.Russia:IEEE,2005:1-7.
[6]LEE J,CHAING H D.Computation of multiple type-one equilibrium points on the stability boundary using generalized fixed-point homotopy methods[C]∥Proceedings of the2001IEEE International Symposium on Circuits and Systems.Sydney:ISCAS,2001,3:6-9.
[7]LEE J,CHIANG H D.Convergent regions of the Newton homotopy method for nonlinear systems:theory and computational applications[J].IEEE Transactions on Circuits and Systems I:Fundamental Theory and Applications,2001,48(1):51-66.
[8]LEE J,CHIANG H D.A singular fixed-point homotopy method to locate the closest unstable equilibrium point for transient stability region estimate[J].IEEE Transactions on Circuits and Systems II:Express Briefs,2004,51(4):185 -189.
[9]侯凱元,閔勇.基于伴隨系統理論的電力系統主導不穩定平衡點求解方法[J].現代電力,2005,22(1):21-26.
HOU Kaiyuan,MIN Yong.Computing the controlling unstable equilibrium point based on the theory of adjoint systems[J].Modern Electric Power,2005,22(1):22 -26.
[10]CHIANG Hsiao-dong,CHU Chia-chi,CAULEY Gerray.Direct stability analysis of electric power systems using energy functions:theory,applications and perspective[J].Proceedings of the IEEE,1995,83(11):1497-1529.
[11]COX D A,LITTLE J,O’SHEA D.Using Algebraic Geometry[M].Berlin:Springer,2005:69-76.
[12]BENALLOU A.MELLICHAMP D,SEBORG D.On the number of solutions of multivariable polynomial systems[J].IEEE Transactions on Automatic Control,1983,28(2):224 -227.
[13]MORGAN A.Solving Polynomial Systems Using Continuation for Engineering and Scientific Problems[M].Englewood Cliffs,N J:Prentice-Hall,1987:Ⅸ -Ⅹ.
[14]劉安心.求多項式方程組全部解的連續法[J].工程兵工程學院報,1999,14(1):80-85.
LIU Anxin.Continuation method of solving all solutions of polynomial equations[J].Journal of Engineer Corps and Egineering Institute,1999,14(1):80 -85.
[15]LI Tien-Yien,Chih-Hsiung Tsai.HOM4PS-2.0 para:parallelization of HOM4PS-2.0 for solving polynomial systems[J].Parallel Computing,2009,35(4):226-238.
[16]ALLGOWER E L,GEORG K.Numerical Continuation Methods[M].Berlin:Springer-Verlag,1990:7-16.
[17]程代展.矩陣的半張量積理論與應用[M].北京:科學出版社,2007:1-134.
[18]GRIEWANK A,REDDIEN G W.Characterization and computation of generalized turning points[J].SIAM J.Numer.Anal.,1984,21(1):176-185.
(編輯:張 靜)
- 電機與控制學報的其它文章
- 直升機旋轉逆動力學建模及姿態控制研究

