相空間法對混沌序列的自相關(guān)特性研究
陳 濱 ,劉光祜,唐 軍,張 勇,蔡 鵬,黃 堅,吳云松
(1. 江西財經(jīng)大學軟件與通信工程學院 南昌 330013; 2. 電子科技大學電子工程學院 成都 610054)
相空間法對混沌序列的自相關(guān)特性研究
陳 濱1,劉光祜2,唐 軍1,張 勇1,蔡 鵬1,黃 堅1,吳云松1
(1. 江西財經(jīng)大學軟件與通信工程學院 南昌 330013; 2. 電子科技大學電子工程學院 成都 610054)
混沌序列已作為偽隨機序列得到廣泛應用,但如何判斷混沌序列的相關(guān)特性、調(diào)制后相關(guān)特性的好壞,以及其理論依據(jù),至今尚無定論,使其應用受到限制。該文給出了判斷混沌序列自相關(guān)特性好壞的一個簡單有效的方法。用相空間法對混沌序列的自相關(guān)特性作了研究,發(fā)現(xiàn)相空間軌跡是否具有軸對稱性與其自相關(guān)函數(shù)好壞相對應,證明了相空間軌跡具有軸對稱結(jié)構(gòu)的序列有好的自相關(guān)函數(shù),并通過仿真予以了證實。
自相關(guān); 混沌映射; 相空間; 偽隨機序列; Tent映射
混沌序列具有類隨機性[1-6],近來已作為偽隨機序列在保密通信、雷達等方面得到廣泛應用[3-18]。但混沌序列的自相關(guān)問題,以及在各種調(diào)制方式下的調(diào)制后信號自相關(guān)問題,長久以來沒有得到解決,導致混沌序列在應用中受到諸多限制。
近來大量文獻[1-11,18]欲將混沌序列作為噪聲源用于噪聲雷達。但有一些混沌序列,本身自相關(guān)特性差;還有一些混沌序列,雖然本身自相關(guān)特性好,但經(jīng)過調(diào)制后,自相關(guān)性能大幅下降[3-6],對雷達信號的準確檢測和識別很不利,引起學術(shù)界對混沌序列自相關(guān)特性及調(diào)制后自相關(guān)特性的關(guān)注[2-7]。
本文就混沌序列的自相關(guān)問題進行探討。利用相空間方法,證明了相圖軌跡具有對稱結(jié)構(gòu)的混沌序列具有好的自相關(guān)函數(shù)。
1 混沌序列的相關(guān)性問題
性能良好序列的自相關(guān)函數(shù)的波形應為一根尖細的針形,沒有突出的副瓣,實際運用起來才有利于信號的準確檢測和識別。如圖1所示的Tent序列的自相關(guān)函數(shù),主峰尖細,副瓣很低,以至于在圖上看不到,性能很好。Tent序列自相關(guān)函數(shù)性能雖然很好,但經(jīng)過隨機頻率調(diào)制(random frequency modulation,RFM)后,自相關(guān)函數(shù)變差,如圖2所示,副瓣很多很高,性能變差。Bernoulli序列的自相關(guān)函數(shù)曲線如圖3所示,其主峰比較粗,性能較差。因此,不僅混沌序列的自相關(guān)特性有差異,經(jīng)過調(diào)制后自相關(guān)特性也可能出現(xiàn)差異。
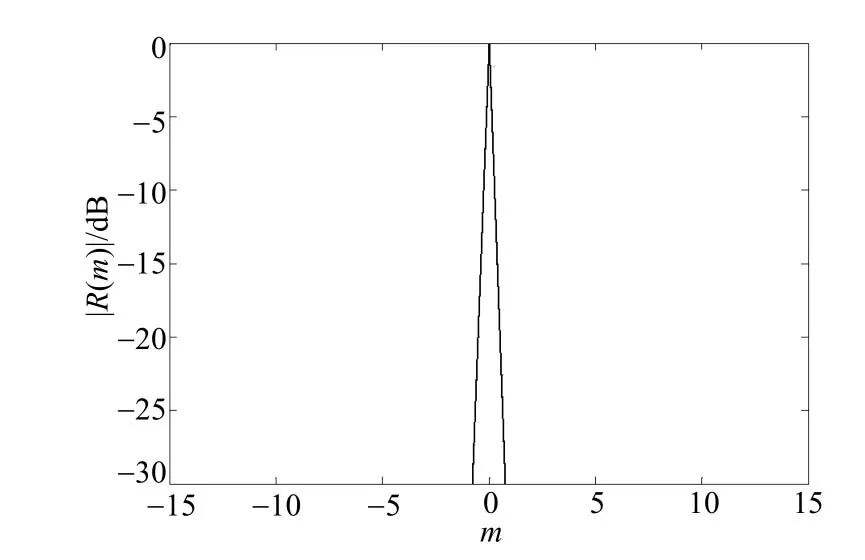
圖1 Tent序列調(diào)制前的歸一化自相關(guān)函數(shù)
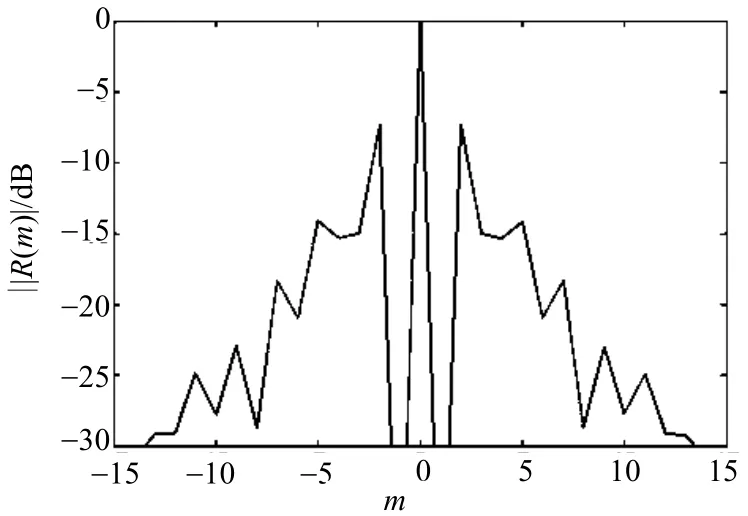
圖2 Tent 序列調(diào)制后的歸一化自相關(guān)函數(shù)
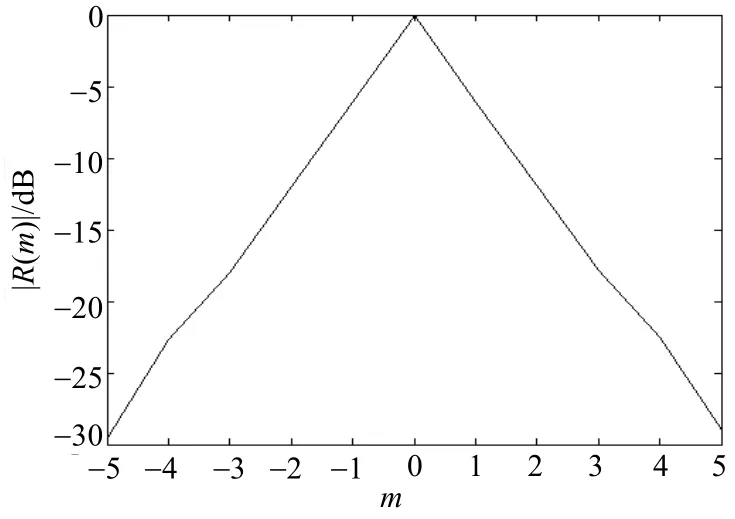
圖3 Bernoulli序列歸一化自相關(guān)函數(shù)
2 混沌序列的二維相空間及自相關(guān)函數(shù)

對于長度為N平穩(wěn)且遍歷的序列{x(n)},其自相關(guān)函數(shù)r(m)為:

Tent序列的歸一化自相關(guān)函數(shù)性能好,即自相關(guān)函數(shù)的波形為一根尖細的針形,沒有突出的副瓣;Bernoulli序列的自相關(guān)函數(shù)主峰比較粗大,性能較差,不利于信號檢測。下面通過證明4個定理,研究它們自相關(guān)函數(shù)性能差異的原因。
3 序列二維相圖與自相關(guān)特性的聯(lián)系

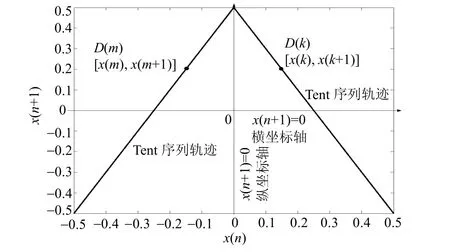
圖4 Tent序列延遲1相圖
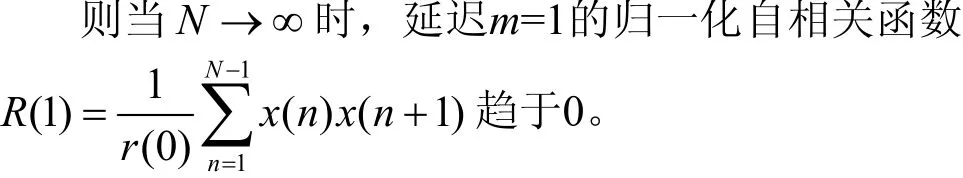
證明 因為序列平穩(wěn)遍歷,均值為0,且延遲1的相圖軌跡依縱坐標軸對稱,圖4為Tent序列延遲為1的相圖。因此可在延遲1相圖軌跡上任取關(guān)于縱軸對稱的兩點D(k)、D(j),其中D(k)的坐標為[x1(k),x1(k+1)],D(j)的坐標為[x1(j),x1(j+1)],且有x1(j)=?x1(k),x1(k+1)=x1(j+1)。

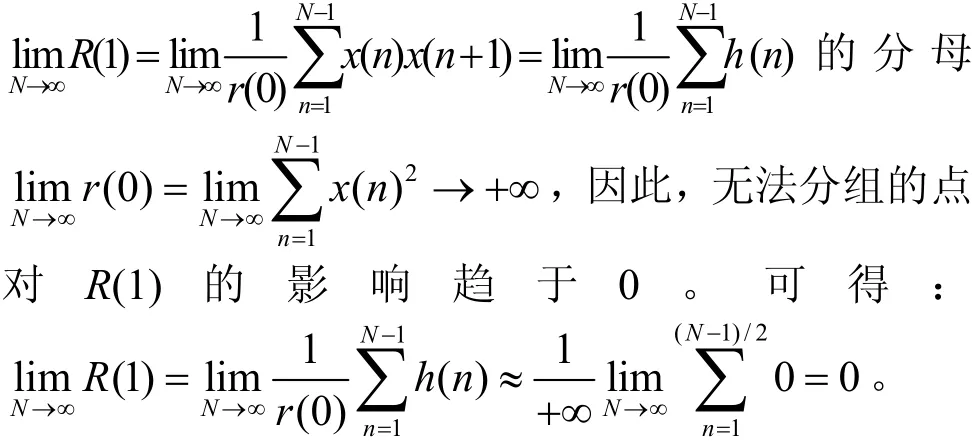
原命題得證。
如圖4所示,Tent序列延遲1的相圖。其吸引子軌跡對縱坐標軸x(n)=0對稱,則由定理1,其歸一化自相關(guān)函數(shù)R(1)應趨近于0。圖5表示N=2 000的Tent序列的歸一化自相關(guān)函數(shù),R(1)趨近于0,與定理1相符。用Logistic序列等其他序列檢驗,可得同樣結(jié)論。
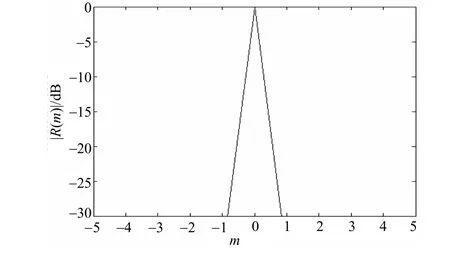
圖5 Tent序列的歸一化自相關(guān)函數(shù)
對于延遲1的相圖軌跡,依橫坐標軸對稱的情況,有定理2。

定理2的證明與定理1的證明類似,不在此贅述。定理2中對橫坐標軸對稱的動力系統(tǒng),可以用動力系統(tǒng)的每步演化值,由概率0.5乘以(?1)得到。對Bernoulli序列作上述處理,處理后序列的歸一化自相關(guān)函數(shù)R(1)趨近于0,與定理2相符。
綜上所述,離散動力系統(tǒng)延遲為1的相圖,無論對橫軸,或縱軸,亦或是同時對橫、縱坐標軸統(tǒng)計對稱,都可得其歸一化自相關(guān)函數(shù)R(1)趨近于0。因此,有以下結(jié)論成立。
結(jié)論 對于一個平穩(wěn)遍歷的離散實動力系統(tǒng):

其值域為[?a,a],a為正實數(shù);{x(n)}的均值0,且取值的正負具有統(tǒng)計平衡性。

其值域為[?a,a],a為正實數(shù);{x(n)}的均值為0,且取值的正負具有統(tǒng)計平衡性。
若{x(n)}的延遲為1的相圖軌跡在統(tǒng)計意義上對橫坐標軸;或?qū)v坐標軸對稱,或?qū)M、縱坐標軸都對稱。
則{x(n)}除0外的任意延遲的相圖軌跡,在統(tǒng)計意義上也對該坐標軸對稱。
證明先證明延遲1相圖軌跡對縱軸統(tǒng)計對稱的條件下,延遲為2的相圖軌跡依然對縱軸統(tǒng)計對稱。

即g[D(k)]= g[D(j)],關(guān)于D(k)、D(j)分布的概率密度依然相等。因此,延遲2相圖軌跡依然對縱軸統(tǒng)計對稱。
同理可得,除0外的任意延遲的相圖軌跡,在統(tǒng)計意義上也對縱坐標軸對稱。
對延遲1相圖軌跡對橫坐標軸對稱的情況,同理可得,除0外的任意延遲的相圖軌跡,在統(tǒng)計意義上也對橫坐標軸對稱。
綜上所述,延遲為1的相圖軌跡,在統(tǒng)計意義上對橫坐標軸,或?qū)v坐標軸對稱,或同時對橫、縱坐標軸對稱的條件下,可得除0外的任意延遲的相圖軌跡,在統(tǒng)計意義上也對橫坐標軸,或?qū)v坐標軸對稱,或同時對橫、縱坐標軸對稱。
原命題得證。

綜合前述結(jié)論及定理3,定理4得證。
從前述的Tent序列,可以檢驗定理4的正確性。Tent序列滿足定理4的條件,則除m=0外的歸一化自相關(guān)函數(shù)R(m)都趨近于0,如圖5所示,與定理4相符。考察Logistic序列等其他滿足定理4條件的序列,可得同樣的結(jié)論。
考察不滿足定理4條件的序列,如圖6所示N=2 000的Bernoulli序列的延遲1相圖,其軌跡既不關(guān)于橫坐標軸對稱,也不關(guān)于縱坐標軸對稱,圖3表示其歸一化自相關(guān)函數(shù),可見當|m|=1,2,3,4,5時,R(m)都較大,不趨近于0,自相關(guān)函數(shù)性能差。
至此,找到了Tent、Bernoulli序列自相關(guān)函數(shù)性能差異的原因。
定理4是針對動力系統(tǒng)而言,但可以推廣到其他序列,如噪聲序列等。
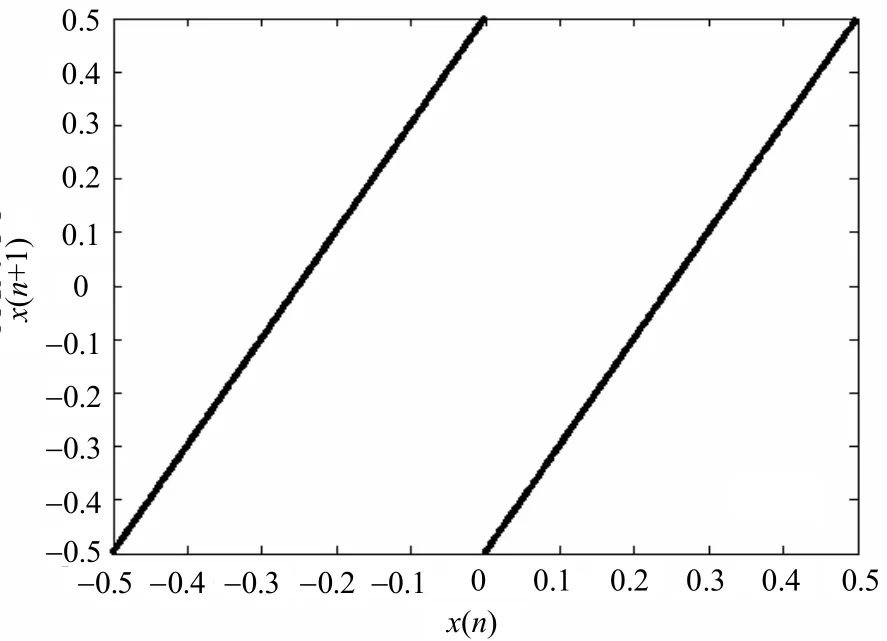
圖6 Bernoulli序列延遲1相圖
4 定理4的實質(zhì)
由定理4可知,判斷一個取值平衡的序列自相關(guān)特性,只需要在其延遲1的二維相圖上,檢驗軌跡對坐標軸的統(tǒng)計對稱性,若其對橫或縱坐標軸統(tǒng)計對稱,或?qū)M、縱兩坐標軸都統(tǒng)計對稱,則其自相關(guān)特性較好,即具有突出的主峰,沒有高的旁瓣。前面用Tent序列和Bernoulli序列檢驗了定理4的正確性。此外,本文還檢驗了很多其他序列,都與定理4相符。
相圖是反映一個動力系統(tǒng)內(nèi)在本質(zhì)的一種工具,由它可以得知動力系統(tǒng)的結(jié)構(gòu)。一般來說,延遲1的二維相圖,相對于其他更大延遲相圖而言,結(jié)構(gòu)最為簡單、清晰。通過判斷延遲1相圖軌跡的對稱性辨別序列相關(guān)性的方法,是簡單和實用的方法。
使序列取值正負平衡,是比較容易的。常見的混沌序列,如Tent序列、Bernoulli序列、Logistic序列、Chua序列、MSPL(multi-segment piecewise linear)序列[5]等,都可以滿足,或簡單處理后滿足取值正負平衡。
5 結(jié)論及展望
本文利用相空間方法證明了一個取值平衡序列,若其延遲1的相圖軌跡具有坐標軸對稱結(jié)構(gòu),則其自相關(guān)函數(shù)具有較好的特性。該結(jié)論以定理4的形式給出。在后續(xù)研究中,將對本文結(jié)論(即定理4)的更多運用和序列的調(diào)制相關(guān)性進行探討。
[1]GAMBI E, CHIARALUCE F, SPINSANTE S. Chaos-based radars for automotive applications: Theoretical issues and numerical simulation[J]. IEEE Transactions on Vehicular Technology, 2008, 57(6): 3858-3863.
[2]SUNE R J. Noise radar using random phase and frequency modulation[J]. IEEE Trans Geosci Remote Sens, 2004,42(11): 2370-2384.
[3]FLORES B C, SOLIS E A, THOMAS G. Assessment of chaos-based FM signals for range-doppler imaging[J]. IEE Proc-Radar Sonar Navig, 2003, 150(4): 313-322.
[4]FLORES B C, SOLIS E A, THOMAS G. Chaotic signals for wideband radar imaging[C]//Proc SPIE-Int Soc Opt Eng.Orlando, Fl, USA: Proc SPIE, 2002, 4727: 100-111.
[5]陳 濱, 周正歐, 劉光祜, 等. 混沌噪聲源在噪聲雷達的應用[J]. 現(xiàn)代雷達, 2008,30(5): 24-28.
CHEN Bin, ZHOU Zheng-ou, LIU Guang-hu, et al.Application of chaos series as noise source in noise radar[J].Modern Radar, 2008, 30(5): 24-28.
[6]CHEN Bin, TANG Jun, ZHANG Yong, et al. Chaotic signals with weak-structure used for high resolution radar imaging[C]//CMC 2009. Kunming, Yunnan: IEEE Press,2009, 1: 325-330.
[7]MYERS J, FLORES B C. Radar imaging via random FM correlations[C]//Proc SPIE-Int Soc Opt Eng. Orlando, Fl,USA: Proc SPIE, 1999, 3721: 130-139.
[8]VIJAYARAGHAVAN V, HENRY L. A novel chaos-based high-resolution imaging technique and its application to through-the-wall imaging[J]. IEEE Signal Processing Letters,2005, 12(7): 528-531.
[9]XU Y, NARAYANAN R M, XU X, et al. Polarimetric processing of coherent random noise radar data for buried object detection[J]. IEEE Trans Geosci Remote Sens, 2001,39(3): 467-478.
[10]GU H, LIU G, ZHU X, et al. A new kind of noise-radar random binary phase coded CW radar[C]//Proc IEEE National Radar Conf Syracuse. NY, USA: IEEE Press,1997: 202-206.
[11]WU X, LIU W, ZHAO L, et al. Chaotic phase code for radar pulse compression[C]//Proc IEEE National Radar Conf. Atlanta, GA, USA: IEEE Press, 2001: 279-283.
[12]DAWOOD M, NARAYANAN R M. Ambiguity function of an ultrawideband random noise radar[C]//Proc IEEE Antennas and Propagation Soc Int Symp. Salt Lake City,UT, USA: IEEE Press, 2000: 2142-2145.
[13]楊亞濤, 王曼珠, 張喆民. 超混沌序列的數(shù)字語音擴頻調(diào)制研究[J]. 電子科技大學學報, 2007, 36(4): 699-702.
YANG Ya-tao, WANG Man-zhu, ZHANG Zhe-min. Research on digital sound spreading-frequency modulation based on hyperchaos sequence[J]. Journal of University of Electronic Science and Technology of China, 2007, 36(4): 699-702.
[14]鐘黔川, 朱清新, 張平莉. 參數(shù)可變的多混沌映射加密系統(tǒng)[J]. 電子科技大學學報, 2009, 38(4): 274-277.
ZHONG Qian-chuan, ZHU Qing-xin, ZHANG Ping-li.Multiple chaotic maps encryption system[J]. Journal of University of Electronic Science and Technology of China,2009, 38(4): 274-277.
[15]CHON K H, KANTERS J K, IYENGAR N, et al.Detection of chaotic determinism in stochastic short time series[C]//IEEE/EMBS Proc 19th International Conference.Chicago, IL, USA: IEEE Press, 1997: 275-277.
[16]BUCOLO M, CAPONETTO R, FORTUNA L, et al. Does chaos work better than noise? [J]. Circuits and Systems Magazine, IEEE, 2002, 2(3): 4-19.
[17]JOSE A R, EDUARDO R, JUAN C E, et al. Correlation analysis of chaotic trajectories from Chua’s system[J].Chaos, Solitons and Fractals, 2008, 36(5): 1157-1169.
[18]LIU Z, ZHU X H, HU W, et al. Principles of chaotic signal radar[J]. International Journal of Bifurcation and Chaos in Applied Sciences and Engineering, 2007, 17(5): 1735-1739.
編 輯 張 俊
Research on Chaotic Sequence Autocorrelation by Phase Space Method
CHEN Bin1, LIU Guang-hu2, TANG Jun1, ZHANG Yong1, CAI Peng1, HUANG Jian1, and WU Yun-song1
(1. School of Software and Communication Engineering, Jiangxi University of Finance and Economy Nanchang 330013;2. School of Electronic Engineering , University of Electronic Science and Technology of China Chengdu 610054)
Chaotic sequences have been widely used as pseudorandom sequences. But the problem of how to judge the performances of their autocorrelation functions, up to now, has not yet been solved completely. Because of this, the applications of chaotic sequences are limited. In the paper, by method of phase space, we prove that the autocorrelation performance of a chaotic sequence is determined by whether its phase space trajectory is axis symmetrical, and we deduce a theorem that a sequence which phase space trajectory is axis symmetrical has good autocorrelation performance. The theorem is verified by simulations.
autocorrelation; chaotic map; phase space; pseudorandom sequence; Tent map
TN958
A
10.3969/j.issn.1001-0548.2010.06.012
2009- 05- 04;
2010- 01- 18
江西省教育廳科技基金(GJJ09286, GJJ09553, GJJ09554)
陳 濱(1971- ),男,博士生,主要從事混沌及其在雷達和通信中應用的研究.

