干擾因素對機動彈頭落點散布影響的計算方法研究

楊 寧，譚守林，劉曉亮

（第二炮兵工程學院，陜西西安 710025）

導彈在再入飛行過程中，存在著諸多干擾因素。由于干擾因素的影響，使彈頭機動再入的實際彈道，偏離預先計算的標準彈道，引起彈頭的實際落點偏離預定落點，從而產生落點偏差。這些干擾因素，將使得彈頭產生落點偏差。本文主要討論各種干擾因素對再入機動彈頭落點散布的影響。

1 再入機動彈道數學模型的構建

導彈在末段機動飛行的彈道，相對全程彈道來說，所占比例比較小，飛行時間較短。為了方便研究，在不考慮地球旋轉和扁率影響，可以假設地球為不旋轉的均質圓球，將質心動力學方程投影到軌跡坐標系中，在軌跡坐標系中建立的平面再入機動彈道數學模型為

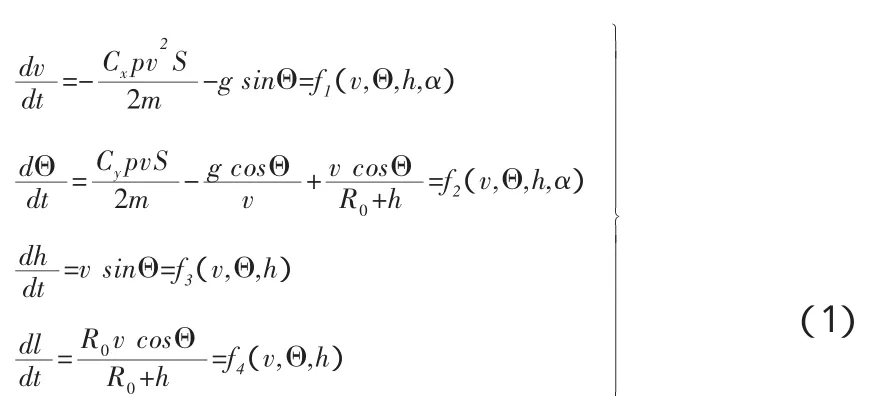
式中，

v、Θ、h和L分別為速度、當地彈道傾角、高度和機動射程；

m為彈頭質量；

S為彈頭最大橫截面積；

ρ為空氣密度；

Cx、Cy分別為空氣阻力系數和升力系數。

2 機動再入落點散布計算方法

通常將落點偏差分解為縱向偏差和橫向偏差，將彈頭的實際落點相對于理論落點的散落分布現象，稱為落點散布。影響彈頭機動再入落點散布的因素比較多，干擾因素獨立作用時的落點散布，可通過最大偏差法計算；然而，彈頭實際飛行中各干擾因素并非單獨存在，而是共同作用，有諸多因素的綜合影響時，通常采用蒙特卡洛法進行計算。

2.1 干擾因素獨立作用時落點散布的計算方法

彈頭機動再入過程中，影響落點散布的因素客觀存在，且各因素的表現值又具有隨機性，可認為各干擾因素之間是相互獨立的，因而每項因素的影響可以獨立計算。

利用最大偏差法計算干擾因素獨立作用時的落點散布，首先在機動初始條件下，應用數值積分法求解標準彈道，然后根據每一項干擾因素的大小，分別加入彈道模型中，取其偏差的最大值進行數值積分，計算結果與標準彈道計算結果進行比較，即可得到各項干擾因素造成的落點最大偏差。

每項干擾因素分別進行獨立計算，可以直觀看出干擾對落點參數影響的程度，進而可求出各因素獨立作用時的落點散布。

若有n項干擾因素，每項因素獨立計算得到的落點最大偏差為ΔLimax、ΔHimax（i=1,2,…，n），則彈頭機動再入總的落點偏差最大值為

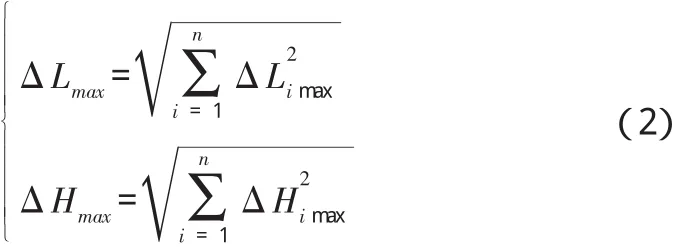
通常定義最大偏差是彈著點以99.306%的概率出現在其區域長度的一半，因此根據ΔLmax、ΔHmax可求出公算偏差值為

3.2 干擾因素綜合影響時落點散布的計算方法

彈頭機動再入過程中，多種干擾因素同時存在，是一種綜合影響。干擾因素綜合影響時，落點散布的計算通常采用蒙特卡洛法。

蒙特卡洛法是一種試驗數學方法，其以概率統計理論為主要理論基礎，以隨機抽樣（隨機變量的抽樣）為主要手段，利用隨機數進行統計檢驗，以求得的統計特征值（如均值、方差、概率等）作為待解問題的數值解。

用蒙特卡洛法計算彈頭機動再入過程中，干擾因素綜合影響時的落點散布的步驟為：

第一步，分析各種干擾因素，確定其分布，建立干擾偏差概率模型；

第二步，根據各干擾偏差出現的概率進行隨機抽樣；

第三步，將各干擾因素抽樣值代入彈道模型中進行求解，結果與標準彈道結果比較；

第四步，重復第二、三步直至得出落點偏差的大量樣本，然后利用數理統計理論進行統計分析。

建立概率模型是難度最大而又最關鍵的一步。所建的概率模型，要能正確反映各干擾因素的實際情況，使所求的解恰好是所建模型的概率分布或數學期望。要充分利用已有的地面試驗和飛行試驗的信息，積累和收集各干擾量的統計數據，加以適當處理，就可得到反映某種干擾因素的某隨機過程的一組觀測數據，若該觀測數據互相獨立，可采用隨機變量概率分布的建模方法，若觀測數據不獨立而相關，可采用時間序列分析法建模。

假設彈頭機動再入過程中有m個干擾因素，建立干擾偏差概率模型后進行隨機抽樣，產生n組隨機干擾源

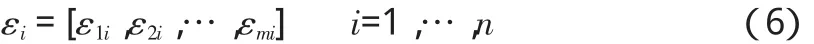
將每組隨機干擾源分別代入彈道模型中進行數值計算，求出在隨機干擾作用下的實際彈道，與標準彈道相比較，得到落點偏差的大量樣本 ΔL、ΔH（i=1，2，…，n），根據數理統計理論，得樣本均值為：

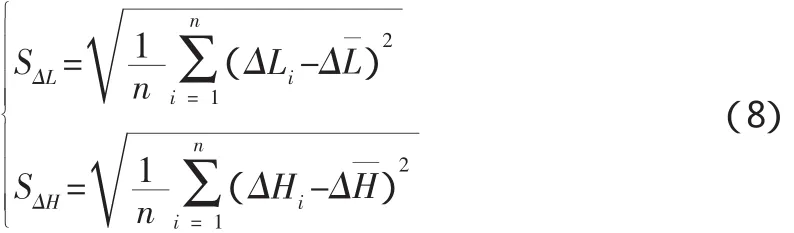
一般情況下，導彈落點偏差服從正態分布N（μe，σ2e），利用抽取的樣本對其進行點估計

得到了 μe、σe的估計量，就可采用式（3）和式（5）計算公算偏差及圓概率偏差。

在給定置信水平（1-α）下，對彈頭落點偏差的均值和方差進行區間估計。均值μe的置信區間，已知方差（σ2e=%σ2

0e）時為

3 機動再入落點散布計算及分析

3.1 落點散布計算

計算落點散布時，確定各干擾因素的偏差范圍，是最關鍵最復雜的問題。通常要通過地面試驗和飛行試驗的信息，進行分析處理才能確定。由于缺乏相關信息資料，本文依據某型彈頭再入參數偏差值，通過機動和非機動兩種情況下的落點散布進行比較，分析機動再入對落點散布的影響。這里主要討論7種干擾因素對落點散布的影響（如表1所示）。

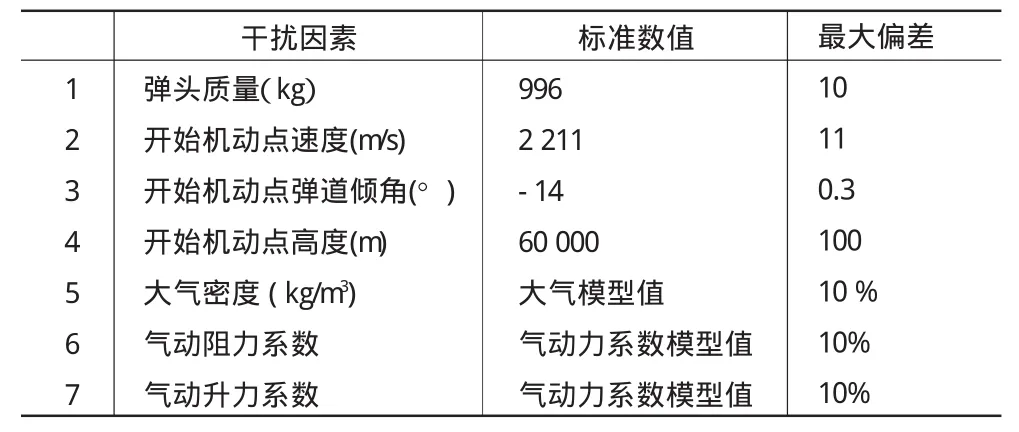
表1 計算落點散布時考慮的干擾因素及其干擾量

為計算方便，認為各干擾因素相互獨立，采用最大偏差法進行平面機動再入和非機動再入落點散布計算。由于是平面再入，所以橫向偏差為零，計算時只有縱向偏差，計算結果如表2所示。

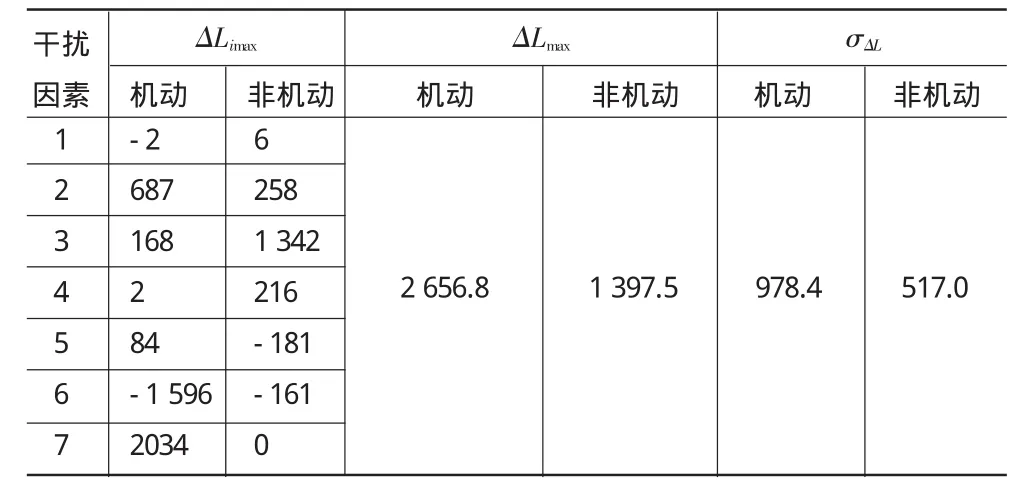
表2 平面再入落點散布 單位：m

3.2 落點散布分析

落點散布計算時，假設機動和非機動兩種情況在開始機動點前的彈道參數相同，而開始機動后一條彈道是機動彈道，另一條彈道為非機動的橢圓彈道，并且打擊同一目標，所受干擾相同。其目的是為了通過機動和非機動兩種情況下落點散布的比較，來反映機動再入對落點散布的影響程度，找出影響機動再入落點散布的主要因素，以便采取有效措施，減小主要因素的干擾或進行彈道修正，減小落點散布。

從表2看出，不帶末制導機動再入的落點散布，比非機動再入時大，彈道傾角偏差對非機動再入落點偏差的影響較大；而速度偏差和氣動力系數偏差，對機動再入落點散布影響較大；其余因素引起的落點偏差，比非機動再入時小得多。

因此，采用機動再入時，要采取措施減小速度偏差和氣動力系數偏差引起的落點偏差。一方面，要提高制導精度，采用末制導機動再入；另一方面，對彈頭進行防熱處理，減小彈頭再入過程中，因氣動燒蝕和侵蝕而引起氣動外形變化導致的氣動力系數偏差，或加強氣動燒蝕和侵蝕的研究，建立精確的氣動燒蝕和侵蝕數學模型。

5 結束語

導彈在機動飛行過程中，多干擾因素的單獨作用或者綜合作用，使得彈頭落點散布產生不同的偏差。運用蒙特卡洛法計算多干擾因素對彈頭落點散步影響是可行的。考慮干擾因素的影響，對于提高導彈武器系統打擊精度具有一定的參考價值。

[1]趙漢元.飛行器再入動力學和制導[M].長沙：國防科技大學出版社，1997.

[2]張 毅，楊輝耀，李俊莉.彈道導彈彈道學[M].長沙：國防科技大學出版社，1999.

[3]劉石泉.彈道導彈突防技術導論[M].北京：中國宇航出版社，2003.

[4]王 芳，劉新學.彈道導彈再入機動彈道設計研究[J].計算機仿真，2008，25（6）:59-61..

[5]周國峰，王朝志，陳萬春.機動彈頭引入段彈道優化設計[J].戰術導彈技術，2008，（5）:20-23.