基于神經網絡的機械系統可靠性評價模型

劉海年，謝里陽，張靜

（1.沈陽發動機設計研究所，沈陽110015；2.東北大學機械工程與自動化學院，沈陽110004）

1 引言

為了提高可靠性，有高可靠性要求的工業系統常常設計成冗余結構。然而在實際應用中，常常會出現2個或多個零件由于某種共同的原因而同時失效的情況(所謂的共因失效-相關失效的1種主要形式)，嚴重削弱了冗余結構的安全作用[1]。謝里陽教授提出了系統層的應力強度干涉模型[2]，在不做零件失效相互獨立的條件下，根據系統層的應力-強度干涉理論，可以推導出系統可靠度計算的概率表達式。然而，在實際工程問題中，一般很難確定組成系統的各零件的應力、強度分布及其概率密度函數，使得其應用受到限制。工程實際系統的可靠性預測多是以零件或系統的失效數據為基礎。因此，通過系統或零件間的失效數據來構建機械系統的可靠性評價模型成為人們研究的熱點。

本文主要研究復雜機械系統的可靠性預測問題，通過構建高階冗余系統，應用Monte-Carlo方法模擬不同條件下冗余系統的失效數據，得到1組基本變量及其對應的系統失效概率等響應輸出；充分利用BP神經網絡模型的函數逼近功能、非線性映像功能和容錯能力[3]，建立系統失效概率與零件失效數據之間的非線性關系，進而構建基于神經網絡的機械系統可靠性評價的參數化模型，從而可以獲得系統的任意階失效概率，為進行相關失效的系統可靠性評價提供了1種新方法。

2 人工神經網絡模型及BP算法

人工神經網絡是由大量簡單處理單元廣泛互連而成的網絡。BP網絡是當前應用最為廣泛的人工神經網絡，它是多層映像網絡，采用最小均方差的學習方法，結構簡單，工作狀態穩定，具有很強的非線性映像能力，可以用于建立復雜的非線性函數的近似映射模型[4,5]。

在進行訓練時，每1個輸入-輸出模式對在網絡中經過2遍傳遞計算。1遍進行正向傳播計算，從輸入層開始傳遞到各層，經過處理后產生1個輸出，并得到1個該實際輸出和所需輸出之差的差錯向量；1遍進行反向傳播計算，從輸出層至輸入層，利用差錯向量對連接權值和閾值進行逐層修改。

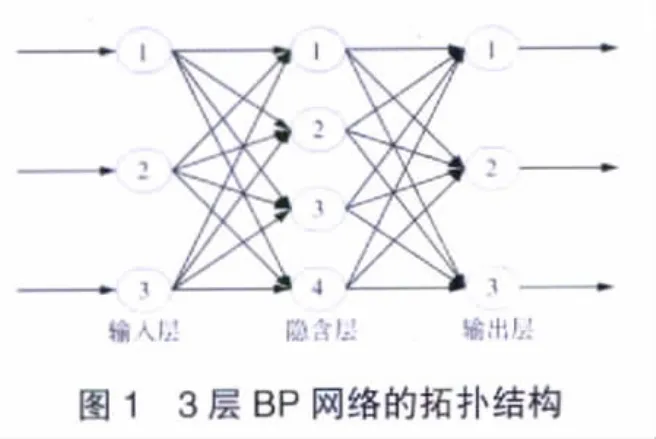
經過訓練學習好的BP網絡即可應用。學習后的網絡其連接權值和閾值均已確定，即構建BP網絡模型。BP模型可以被看成為1個從輸入到輸出的映射，而且此映射是1個高度非線性的映射。關于BP網絡的映射能力，許多人進行過研究，已經被總結成為“BP定理”[6]。該定理表明，假定BP網絡中隱節點可以根據需要自由設定，那么，對于任何在閉區間內的1個連續函數都可以用含有1個隱含層的BP網絡來逼近，因而1個3層的BP網絡可以完成任意精度要求的n維到m維的映射。圖1示出了3層BP神經網絡模型，由輸入層、1層隱含層和輸出層組成。由此可知，通過BP網絡可以把復雜系統零件的失效數據基本變量和系統失效概率響應之間復雜的、無法用顯式表達的函數關系建立起來，用于系統失效概率的仿真計算。

3 Monte-Carlo仿真K/N系統可靠性

在可靠性工程中，經常遇到處理隨機變量函數的問題，通常使用蒙特卡羅方法來仿真系統的可靠性，獲得相應的可靠性指標[2]。本文使用該方法模擬K/N系統可靠性，產生系統的失效數據，作為網絡的訓練數據。

蒙特卡羅方法求解問題的基本步驟如下。

（1）確定隨機變量的分布形式。隨機變量的分布形式通常可以由試驗方法獲得，本文假設組成系統的各零件所承受的應力和強度服從威布爾分布函數，這主要因為，在機械工程中威布爾分布在可靠性領域內運用的越來越多，可以用來描述載荷分布及壽命分布等。

（2）產生[0,1]區間上均勻分布的偽隨機數，利用MATLAB軟件自帶的隨機數發生器函數rand()生成的含有106隨機數[7]。

（3）對偽隨機數進行參數、均勻性和獨立性檢驗[8]。事實證明，這些隨機數可以代表隨機變量的特性，從而可以進行系統的仿真。

（4）利用偽隨機數生成服從威布爾分布的隨機變量。根據隨機抽樣的反變換法可知，要產生服從F(x)的隨機數，需要產生服從[0,1]區間上均勻分布的隨機數r，然后計算F-1(r)即可獲得[8]。設變數r～U(0,1)，零件強度的隨機變量S～W(β,θ,α)，其中β為形狀參數，α為位置參數，θ為尺度參數。令r=F(S)，反解S得

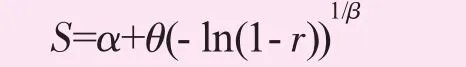
那么隨機變量S～W(β,θ,α)。同理，可以獲得服從威布爾分布的零件載荷s的分布，即可進行系統可靠性仿真。

（5）仿真K/N系統可靠性。本文主要考慮不同應力不同零件條件下K/N系統的可靠性仿真模型，為此做出以下假設：

a.假設構成系統的零件具有不同的強度分布函數。

b.考慮系統的相關性，組成系統的各零件處于同一載荷環境的共同作用下，但具有不同的應力分布函數。

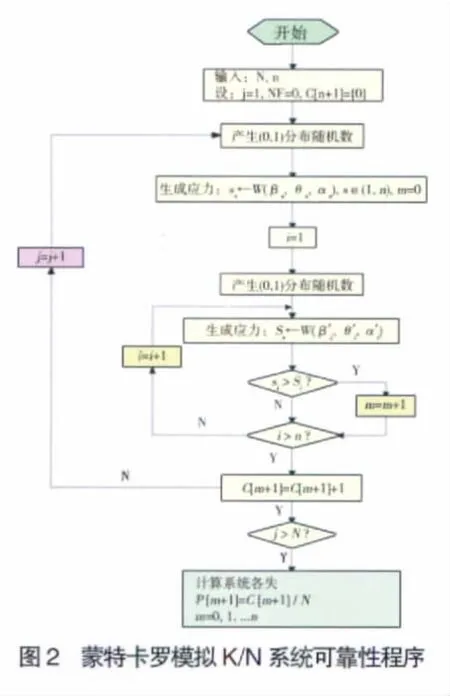
K/N系統可靠性的仿真框圖如圖2所示。

4 基于BP網絡的K/N系統可靠性模型

基于神經網絡的K/N系統可靠性模型構建的過程如下。

（1）獲取神經網絡訓練樣本。由于在實際工程系統中很難獲得系統的高階失效數據，因此本文通過上述的蒙特卡羅方法模擬冗余系統的可靠性，產生神經網絡模型的訓練樣本。在冗余系統中，通過n次更改系統的零件個數、零件的應力、強度等參數，輸入到構建的冗余系統模型中，獲得n個對應不同系統失效階數的失效概率，這n組數據值與失效概率即可作為人工神經網絡的組訓練樣本和測試樣本集。

（2）建立神經網絡模型。根據謝里陽教授提出的系統層的載荷-強度干涉模型[2]，作者認為系統零件個數、系統失效階數、零件的性能和工作載荷是影響系統相關失效的主要因素，結合工程實際獲得的相關失效信息，本文通過系統零件個數、系統失效階數、系統低階失效數據和統計次數4個參數構建了預測系統失效概率的神經網絡參數化模型。K/N系統BP神經網絡模型輸入和輸出層節點設置見表1。

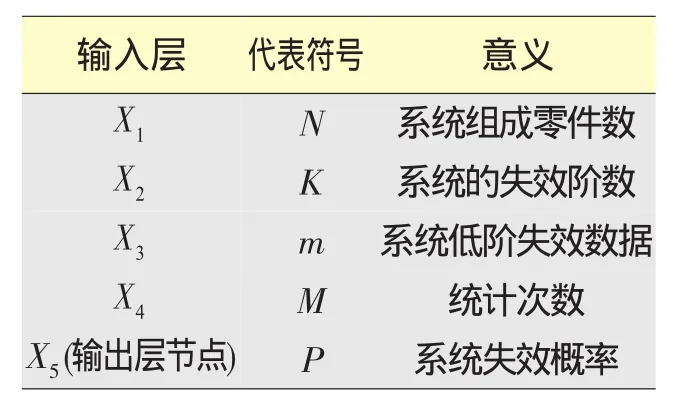
表1 K/N系統BP網絡模型輸入和輸出層節點設置

（3）網絡模型的訓練。按照上述參數訓練網絡，在得到的樣本集中取m個樣本作為訓練集，nm個樣本作為測試集。反復地應用訓練集樣本訓練網絡，使得誤差信號最小，最后使得信號誤差在允許的范圍之內，就結束網絡訓練過程。下一步是進行測試，測試集的準備是必須的，它可讓用戶了解神經網絡對未知點的推廣能力，即泛化能力。如果泛化能力太差，自然不能得到準確的系統可靠性結果。通過測試后，就可以得到系統失效概率的神經網絡模型。

綜上所述，基于神經網絡的冗余系統參數化模型，通過蒙特卡羅模擬產生的實驗數據作為神經網絡的訓練樣本，在BP神經網絡模型中進行訓練，直到建立正確的神經網絡模型。該模型可以在系統失效數據發生改變的情況下，輸入新的失效數據，輸出相應的任意階失效概率。

5 實例計算

該實例是對由10個閥組成的冗余系統（10階冗余系統）在34次需求中發生的失效事件數據進行系統失效概率預測[9]。失效事件包括具有不同失效階次的閥門“不能正常開通”失效事件，其中包括5次單個零件失效，2次2重失效，1次3重失效，還有26次成功事件。該例表明，在對零件的340(34×10)次需求中，共有12(5×1+2×2+1×3)個零件失效（見表2）。顯然，這些數據中既包含零件的失效概率信息，也包含系統相關失效信息。當估算零件失效概率時，單個零件失效事件與多重失效事件沒有本質的區別，所有失效資料可以混合使用。因此，估算的零件失效概率為12/340=0.035（每次需求），這是在概率風險分析中常用的方法。

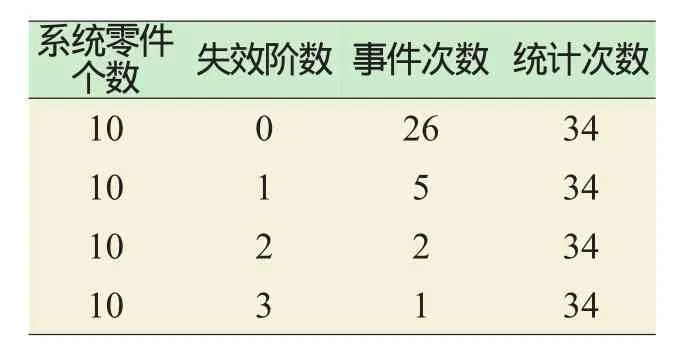
表2 10階冗余系統的共因失效數據

5.1 訓練樣本的構成

神經網絡的網絡訓練需要大量的學習樣本。本文使用蒙特卡羅的方法模擬不同冗余系統的可靠性數據訓練網絡。通過更改系統的零件個數、應力、強度等參數就可以得到不同K/N系統的失效數據，獲得神經網絡的學習樣本數據(見表3)。

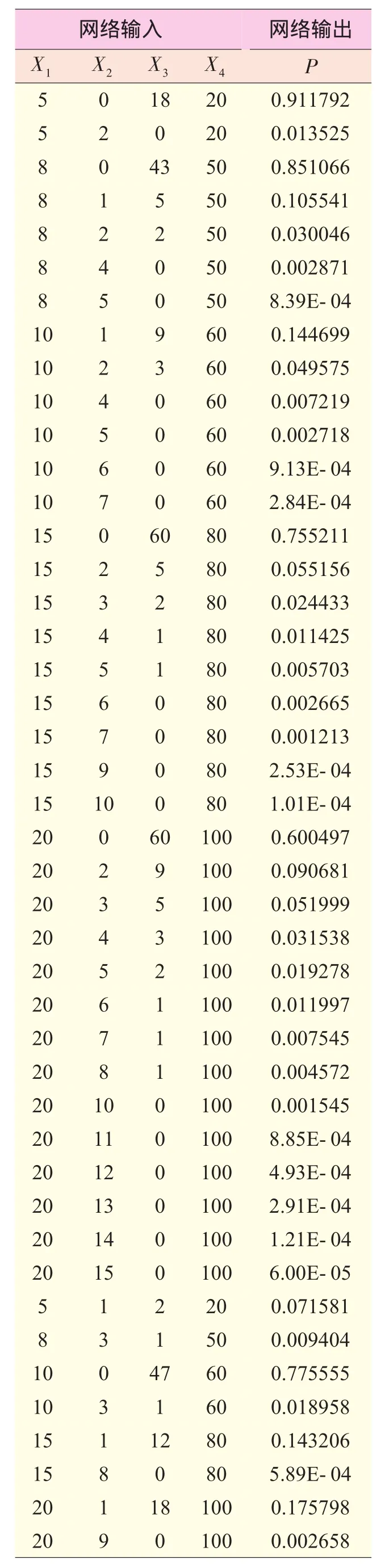
表3 K/N系統神經網絡模型學習樣本

5.2 訓練網絡

將獲得的44組數據分為2部分，前36組數據為神經網絡的訓練樣本集，剩下的8組數據為驗證樣本集。

由于中間隱含層的選取目前尚無理論指導，必須通過試算憑經驗選取。憑經驗做法，通過試算，選取1層中間隱含層的BP模型，網絡的節點層數為4-16-1，網絡模型如圖3所示，即網絡模型為1個3層BP模型，包括輸入層、1層中間隱含層和輸出層。輸入層有4個節點，分別對應系統零件個數、系統失效階數、系統低階失效數據和統計次數4個參數，即X1、X2、X3、X4；輸出層只有1個節點，對應于系統的失效概率P，傳輸函數為Tan-Sigmoid函數。該網絡能夠給出很好的計算結果。

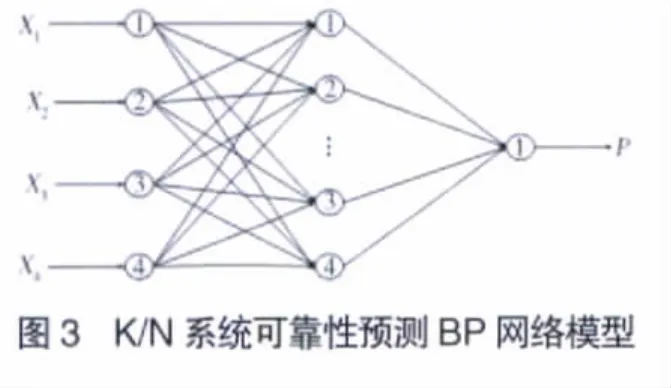
在網絡訓練時，先將輸入/輸出模式集進行歸一化[10]之后，再送入網絡進行學習，并隨機為網絡連接權值和閾值賦[-1,1]的值。取學習率α=0.03，控制精度E=0.000001，訓練次數為5000次，網絡經過多次學習之后達到收斂精度要求，應用trainlm方法訓練網絡的誤差變化曲線如圖4所示。

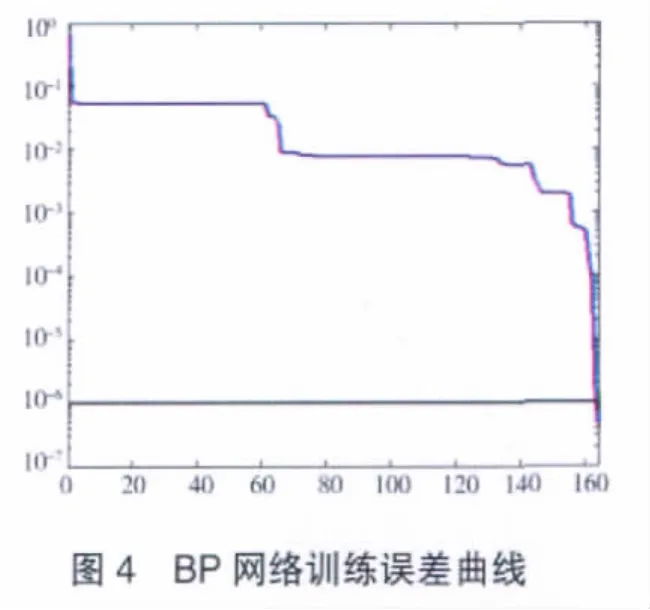
將訓練好的神經網絡進行測試，最大相對誤差小于4.5%，測試結果見表4。由分析結果可知，用神經網絡模型來分析其系統可靠性，其分析精度能夠滿足工程要求。

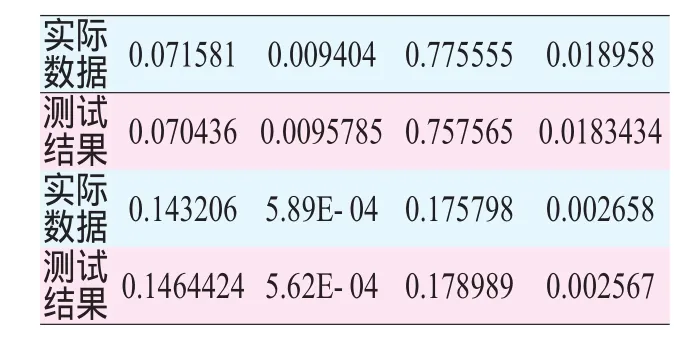
表4 BP網絡模型的測試結果

5.3 可靠性計算

當輸入條件改變時，不同結構的冗余系統又要重新進行可靠性評估。如系統的零件個數發生了變化，不同失效階數時，不同的失效數據條件下獲得的系統的失效概率是完全不同的，在這種情況下，可以應用創建的神經網絡基于新的輸入數據對系統進行可靠性分析。

將新的失效數據及其系統組成作為神經網絡的輸入向量，輸入神經網絡，運算后得到1個輸出向量，即系統的各階失效概率。

對于該實例的冗余系統失效概率的預測問題，根據表2中的失效數據，輸入上面建立好的神經網絡模型得出計算結果，系統的各階失效概率如圖5所示。

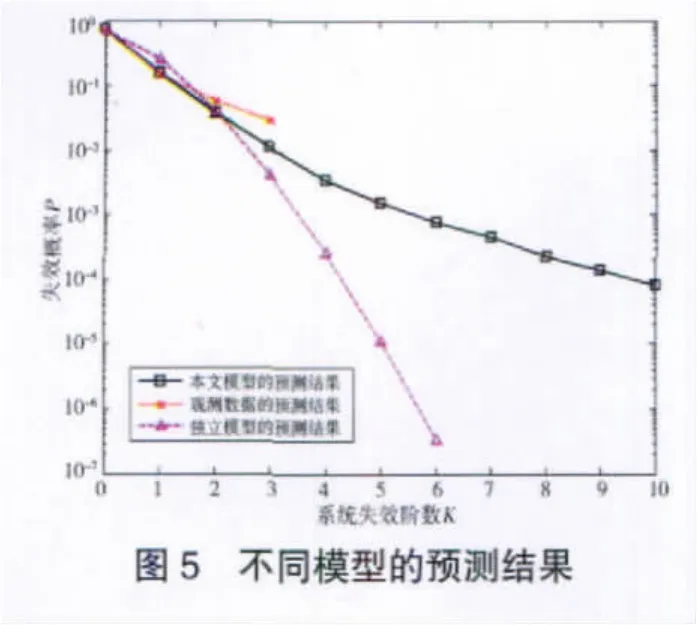
圖5示出了根據前述神經網絡模型估算的各階失效概率與應用傳統的獨立失效模型估算的失效概率及觀測值的比較。從圖中可見，與直接觀測的數據相比較，這個網絡模型得出了與觀測值較為接近的結果。但獨立失效模型對前面2階失效概率的估算也與觀測值一致，但到3階失效時，其估算結果明顯偏離了觀測結果。這種誤差趨勢反映了失效階次越高，共因失效對系統可靠性的影響就越大，獨立失效的計算結果誤差就越大。冗余系統可靠性的網絡模型是以可靠性失效數據為基礎，在得到較低階實驗數據驗證的前提下，能對較高階的共因失效概率做出同樣精確的預測，有較強的普適性。

6 結束語

系統相關失效同零件失效之間有著復雜的非線性關系。本文運用人工神經網絡的方法，建立基于BP網絡的考慮系統相關失效的冗余系統的可靠性預測的參數化模型。不依賴于任何模型假設，只需要低階失效數據就可以得到系統的高階失效概率，建立了系統失效概率與零件失效數據的非線性關系，避免了由模型假設所帶來的不確定性。利用該模型可以預測系統中的任意階相關失效概率。從建模過程及算例結果來看，該方法具有較好的非線性函數的擬合能力和推廣能力，為今后可靠性工程進行系統失效概率預測提供了新的方法，具有一定的工程應用價值。

[1] Fleming K N,Mosleh A,Deremer R K.A Systematic Procedure for the Incorporation of Common Cause Events into Risk and Reliability Models[J].Nuclear Engineering and Design(S0029-5493),1986,93:245-273.

[2] 謝里陽，王正，周金宇，等.機械系統可靠性基本理論與方法[M]北京：科學出版社，2009.

[3] 樓順天，施陽.基于MATLAB的系統分析與設計—神經網絡[M].西安：西安電子科技大學出版社，2000.

[4] 尹曉偉，錢文學，謝里陽.基于人工神經網絡的復雜機械結構安全性分析[J].機械與電子，2008(1):3-6.

[5] 巫影，陳定方，唐小兵，等.神經網絡綜述[J].科技進步與對策，2002，6(19):133-134.

[6] 飛思科技產品研發中心編著.神經網絡理論與MATLAB7實現[M].北京：電子工業出版社，2005.

[7] 薛定宇，陳陽泉.高等應用數學問題的MATLAB求解[M].北京：清華大學出版社，2004.

[8] 肖剛，李天柁.系統可靠性分析中的蒙特卡羅方法[M].北京：科學出版社，2003.

[9] Liyang Xie.A Knowledge-based Multi-Dimension Discrete Common Cause Failure Model[J].Nuclear Engineering and Design(S0029-5493),1998,183:107-111.

[10] 叢爽.面向MATLAB工具箱的神經網絡理論與應用[M].合肥：中國科技大學出版社，1999.