航空發動機使用可靠性研究

陳卓，薛慶增，李冬，崔倩

(1.海軍航空工程學院研究生管理大隊，山東煙臺，264001;2.中國人民解放軍92076部隊，北京，102202；3.海軍駐沈陽導彈專業軍事代表室，沈陽110043；4.海軍飛行學院教研部，遼寧葫蘆島，125001）

1 引言

航空發動機性能的優劣直接影響飛機性能的好壞。在使用過程中，有關人員積累了一定數量的發動機故障數據和維修數據，但對發動機可靠性水平和綜合保障效能沒有系統評估，缺乏對可靠性數據的深層次了解；維修模式、保障模式仍是根據生產方和使用經驗制定的，在某些方面還存在著不符之處；特別是在備件供應方面，盡管已經實現了部分產品國產化，具備了一定的本地修理能力，但關鍵部件制造和維修還依賴國外。

本文基于發動機使用過程中的故障數據,對發動機使用可靠性和備件需求量進行分析；利用改進后的故障數據對發動機在使用階段的可靠性增長情況進行分析。

2 可靠性數據分析

進行模型參數估計主要有2種方法：圖形法和解析法。以圖形法估計模型參數依據的是在特定概率紙上畫出的數據圖形；解析法有多種，如矩法、最小二乘法、極大似然法。

在發動機附件可靠性分析中，對2參數威布爾分布方法應用較多。本文采用最小二乘法計算2參數威布爾分布，并與指數分布和正態分布擬合方法進行對比，從中找出最適合可靠性數據分布的規律。

威布爾分布[1-3]的不可靠度函數為

式中:β＞0,為形狀參數；α＞0,為尺度參數。

指數函數[4]分布的不可靠度函數為

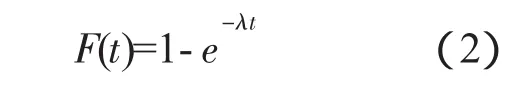
式中:t≥0；λ＞0,λ為常數。

正態分布的不可靠度函數為

式中:μ為位置參數;σ(σ＞0),為標準差。

當μ＞0，μ/σ＞3時，正態分布作為失效模型沒有太大問題;如果μ/σ＜3，模型必須經過修改，才能用于失效數據建模。

所采集的發動機某部件在使用過程中的1組故障數據見表1。

表1 發動機某部件故障數據h

在3種函數數據擬合中，均采用最小二乘法求其系數。在此基礎上，對曲線進行擬合。計算得到指數分布、正態分布和威布爾分布故障數據的回歸系數，見表2。3種函數分布故障數據的擬合效果如圖1所示。

表2 不同分布的相關系數

進一步得到的擬合的威布爾分布曲線為

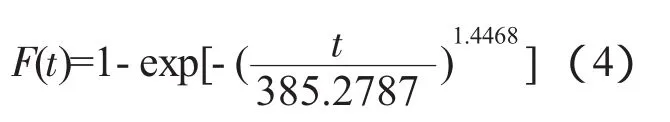
指數分布曲線為

正態分布曲線為

由圖1和表2可知，威布爾分布和指數分布擬合效果較好，威布爾分布的略好于指數分布的；正態分布的最差。原因在于這組失效數據并不服從正態分布，而且μ/σ=1.9540＜3，模型必須經過修改，才能用于失效數據建模。假定自然對數Y=ln X服從正態分布，經過計算發現，這組數據根本不服從對數正態分布。

3 基于保障率的備件需求優化

在實際情況下，航材備件還受到很多因素的影響，既受備件耗損性的影響，又受到在裝備中的重要程度—關鍵性的影響，另外還要考慮經濟性。所謂零部件的關鍵性是指該件在裝備系統中所起的作用以及對系統性能的影響程度。零部件的耗損性是指耗損程度的高低，主要與零部件的固有可靠性、使用環境及條件因素有關。這些因素有的不易量化，且與備件品種的關系是模糊的，因此，對權重的分析適合采用模糊綜合評判的方法。

在計算過程中，主要考慮部件的故障率、維修性、部件在發動機中的重要性和可得性4個方面的影響，在權值計算基礎上得出該部件的權重分數。計算過程如下。

（1）構造判斷矩陣。層次分析結構如圖2所示。

判斷矩陣是層次分析法的基本信息，判斷矩陣A中的元素aij表示從判斷準則角度考慮的元素i對元素j的相對重要性，且滿足

判斷尺度采用薩蒂9級標度，規定用1、3、5、7、9分別表示元素i對元素j同樣、比較重要、重要、很重要、極重要。構造模糊判斷矩陣A(k)。對專家評價，用模糊三角數表示模糊判斷，模糊數等級采用3級標度。專家在對重要度進行的主觀判斷有一定的置信度δ，當置信度分別為“很有把握”、“把握一般”時，δ分別取值0.5、1.0、1.5。A(k)=(aij)n×n表述為

aij為模糊判斷矩陣中的元素，因此判斷矩陣A(k)為正互反矩陣。

（2）計算歸一化權重向量。

計算第k專家確定的權重

式中：x-、x+為矩陣A-、A+最大特征值所對應的歸一化特征向量；α、β的取值為

對計算得到的權重向量w(k)進行歸一化處理，得到歸一化權重向量w0(k)。為了保證決策的可靠性，必須對模糊判斷矩陣進行一致性檢驗。采用λmax與n之差法進行一致性檢驗，即

若C.I.≤0.1，證明判斷矩陣是一致的。

（3）計算決策權重。

為了降低決策風險，評估過程有多個專家共同參與，而每個專家的主觀判斷可信度不同，設每個專家的自身權重為yk，權重為，可得決策權重

（4）確定部件的最終權重。

對每個部件的故障率、可修性、裝機重要性和可得性分別打分，對這4項的分數進行求和，得出該部件的權重分數；對權值的計算采用模糊層次分析法[5,6]，得出該部件的權重分數，然后再對所有部件的權重分數ri進行求和，得到1個總權重分數則部件的最終權重為

在上面計算步驟的基礎上，本文主要考慮故障率、可修性、重要性和可得性4個方面的影響，進行重要性評估。設專家1、2對兩兩指標重要性做出的主觀判斷和對此判斷的置信度，具體見表3。

表3 重要性比較

根據表3中信息建立判斷矩陣，并根據式（7）和式（8）將判斷矩陣轉化成定量評價矩陣

經統計得知，可更換部件中發生故障的部件主要有12個，以序號標記。各部件的故障率經大量統計得到。根據備件的故障率、可修性、重要性和可得性，并且參考相關經驗數據[7]，得到故障率、可修性、重要性、可得性在權重中分別所占的分值A、B、C、D。表4列出了備件的各項權重和相應項。

以46臺發動機為單位，按年飛行計劃200 h，要求某臺發動機LRU部件在發生故障時可以及時獲得備件的保障率在90%的最低備件數量，同時要求單個部件的保障率不低于85%，采用基于保障率的后續備件保障模型，建立最小數量要求的目標函數和約束函數。

表4 主要可更換部件權重

目標函數

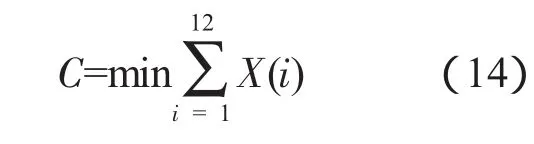
約束函數

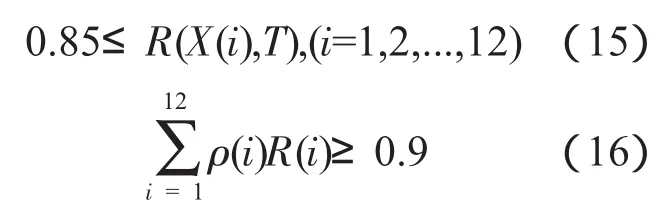
式（15）表明單個備件的保障率在85%以上；式（16）表示單臺發動機LRU部件在發生故障時，能夠及時得到備件的保障率在90%以上；在式（17）中，J為（1,...,N）中的任一數值，表示當第J個備件缺1個時，系統總保障率R＜0.9；在式（18）中，X(i)為備件數量，N(i)為第i個部件的裝機數量，t為第λi個部件的失效率，t為年飛行時間。

在Matlab7.0仿真環境中，利用最優化工具箱中提供的fmincon函數求解，得到2種情況（基于備件數量最優，基于備件費用最優）各部件所需數量和費用。計算數據均取整數值，結果見表5、6。

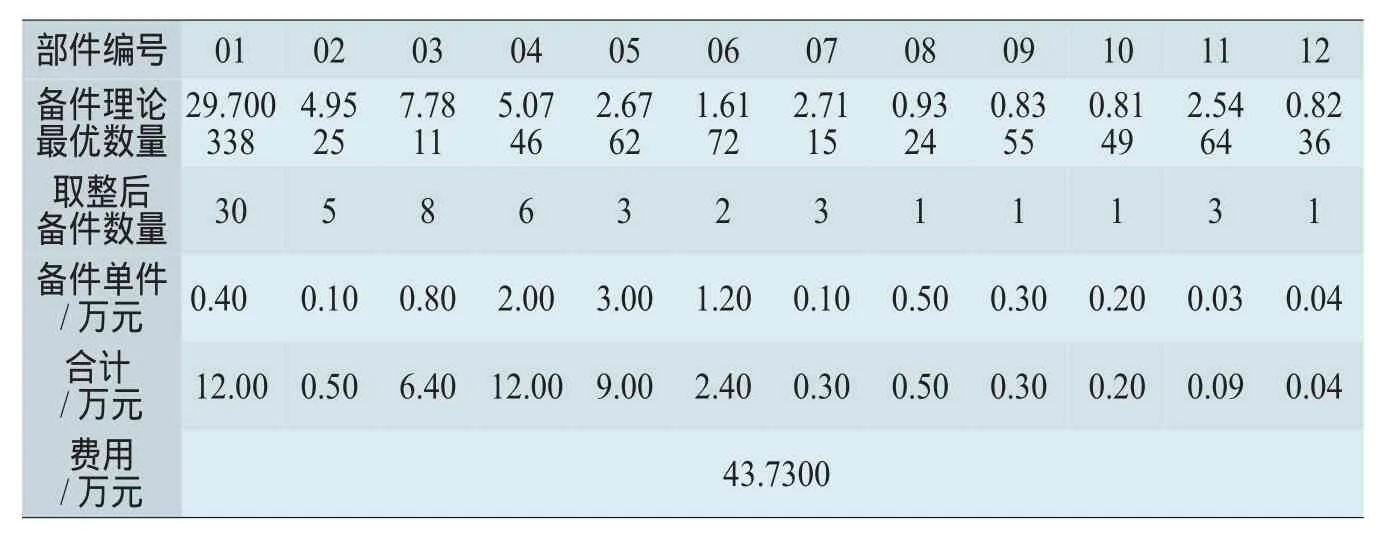
表5 最優備件數量

表6 最優備件費用

以上計算得到的最優備件數量，目標函數是基于最小備件數量得到的。下面將目標函數改為基于最小費用的函數，約束函數不變，得到的最優備件費用和相應的備件數量見表6。

目標函數

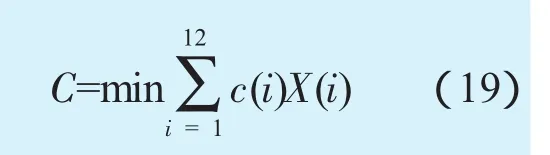
式中：c(i)為單個備件價格，X(i)為相應的備件數量。

4 可靠性增長分析

發動機工作可靠性評定的過程，也是發動機可靠性成熟和增長的過程。利用收集到的部件故障數據，對發動機部件可靠性增長情況進行分析。采用AMSAA模型[8]進行分析，假設可修產品在開發期(0,t]內的失效次數N(t)是具有均值函數EN(t)=v(t)=atb及瞬時強度λ(t)=abtb-1的非齊次poisson過程｛N(t);t≥0｝，也稱為冪律過程。

可修產品開發到時刻T后，不再進行設計改進和糾正。此際，可以認為產品定型后，其故障分布服從指數分布，即

定型時的MTBF稱為產品能達到的MTBF，即

4.1 可靠性增長趨勢分析步驟

可靠性增長趨勢[9，10]分析的主要步驟如下。

（1）將觀察到的累計試驗時間ti從小到大依次排列，按下式計算試驗趨勢統計量μ

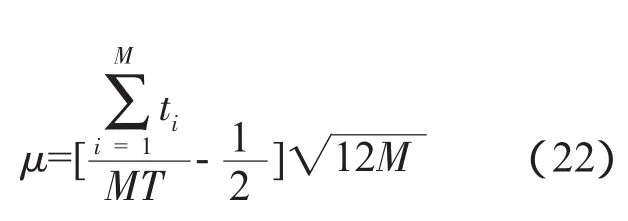
式中：T為試驗累計總時間；N為觀察到的故障總數；M的取值為N。

（2）根據給定的顯著性水平α，從表中查得μ0值，其中μ0=μ1-α/2。

（3）試驗趨勢分為3種情況：

a.當μ＜-μ0時，以顯著性水平α表示有明顯的可靠性增長趨勢；

b.當μ＞-μ0時，以顯著性水平α表示有明顯的可靠性降低趨勢；

c.當-μ0＜μ＜-μ0時，以顯著性水平α表示沒有明顯的可靠性變化趨勢。

4.2 參數估計

本文利用在時間截尾情況下的2種估計方法，進行參數估計。對增長參數和的估計式，采用極大似然估計與近似無偏估計2種方法。

采用極大似然估計方法

采用近似無偏估計方法

式中:T為時間截尾的總時間;ti為第i次故障的發生時間;n為累積故障數。

4.3 擬合優度檢驗

試驗數據是否符合AMSAA模型，需要進行擬合優度檢驗。其方法是利用排序的試驗數據t1＜t2＜...＜tn，按下式計算和擬合優度檢驗統計量

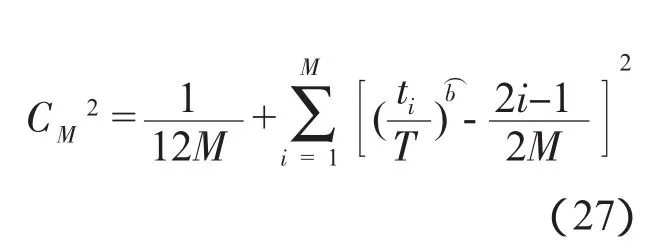
然后，根據選定的顯著性水平α，從克萊默-馮梅賽斯檢驗表中查出與M及α相應的檢驗臨界值如果＜，則接受AMSAA模型，反之，則拒絕AMSAA模型。

4.4 計算實例

本文利用收集到的維修改進后的故障數據，對整機的使用可靠性增長進行驗證。采用AMSAA模型，在1000 h截尾，共出現20次故障；故障記錄及中間計算結果見表7。

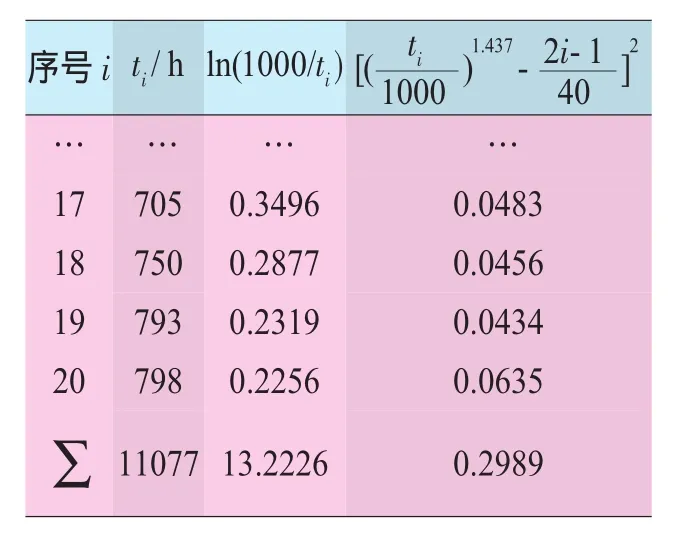
表7 故障記錄及中間計算

采用AMSAA模型，對其進行如下的可靠性增長分析。

（1）增長趨勢檢驗。

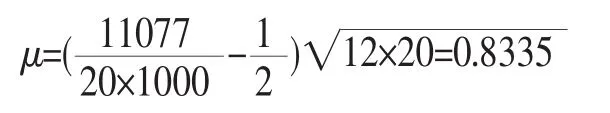
查α=10%的臨界表，得μ0=1.645；由于μ=0.8335＜1.645=μ0，該組數據表明的可靠性有明顯增長趨勢。

（2）參數估計。

采用極大似然估計方法

采用近似無偏估計方法

由以上的分析結果可以判斷出，對單個部件進行的維護改進和維護規程的完善增強了發動機使用可靠性，從而可以判斷出部件改進和維護規程完善是正確、合理的。

5 結論

本文基于航空發動機使用可靠性數據，對試驗數據進行擬合分析。驗證發現，試驗數據服從威布爾分布，且威布爾擬合精度高于指數分布和正態分布2種方法的；隨使用維護時間的增加和各種維護措施的不斷完善，部件使用可靠性逐漸增強。

[1] 張慧敏.三參數威布爾分布在機械可靠性分析中的應用[J].機械管理開發，2009，24(3)：59-60.

[2] 方志強,高連華.三參數威布爾分布在壽命分析中的參數估計[J].裝甲兵工程學院學報，1999(3):12-15.

[3] 刁柏青,蔣昌俊.確定威布爾分布三參數的一種計算方法[J].山東礦業學院學報，1993，(3):285-288.

[4] 李湘寧,張艷.指數型數據環境因子工程計算方法[J].火力與指揮控制,2009(34):164-166.

[5] 崔南方,羅雪.維修備件基于AHP的ABC分類模型[J].工業工程與管理,2004(6):33-36.

[6] 馬利,陳東林.模糊綜合評判理論在備件供應保障中的應用[J].航空計算技術，2004，34(2):19-24.

[7] 孫旭波.某型航空發動機使用可靠性分析與應用[M].山東煙臺:海軍航空工程學院,2010.

[8] 周源泉,劉振德.某型渦扇發動機的可靠性增長分析與評估[J].質量與可靠性，2004(3)：42-45.

[9] 陳紹憲.AMSAA模型的增長分析[J].電子產品可靠性與環境試驗,2001(1):66-72.

[10] MIL-HDBK-189.Reliability growth managment[S].1981.