脈沖爆震火箭發動機噴管構型數值研究

李建玲，范瑋，李強，嚴傳俊

（西北工業大學動力與能源學院，西安710072）

1 引言

脈沖爆震火箭發動機[1,2](Pulsed Detonation Rocket Engine,簡稱PDRE)是1種利用周期性爆震波發出的沖量產生推力的非穩態新型推進系統。由于PDRE具有熱效率高、結構簡單、尺寸小、質量輕、工作范圍廣等諸多潛在優勢，目前世界很多國家都對PDRE開展了研究。排氣噴管是PDRE的重要部件之一，對于提高PDRE的推進性能起著非常重要的作用。對于常規液體火箭發動機等以穩態方式運行的噴氣發動機而言，排氣噴管技術已經比較成熟。但是，PDRE的非穩態運行特點對排氣噴管的設計、選取和分析研究帶來了挑戰性難題，至今還沒有發展出能夠指導PDRE排氣噴管設計的理論[3]。由于噴管構型、推進劑、初始條件等研究條件存在差異，對于噴管效用的研究結論也不盡相同，甚至出現一些相互矛盾的情況[4]。

本文采用準1維數值模型，研究了噴管構型對PDRE單次爆震過程流動以及排氣性能的影響。

2 控制方程和計算方法

這里首先指出，PDRE零維模型是經典的熱力循環分析模型，可以反映出爆震室內的初始壓力、初始溫度以及混合物當量比等主要影響因素對其性能的影響，雖然計算量小，但無法考慮波的相互作用以及非穩態流動過程對PDRE性能的影響；采用多維模型估算出的PDRE性能更可靠，但計算量顯著增加。而本文所采用的準1維模型，則考慮了PDRE大部分的實際工作過程，計算量適中，可用于快速評估PDRE的推進性能，為PDRE排氣噴管選擇提供參考。

采用單進程變量化學反應模型，忽略氣體黏性、導熱以及擴散運動，描述爆震燃燒化學反應過程的準1維Euler方程為

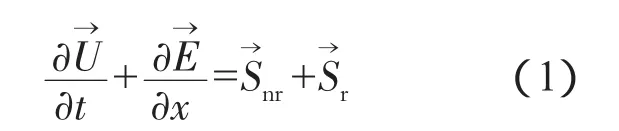
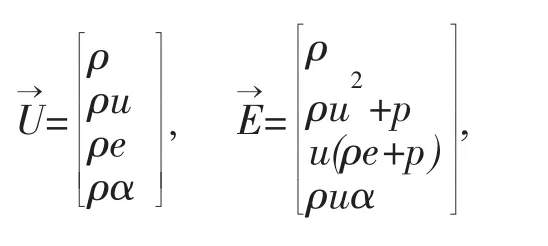
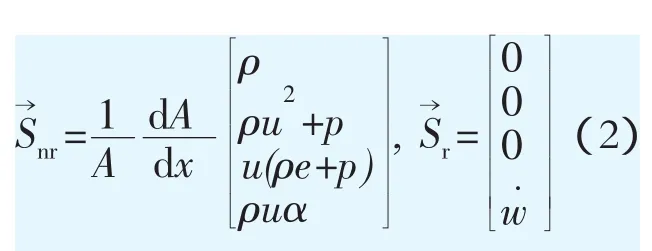
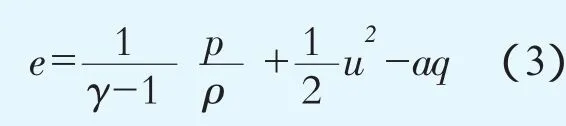
式中：γ為比熱比；q為單位質量反應物放熱量；w˙為反應產物的質量生成速率，用Arrhenius形式表示為

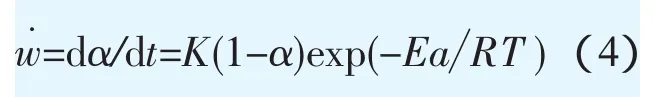
式中：K、Ea、R、T分別為化學反應的指前因子、單位質量反應物的活化能、氣體常數和溫度。溫度T由理想氣體狀態方程給出

對于化學反應流計算，尤其是爆震問題，化學反應的特征時間（通常微秒量級）往往比流動特征時間小幾個數量級。這使得控制方程具有了強剛性，給數值求解控制方程組帶來困難。利用2階精度Strang算子分裂法[5]來分離剛性源項，將原來的控制方程組（式（1））分裂成2個方程組：1個描述流場的齊次偏微分方程組（含非剛性源項）和另1個描述化學反應的常微分方程，對每個方程組采用不同方法進行積分求解。采用AUSM格式[6,7]進行空間離散，將無黏通量分裂為對流通量項及壓力通量項來處理。時間離散采用3階TVD龍格－庫塔格式[8]。采用多步隱式方法離散含剛性化學源項的常微分方程，對所得到的非線性方程利用Newton-Raphson迭代方法求解。

此外，在控制方程中，涉及到與化學熱力學和化學動力學相關的5個參數（γ，R，q，Ea，K）。對于化學恰當比的氫氧混合物（2H2+O2），這5個參數參照文獻[9]、[10]給出。

3 物理模型和邊界條件

本文研究的4種PDRE構型均為1端封閉、1端敞口。選作基準構型的理想PDRE為不帶噴管的均勻直管，爆震管內徑為40 mm，長度為200 mm。3種帶噴管的PDRE構型如圖1所示，爆震管內徑為40 mm，長度為200 mm，噴管長度均為30 mm。在圖1（a）中，收斂噴管出口直徑為32 mm，噴管面積比為0.8；在圖1(b)中，擴張噴管出口直徑為50 mm，噴管面積比為1.25；在圖1（c）中，收斂擴張噴管喉部直徑為32 mm，噴管收斂段和擴張段角度分別為45°和15°。

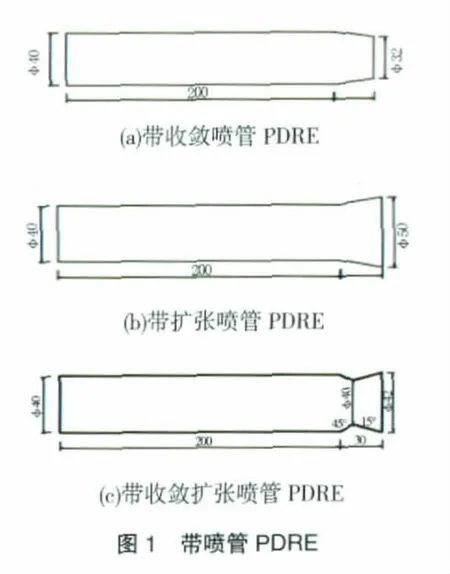
在初始時刻，爆震管內完全填充靜止的化學恰當比的氫氧混合物，噴管內填充靜止的不可爆物質。由靠近封閉端的高溫高壓區直接起爆。高溫高壓點火區寬度為1 mm，壓力和溫度分別為200 kPa和3000 K。其它區域的初始壓力和溫度分別為100 kPa和293 K。爆震管左端推力壁為無黏絕熱固體壁面。出口邊界條件由出口流動情況確定，當出口流動為超聲速和聲速時，采用超聲速出口邊界；當出口流動為亞聲速時，采用亞聲速出口邊界。環境壓力和溫度分別為100 kPa和293 K。

4 流場特性和性能分析

4.1 基準構型PDRE計算結果

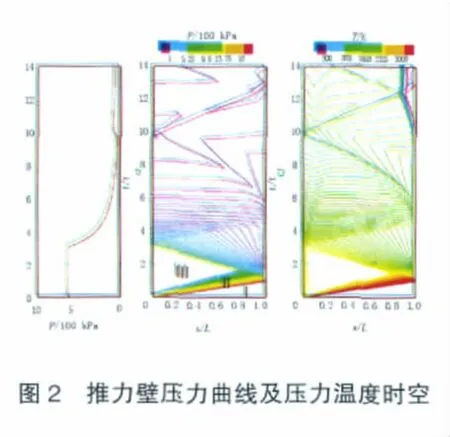
基準構型PDRE單次爆震過程的推力壁壓力曲線及壓力溫度時空如圖2所示，其中壓力溫度時空圖的橫、縱坐標分別被無量綱化。L表示爆震管長度（200 mm），tCJ等于爆震管長度除以CJ爆震波速。在圖2中，Ⅰ區為爆震波前未受擾動的可爆混合物，Ⅱ區為Taylor膨脹波區，Ⅲ區為Taylor膨脹波波尾與推力壁之間的均勻區。爆震波以恒定速度向敞口端傳播。從0時刻到爆震波到達敞口端的時間（爆震波傳播時間）為0.0715 ms。爆震波到達爆震管敞口端后，在外界空氣中形成透射激波，同時產生向爆震管內傳播的反射特征膨脹波。反射特征膨脹波與Taylor膨脹波相互作用形成非簡單區。可見，在排氣過程中，流動受到多種波影響，流動情況比較復雜。

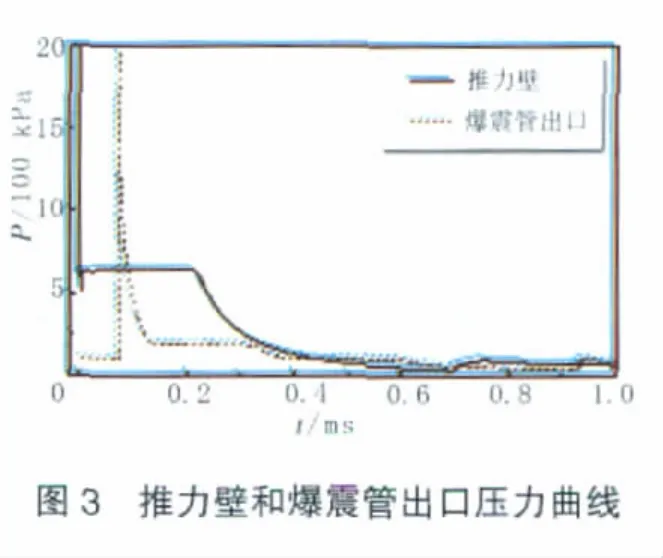
在單次爆震過程中，爆震管推力壁和出口壓力曲線如圖3所示。從爆震波形成直到第1道反射特征波到達封閉端前，封閉端的壓力一直維持1個均勻值不變，呈現為推力壁壓力平臺區。隨著第1道反射特征膨脹波的到達，更多的反射特征膨脹波到達封閉端，推力壁壓力開始逐漸減小；,在壓力減小過程中，會出現短時間的過度膨脹，推力壁壓力略低于外界環境壓力。隨著排氣過程的進一步進行，推力壁壓力最終趨同于外界環境壓力。爆震波達到爆震管敞口端前，爆震管出口壓力等于可爆混合物初始填充壓力；當爆震波到達敞口端，出口壓力迅速增大；隨著爆震波和爆震波后高壓氣體的逐漸排出，出口壓力迅速減小。此外，在單次爆震排氣過程中，雖然推力壁壓力的壓力已經減小至接近外界環境壓力的水平，但是推力壁處的溫度仍然較高，整個爆震管內的氣體溫度也較高。

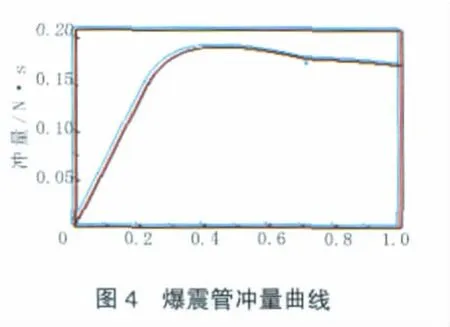
基準構型PDRE的沖量隨時間變化曲線如圖4所示。從0時刻（點火時刻）開始，爆震管推力壁壓力高于外界環境壓力，并產生推力，PDRE所產生的沖量逐漸增大。隨著排氣過程的不斷進行，推力壁壓力逐漸減小，沖量增大趨勢變得較為平緩。當推力壁附近出現過度膨脹時，推力壁壓力開始略低于外界環境壓力，PDRE產生的瞬時推力為負，沖量略微減小。在0.4463 ms時刻，PDRE產生的沖量達到最大值0.19223 N·s。在1 ms內，基準構型PDRE的沖量及以可爆混合物為基礎的質量比沖分別為0.172101 N·s和130.436 s。在相同的可爆混合物以及相同的初始條件下，采用熱力學循環分析和性能計算[11]得到的理想爆震循環比沖為182.63 s。因此,基準構型PDRE單次爆震過程的質量比沖低于熱力學計算值，這主要是由于爆震波后的高溫高壓燃氣的內能并未完全轉化為排氣動能產生的推力。可以考慮在爆震管后安裝排氣噴管，來充分利用高溫高壓燃氣的內能，以提高PDRE推進性能。

計算PDRE沖量（推力）的方法一般有進、出口平面動量平衡法和壁面壓力積分法[11]。進、出口平面動量平衡法是取整個PDRE內的流體為控制體，根據動量守恒推導出PDRE瞬時推力的計算公式。對于單次爆震排氣過程，如果利用爆震管出口流動來確定排氣過程所產生的沖量，計算時間必須足夠長，才能夠消除非穩態效應的影響。因此,采用壁面壓力積分法來計算PDRE瞬時推力。對于均勻直管構型的PDRE，可以通過推力壁壓力積分得到其沖量。但對于非均勻直管構型的PDRE（如直爆震管后帶有非等截面直管構型的排氣噴管），推力壁壓力積分結果不能反映整個發動機的推進性能，而需要對發動機所有固體壁面進行積分。

4.2 收斂噴管PDRE計算結果

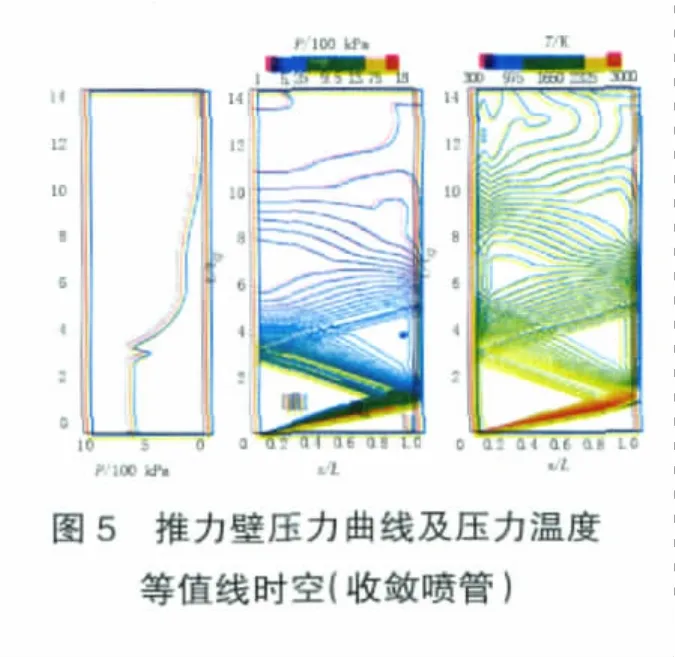
帶收斂噴管PDRE單次爆震過程的推力壁壓力曲線及壓力溫度時空如圖5所示。在爆震波到達噴管入口前，其流動情況與直爆震管的完全相同。爆震波到達可爆混合物與不可爆震物質的界面時，向爆震管上游反射膨脹波。當透射激波與噴管收斂段相互作用后，向上游反射壓縮波，但并不是所有收斂段都首先反射出壓縮波。收斂段首先反射膨脹波還是壓縮波，取決于可爆混合物與不可爆震物質的界面位置、收斂段收斂角度等因素。反射的膨脹波和壓縮波與爆震波后的Taylor膨脹波相互作用，形成更為復雜的波系。當膨脹波和壓縮波到達推力壁后，推力壁壓力有1個迅速減小并恢復的過程。隨著更多的膨脹波逐漸傳播到推力壁，推力壁壓力開始逐漸降低。帶有收斂噴管的PDRE推力壁壓力降低至環境壓力的時間約為基準構型PDRE的1.651倍。

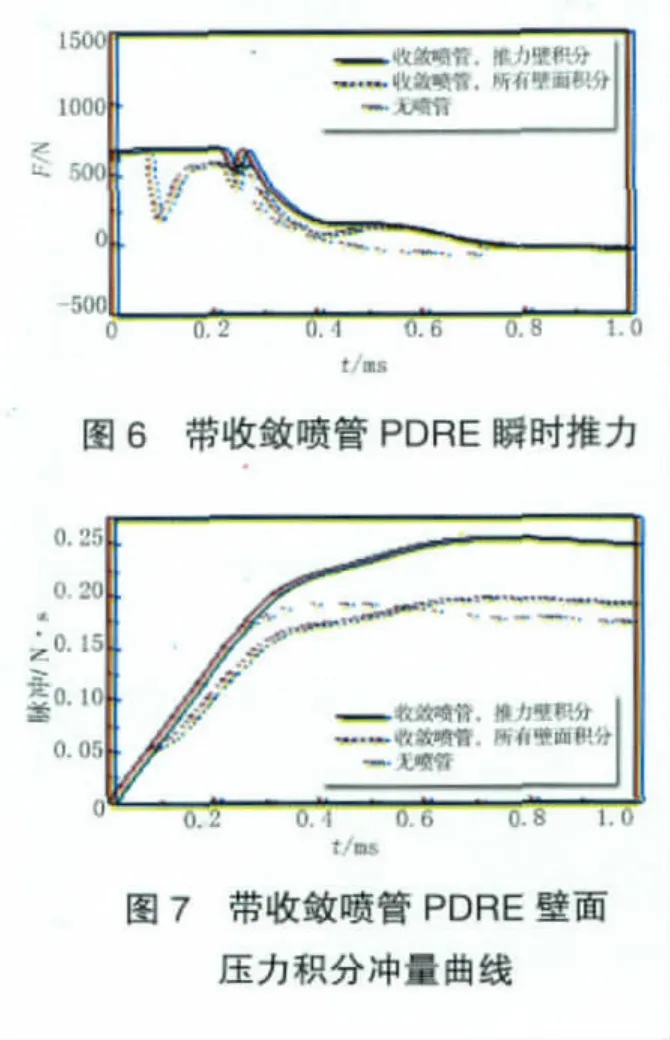
帶收斂噴管PDRE的瞬時推力和壁面壓力積分沖量曲線分別如圖6、7所示。由圖中可知，以推力壁壓力積分和所用壁面壓力積分得到的瞬時推力曲線存在較大差別。在爆震波到達噴管入口前，瞬時推力保持不變；當爆震波進入噴管，爆震波轉化為激波，高壓氣體與噴管收斂段壁面作用產生負推力，使得整個PDRE推力迅速減小，隨著氣體排出，推力逐漸增大，并維持在一定水平基本不變。期間，推力的小幅減小并回升是由推力壁壓力變化所引起的；隨著排氣過程進行，推力開始逐漸減小。在0.72665 ms時刻，帶收斂噴管PDRE沖量達到最大值0.1972 N·s；在1 ms內，PDRE的沖量和比沖分別為0.190274 N·s和144.205 s。在相同積分時間內，帶收斂噴管PDRE所產生的沖量比基準構型產生的沖量提高10.556%；但這一比沖值仍低于理想爆震循環的比沖（182.63 s），可以通過進一步優化排氣噴管來提高。

4.3 擴張噴管PDRE計算結果

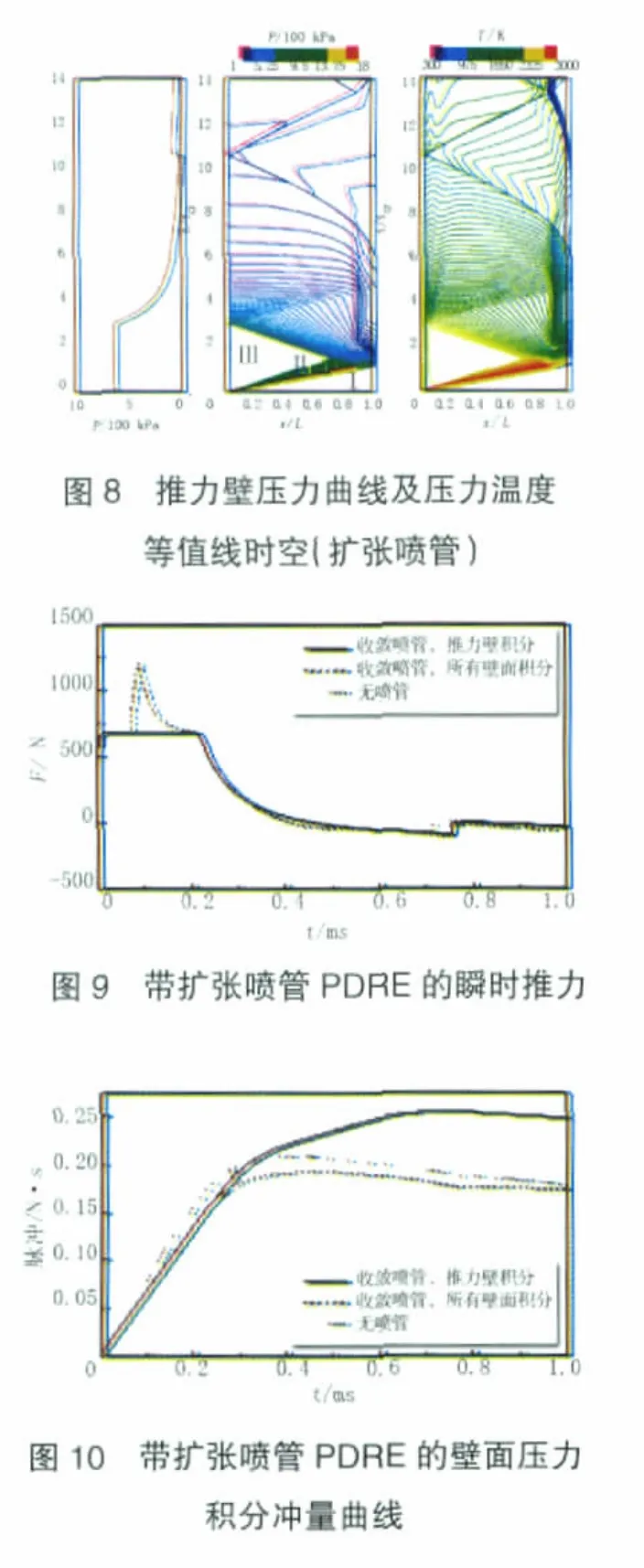
帶擴張噴管PDRE單次爆震過程的推力壁壓力曲線及壓力溫度時空如圖8所示。帶擴張噴管PDRE的推力壁壓力曲線與基準構型PDRE的推力壁壓力曲線基本相同。帶擴張噴管PDRE的瞬時推力和壁面壓力積分沖量曲線分別如圖9、10所示。爆震波進入噴管后轉化為激波，在高壓氣體與噴管擴張段壁面作用下，整個爆震管的推力迅速增大。隨著排氣過程的進行，推力逐漸減小；在排氣過程后期，擴張噴管中的氣流過度膨脹。在0.4035 ms時刻，帶擴張噴管PDRE的沖量達到最大值0.20968 N·s；在1 ms內，PDRE的沖量和比沖分別為0.177661 N·s和134.646 s，比基準構型的提高了3.227%。

4.4 收斂擴張噴管PDRE計算結果

帶收斂擴張噴管PDRE單次爆震過程的推力壁壓力曲線及壓力溫度時空圖如圖11所示。

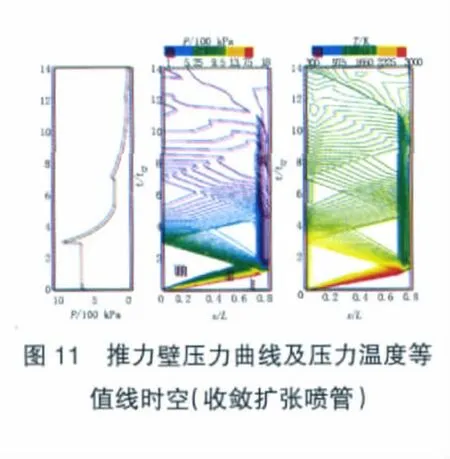
從圖中可以看出，除了存在與基準構型PDRE壓力溫度時空圖中相似的Taylor膨脹波區（Ⅱ區）和均勻區（Ⅲ區）外，收斂擴張噴管內還存在非常復雜的非定常波系（Ⅳ區）。在爆震波到達收斂擴張噴管入口前，其流動情況與不帶噴管的直爆震管流動完全相同。當爆震波與噴管收斂段相互作用后，從噴管收斂段向上游反射壓縮波；反射的壓縮波與爆震波后的Taylor膨脹波相互作用，形成更為復雜的波系；當壓縮波到達推力壁后，推力壁壓力有1個迅速增大的過程。隨著從噴管出口反射的膨脹波的逐漸傳播到推力壁，推力壁壓力開始減小，減小至環境壓力的時間約為基準構型的1.544倍。收斂擴張噴管的存在，使得帶收斂擴張噴管PDRE的排氣過程較基準構型的更為復雜。

帶收斂擴張噴管PDRE的瞬時推力和壁面壓力積分沖量曲線分別如圖12、13所示。在爆震波到達噴管入口前，瞬時推力保持不變；當爆震波進入噴管轉化為激波后，在高壓氣體與噴管收斂段壁面作用下產生負推力，使得整個發動機的瞬時推力急劇減小。隨著高壓氣體進入噴管擴張段，爆震管推力迅速增大，并維持在一定水平基本不變。PDRE的推力在呈現1個迅速增大的行程后，隨著排氣過程的繼續進行，開始逐漸減小。在0.636ms時刻，帶收斂擴張噴管PDRE的沖量達到最大值0.19334 N·s；在1 ms內，PDRE的沖量和比沖分別為0.18032N·s和136.661 s，比基準構型的提高4.772%。4種構型PDRE單次爆震的推進性能見表1。

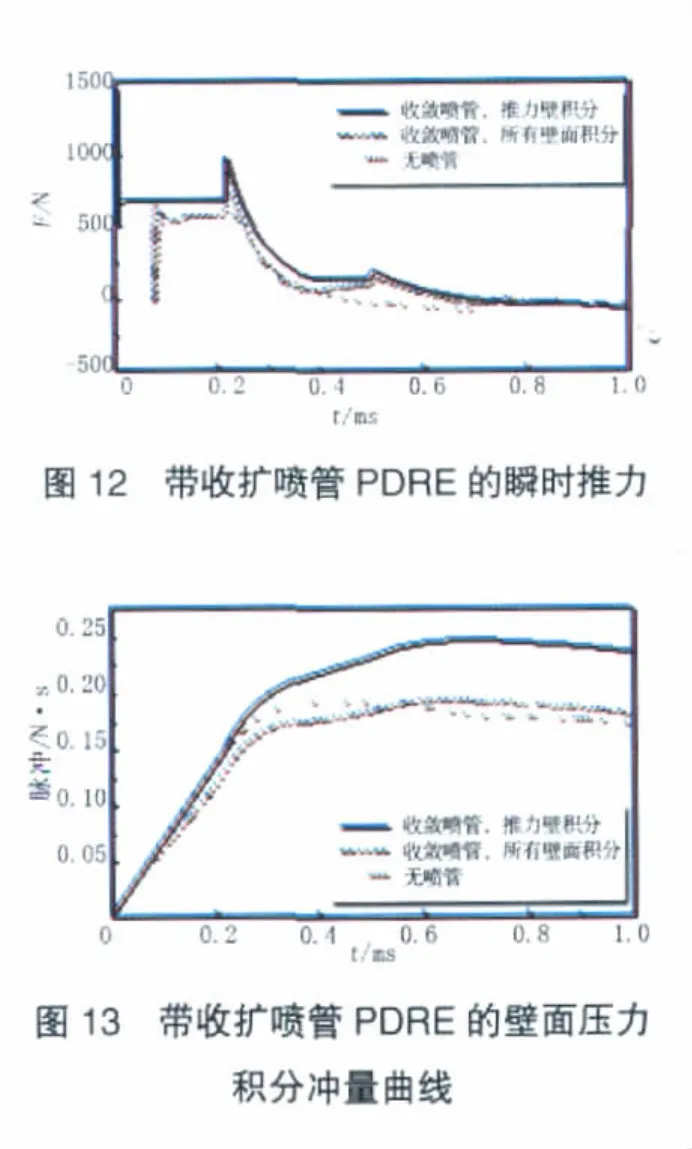
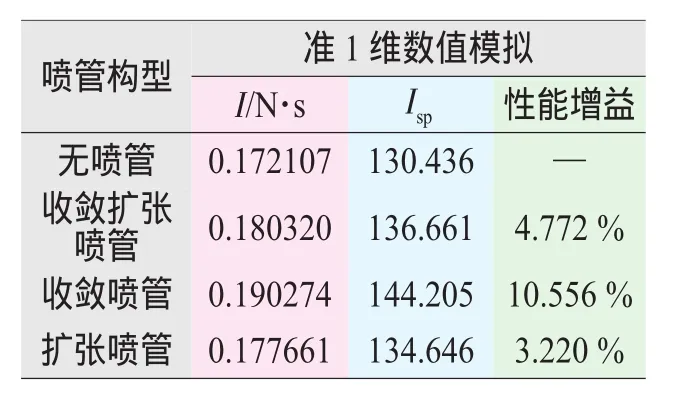
表1 4種構型PDRE推進性能比較

5 結論

通過對帶噴管和不帶噴管PDRE單次爆震排氣過程的數值仿真可知，在爆震管完全填充的條件下，各種構型的噴管都能產生性能增益。噴管收斂段的存在，使得帶收斂擴張噴管和收斂噴管PDRE的內部流場比不帶噴管PDRE和帶擴張噴管PDRE的更為復雜，推力壁壓力松弛時間更長。帶收斂噴管PDRE的性能增益最大，達到10.556%，但其值仍遠低于理想爆震循環的比沖，可以通過進一步優化排氣噴管來提高比沖。由于在排氣過程的后期，擴張段內的氣流過度膨脹會造成發動機性能損失，帶收斂擴張噴管和擴張噴管PDRE的性能增益不如帶收斂噴管的。可見,PDRE的噴管設計準則與常規穩態發動機的存在明顯差異。

[1] Bussing T,Pappas G.An Introduction to Pulse Detonation Engines[C].AIAA paper 94-0263.In 32nd Aerospace Sciences Meeting and Exhibit,Reno,NV,1994.

[2] Kailasanath K.Recent Developments in the Research on Pulse Detonation Engines[J].AIAA Journal,2003,41(2):145-159.

[3] Roy G D,Frolov S M,Borisov A A,et al.Pulse Detonation Propulsion:Challenges,Current Status,and Future Perspective[J].Progress in Energy and Combustion Science,2004,30:545-672.

[4] Kailasanath K.A Review of Research on Pulse Detonation Engine Nozzles[C].AIAA paper 2001-3932.In 37th AIAA/ASME/SAE/ASEE Joint Propulsion Conference&Exhibit,Salt Lake City,Utah,2001.

[5] Strange G.On the construction and comparison of difference schemes[J].SIAM Journal of Numerical Analysis,1968（5）:506-517.

[6] Liou M S,Steffen C J.A New Flux Splitting Scheme[J].Journal of Computational Physics,1993,107(1):23-39.

[7] Liou M S,Edwards J R.Numerical Speed of Sound and its Application to Schemes for all Speeds[C].AIAA Paper 99-3268,In 14th Computational Fluid Dynamics Conference,Norfolk,VA,1999.

[8] Shu C W,Osher S.Efficient Implementation of Essentially Non-Oscillatory Shock-Capturing[J].Journal of Computational Physics,1988,77(2):429-471.

[9] Gamezo V N,Desbordes D,Oran E S.Formation and Evolution of Two-dimensional Cellular Detonations[J].Combustion and Flame,1999,116:154-165.

[10] Gamezo V N,Desbordes D,Oran E S.Two-dimensional Reactive Flow dynamics in Cellular Detonation Waves[J].Shock Waves,1999,9(1):11-17.

[11] 嚴傳俊,范瑋.脈沖爆震發動機原理和關鍵技術[M].西安：西北工業大學出版社,2005,122-198.