基于ADRC的發電機勵磁系統控制研究

李天云 安 博 戚 為 王雪奇

（1.東北電力大學，吉林 吉林 132012；2.浙江省寧波鄞州供電局，浙江 寧波 315103）

1 引言

由于電力系統是強非線性、時變系統，而勵磁控制在維持電力系統穩定中占有重要的地位，近年來發電機的非線性勵磁控制方式的研究獲得了飛速發展，并取得了豐碩的成果[1-4]。但是各種方法也各自存在不足：模糊PID等智能控制方法計算量大、控制很難滿足實時性要求；自適應控制對有純滯后、需要前饋補償且動態過程變化緩慢的系統，可做到效果較好，但對動態過程變化迅速的系統效果欠佳，并且還存在穩定性、魯棒性問題；H∞控制、變結構控制、魯棒控制等理論尚未完全成熟，數學工具抽象、復雜，應用和推廣受到影響。尤其是在實際發電廠中存在模型本身的參數擾動和測量裝置的誤差等，這些擾動通過各種途徑進入勵磁控制系統的測量環節，經綜合放大單元放大，將嚴重影響系統的控制精度[5]。因此，尋找一種算法簡單、抗干擾能力強、系統響應快、魯棒性好、易于在實際現場中應用的勵磁控制方法成為提高電力系統穩定性的關鍵。

本文將自抗擾控制技術[6]用于發電機勵磁控制系統中，該控制技術是在繼承傳統PID不依賴于對象模型優點的基礎上，通過改進傳統PID固有缺陷而形成的新型控制器。它不依賴于系統的精確模型，將模型內擾(模型及參數的攝動)和不可測外擾的作用歸結為系統的總擾動，利用非線性誤差反饋的方法對其進行實時估計并給予補償，控制對象參數發生變化或遇到不確定性擾動時都能得到很好的控制效果，具有較強的適應性、魯棒性和可操作性。在非線性強的電力系統中更顯出了其高速高精度控制的優越性。

2 自抗擾控制技術（ADRC）基本原理

2.1 ADRC的基本組成

自抗擾控制器由非線性跟蹤微分器（TD）、擴張狀態觀測器（ESO）和非線性誤差反饋控制律（NLSEF）3部分組成，其二階結構[9]如圖1所示。

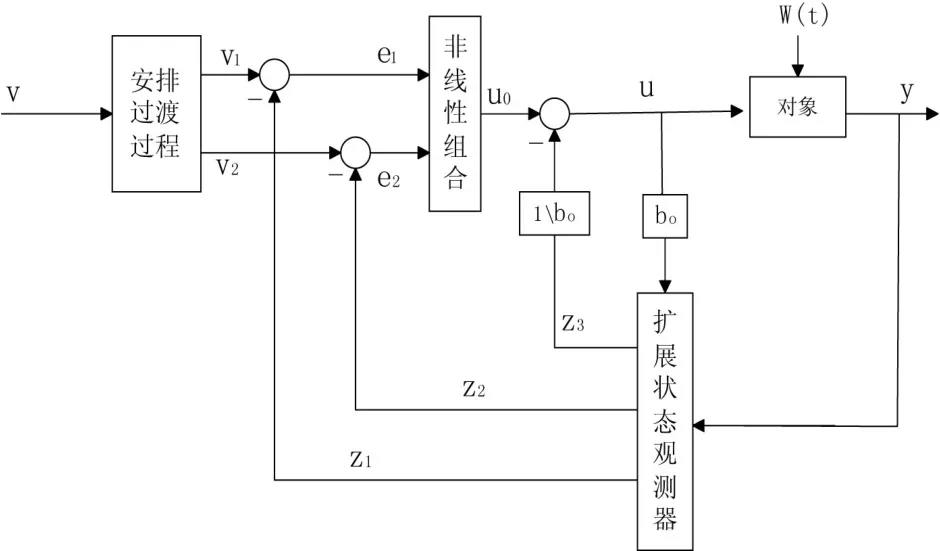
圖1 ADRC結構圖

2.2 ADRC各部分主要功能

（1）用跟蹤微分器來安排過渡過程并提取其微分信號[7]。

（2）用擴張狀態觀測器來估計被控對象狀態和不確定擾動因素，將含未知干擾的非線性不確定性對象化為積分串聯型對象進行控制，系統的“模型”和“外擾”處于同等地位，都可以用ESO估計出其實時作用量而給以“補償”。

（3）由安排的過渡過程與狀態估計之間誤差的非線性組合以及擾動估計的補償來生成控制信號，非線性反饋控制律用一個簡單的非線性函數實現了對控制工程界的經驗知識“大誤差小增益，小誤差大增益”的數學擬合，提高了自抗擾控制器的動態性能和魯棒性。

2.3 具有擾動跟蹤補償能力的二階ADRC的具體實現算法

對于這樣一類含有未知擾動w(t)的不確定對象

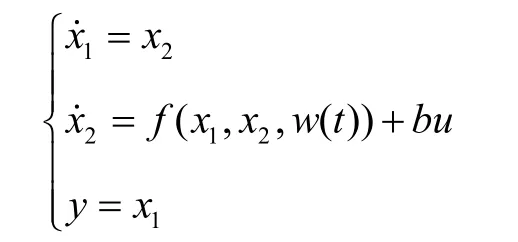
（1）設定v0為輸入，用跟蹤微分器（TD）安排過渡過程

其中，v1為v0的跟蹤信號，v2可視為v0的導數，h 是積分步長，h0為濾波因子。

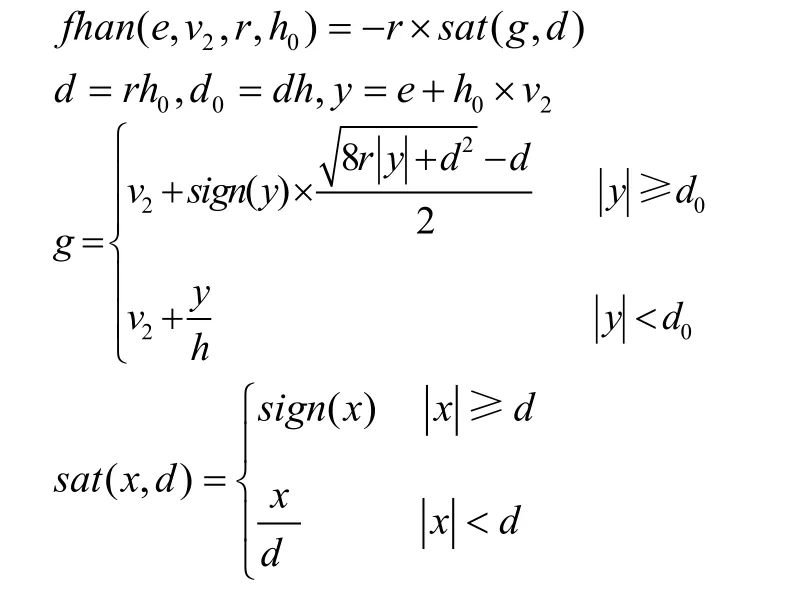
一般的控制系統中，誤差直接取成e＝v0-y，誤差的這種取法使初始誤差很大，易引起“超調”，很不合理。根據對象承受能力，若先安排合理過渡過程v1( t)，然后誤差取成e＝v1( t)-v0( t )，就可以解決常規PID控制系統的“快速性”和“超調性”之間的矛盾，并提高調節器“魯棒性”[6]。

TD的跟蹤效果及濾波性能仿真研究：

1）輸入信號v0( t)＝cos(t)時，仿真波形如圖2所示。

2）v0( t)＝cos(t)+0.1rand(1)時，仿真波形如圖3所示。

3）跟蹤誤差如圖4所示。

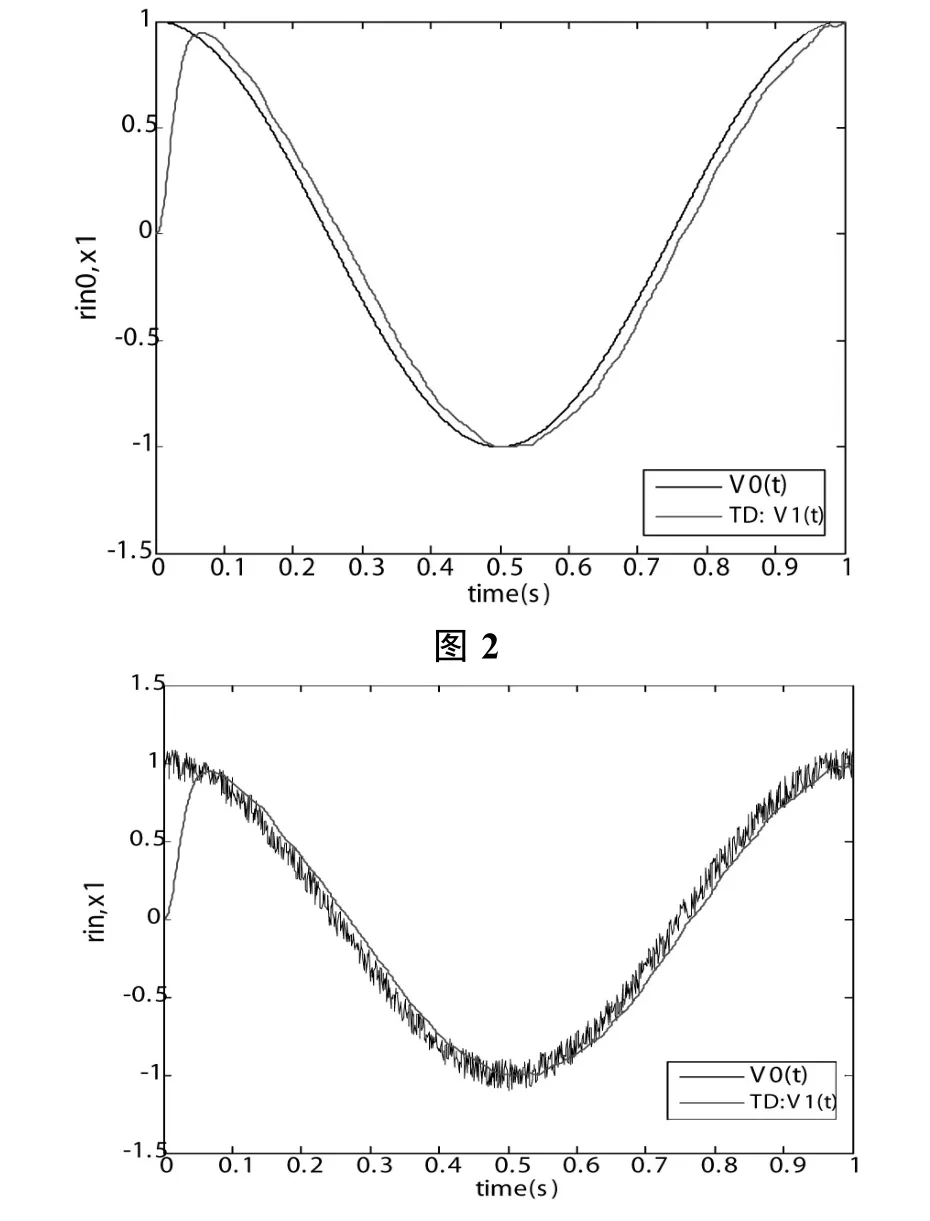
圖3

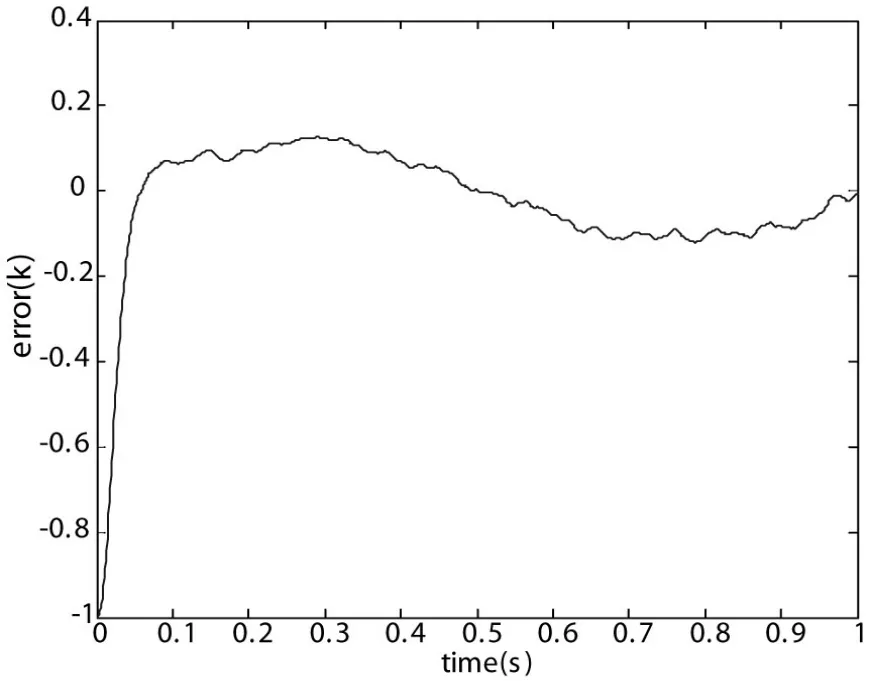
圖4

由以上仿真可知：TD具有很好的濾波效果和快速跟蹤能力。經仿真分析得出：r是決定跟蹤快慢的參數。r越大，v1更快地跟蹤信號v0，但當v0被噪聲污染時，會使信號v1被更大的噪聲所污染。為了濾掉v1所含的噪聲，選取適當的h0，能獲得很好的濾波效果。

（2）以系統輸出y和輸入u建立擴張狀態觀測器（ESO）來跟蹤估計系統狀態和擾動

文獻[9]給出了自抗擾控制技術用于濾波的研究結果，提供了一些仿真實例。結果表明，這種新型的控制技術對高頻噪聲具有較好的濾波特性。并通過應用實例與卡爾曼濾波相比， 顯示了其優越性和實用性。

3 發電機勵磁系統的自抗擾控制律設計

圖5為本文設計的存在模型參數擾動和量測誤差擾動的發電機勵磁系統方框簡圖，其中w為發電機的內部參數擾動，v為量測誤差擾動。

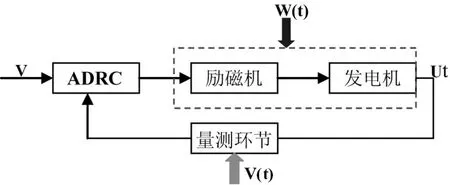
圖5 勵磁控制系統數學模型

若只研究勵磁系統動態特性，且不考慮輔助控制信號，則勵磁系統為單輸入單輸出系統，可以采用簡化的傳遞函數來表征系統各個組成部分的數學模型[10]。

（1）同步發電機傳遞函數

只研究勵磁系統的動態特性時，同步發電機的傳遞函數可以簡化為一階滯后環節

其中，KG為發電機的放大系數，為其時間常數，忽略發電機的磁場飽和現象。

（2）移相觸發單元及功率單元傳遞函數

經簡化處理，此單元用一階慣性環節來表示

（3）電壓測量環節傳遞函數

電壓測量環節由測量變壓器、整流濾波電路及測量比較電路組成。其中整流濾波電路略有延時，可用一階慣性環節來近似描述。其它電路一般可忽略它們的延時。因此，電壓測量的傳遞函數可表示為

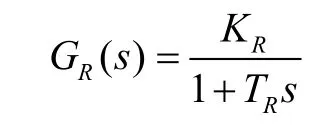
這樣得到了被控對象的控制模型。以機端電壓為控制目標，整個發電機勵磁系統可以采用二階跟蹤微分器，三階擴張狀態觀測器對勵磁系統進行自抗擾控制律設計。

4 仿真及結果分析

本文采用Matlab/Simulink仿真工具對基于ADRC的勵磁控制系統進行仿真試驗，搭建仿真圖如圖6所示。分別考慮了發電機勵磁系統分別受到突變擾動、模型擾動和測量誤差等隨機擾動時機端電壓的影響，并與經典PID的控制效果進行了比較。其中勵磁控制系統各部分參數選為：發電機轉子時間常數＝6.148s ，K＝1.0；功率單元T＝0.3s，K＝1.0；GzZ電壓測量環節TR＝0.02s,KR＝1.0。控制律中δ＝0.01，k1＝20，k2＝2。

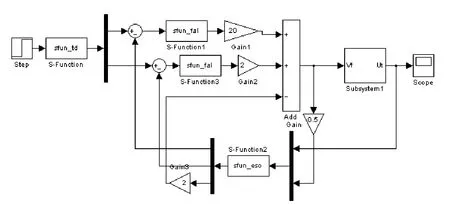
圖6

（1）在仿真進行2s時突加幅值為0.1，持續時間0.2s的方波擾動[11]，機端電壓響應如圖7所示。

（2）將勵磁系統加入方差為0.001的白噪聲w(t)作為系統模型隨機擾動時，機端電壓響應如圖8所示。

（3）將電壓測量環節加入方差為0.001的白噪聲v(t)作為系統模型隨機測量誤差時，機端電壓響應如圖9所示。

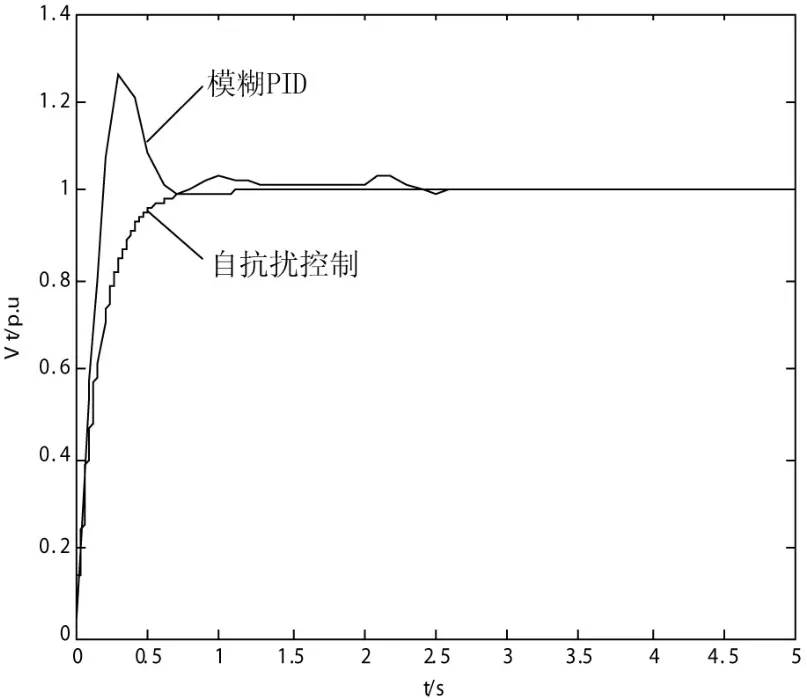
圖7 2s時加入5%階躍擾動機端電壓響應曲線

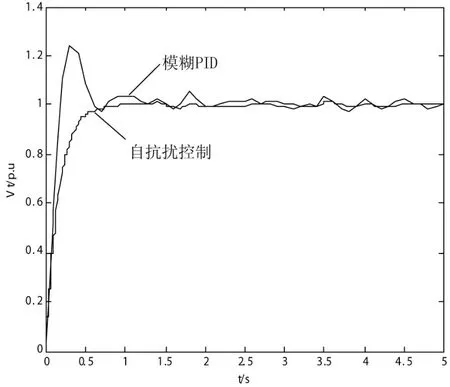
圖8 w(t)下機端電壓響應曲線

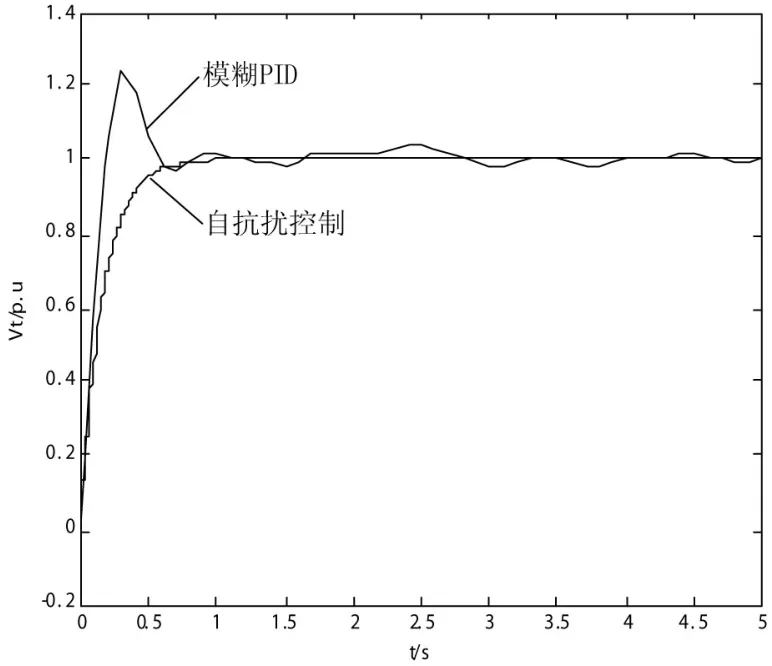
圖9 v(t)下機端電壓響應曲線

由以上仿真圖形分析可知，基于自抗擾控制技術所控制的機端電壓幾乎不受到各種隨機干擾的影響，比經典PID勵磁控制具有更好的魯棒性，從而有效改善了機端電壓的控制精度，并且系統響應快，超調小。

5 結論

基于自抗擾控制技術的勵磁系統控制策略對系統中存在的各種不確定擾動具有很好的適應性和魯棒性，有效地提高了機端電壓的控制精度，從而使電力系統的穩、準、快的性能指標都得到了改善。該控制方法算法簡單，控制效果好，是一種易于在實際現場中應用的勵磁控制方式。

[1] 萬黎,鄧長虹,陳允平.考慮機端電壓限制的多重非線性變結構勵磁控制[J].電機工程學報,2008,28(19): 86-92.

[2] 金岫,鄧志良,張鴻鳴. 基于模糊PID控制的同步發電機勵磁控制系統仿真研究[J].繼電器,2007,35(19), 13-15.

[3] 何占賓.基于微分幾何理論的發電機非線性勵磁控制的研究[D].華北電力大學碩士論文,2007.12.

[4] 劉輝,李嘯驄,韋化.基于目標全息反饋法的發電機非線性勵磁控制設計[J].電機工程學報,2007,27(1),14-18.

[5] 劉海燕.計及隨機干擾的同步發電機自動勵磁控制系統的研究[D].華北電力大學碩士論文,2005.12.

[6] 韓京清.自抗擾控制技術[M].北京:國防工業出版社,2008:243-264.

[7] 黃煥袍,武利強,高峰等.自抗擾控制在火電廠主汽溫控制中的應用[J].系統仿真學報,2005,17(1),241-244.

[8] 武利強,林浩,韓京清.跟蹤微分器濾波性能研究[J].系統仿真學報,2004,16(4):651-652.

[9] 宋金來,甘作新,韓京清. 自抗擾控制技術濾波特性的研究[J].控制與決策,2003,18(1):110-112.

[10] 孫新志.基于遺傳算法的同步發電機模糊PID勵磁控制器研究[D].西安理工大學碩士論文,2005.

[11] 揭海寶,郭清滔,康積濤等.基于模糊自調整PID控制的同步發電機勵磁研究[J].電力系統保護與控制,2009,37(9):92.