基于T-S模糊策略永磁直線同步電動機直接推力控制
楊俊友 趙 菲 劉啟宇
(沈陽工業大學電氣工程學院,沈陽 110870)
1 引言
在許多工業領域中,被控對象的運動路徑通常是直線的形式,然而長期以來人們一直借助旋轉電動機來實現直線運動。直線電動機是一種利用電能產生直線運動的電機,可以直接驅動機械負載作直線運動。永磁直線同步電動機(PMLSM)具有推力高、損耗低、電氣時間常數小、響應速度快等特點,在很多場合日益受到重視,并具有廣闊的應用前景。
直接推力控制最廣泛應用于PMLSM中,是一種具有高動態性能的新型交流伺服驅動方式[1-3],其實質是通過選擇合適的電壓矢量來迫使磁鏈逼近圓形。傳統直接推力控制無法使磁鏈形成正圓,只能使磁鏈控制在滯環中,因此直接推力控制存在著推力、磁鏈脈動大的缺點。
模糊控制技術具有語詞計算和處理不精確性、不確定性和模糊信息的能力,近年來已被證明是解決許多復雜建模和控制問題的一種有效方法[4]。T-S型模糊系統可以方便的進行非線性系統建模和非線性控制系統設計,克服了M amdani型模糊系統輸出必須解模糊的缺點。T-S模糊模型的后件輸出為線性關系,其推理方法表達記憶能力好,所得出的推理結果為清晰量,可以直接作為控制量,無須專門解模糊處理,簡化了其他模糊控制方法解模糊的過程。目前,對于T-S模糊控制的研究尚處在理論中,主要應用在轉臺控制中。
本文將T-S模糊控制策略首次應用到PMLSM直接推力控制系統,在所設計的Mamdani控制器基礎上采用辨識的方法將離散的輸出轉換為線性輸出的T-S模糊控制策略。簡化解模糊過程,改善系統的控制效果。
2 永磁直線同步電動機數學模型
不考慮端部效應的情況,根據功率不變原理可得d-q坐標系下的電壓磁鏈方程分別為[5]

其中,p=d/d t

其中,ωr=πv/τ,v 為直線電機的線速度。

電磁功率表達式為

推力Fx表示為

其中,ψPM為總磁勢
空間向量方程如下

機械運動方程

其中D為粘滯摩擦系數,W(t)為外部擾動,M為動子質量。
3 M am dani模糊控制器

圖1 基于T-S模糊控制的直接推力控制系統
3.1 磁鏈、推力的模糊化及其隸屬度函數
取推力誤差eFe與磁鏈誤差為eΨs控制器輸入

Mamdani模糊控制器采用二維輸入,一維輸出。輸入量為推力誤差eFe,磁鏈誤差eΨs,輸出量為電壓矢量對應的逆變器開關狀態[6]。將eΨs、eFe大小進行區分,根據不同等級作不同決策來優化空間電壓矢量的輸出選擇,兩個模糊變量都劃分為四個模糊子集,語言值均取為{NB,NS,PS,PB},隸屬函數選用三角形。兩個輸入量推力誤差eFe,磁鏈誤差eΨs的隸屬函數如圖2~4所示。

圖2 推力誤差隸屬函數

圖3 磁鏈誤差隸屬函數

圖4 輸出隸屬度函數
3.2 模糊控制規則及模糊決策
模糊控制器根據當前推力誤差及磁鏈誤差的模糊分級來決定是應該增大推力還是減小推力,以及是增大磁鏈還是減小磁鏈[7]。根據各個扇區所應施加的電壓矢量,可以把電壓矢量的作用分為四種:
當電壓矢量為Ⅰ時增大轉矩、增大磁鏈;為Ⅱ時減小轉矩、增大磁鏈;為Ⅲ時增大轉矩、減小磁鏈;為Ⅳ時減小轉矩、減小磁鏈。
建立16條模糊控制規則,如表1所示。
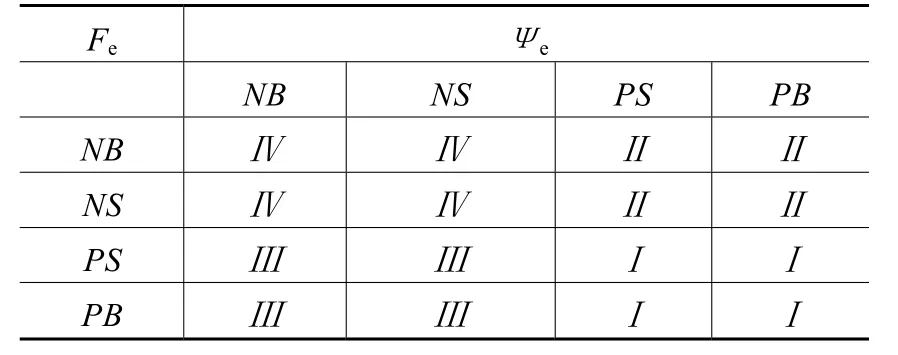
表1 控制規則表
根據這16個模糊規則構成系統總的模糊蘊涵關系R為
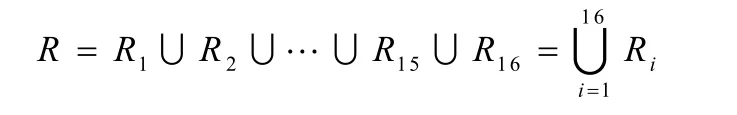
采用的模糊推理規則如下:
IF eΨs=EKi,and eFe=EFjTHEN U=Vn, i=1~4,j=1~4,n=1~6式中EKi,EFj分別為磁鏈差值、推力差值和次級磁鏈位置,Vn為單值模糊電壓矢量。

然后由測得的磁鏈差值EKi、推力差值EFj、通過模糊矩陣R可以得到電壓矢量由模糊輸出表達式

將模糊控制器的輸出與矢量表相結合,采用單點化輸出簡化解模糊過程來確定在不同的扇區應對推力轉矩及磁鏈控制作用的電壓矢量。表2為電壓矢量選擇表。

表2 電壓矢量選擇表
4 T-S模糊控制器
4.1 T-S模糊模型
T-S型模糊系統數學描述為[8]

其中,Mik,i=1,2,··,p,為模糊集,r為系統的模糊規則數目;x(t)=(x1,x2,··,xn)T∈Rn,ζ(t)=(ζ1,ζ2,··ζp)T∈Rp為模糊系統的狀態變量和前提變量;u(t)∈Rm為輸出變量。在實際的系統中,fi(x1,x2, ··xn),i=1,2, ··,r可采用多項式或狀態方程。
對于T-S類型的模糊系統,如果選擇不同的模糊推理方法以及模糊化和去模糊方法,則控制器的算法和控制效果也不相同[9]。
4.2 磁鏈、推力的模糊化及其隸屬度函數
本文中設計的T-S模糊控制器采用二維輸入,一維輸出。輸入量為推力誤差eFe,磁鏈誤差eΨs,輸出量為電壓矢量對應的逆變器開關狀態[10]。輸出表達式為u=peFe+qeΨs+k。在考慮到運算方便、性能熟悉等因素并參考專家經驗,兩個輸入量推力誤差eFe,磁鏈誤差eΨs的隸屬函數同Mamdani控制器相同。
4.3 模糊控制規則及模糊決策
為簡化解模糊過程T-S模糊控制器輸出采用系統辨識的方法來實現模糊控制器清晰化過程。二維T-S模糊控制器主要完成參數辨識。根據系統的大量輸入、輸出數據采用“最小二乘”等方法確定滿足T-S關系式的常數p、q和k的取值。采用最小二乘法所取的模糊控制器的輸入輸出進行辨識,確定出滿足T-S關系式的常數p、q和k[11]。最小二乘法是系統參數辨識中最基本最成熟的方法由數學家高斯于1795年首先提出。假定被控系統的結構如圖5所示。

圖5 一般被控系統
其數學模型可用線性方程(14)描述
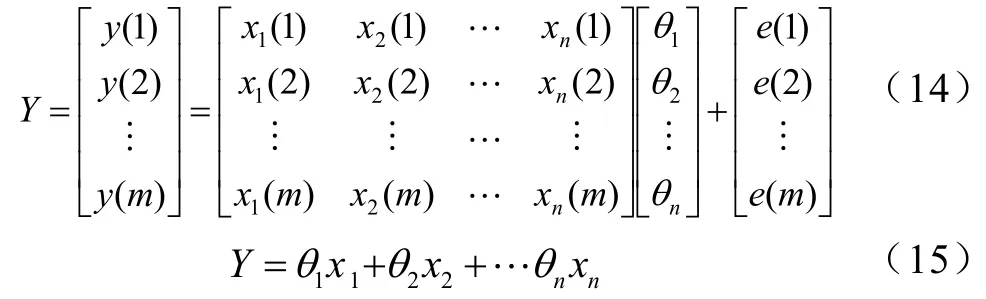
其中,Y為輸出量;x1、x2、··、xn為輸入量;θ1、θ2、··θn便是待辨識的參數。
由于實際系統存在誤差,更精確的系統模型可以表示為

若分別在t1、t2、··tm對輸入量x,輸出量y進行m次觀測,并且將系統數學模型寫成矩陣向量的形式,即

求參數θ的估計值θ∧,使性能指標J為最小,當XTX為非奇異矩陣時,可推導得被稱為參數θ的最小二乘法估計[12]。

測得一組系統參數見表1。最小二乘法參數辨識后得出p=-0.0002,q=0.0041,k=0.0000073。根據最小二乘法通過相同的辨識方法最后產生16條模糊控制規則,模糊規則見表2。

表3 所測一組系統輸入輸出參數

表4 模糊規則表
采用加權求和法求出模糊控制器的總輸出U。設第i條規則輸出的結果為ui,它的權重為ωi,則總輸出為[11]
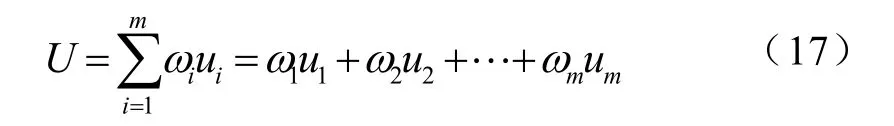
5 仿真分析
將所設計的T-S模糊控制器加入直接推力系統中,并在M atlab環境下仿真。永磁同步直線電動機參數如下:Rs=2.1?,Ld=Lq=L=16.3mH,ψs=0.211Wb,M=25kg,Ts=1μs。在該電機參數下進行帶負載仿真,負載為200N,電動機在0時刻帶負載起動,階躍輸入為0.1m/s,定子磁鏈給定為0.175Wb。仿真結果如圖5~ 9所示。

圖6 基于M am dani控制的次級磁鏈軌跡

圖7 基于T-S控制次級磁鏈軌跡

圖8 Mam dani控制策略下的速度響應

圖10 M am dani控制策略下的推力響應

圖11 基于T-S模糊策略下的推力曲線

圖12 基于M am dani模糊策略下推力曲線局部放大

圖13 基于T-S模糊策略下推力曲線局部放大
Mamdani模糊控制策略可以實現推力脈動的改良,解模糊過程隨機性大,易使系統響應發散。但是采用辨識之后的T-S模糊控制策略,將輸出又重新合理化分級細化空間電壓矢量的選擇,很好地減小推力有利的改良速度響應。系統的穩定性,魯棒性得以保證。
采取T-S模糊策略的系統次級磁鏈為圓形,在電動機空間形成了圓形旋轉磁場。其推力脈動獲得明顯改善,從而改善了其最終的輸出特性。
從仿真結果計算出速度響應的超調量為2.6%,階躍時間為0.028s,調節時間為0.044s,可以看出添加了T-S模糊控制器的永磁同步直線電機直接推力系統能夠達到輸出跟隨輸入,速度響應快。
6 結論
從仿真結果可以看出,采取T-S模糊控制策略后的直接推力控制系統的次級磁力軌跡基本為正圓形,達到直接推力控制所要求的磁鏈軌跡效果。速度響應迅速并且超調量小于5%,達到速度響應的要求。與Mamdani模糊策略相比推力響應迅速穩定,脈動得到了很好的改善,脈動明顯減小。因此加入T-S模糊策略可以改善原系統的控制效果。
[1] 鄒積浩.永磁直線同步電機控制策略的研究[D].杭州:浙江大學,2005.
[2] 葉云岳.直線電機原理與應用[M].北京:機械工業出版社,2000.
[3] 葉云岳.直線電動機技術[J].電氣時代,2002,(9): 12-13.
[4] 崔濤,趙莉.模糊控制理論和應用的發展概況[J].自動化儀表,2002,23(7):1-3.
[5] 郭慶鼎,王成元,周美文,等.直線交流伺服系統的精密控制技術[M]. 北京:機械工業出版社, 2000:44-46.
[6] 尹建寨. 直線同步電機直接推力控制方法的研究與實現 [D].四川:西南交通大學,2006.
[7] 王成.模糊系統的穩定性研究[D].武漢:武漢理工大學,2006.
[8] Tanaka K, Sugeno M. Stability analysis and design of fuzzy control systems[J]. Fuzzy Sets and Systems,1992, 45: 135-156.
[9] 修智宏,任光.T-S模糊控制系統的穩定性分析及系統設計[J].自動化學報,2004,20(2):731-741
[10] 王華, 鄒積浩, 基于模糊邏輯的直線永磁同步電機直接推力控制[J]. 電子器件, 2007, 30(6):2280-2283.
[11] 石辛民,郝整清.模糊控制及其仿真[M].北京:清華大學出版社;北京交通大學出版社,2002:118.
[12] 嚴運國,楊輝.最小二乘法參數辨識及其微機實現[J].福建電腦,20056,(6):90-92.

