Terahertz波參量振蕩器輻射THz波的理論研究

蘇新武,林 海,楊成全，徐永麗

(山西大同大學物理與電子科學學院，山西大同 037009)

THz波是指頻率在0.1-10THz(波長30μm-3mm)之間的電磁波，其波段位于微波和紅外光之間.由于THz波所處的特殊電磁波譜位置，它有非常重要的學術和應用價值.近年來由于超快激光技術的迅速發展，使THz輻射技術和應用研究得到蓬勃發展[1].日本于1997年首次實現了基于非線性LiNbO3光學參量振蕩器結構的THz電磁波參量振蕩器[2].本文從固體的元激發理論出發，運用聲子的受激散射原理闡述了THz波參量振蕩器產生THz電磁波的機理，為進一步優化THz電磁波參量振蕩器提供了理論依據.

1 TH z波產生的機理分析

固體物質系統處于基態時，晶格原子靜止在平衡位置，是一種有序的狀態.能量靠近基態的低激發態往往可以看成是一些獨立的基本激發單元的集合，這些基本激發單元稱為元激發[3]，對此可用不同的能量載子把它量子化.晶體在光的作用下，使系統處于激發態，原子偏離平衡位置做微小振動.對于晶體，由于存在周期性振動，原子小振動的集體運動用格波來表示.由于每個格波的能量取值是可以量子化的，這些能量載子就是聲子，它是固體中典型的元激發.聲子包括聲學聲子和光學聲子，相應的格波分別為聲學波和光學波，而光學波對于離子晶體的情形是極化波，極化波則引起固體內部的電極化，使入射光發生散射;這種散射稱為喇曼散射.

圖1 電磁耦合場量子的色散曲線

當抽運激光束入射到極性LiNbO3晶體時將會激發產生光學波.對于晶體中激發的光學波既可以由喇曼過程來激發，又可以由紅外吸收過程來激發.因為橫振動的長光學波Q(長光學橫波)伴有電磁場.于是，當強度足夠大的抽運激光射入晶體時，光波就會和晶體中的長光學橫波相互作用、相互耦合，產生的混合激發波就是所謂的電磁耦合場量子，或稱為極化聲子[4～6](Polariton)，它服從聲子色散曲線.圖1為電磁耦合場量子的色散曲線.電磁耦合場量子具有兩重性，既具有晶格振動的特征又有電磁振動的性質.從圖中可知耦合場振蕩在波長很小范圍內，耦合場振蕩主要保持著晶格振動的特征，此時電磁耦合場量子主要是TO聲子的性質，耦合場振蕩在波長很長范圍內，主要保持著電磁振動的性質，電磁耦合場量子主要是光子的性質，也就是說在能量較大的范圍內主要是喇曼散射過程.相反能量較小范圍內主要是參量發生作用的過程.在這一過程中便會產生在THz頻率范圍的電磁波也就是THz波和斯托克斯光.在這里我們把斯托克斯波定義為閑頻波(idler)，THz波叫做信號波.在斯托克斯波和THz波通過參量產生的過程中，它們的頻率由能量守恒ωP=ωT+ωi和相位匹配條件kP=kT+i所確定，如圖2所示.

圖2 相位匹配條件

2 TH z波增益計算

受激極化聲子散射這一過程可看作是參量產生過程和受激喇曼過程的組合[7～10]，在這些過程中它涉及四個相互作用的波:抽用光EP，閑頻光Ei，信號光ET和橫光學格波.假設這些光波都為平面波，則光電場都能分解為無限大平面波的集合，則有:

在穩態情況下它分別服從波動方程和格波力學方程:

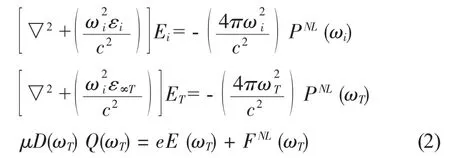
假定在波與波相互作用的過程中存在一個有效相互作用能:

(3)式中N是介質晶體中原胞的密度，dE表示二階參量過程的非線性系數，dQ表示三階喇曼散射過程的非線性系數.非線性極化強度PNL和非線性力FNL由下式給出

閑頻光和THz光的增益分別定義為

方程有解的條件是特征方程為零，把此特征方程展開，忽略γ的二次項有:

閑頻波的復線性波矢可表示為:

其中，Δki=ki-kiL為相位匹配量.同理可得:

將式(7)(8)(9)帶入(6)式得:

在相位匹配時有Δk=0，LiNbO3晶體對于斯托克斯光來說幾乎是透明的則有THz波在LiNbO3晶體中的吸收系數較大，定義因為閑頻光和抽運光的夾角很小且它們間的關系為gT=g cos φ ? cos φ，則式(10)可表示為:

由于方程(11)左邊為實數，則方程右邊的虛部應為零，方程右邊的實數部分定義為在沒有損失的情況下的參量增益g0，則有

其中，

解方程(12)得

則THz波的增益應為

3 結論

運用Henry和Garrett的波耦合方法并考慮了LiNbO3晶體對THz波的吸收損失，給出了THz波參量增益式的詳細推導過程，得出了THz波參量增益計算式.為進一步研究THz電磁波參量振蕩器提供了理論依據.

[1]王少宏，許景周，汪力，等.THz技術的應用及展望[M].物理，2001，30:612-615.

[2]Yuuki Watanabe，Kodo Kawase，Tomofumi Ikari.Spatial pattern separation of chemicals and frequency independent components by terahertz spectroscopic imaging[J].Applied Optics，2003，42(85):5744-5748.

[3]方俊鑫，陸棟.固體物理學(下冊)[M].上海:科學技術出版社，1981:190-202.

[4]M·卡多納.固體中的光散射[M].北京:科學出版社，1986:326-331.

[5]石順祥，陳國夫，趙衛，等.非線性光學[M].西安:西安電子科技大學出版社，2003:273-274.

[6]Shen Y R.Nonlinear Infrared Generation[M].New York:Springer Verlag Berlin Heidelberg，1977.

[7]Sussman S S.Tunable light scattering from transverse optical modes in lithium niobate.Stanford[J].CA:Microwave Lab，Stanford University，1970:1851.

[8]Henry C H，Garrett C G B.Theory of Parametric Gain near a Lattice Resonace[J].Phys Rev，1968，171(3):1058-1064.

[9]Barker A S，Loudon J R R.Response functions in the theory of Raman scattering by vibrational and polariton modes in dielectric crystals[J].Rev Mod Phys，1972，44:18-47.

[10]Schwartz U T，Max Maier.Damping mechanism of phonon polaritons，exploited by stimulated Raman gain measurements[J].Phys Rev B，1998，58:766-775.

[11]Junichi Shikata，Kodo Kawase，Manabu Sato，et al.Characteristics of coherent terahertz wave generation from LiNbO3optical parametric oscillator[J].Electronics and Communications，1998，J81-C-1(5):267-273.