理想變壓器特性方程教學方法討論

陳希有,劉鳳春,董維杰,李冠林

(大連理工大學電氣工程與應用電子技術系,遼寧 大連 116023)

理想變壓器是電路理論課的必學內容。作為一種理想化的電路元件,理想變壓器在建立電路模型、分析電路行為和綜合網絡函數等研究中發揮重要作用。在“電機與拖動”等后續課程中,變壓器是重要內容之一。因此,教學中應使學生透徹理解理想變壓器主要特性以及這些特性的電磁學基礎和理想化條件等。目前,對理想變壓器特性的描述主要有三種典型方式:直接給出定義[1-3］、對線性互感進行理想化[4-6］和對實際變壓器進行理想化[7］。本文對比分析了這三種教學方式的特點,詳細討論了理想變壓器特性方程在不同導出背景下的理想化假設條件。期望借助此文與讀者展開更多交流。

1 用直接定義闡述理想變壓器的特性

這種方式類似于定義電阻元件一樣直接定義理想變壓器特性:滿足下列代數關系的二端口元件稱為理想變壓器,并用圖1表示。

式中,n稱為理想變壓器的變比或電壓比,是理想變壓器的唯一參數。

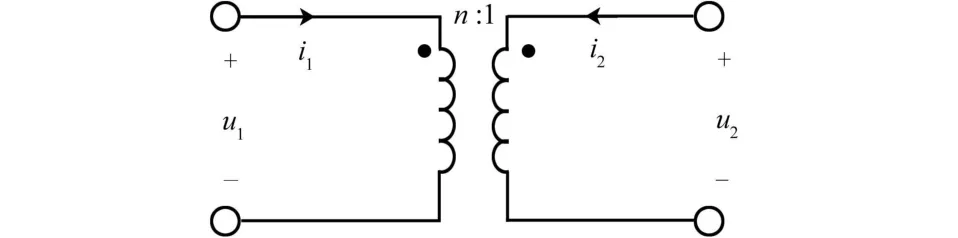
圖1 理想變壓器的符號

這種教學方式可以直接觸及教學要點,在教學時數較少的情況下是一種能夠有效節省時間的教學方法。但在教學實踐中常會遇到如下質疑:

(1)理想變壓器與互感特性完全不同,為什么使用相似的符號?

(2)定義中沒有涉及電磁關系,那么如何理解同名端的涵義?

(3)變比等于匝數比,在沒有實際變壓器做原型的情況下,怎樣解釋匝數和匝數比?

(4)它既不儲能又不耗能的特性只能根據功率的計算結果得出,即

對這種特性的物理機理的解釋更是難以講清,只能強制學生暫時接受。

(5)在理想變壓器之前已介紹了理想電阻、理想電感、理想電壓源和理想電流源,它們都與實際電阻、實際電感、實際電壓源和實際電流源建立了密切的內在聯系。相比之下,學生會問到理想變壓器與實際變壓器存在怎樣的內在聯系?

采用這種直接定義的方式,教師一時難以回答學生的上述質疑,要待到學習磁路或變壓器時才能漸漸解釋清楚。

2 對線性互感進行理想化

為避免使用直接定義導致高度抽象的教學弊端,一種可取的方法就是在線性互感模型的基礎上做進一步抽象。在講授互感時已建立了互感的電磁關系,如圖2所示,其電路符號如圖3所示。

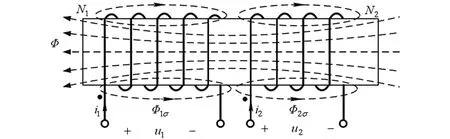
圖2 線性互感電磁關系示意圖

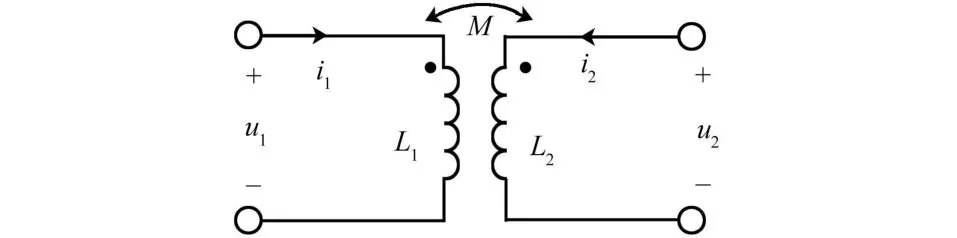
圖3 互感符號

為闡明理想變壓器特性方程的假設條件,需簡述線性互感特性方程的建立過程。

我們如果忽略介質的渦流損耗,假設耦合線圈周圍為線性磁介質,則每個繞組的總磁鏈等于自感磁鏈與互感磁鏈的代數和,這些磁鏈均與激發它們的繞組電流成正比,即

再忽略導線銅損,并根據磁通的交鏈關系和電磁感應定律,便得到如下特性方程組:

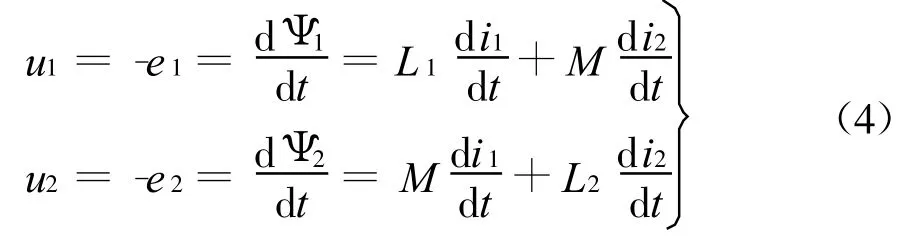
這一關系建立在電磁感應定律基礎上,有明確的物理意義。它成立的必要條件是:線性無損磁介質和不計導線銅損。

我們可進一步解釋如下:如果存在磁滯損耗,則介質便是非線性介質,磁鏈與激發它的電流不成正比,總磁鏈也不能用疊加的方法來計算;如果存在渦流損耗,則式(3)中的磁鏈還應包含渦流產生的磁鏈。由于渦流是感應電動勢產生的,所以渦流不是與磁鏈成正比,而是與磁鏈的時間變化率成正比。故此時總磁鏈不能僅表達成線圈電流的線性組合,還應包含電流的時間導數,但此時磁鏈與線圈電流仍屬線性關系。

據此推理:對線性磁介質,雖然在直流工作時,滿足式(3)的磁鏈與電流關系,但在交流工作時,如果有渦流損耗,卻不滿足式(4)的電壓與電流關系。

對線性互感進行理想化以便建立理想變壓器的過程一般可按如下條件考慮[4］。

理想化條件一:忽略線圈漏磁,即全耦合,耦合系數k=1,互感系數為

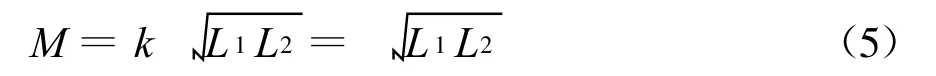
這將導致式(4)中的系數行列式L1L2-M2=0,則兩式不再獨立,u1和u2必然存在內在聯系。為尋此聯系,將式(5)代入式(4),可得

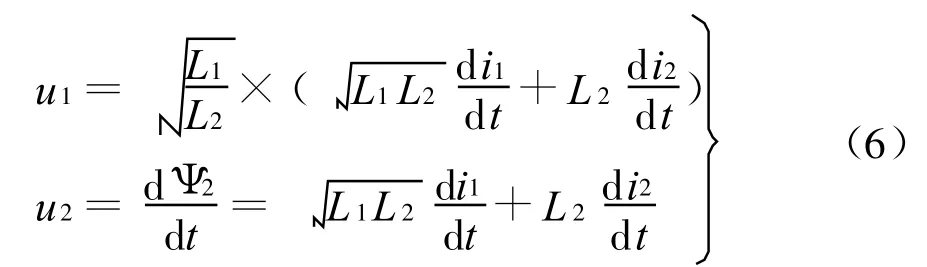
比較上述兩個電壓關系式,便得

再由電感與匝數的平方正比關系,可得

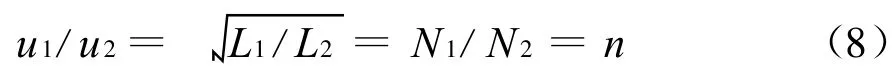
上式便是理想變壓器的特性方程之一,即電壓變換關系,它表明了u1和u2的內在聯系。

由于上述關系是基于線性互感得到的,所以會自然想到,式(8)成立的必要條件應是:線性無損磁介質(磁導率不一定是無限大)、全耦合和無銅損。而事實上,式(8)的成立并不需要滿足線性無損磁介質的條件,只需滿足全耦合和無銅損條件。這便產生了不一致的結論。見下節分析。

理想化條件二,兩自感同比趨于無限大,比值等于匝數比的平方,即

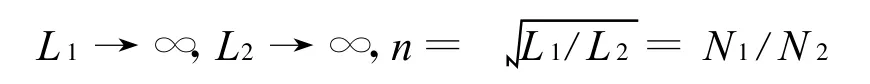
將上述條件代入互感方程(4)得

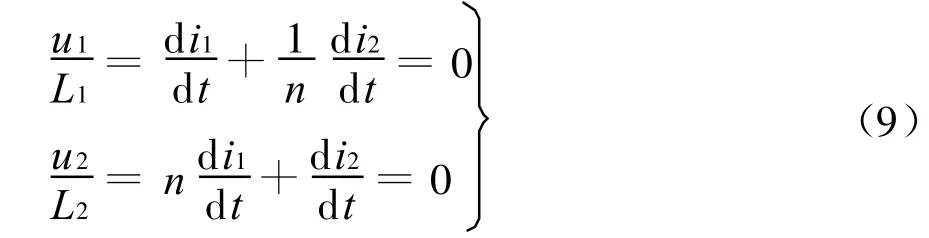
根據上述方程組中的任意一個方程都可得到

再計算從-∞到t的定積分得

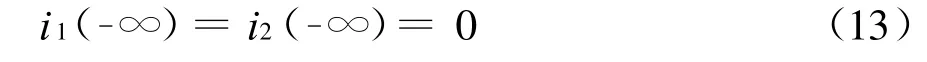
由式(12)和式(13)得到理想變壓器的電流變換關系為

式(14)要求自感趨于無限大,在匝數和尺寸一定的條件下,只能是磁導率趨于無限大。亦即自感趨于無限大的假設等同于磁導率趨于無限大的假設,而無限大磁導率的磁介質可視為線性磁介質的一種極端情況。

所以,基于上述對互感的理想化過程得出理想變壓器電流變換關系的必要條件是:無損耗、全耦合及磁導率為無限大。

這個條件包括了電壓變換所需要的條件,也就是說電流變換所需條件比電壓變換所需條件來得更嚴格一些。故這個條件也就是基于線性互感推理得到的理想變壓器的理想化條件。

上述過程將理想變壓器建立在線性互感基礎上,使理想變壓器有了確定的物理原型,并且建立了這兩種電磁耦合元件的內在關系。但是從過程上看,仍然不易解釋理想變壓器為什么不能儲存能量?為什么理想化后互感的儲能特性消失了?在理想化過程中要保持n,對此也缺少說理性。

3 對實際變壓器進行理想化[7］

實際雙繞組變壓器通常是用良導體做成的兩個線圈繞在同一個磁導率很大的鐵磁材料即鐵心上制成的,如圖4所示。

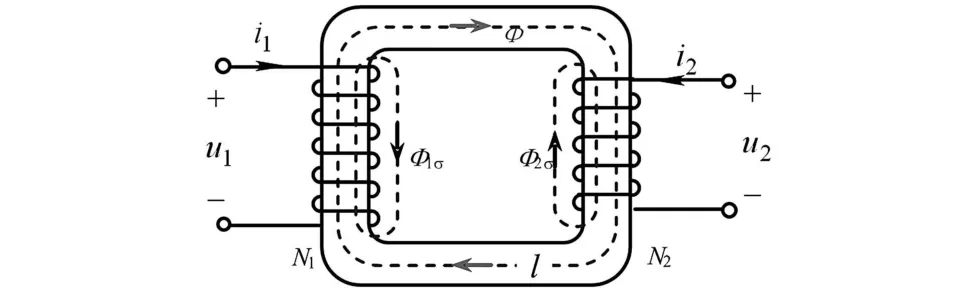
圖4 實際變壓器電磁關系示意圖

由于高導磁材料的存在,線圈電流所激發的磁通主要集中在鐵心內部,線圈漏磁通 Υ1σ和Υ2σ相對很小。

1)理想化第一步是忽略線圈漏磁和銅損。這樣,每個線圈的磁鏈 Χ1和 Χ2分別等于其匝數N1和N2與鐵心內磁通Υ的乘積,即

2)理想化第二步認為線圈無銅損。這樣,各線圈端口電壓等于感應電動勢的負值,按照圖4中的參考方向得

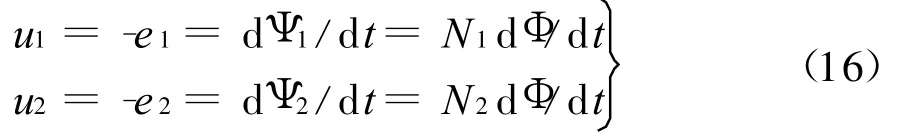
由式(16)便得理想變壓器的電壓變換關系,即

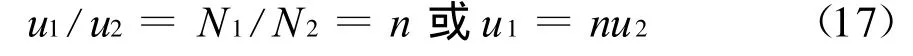
從上述過程看,電壓變換關系成立的必要條件是線圈全耦合和無銅損。對是否存在鐵損和介質是否為線性介質沒有要求,而從互感推演時,需要線性無損介質。可見,從不同途徑推導,需要不同的假設。

3)理想化第三步認為鐵心的渦流損耗為零。于是,在圖4中沿路徑l應用安培環路定律得

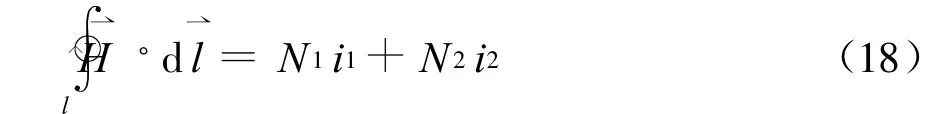
需要注意的是:如果存在渦流,則式(18)右邊還應包括渦流產生的磁動勢,這樣便得不到理想變壓器的電流變換關系。

4)理想化第四步認為介質磁導率μ※∞,(從而不存在磁滯現象。如果存在磁滯,則磁導率不會始終為無限大)。則鐵心內磁場強度為

所以磁場強度沿閉合路徑的積分結果為

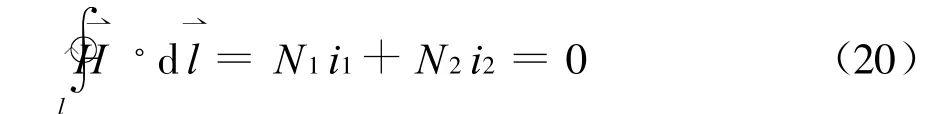
這樣便自然得到理想變壓器的電流變換關系為

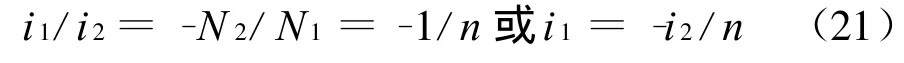
式(20)清楚表明,電流變換關系成立的必要條件是磁導率μ※∞(不需勵磁電流)和不計渦流損耗,它并不需要全耦合和忽略線圈銅損的條件。所以理想變壓器的電壓變換關系和電流變換關系所需的假設條件是不同的,且二者不存在包含關系。

利用上述電磁原理來理解理想變壓器的非儲能特性也是很簡單的。因為在μ※∞假設下,磁場能量密度變為

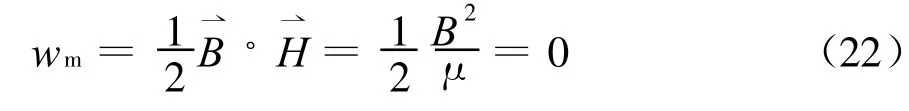
這很好地說明理想變壓器雖然存在線圈以及磁感應強度和磁通,但它卻是非儲能元件。

將電壓和電流變換關系合在一起,得到從實際變壓器到理想變壓器的理想化條件為:無損耗、全耦合及磁導率為無限大。

還需說明,無限大磁導率并不意味著全耦合,全耦合也不一定需要無限大的磁導率。所以,后兩個條件是獨立的。

第三種教學方法所涉及的電磁學原理,在大學物理課中已經奠定了相應的基礎。所以,這種教學方法可以使得不同課程內容之間融匯貫通,能夠加深對理想變壓器物理背景的理解。也能較好地處理第一種方法中遇到的質疑。不足之處是所需教學時間較長,涉及到的基本概念較多。

4 和磁路教學呼應

對大部分電氣工程及其自動化專業的學生來說,在電路理論課中還要學習磁路知識。在學習過程中,嚴格地建立了圖5所示的實際雙繞組變壓器的相量等效電路,其中含有理想變壓器。通過令某些等效參數為零,便可得到理想變壓器方程。銅損且繞組為全耦合,則得到理想變壓器的電壓變換方程。

圖5 雙繞組變壓器等效電路

若令G0=0,B0=0,,即不計鐵損且磁導率μ為無限大,則得到理想變壓器的電流變換方程﹒I1=﹒I2/n 。

這又一次說明了電壓變換方程和電流變換方程所需要的假設條件是不一樣的。

從上述得到的理想變壓器假設條件是:①忽略功率損耗;②全耦合;③磁導率無限大。呼應了第3節的結論。

由于圖5是實際變壓器的相量模型,所以在上述假設條件下,理想變壓器特性方程的相量形式是成立的,在任意時變電壓和電流條件下是否還存在這樣的變換關系,對此缺少說理性。相比之下,第3節的教學方法卻沒有這樣的質疑,因為第3節的電壓變換關系和電流變換關系是在滿足假設條件的基礎上,基于基本的電磁規律建立的。

5 結語

本文對比分析了時下常用的理想變壓器特性方程的三種教學方法及其特點。可根據專業性質、教學時數、教學基本要求及教師個性等選擇其一講授。在后兩種方法中,雖然電壓變換關系的必要條件不同,電流變換關系的必要條件也不同,但將兩個變換關系進行綜合,得到理想變壓器的必要條件卻是一致的。

理想變壓器雖然屬于經典的電路理論內容,但對其所采取的教學方法仍值得努力探索,愿以此拋磚引玉,并希望得到讀者的積極反饋。

本文在成稿過程中,中國工程院院士俞大光對變壓器的理想化步驟提出了有益建議;北京航空航天大學雷銀照教授對磁介質的性質問題給出了詳細解釋。他們的基本觀點都被作者所采納。在此,對二位老師的熱情幫助表示由衷的謝意。

[1］燕慶明.電路分析教程(第2版),北京:高等教育出版社,2007年6月

[2］陳洪亮,張峰,田舍平.電路基礎,北京:高等教育出版社,2007年5月

[3］李瀚蓀.電路分析基礎(第四版(下冊)),北京:高等教育出版社,2006年5月

[4］邱關源.電路(第四版),北京:高等教育出版社,1999年6月

[5］于歆杰,朱桂萍,陸文娟編著.電路原理,北京:清華大學出版社,2007年3月

[6］董維杰,白鳳仙.電路分析,北京:科學出版社,2007年8月

[7］陳希有.電路理論基礎(第三版),北京:高等教育出版社,2004年1月