基于Markov理論的反艦導彈突防艦載防空火炮效能評估

韓 維，張華宇，岳奎志，史建國

（1.海軍航空工程學院 七系，山東 煙臺 264001；2.海軍專項工程辦公室，北京 100085）

反艦導彈對艦艇的攻擊是一個復雜的過程。首先，要成功發射反艦導彈；其次，要突防防空導彈的攔截；再次，要突防n座艦載防空火炮的攔截。在兩種突防過程中，還伴隨著軍艦上有源電子干擾和無源電子干擾對反艦導彈制導的影響。所以，作戰時1枚反艦導彈成功擊中1艘軍艦是非常困難的，這就需要探討m枚反艦導彈同時攻擊1艘軍艦的“飽和”攻擊戰術問題，而m枚反艦導彈突防n座防空火炮是反艦導彈攻擊軍艦的一個重要環節，也是軍艦末端防御環節，具有一定的軍事研究價值。以往研究突防效能評估模型，常使用概率法、層次分析法、排隊論法、蒙特卡羅法等[1-4]，各有優缺點，但這些方法共同存在的不足是缺少動態性，而采用Markov 理論[5-6]就能動態地評估m枚反艦導彈隨時間、距離、海況變化情況突防效能，該方法被廣泛地應用在作戰效能分析的各方面。

1 預備知識

本文所采用的馬爾可夫模型是一個在作戰模型建模中經常應用的一種隨機過程模型。

一個隨機過程，如果對于每一時刻 t0，系統未來處于任何狀態的概率僅與當時（t=t0）的狀態有關，而與系統是怎樣和何時進入這種狀態無關，這種隨機過程為馬爾可夫隨機過程。

1.1 馬爾可夫鏈

馬爾可夫鏈數學表達式：

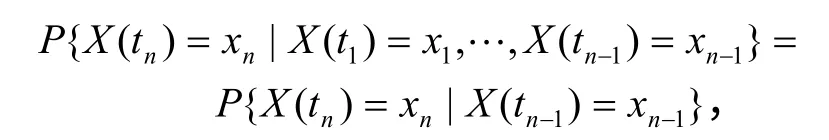
式中：X (ti)=xi表示處于 ti(i=1,2,…,n)時刻的狀態。馬爾可夫具有的這種性質，稱為馬氏性，或稱為無后效性。

若馬爾可夫鏈X(t)，從t時處于狀態i，轉移到t+?t時處于狀態j的轉移概率與轉移的起始時間t 無關，為：

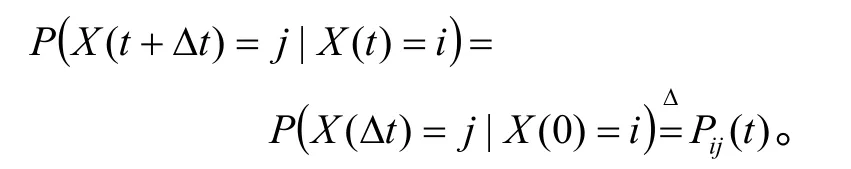
把Pij(t)排成的矩陣 P(? t)=[pij(t)]成為馬爾可夫鏈狀態概率轉移矩陣，在此有：

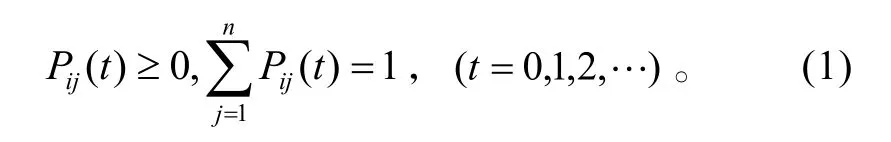
1.2 吸收馬爾可夫鏈

為了研究方便，進行如下假設：①組成系統單元的毀傷率的分布為服從λ指數分布；② X (t)表示系統在時刻t的狀態；③ 每個單元無論處于什么狀態都是相互獨立的。

Pij=1的狀態稱為吸收狀態。若馬氏鏈中至少含有一個吸收狀態，并且從每個非吸收狀態出發都可以達到某個吸收狀態，則稱為吸收馬氏鏈。

則X(t)是一個吸收馬爾可夫鏈。假定單元的毀傷率為λ。根據狀態轉移圖1，可寫出馬爾可夫鏈狀態概率轉移的矩陣P(?t)，即：

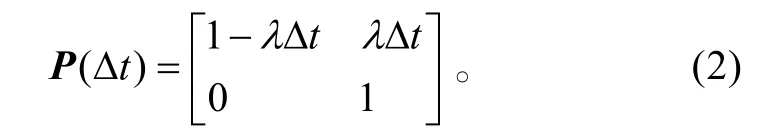
在 ?t時間內馬爾可夫鏈狀態轉移方程為：

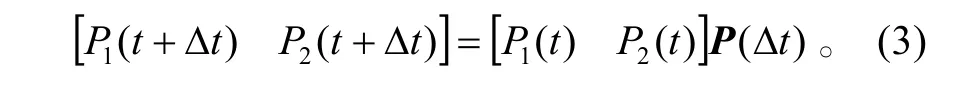
圖1 吸收馬爾可夫鏈狀態轉移圖

2 分析模型

2.1 導彈突防防空火炮的Markov模型推導

設反艦導彈初始m枚，其進入帶有n座近程防御火炮的軍艦射擊范圍內，λ為反艦導彈被擊毀的概率。則反艦導彈突防防空火炮的吸收馬爾可夫鏈狀態模型如圖2所示，圖中 i=m,m ?1,…,1,0分別代表在突防過程中有 m,m? 1,…,1,0枚導彈生存；在 ?t時間段內有n座防空火炮一起射擊來襲導彈，反艦導彈的毀傷概率為nλ ?t；1? nλ ?t代表該時間段內狀態空間為i的反艦導彈的生存概率。

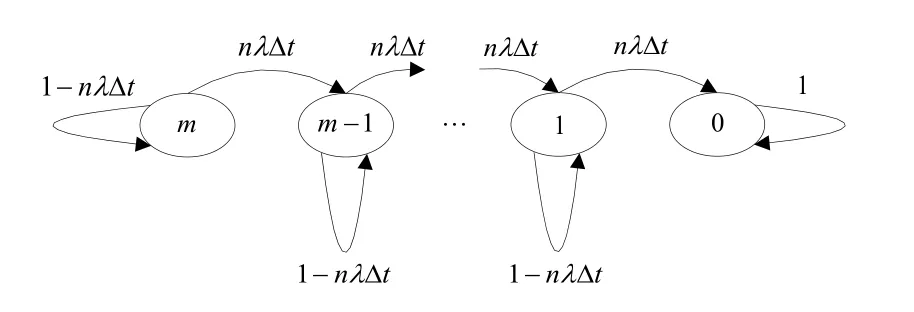
圖2 突防防空火炮的吸收馬爾可夫鏈狀態轉移圖

令Pi(t)(i=m,m ? 1,…,1,0)表示t時刻狀態空間為i的概率。

開始時t=t0，當 t=t0+?t時導彈突防成功的概率等于導彈在t=t0時沒有被擊毀的概率Pi(t)，減去n座防空火炮擊毀導彈的概率Pi(t)nλ ?t，即同理可得：

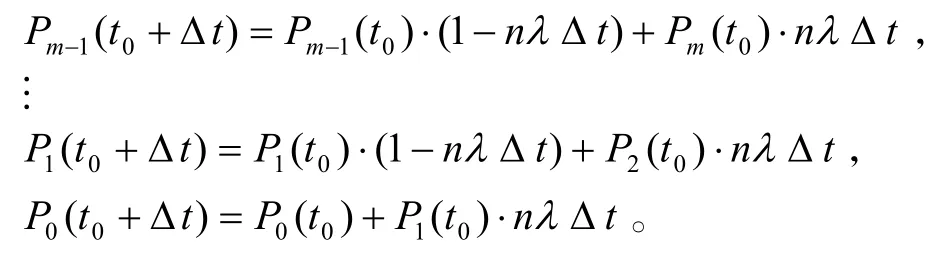
歸納起來，得出不同時間點狀態空間中各狀態概率：

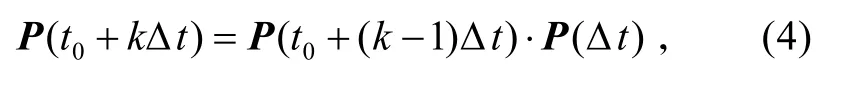
式中：

由式(4)可知，這是一個典型的吸收馬爾可夫鏈模型。

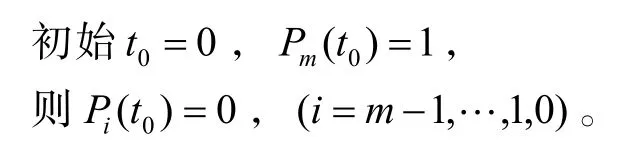
某時刻反艦導彈突防的數目等于各個狀態的導彈數目與相對應狀態概率的乘積，即：

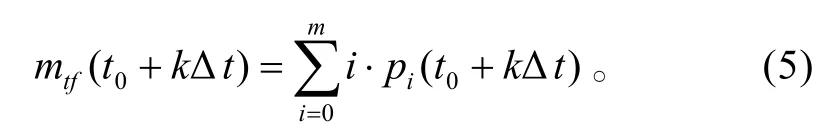
某時刻反艦導彈被擊毀的數目為：

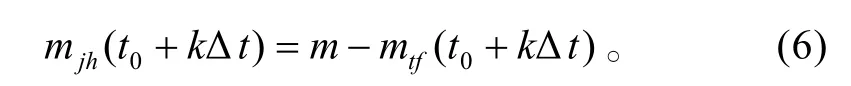
某時刻反艦導彈突防軍艦的防空火炮的效率：

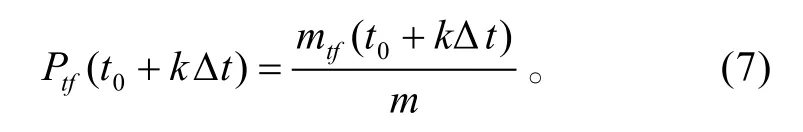
2.2 反艦導彈被火炮擊毀概率

反艦導彈被擊毀概率λ為：

式中：DP為反艦導彈被探測的發現概率；PH/D為發現后被擊中的條件概率；PK/H為彈丸擊中反艦導彈后導彈被毀傷的條件概率。

2.3 考慮海況等級下反艦導彈被火炮擊中概率

軍艦在航行中，海浪會導致艦體縱搖、橫搖、垂蕩等運動，嚴重影響艦上防空火炮的射擊精度。艦船的傾斜和搖擺環境除了與風浪大小有關外，更重要的與艦船設計的穩定性有關[7]。

在不同海況等級條件下，海浪對艦體搖擺導致防空火炮彈丸的散布角度為

式中：?為炮彈丸的散布角度（°）；f為射擊精度修正系數，一般取0.9；υ為海況等級，作戰條件下，海況等級取1～5。

防空火炮發射的密集彈丸分布是一個圓錐形區域，如圖3所示。

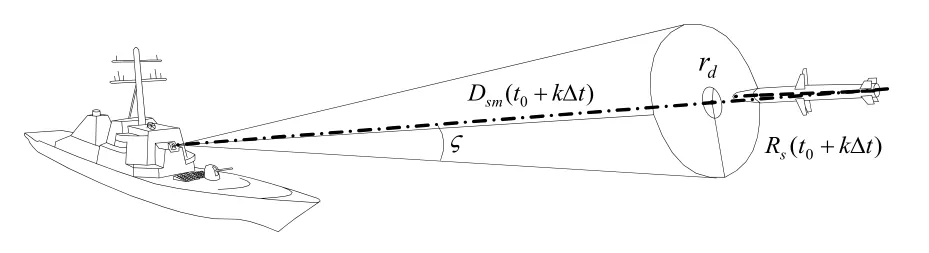
圖3 防空炮彈射擊空間示意圖

設反艦導彈超低空勻速飛向軍艦，導彈有效被攻擊截面積可視為半徑為rd的圓形，并且導彈以勻速 vdd飛向目標，軍艦上每座防空火炮的射速為ρk，彈丸的散布角度為?，設彈丸服從均勻分布，防空火炮最大有效射擊距離為Dmax，最小有效射擊距離為Dmin。

反艦導彈在 t=t0+k?t (k=0,1,…,nn)時刻突防軍艦的距離為：Ltfm(t0+ k?t)=vddk?t。

反艦導彈在 t=t0+k?t(k=0,1,…,nn)時刻距離軍艦的距離為：

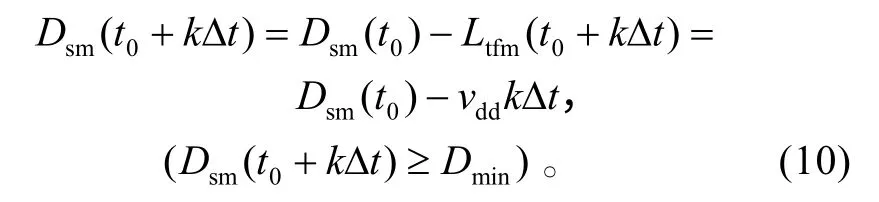
最大時間點nn為：

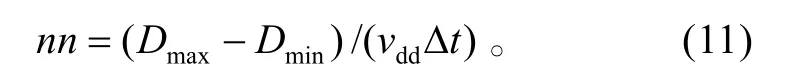
在t=t0+k?t時刻防空火炮發射的彈丸在距離軍艦 Dsm(t0+k?t)點處的誤差半徑為：

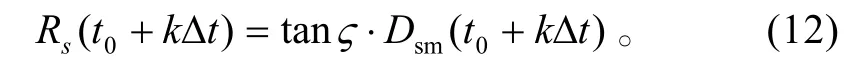
在t=t0+k?t時刻防空火炮發射的彈丸命中導彈的概率為：

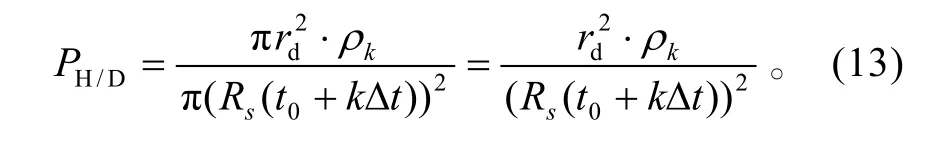
3 仿真實例

設初始時刻 t0=0，Dsm(t0)=4km，X1型反艦導彈速度1 000 m/s，X2型反艦導彈速度300 m/s，防空火炮最小有效射擊距離 Dmin=500 m，導彈半徑rd=0.18 m，每座防空火炮射速 ρk=75 發/秒（4 500發/分），軍艦上有防空火炮座數為n=2，反艦導彈被艦炮命中1 發后其毀傷概率 PK/H=0.5，反艦導彈被探測到的概率 PD=1。則反艦導彈突防軍艦近程防空火炮的仿真結果如下。

如圖4所示，海況等級越高，導彈突防效率越高；海況等級越低，導彈突防效率越低。當海況等級為1級時，單發X1型反艦導彈到距離軍艦500 m止，突防2座防空火炮效率為59.9%；其他條件相同，當海況等級為2級時，X1型導彈突防效率為82.8%，當海況等級為3級時，X1型導彈突防效率為93.3%，當海況等級為4級時，X1型導彈突防效率為97.5%，當海況等級為5級時，X1型導彈突防效率為99.1%。由此可知，海浪對艦船搖擺直接影響軍艦上防空火炮的射擊精度。

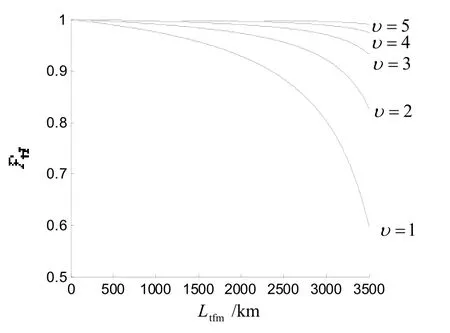
圖4 不同海況等級條件下單發X1型反艦導彈突防軍艦上2座防空火炮的效率

如圖5所示，反艦導彈速度越快，導彈突防效率越高。當海況等級為1級時，單發X1型反艦導彈到距離軍艦500 m 止，突防2座防空火炮效率為59.9%，單發X2型反艦導彈到距離軍艦500 m 止，突防2座防空火炮效率為18.1%。由此可知，超音速反艦導彈比亞音速反艦導彈突防效率高。

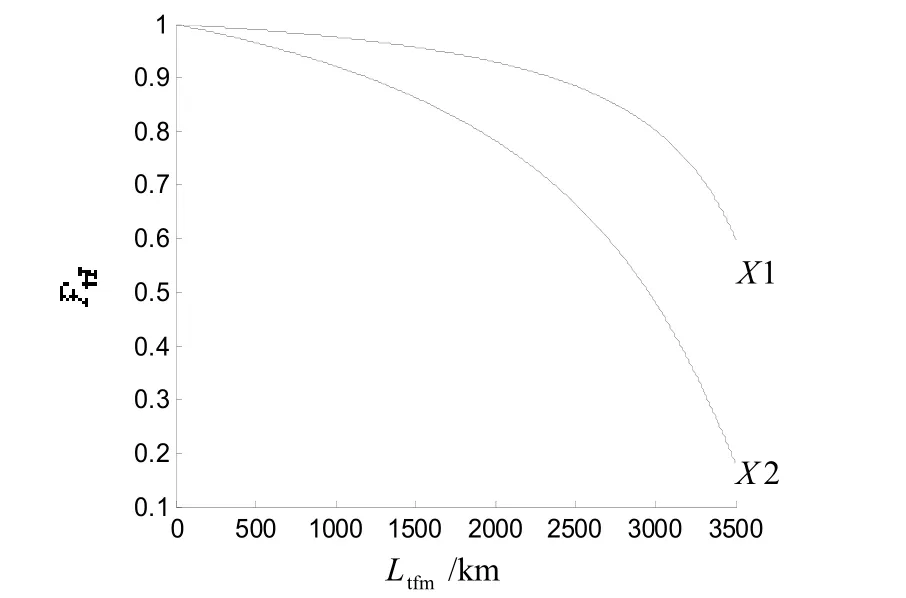
圖5 在1級海況等級條件下單發X1、X2型反艦導彈突防軍艦上2座防空火炮效率

從圖6、7可知，導彈突防防空火炮效率隨反艦導彈枚數不同而不同。X2型反艦導彈為1枚時，突防效率為18.1%；X2型反艦導彈為2枚時，突防效率為33.5%；X2型反艦導彈為3枚時，突防效率為47.5%；X2型反艦導彈為4枚時，突防效率為58.3%；X2型反艦導彈為5枚時，突防效率為66.0%。由此可知，反艦導彈數量越多，突防防空火炮效率高。

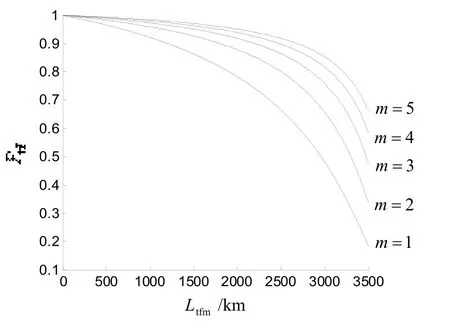
圖6 在1級海況條件下m枚X2型反艦導彈突防軍艦上2座防空火炮效率

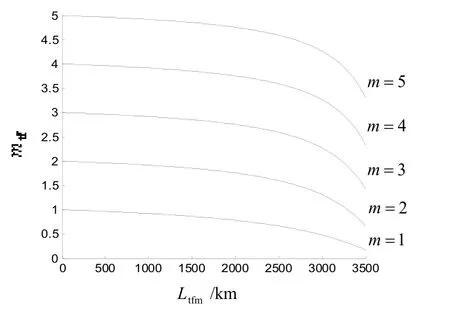
圖7 在1級海況條件下m枚X2型反艦導彈突防軍艦上2座防空火炮突防枚數

在保證有2枚反艦導彈成功突防帶有2座防空火炮的軍艦近程防御時（大于90%即可認為成功突防），突防防空火炮剛開始時，需有導彈枚數見表1。

表1 突防防空火炮之初需要導彈枚數

4 結束語

基于Markov 理論反艦導彈突防防空火炮效能評估模型，能夠動態地評估不同海況等級條件下，齊射m枚反艦導彈突防軍艦n座防空火炮的效能，這對于在攻擊水面艦艇作戰中，如何根據海況等級不同、艦艇上防空火炮座數不同而采取發射不同型號的導彈枚數用于突防防空火炮的需求具有現實的指導意義。

[1]徐浩軍,魏賢智,華玉光,等.作戰航空綜合體及其效能[M].北京:國防工業出版社,2006:2-17.

[2]ПОПОВ И С.Основы моделирования и системный анализ эффективности авиационных комплексов[M].Москва ВВИА,2002:5-15.

[3]岳奎志,韓維,王慶官.基于排隊論的機群出動能力模型[J].海軍航空工程學院學報,2009,24(2):224-228.

[4]王斯福,吳曉華,張克,等.基于排隊論的飛行器協同突防效能分析[J].戰術導彈技術,2007(1):10-15.

[5]許誠,孫永勝,孫錦.基于Markov 過程的反艦導彈突防艦艇編隊能力評估[J].飛行力學,2009,27(2):93-96.

[6]岳奎志,侯志強,韓維,等.機群出動能力的Markov模型[J].系統仿真學報,2008,20(22):6278-6282.

[7]中國船舶重工集團公司.海軍武器裝備與海戰場環境概論[M].北京:海洋出版社,2007:467-468.