基于AM-MCMC算法和Nash模型的概率洪水預報*

邢貞相 芮孝芳 馮 杰

(東北農業大學水利與建筑學院1) 哈爾濱 150030)

(東北農業大學農業工程博士后科研流動站2) 哈爾濱 150030)

(河海大學水文水資源學院3) 南京 210098)

BFS(貝葉斯概率預報系統)是一個可與任一確定性水文模型協作進行概率水文預報的通用理論框架[1],其理論基礎是貝葉斯公式.Krzysztofowicz相繼提出了線性正態假設、亞高斯轉換、概率定量降雨預報和概率河流水位預報的貝葉斯系統等[2],推動了BFS的研究進展.國內,張洪剛采用平穩序列線性AR模型與線性擾動模型(LPM)分別描述先驗分布與似然函數,在一定程序上降低了貝葉斯求解的復雜度[3];李向陽等采用神經網絡模型來描述先驗分布與似然函數,進一步降低了貝葉斯求解過程的復雜程度[4].王建平等[5]將貝葉斯理論用于水質模型的參數識別問題,對復雜環境模型參數的不確定性進行了研究.貝葉斯理論還是貝葉斯網絡模型的基礎,它是一種不確定性知識的表達與推理模型,在建筑、經濟,環境等領域均有廣泛應用[6].本文嘗試將貝葉斯理論與自適應馬爾可夫鏈蒙特卡羅算法相結合來研究Nash模型參數的不確定性,并將其用于洪水概率預報.

1 BFS的基本原理

BFS的理論依據就是下列貝葉斯公式

式中:π(θ|x)為參數的后驗密度,它是在樣本 x給定條件下,參數 θ的條件分布;π(θ)為θ的先驗分布;p(x|θ)為似然函數;Θ為θ的積分區間.

π(θ|x)集中了總體、樣本和先驗等3種信息中有關θ的信息,是排除一切與θ無關的信息后所得的結果.基于后驗分布 π(θ|x)對 θ進行統計推斷將更為有效、合理,稱之為貝葉斯統計推斷.

當參數的先驗密度與似然函數形式確定后,為獲得式(1)的后驗密度解析式還需求得其右端分母的積分,而參數θ的積分區間只能靠實測資料估計,無法獲得其真實的區間,所以,很難求得式(1)的解析式,為此,本文采用數值解法來獲得后驗密度,即用馬爾可夫鏈蒙特卡羅隨機模擬的方法求其數值解.

作為隨機模擬方法的馬爾可夫鏈蒙特卡羅(MCMC)方法的關鍵是如何選擇推薦分布(轉移密度)使采樣更加有效.常用的采樣方法有Metropolis-Hastings算法、吉布斯(Gibbs)采樣和Adapative-Metropolis(AM)算法[7].這 3種方法中只有AM算法的不依賴于事先確定的推薦分布且可并行運算,收斂速度快,故本文采用此算法.關于AM算法的具體過程和收斂判斷準則及性能測試參見文獻[8-9].

2 Nash模型參數的不確定性

本文利用AM-MCMC算法將Nash模型參數k,n分兩種情況研究其不確定性:(1)將參數k視為隨機的,而參數n視為確定性的;(2)將2參數均視為隨機的.由于第一種情況是第二種情況的特例,故本文只介紹第二種情況的具體過程.Nash模型的輸入,即地面凈雨的計算采用斜線分割法.

選取長江三峽沿渡河流域作為研究區域,共有30場洪水實測資料.該流域位于長江三峽地區,其水系流經神農架林區巴東縣.流域內降水豐沛,流域多年平降雨量為1 337 mm,全年雨量以5～9月最多,約占全年68%.流域內最大年降水量為2 448.2 mm,最小年降雨量為808.4 mm.

沿渡河流域面積601 km2,流域坡度較大,平均坡度為0.287%,高程垂直落差達2 800 m,山高坡陡,人類活動影響較小,流域內耕地面積占流域面積的10%左右,森林覆蓋率在70%以上.由于流域內植被覆蓋良好,地表徑流中含沙量不大,除洪水期含沙量有所增大外,其余時間河水清澈.

2.1 先驗分布的確定

1)參數n的先驗分布的確定 假定其服從正態分布,根據地貌學的方法求得沿渡河流域的Nash模型參數n=3,可認為是其分布的均值,設其先驗方差為均值的10%,則得n的先驗分布為n～N(3,0.3).

2)參數k先驗分布的確定 首先率定參數 ,選用該流域1981～1987年間28場洪水資料來率定參數k值.為保證計算精度,取計算時段長為1 h.為避免異參同效現象的影響,令n=3保持不變,單獨率定k,方法采用矩法-優選法.根據各場洪水k的率定結果求得k取值范圍為[1,1.96],其均值為1.19,方差為0.09,并假定其服從正態分布,即得k的先驗分布為k～N(1.19,0.09).

2.2 似然函數的確定

由于有28場洪水資料參與率定,故采用多觀測擬合優度的似然函數

式中:Q為流量;σei為第i個觀測與模型預報的誤差系列的標準差;N為實測序列的個數,本文為N=28;其余符號意義同前.

2.3 AM-MCMC算法初始條件

AM-MCMC算法初始條件:初始協方差取為對角陣,初始化迭代次數為2 000,初始化階段次數為2 000,每次采樣為10 000次,算法并行運行5次,這樣共將取樣(10 000-2 000)×5=40 000組(n,k)以用于沿渡河流域Nash模型參數的不確定性研究.

2.4 Nash模型參數不確定性分析

AM-MCMC運算結束后,根據所抽40 000個樣本,統計得出Nash模型參數的邊緣后驗密度分別為 k～N(2.03,0.09)(見圖 1),n～N(2.61,0.10)(見圖2),從圖1,圖2可見k和n的后驗邊緣密度均近似服從正態分布,通過Kolmogorov-Smirnov假設檢驗在顯著性水平為0.05時接受各自后驗分布為正態分布的原假設.圖3給出了2參數的后驗均值迭代跡線、圖4給出了2參數的后驗方差迭代跡線,從2圖中看出自第2 000次迭代后2參數的后驗均值、后驗方差均趨于穩定,說明所抽樣本已具有總體樣本的統計特性.圖5給出了兩參數的聯合后驗概率密度,從圖中看出兩參數的聯合分布只有一個極值,其坐標為兩參數的后驗均值.圖6給出了兩參數樣本的散點圖,由圖可見,n與k之間存在著明顯的相關關系.

圖1 參數k的后驗邊緣密度

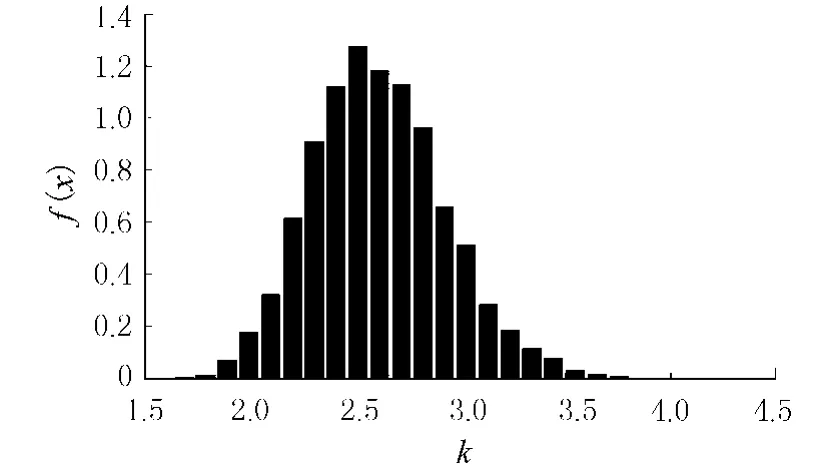
圖2 參數n的后驗邊緣密度

圖3 參數n,k的后驗均值迭代跡線

圖6 參數n與k的散點圖

3 Nash模型的降雨徑流概率預報

芮孝芳[10]指出,產生水文模型的“異參同效”這一現象的原因至少有:目標函數是多極值的;模型中包含的參數之間存在相互補償作用;模型參數具有隨機性.圖1和圖2雖給出了Nash模型兩參數的各自后驗邊緣密度,但卻無法避免存在的“異參同效”現象,在實際水文預報時,真正有意義的是兩個參數的組合,而不是單個參數.為此,本文隨機選取AM-MCMC算法收斂后的10 000個參數組樣本分別對沿渡流域洪水進行模擬,使某一場洪水的每個時段對應所選取的不同參數組生成10 000個流量數值.用這些數據作為樣本來研究各時刻流量的統計特性,即可求得各時刻(包括洪峰時刻)流量的概率分布,其均值和方差及指定概率的置信區間.在作業預報時可采用每一時刻的預報流量樣本的均值作為其預報值.

表1中只給出了本文算法對沿渡河流域6場洪水(其他洪水限于篇幅未列出)的峰值概率預報及其80%的置信區間.在表1中,同時給出了當參數k為隨機而n為確定時的相應場次洪水的峰值預報結果(研究方案1為僅參數k為隨機的情況,方案2為參數k和n均為隨機的情況).通過對該流域30(其中的28場為參數率定過程所用過的洪水作為校核樣本,另810824和870827兩場為預報樣本)場洪水的預報結果可知,其中洪峰預報誤差在20%以內的場次占總體的77%,洪峰誤差小于10%的場次占總體的60%.平均洪峰誤差為12.6%,所有洪峰滯時均在3 h以內,平均洪峰滯時為1.3,所有確定性系數均大于0.70,平均確定性系數為0.86;與單一參數k為隨機的模型預報結果相比,大部分洪水的洪峰誤差有所降低,確定性系數稍有提高;平均確定性系數相當,而平均洪峰滯時降低了58%.這說明了Nash模型的確存在著較強的“異參同效”現象.兩場預報洪水的計算精度也較高.與僅k為隨機的情況下的預報結果相比,2參數均為隨機的計算洪峰均方差和80%的置信區間均有所增大,這說明預報結果的不確定性增大了,這也正是由于增加了參數n的不確定性所致.綜述之,模型參數的不確定性對確定性系數影響較小,對洪峰誤差、洪峰滯時和置信區間影響較大.

圖7繪出了洪號為810714 a)和810824 b)2場洪水的洪峰后驗密度直方圖及其極大似然估計的理論正態密度曲線,據圖看出各洪峰的密度直方圖與估計的理論正態密度曲線吻合較好.圖8繪出了這2場洪水的80%的置信區間與實測洪水的比較,據圖看出每場洪水的實測流量幾乎都包括在80%的置信區間內.圖9給出了這2場洪水基于AM-MCMC算法的Nash模型2參數均為隨機的BFS預報均值過程與實測過程的比較.由圖9可見,2場洪水的擬合精度都很高.

表1 沿渡河流域參數隨機的Nash模型的概率洪水預報成果表

圖7 洪峰后驗密度直方圖及其理論密度曲線

圖8 概率預報的80%置信區間與實測過程比較

圖9 概率預報過程與實測過程比較

4 結 論

1)貝葉斯概率預報系統可與任一復雜的確定性水文模型協同工作,而無需附加任何假設,是制定概率水文預報的通用理論框架.

2)AM算法采用并行抽樣,速度快,無需事先指定MCMC算法的推薦分布,且考慮所抽歷史樣本的信息,能準確地獲得指定參數的總體分布特征,具有算法上的優越性.

3)AM-MCMC算法能較好獲取Nash模型參數k,n的后驗分布特征,Nash模型的兩個參數均存在較強的不確定性,沿渡河流域兩參數均近似服從正態分布.使模型的應用不再受有限實測資料的制約.

4)貝葉斯概率洪水預報不僅可給出洪水各時刻的流量,而且能借助給出的各時刻的流量方差考慮洪水預報的不確定性,便于在實際應用中估計各種防洪決策的風險.

[1]Krzysztofowicz R.Bayesian theory of probabilistic via deterministic hydrologic model[J],Water Resour.Res.,1999,35(9):2 739-2 750.

[2]Krzysztofowicz R,Maranzano C J.Hydrologci uncertainty processor for probabilistic stage transition forecasting[J].Journal of Hydrology,2004,293(1-4):57-73.

[3]張洪剛.貝葉斯概率水文預報系統及其應用研究[D].武漢:武漢大學水利水電學院,2006.

[4]李向陽,程春田,林劍藝.基于BP網絡的貝葉斯概率水文預報模型[J].水利學報,2006,37(3):354-359.

[5]王建平,程聲通,賈海峰.基于MCMC法的水質模型參數不確定性研究[J].環境科學,2006,27(1):24-30.

[6]陳小佳,沈成武.既有橋梁的貝葉斯網絡評估方法.武漢理工大學學報:交通科學與工程版,2006,30(1):132-135.

[7]Haario H,Saksman E,Tamminen J.An adaptive metropolis algorithm[J].Bernoulli,2001,7(2):223-242.

[8]Gelman A,Carlin J B,Stren H S,et al.Bayesian data analysis[M].London:Chapmann and Hall,1995.

[9]Gelman A,Rubin D B.Inference from iterative simulation using multiple sequences[J].Statistics Science,1992,7(4):457-511.