一種改進型B樣條的曲線參數化方法

付麗輝

FU Li-hui

（江蘇省淮陰工學院 電子與電氣工程學院，淮安 223003）

一種改進型B樣條的曲線參數化方法

A improved re-parameterization method in b-spline curves

付麗輝

FU Li-hui

（江蘇省淮陰工學院 電子與電氣工程學院，淮安 223003）

提出了β參數型-B樣條曲線的重新參數化方法。通過構建新的參數可控的基函數，實現對B樣條基函數的重新參數化，進而實現了對曲線的重新參數化，并通過MATLAB軟件建立實驗平臺。實驗結果表明，只要β參數選擇合適，新的方法完全可以達到與傳統方法同樣的效果，但新算法增加了更加靈活的控制內容，可以根據實際要求實現對曲線的重新擬合，使得算法的靈活性大大提高，且計算簡單，具有良好的通用性。

MATLAB仿真；B樣條函數；重新參數化；曲線

0 引言

60年代末70年代初，人們在Bezier方法的基礎上開始注意B樣條理論在自由曲線曲面造型中的應用，最初的成果包括Riesenfeld[1]，Coons[2]和Clark[3]等研究者的著作，之后的10年間，各國學者先后對B樣條方法進行了更為廣泛的實用研究，如Greenberg[4]和Judd[5]等人所發(fā)表的論文、著作所述。B樣條曲線的應用范圍非常廣泛，不僅可用在幾何造型方面，還可以用于處理力學、圖像、數據壓縮等問題。隨著B樣條曲線的不斷改進，其研究、應用推廣的價值在不斷提高。

本文在B樣條曲線基本理論的基礎之上，討論了如何尋找更廣泛意義的基函數以及參數變換，通過構建基于 參數的改進的基函數，實現對基函數的重新參數化，從而實現對B樣條曲線的重新參數化，并以三次均勻B樣條曲線為例說明了該種方法的可行性。由仿真結果可知，該方法可以在自由曲線和曲面的構建中達到更加靈活的控制效果。

1 參數型-B樣條基函數

在對曲線重新參數化的過程中，可以考慮先對一般的B樣條函數進行參數變換，尋找具有更廣意義的基函數，并以此作為切入點，從而實現對曲線的重新參數化。下面以三次均勻B樣條基函數為例說明這種函數的建立過程。

1）式所表示的基函數分屬于四條B樣條，但處于相同的節(jié)點區(qū)間內，因它們都是均勻的B樣條，故可以將其拼接成一條完整的B 樣條[6]，如圖1所示。

圖1 三次均勻B樣條基函數

為實現重新參數化，現構建以下基函數：

其中，u=at(1-t)，在該表達式中，a=4，t為[0,1]間的隨機數，表達式u=at(1-t)可以看作是非線性的映射模型，屬于混沌動力學模型，當a=4時，其混沌解將布滿整個[0,1]區(qū)間，即在[0,1]區(qū)間上是遍歷的。

將g(u)代替三次B樣條基函數中的參數，可以得到：

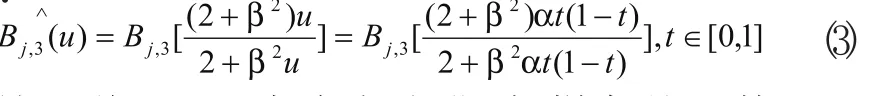
這里將（3）式稱為改進型B樣條基函數，記為β參數型-B樣條基函數，利用該函數可以將常規(guī)的B樣條基函數進行推廣。分析（3）式可知：當β=0時，這就是說，β參數型-B樣條基函數是常規(guī)B樣條基函數的推廣形式，只要變化參數β，即可得到各種B樣條基函數，從而可以實現對曲線的重新參數化。

根據以上的算法，下面針對三次均勻B樣條基函數進行變換，可以得到其對應的具體 參數型-B樣條基函數的表達式為：

當β=1時，該函數則為：

由MATLAB仿真程序可以得到三次均勻B樣條基函數以及其對應的重新參數化的β參數型-B樣條基函數圖形，如圖2所示：

圖2 三次均勻B樣條與β參數型-B樣條基函數

2 β參數型-B樣條曲線及其性質

2.1 β參數型-B樣條曲線

下面仍以三次均勻B樣條基函數為例說明這種曲線的建立過程。首先給出三次均勻B樣條曲線的矩陣[7]表示。

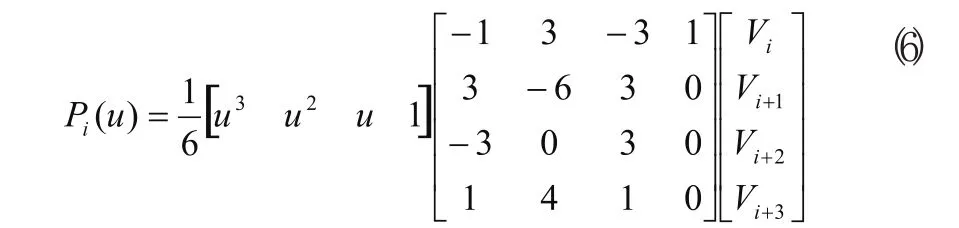
而本文所述的β參數型-B樣條基函數所對應的曲線則表示為：

當β=1時，對應曲線可以表現為（8）式：

經比較可以發(fā)現，兩種曲線參數化方法非常相似，只要令參數β=0，兩者完全相同，所不同之處在于三次β參數型-B樣條基函數所對應的曲線是三次均勻B樣條曲線的特例，如果變換其β參數的值，可以得到無數多種與三次均勻B樣條曲線相類似的表達式，由此可以為不同情況下的曲線重新參數化打下良好的基礎。接下來一節(jié)將研究一下β參數型-B樣條曲線所具有的主要特性，從而進一步來說明該方法的實質。

2.2 β參數型-B樣條曲線的主要性質

1）不同β參數的樣條曲線上的點與參數域的點對應關系不同

證明：由上可知，當i=0時，B樣條基函數曲線的表達式為：

而β參數型-B樣條曲線的表達式為：

根據(13)式可知：當u取固定參數u0時，曲線上某點坐標與β相關，隨β變化而變化，因此，不同β參數的樣條曲線上的點與參數域的點對應關系不同。

2）變換前后，各個β參數的樣條曲線的一階導矢的方向互相平行，但模長發(fā)生變化

至于其他類似于常規(guī)B樣條曲線的性質，諸如局部性、可微性、參數連續(xù)性等就不再一一證明。

根據以上證明可知：β參數型-B樣條曲線方法提供了多種曲線的生成方式，對于一條K次B樣條曲線，只要改變參數β，即可在不改變曲線形狀的條件下實現對曲線的重新參數化，從而使得曲線上的點與參數域內的點的對應關系發(fā)生相應變化。

3 仿真過程及結果

本節(jié)將通過仿真的方法來驗證該算法的可行性。利用MATLAB軟件編寫仿真程序，構建基于同一組數據點的控制多邊形的三次B樣條曲線與其對應的β參數型-B樣條曲線，其中控制多邊形由以下控制點來決定：[4 6]，[3 5]，[2 4]，[3 2]，[6 1]，[5 8]，[10 6]，[8 1]，[6 0]，[4 -1]，下面給出參數型-B樣條曲線仿真程序的主要部分。

a=[4 3 2 3 6 5 10 8 6 4;6 5 4 2 1 8 6 1 0 -1];%控制點

subplot(2,2,2)

plot(a(1,:),a(2,:),':'); % 繪制控制多邊形；

hold on; %

xlabel('(b)改進樣條算法')

for i=1:7;

for t=0:0.001:1;

u=(2+1).*t/(2+1.*t)% β參數型-B樣條曲線的核心算法，其中β=1；

b0=1.0./6.*(1-u).^3; % 基函數b0；

b1=1.0./6.*(3.*u.^3-6.*u.^2+4); % 基函數b1；

b2=1.0./6.*(-3.*u.^3+3.*u.^2+3.*u+1); % 基函數b2；

b3=1.0./6.*u.^3; % 基函數b3；

x=b0.*a(1,i)+b1.*a(1,i+1)+b2.*a(1,i+2)+b3.*a(1,i+3); % 確定曲線的橫坐標x；

y=b0.*a(2,i)+b1.*a(2,i+1)+b2.*a(2,i+2)+b3.*a(2,i+3); % 確定曲線的縱坐標y；

line(x,y); % 繪制曲線坐標點；

end

end

hold off;

最后可以得到如圖3的仿真結果。

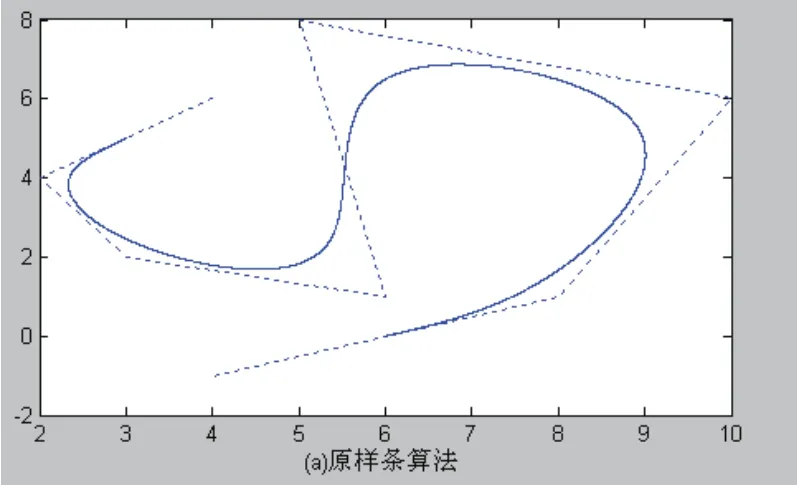
圖3 三次B樣條曲線與β參數型-B樣條曲線

圖3中的虛線所示為控制多邊形，實線則為兩種方法生成的曲線。其中，(a)圖為三次B樣條曲線，(b)圖為β參數型-B樣條曲線，對應β=1，至于β取其他不同參數的曲線，這里就不再一一給出。由仿真結果可知：當β參數選擇合適時，新方法完全可以達到與傳統方法同樣的效果，但新算法增加了更加靈活的控制內容，可以根據實際要求實現對曲線的重新參數化，這主要體現在：一方面，在繪制曲線時，如果已知曲線的某些點的期望值，在實際曲線點與期望值不符的情況下，可以根據已知信息計算參數β值，從而對曲線進行重新參數化，以達到給定要求；另一方面，若繪制的圖形有多條，且存在交點，在這種情況下，如果利用常規(guī)的B樣條曲線進行擬合時，其交點的參數μ是不同，但是，如果利用β參數型-B樣條方法，效果則不同，可先給出其中的一條曲線的β參數型-B樣條曲線的形式，再由參數化條件確定的具體值，從而將該曲線進行重新參數化，以達到交點處的兩條曲線的參數μ相同的目的。

4 結論

本文給出了β參數型-B樣條曲線的重新參數化方法，通過改變參數β的具體取值以實現對基函數的重新參數化，進而實現對曲線的重新參數化。該方法使得B樣條曲線的擬合算法的靈活性大大提高，且其計算簡單，具有良好的通用性。另外，本文主要以三次均勻B樣條基函數為例來說明方法的有效性，但這種β參數型-B樣條曲線的重新參數化還可以很方便地用于其他類型的樣條基函數中，并且，也能推廣到其他曲線和曲面的表示法中，具有一定的實用及研究意義。

[1] Riesenfeld,R.F.,Applications of B-Spline Approximation to Geometric Problems of CAD,ph.D Thesis,Syracuse University,1973.

[2] Coons.S.A.,Surface Patches and B-Spline Curves,in Computer Aided Geometric Design,R.E.Barnhill and R.F.Riesenfeld,Editors,Academic Press,1974.

[3] Clark,J.H.,3-D Design of Free-Form B-Spline Surfaces,Ph.D Thesis,University of Utah,Salt Lake City,Utah,Sept.1974.

[4] Wu,S-C.,Abel,J.f.and Greenberg D.P.,An Interactive Comp uter Graphics Approach to Surface Representation,Communications of the ACM,1977,20(10).

[5] Hartley,P.J.and Judd,C.J.,Parametrization of Bezier-Type B-Spline Curves and Surfaces,CAD,1978,10(2).

[6] 朱心雄.等.自由曲線曲面造型技術[M].科學出版社,2000.

[7] 施法中.計算機輔助幾何設計與非均勻有理B樣條[M].高等教育出版社,2001.

TP273

A

1009-0134(2010)12(上)-0133-04

10.3969/j.issn.1009-0134.2010.12(上).44

2010-08-06

江蘇省科技支撐項目（BE2009100）

付麗輝（1975 -），女，講師，碩士研究生，研究方向為模式識別與智能控制。