基于有向圖的二維約束求解算法研究

王世平， 郭連水

（北京航空航天大學(xué)機(jī)械工程及自動(dòng)化學(xué)院，北京 100191）

基于有向圖的二維約束求解算法研究

王世平， 郭連水

（北京航空航天大學(xué)機(jī)械工程及自動(dòng)化學(xué)院，北京 100191）

針對(duì)過(guò)約束、幾何完全定義狀態(tài)判定和約束求解效率等問(wèn)題，提出了基于約束圖，利用自由度理論和約束沖突機(jī)制，通過(guò)反向約束方向平衡約束，進(jìn)而通過(guò)排序進(jìn)行約束求解的算法。算法采用約束圖記錄約束和幾何的關(guān)系；通過(guò)約束平衡的方法進(jìn)行過(guò)約束和幾何完全定義的判定；采用排序求解方法，將龐大計(jì)算問(wèn)題轉(zhuǎn)化為一組相對(duì)簡(jiǎn)單的計(jì)算問(wèn)題。算法已得到初步應(yīng)用，對(duì)過(guò)約束和幾何完全定義狀態(tài)的判定有明顯的效果，而且提高了約束求解效率。

計(jì)算機(jī)應(yīng)用；幾何約束求解；約束圖；過(guò)約束；完全定義；排序求解

約束求解是CAD變量化系統(tǒng)草圖設(shè)計(jì)的重要組成部分，用以滿足快速交互設(shè)計(jì)的需要。國(guó)內(nèi)外學(xué)者進(jìn)行了大量的研究，主要方法有基于數(shù)值求解、基于符號(hào)求解、基于規(guī)則求解和基于圖論求解[1]。其中基于圖論的求解方法[2-6]最為直觀、嚴(yán)謹(jǐn)，而且可以方便地進(jìn)行過(guò)約束和幾何完全定義狀態(tài)的判斷。

J Y Lee和K Kim提出的全約束下的圖論和數(shù)值相結(jié)合的方法[1]是目前應(yīng)用最廣泛的方法之一。趙萬(wàn)生等提出的局部影響域算法[3]給出了一種應(yīng)用圖論解決欠約束問(wèn)題的方法。董金祥等提出的基于圖論的拓?fù)渑判蚍椒╗4]不但適用于欠約束情況，而且也能處理較簡(jiǎn)單的過(guò)約束問(wèn)題。目前的文獻(xiàn)對(duì)簡(jiǎn)單的過(guò)約束問(wèn)題（剩余自由度小于零）有一定的探討，但對(duì)于相對(duì)復(fù)雜的過(guò)約束和對(duì)幾何完全定義狀態(tài)的確定卻少有涉及。

本文從變量化造型系統(tǒng)應(yīng)用出發(fā)，重點(diǎn)討論約束信息的管理、過(guò)約束和幾何完全定義狀態(tài)的判定、排序求解方法等，建立了二維約束求解算法：記錄約束圖約束和幾何的關(guān)系，作為約束求解的基礎(chǔ)；調(diào)整約束圖平衡約束，判定過(guò)約束和幾何完全定義狀態(tài)；以調(diào)整后的約束圖為基礎(chǔ)，將需要計(jì)算的幾何元素進(jìn)行排序，高效完成方程組求解。

1 約束模型表示方法

在進(jìn)行復(fù)雜草圖設(shè)計(jì)時(shí)，常常面臨約束關(guān)系管理的問(wèn)題。本文采用約束圖表達(dá)約束模型，圖的頂點(diǎn)表示幾何元素，邊表示約束。約束圖將相互關(guān)聯(lián)的所有幾何和約束聯(lián)系在一起。

1.1 頂點(diǎn)

頂點(diǎn) 表示某一幾何元素，如點(diǎn)、直線、圓等。

頂點(diǎn)分為前承頂點(diǎn)和傳遞頂點(diǎn)兩種。兩類頂點(diǎn)是相對(duì)于約束邊來(lái)區(qū)分的。如圖1(a)，約束e1箭頭指向的頂點(diǎn)L1稱為e1的傳遞頂點(diǎn)，約束e1箭頭起始的頂點(diǎn)P1稱為e1的前承頂點(diǎn)。

1.2 約束邊

約束邊 用帶箭頭的約束邊（有方向的邊）來(lái)表示某一約束。

約束邊分為前承約束和傳遞約束兩種。兩類約束是相對(duì)頂點(diǎn)來(lái)區(qū)分的。如圖1(a)，指向頂點(diǎn)L1的約束邊e1稱為L(zhǎng)1的前承約束，從頂點(diǎn)L1起始的約束邊e2稱為L(zhǎng)1的傳遞約束。

1.3 約束圖建立方法

約束圖 由頂點(diǎn)和約束邊組成的圖形，稱為約束圖。

約束圖的建立過(guò)程就是創(chuàng)建新的頂點(diǎn)和約束邊，并將它們聯(lián)系在一起的過(guò)程。

示例如圖1所示。

建立由3個(gè)點(diǎn)P1、P2、P3和3條直線L1、L2、L3組成的三角形，如圖1(a)所示。在約束圖中創(chuàng)建6個(gè)幾何元素的頂點(diǎn)P1、P2、P3、L1、L2、L3；之后創(chuàng)建6個(gè)點(diǎn)在直線上的約束e1～e6；建立這6條約束邊與頂點(diǎn)之間的關(guān)系：e1是P1與L1之間的約束（e1由P1指向L1），e2～e6類似處理，如圖1(b)所示。

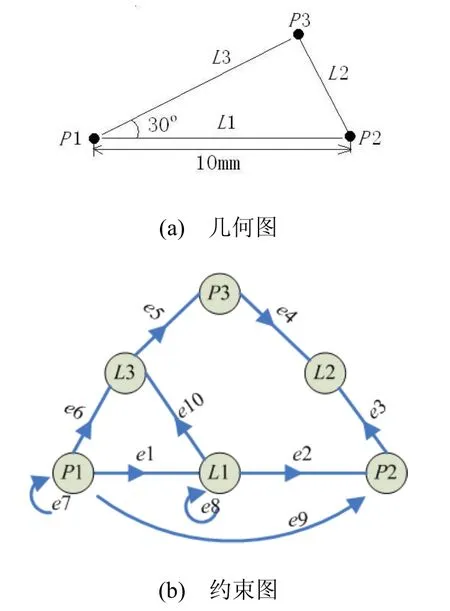
圖1 幾何圖和約束圖

新添加兩點(diǎn)P1與P2間10mm的距離約束e9。首先在約束圖中創(chuàng)建約束邊e9，之后建立約束邊e9與頂點(diǎn)P1與P2的關(guān)系（e9由P1指向P2）。新添加點(diǎn)P1的固定約束e7、直線L1的水平約束e8、兩直線L1與L3間的30o角度約束e10。

約束是有向的。不同的約束方向表示不同的約束方式和計(jì)算方式。如圖 1(b)，距離約束 e9是由P1指向P2的，這表示點(diǎn)P1通過(guò)10mm的距離來(lái)約束點(diǎn)P2；在計(jì)算P2時(shí)，可以通過(guò)P1的位置和10mm的距離約束e9來(lái)求解P2的位置。

在約束圖的建立過(guò)程中，約束方向的確定將影響約束求解過(guò)程。本文是先任意選取一個(gè)方向，再通過(guò)下文約束平衡方法來(lái)修改約束的方向，避免因約束方向不當(dāng)而引起幾何的過(guò)定義。

2 基于約束圖的約束平衡方法

通過(guò)約束圖的調(diào)整（修改約束的方向）平衡約束關(guān)系，無(wú)法平衡的約束則為過(guò)約束。在約束求解方程組計(jì)算之前平衡約束關(guān)系，能夠避免幾何過(guò)定義導(dǎo)致的無(wú)解方程組計(jì)算，提高求解效率。

2.1 過(guò)約束的概念

幾何過(guò)定義 由于幾何的約束冗余導(dǎo)致約束求解失敗，稱其為幾何過(guò)定義。

過(guò)約束 導(dǎo)致約束圖存在過(guò)定義幾何的約束稱為過(guò)約束。

導(dǎo)致幾何過(guò)定義的原因主要有 2個(gè)：① 幾何的剩余自由度小于零；② 約束沖突。前者是由于約束過(guò)多，后者是由于約束彼此相矛盾造成了幾何的無(wú)解。

剩余自由度 某幾何的自由度減去其前承約束的約束度之和，其差值稱為該幾何的剩余自由度。

RDOF(P)= DOF(P)-∑DOC(ei) （1）例如，如圖 1中，直線 L1的剩余自由度RDOF(L1)= DOF(L1)-∑DOC(ei)=2-1-1=0。

約束沖突 多個(gè)約束相互矛盾而導(dǎo)致約束求解失敗，稱其為約束沖突。

約束沖突舉例：如圖1(b)約束圖，若反向角度約束e10，則角度約束e10與水平約束e8產(chǎn)生約束沖突。在計(jì)算直線 L1時(shí)，其方向或水平，或與L3成30°角，二者選其一。約束e10與e8彼此矛盾，不能同時(shí)指向同一個(gè)幾何。

2.2 約束平衡方法

從幾何過(guò)定義的概念知道，過(guò)定義的出現(xiàn)實(shí)際上是由于幾何的約束負(fù)擔(dān)（前承約束）過(guò)重。為了避免幾何過(guò)定義，需要進(jìn)行約束平衡，即減少過(guò)定義頂點(diǎn)的前承約束。

修改約束方向后，該約束新指向的幾何有可能會(huì)由原來(lái)的非過(guò)定義狀態(tài)轉(zhuǎn)變?yōu)檫^(guò)定義狀態(tài)。那么，如何選擇合適的前承約束進(jìn)行反向以及反向約束后產(chǎn)生新的過(guò)定義幾何時(shí)的處理方法就成為算法的關(guān)鍵。算法主要步驟如下：

Step 1 找到過(guò)定義頂點(diǎn)P0（剩余自由度小于0的頂點(diǎn)或相沖突的約束的傳遞頂點(diǎn)）。

Step 2 在P0的前承約束中挑選一個(gè)約束e進(jìn)行反向，要求反向e后P0不再是過(guò)定義頂點(diǎn)。反向約束e后進(jìn)入下一步Step 3。若沒(méi)有合適的前承約束可以反向，分下列兩種情況：若P0是因?yàn)榉聪蚣s束 e0導(dǎo)致的過(guò)定義頂點(diǎn)，那么恢復(fù)e0的方向，重新選擇一個(gè)合適的前承約束反向（即返回上一個(gè)訪問(wèn)頂點(diǎn)轉(zhuǎn)Step 2）。若P0是最初的那個(gè)過(guò)定義頂點(diǎn)，那么，算法結(jié)束，該約束圖存在過(guò)約束，約束平衡失敗。

Step 3 被反向的約束e的傳遞頂點(diǎn)P1，若P1不是過(guò)定義頂點(diǎn)，則約束圖調(diào)整成功（約束平衡成功），約束圖不存在過(guò)約束；若P1是過(guò)定義頂點(diǎn)，將P1當(dāng)作P0，轉(zhuǎn)Step 2。

示例 在圖1(a)幾何圖中，新添加L2與L1的垂直約束 e11，如圖 2(a)。過(guò)定義頂點(diǎn)可能是新添加約束e11的傳遞頂點(diǎn)L1。

如圖 2(a)，L1是過(guò)定義頂點(diǎn)，其前承約束e11和e8約束沖突，且L1的剩余自由度小于0。由于存在約束沖突，只能反向e8或e11（反向其他前承約束無(wú)法解除L1的過(guò)定義狀態(tài)）。反向e8后L1仍是過(guò)定義狀態(tài)，恢復(fù)e8的方向（反向e8失敗）；反向約束e11，使L1不再是過(guò)定義頂點(diǎn)，如圖2(b)所示。

反向e11后，e11的傳遞頂點(diǎn)L2變?yōu)檫^(guò)定義頂點(diǎn)，其剩余自由度小于0。反向L2的前承約束e3，使L2不再是過(guò)定義頂點(diǎn)，如圖2(c)所示。

反向e3后，e3的傳遞頂點(diǎn)P2變?yōu)檫^(guò)定義頂點(diǎn)，其剩余自由度小于 0。反向 P2的前承約束e9，使P2不再是過(guò)定義頂點(diǎn)，如圖2(d)所示。

反向e9后，e9的傳遞頂點(diǎn)P1變?yōu)檫^(guò)定義頂點(diǎn)。P1沒(méi)有合適的前承約束可以反向，恢復(fù) e9的方向，如圖2(c)所示。

重新選擇P2的一個(gè)前承約束e2進(jìn)行反向，使P2不再是過(guò)定義頂點(diǎn)，如圖2(e)所示。按照之前的分析方法可得反向e2失敗，恢復(fù)e2的方向，如圖2(c)所示。

P2沒(méi)有合適的前承約束可以反向，恢復(fù)e3的方向，如圖2(b)所示。

重新選擇L2的一個(gè)前承約束e4進(jìn)行反向，使L2不再是過(guò)定義頂點(diǎn)，如圖2(f)所示。

反向e4后，e4的傳遞頂點(diǎn)P3不是過(guò)定義頂點(diǎn)，約束圖調(diào)整成功（約束平衡成功）。

由上例可以看出，約束平衡是由新添加或修改的約束為起始的。實(shí)際上，每次添加或修改新的約束時(shí)，都要進(jìn)行約束平衡。如此，下次新添加或修改約束就是在平衡約束圖基礎(chǔ)上的操作，只需要考慮新的約束帶來(lái)的影響即可。

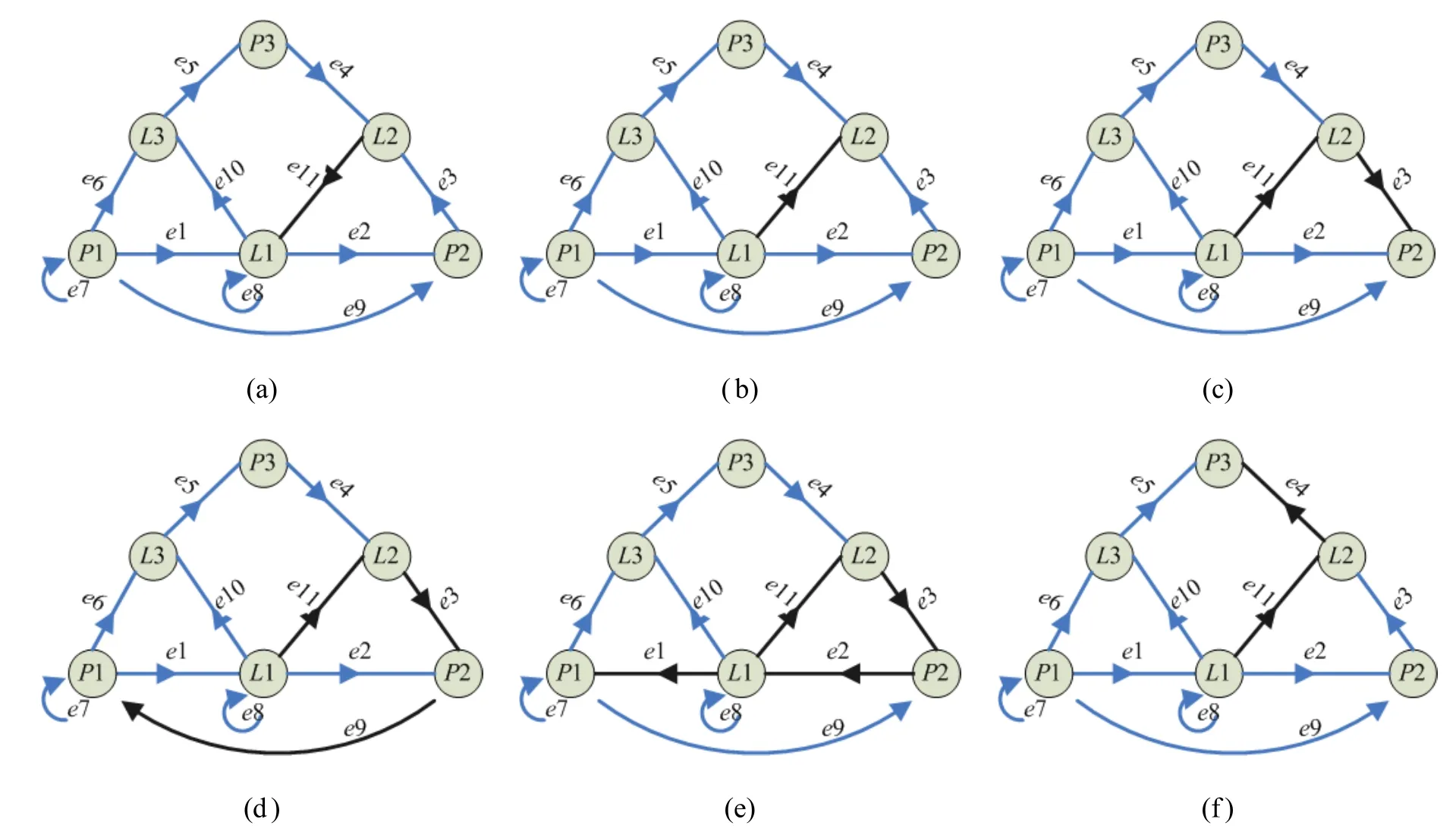
圖2 約束平衡方法示意圖

2.3 過(guò)約束判斷

過(guò)約束判斷問(wèn)題不僅需要判斷出過(guò)約束是否存在，還要判斷出過(guò)約束的幾何對(duì)象和過(guò)約束的位置。過(guò)約束判斷規(guī)則如下：

規(guī)則1 約束平衡失敗，則存在過(guò)約束；否則不存在過(guò)約束。

規(guī)則2 約束平衡失敗后，約束圖中所有反向失敗的約束都是過(guò)約束。

規(guī)則3 過(guò)約束指向的幾何就是過(guò)約束所在的幾何。

由于約束沖突的判斷機(jī)制，上述規(guī)則可以判斷出許多特殊的過(guò)約束。

示例 如圖3的幾何圖和約束圖，e1～e4是點(diǎn)在直線上約束；e5是直線L1的水平約束；e6是直線L2的豎直約束；e7是圓C1與直線L2的相切約束。新添加L1和L2的平行約束e8。按照算法進(jìn)行約束平衡，如圖3(b)，結(jié)果是約束平衡失敗，判定約束圖存在過(guò)約束；約束圖中e5、e6和 e8反向失敗（由于約束沖突的機(jī)制，其他約束沒(méi)有被反向），判定為過(guò)約束；它們所指向的幾何L1和L2為過(guò)約束所在幾何。即水平、豎直和平行約束為過(guò)約束，直線L1和L2為過(guò)約束所在的幾何。（而相切約束等則不是過(guò)約束，圓等也不是過(guò)約束所在幾何。）

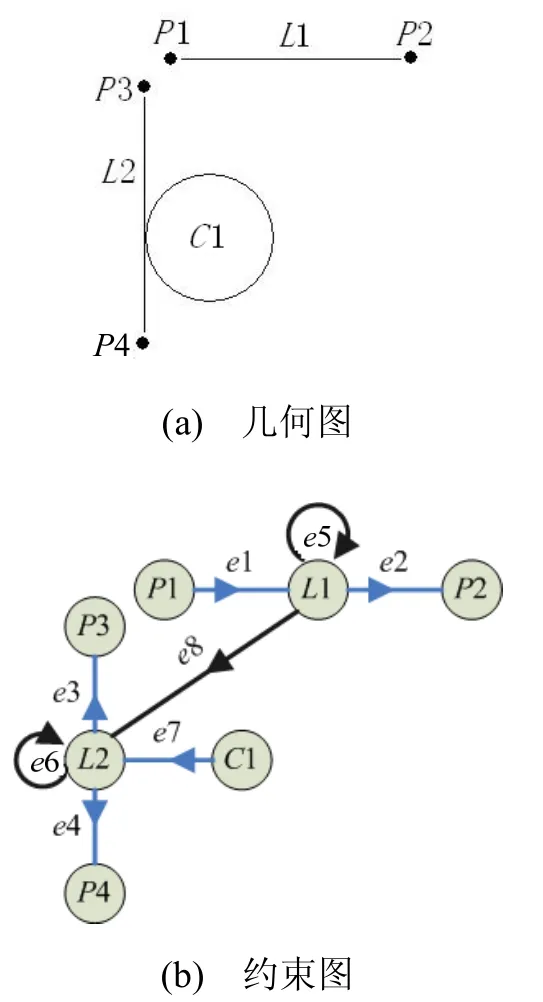
圖3 過(guò)約束判斷示意圖

2.4 幾何完全定義狀態(tài)分析方法

幾何完全定義狀態(tài)的判定有利于提高系統(tǒng)的交互設(shè)計(jì)。設(shè)計(jì)者可以參考現(xiàn)有幾何的約束狀態(tài)進(jìn)行下一步的設(shè)計(jì)，避免過(guò)約束的出現(xiàn)。

完全定義狀態(tài) 幾何的形狀和位置完全確定時(shí)的狀態(tài)稱為完全定義狀態(tài)。

幾何的完全定義狀態(tài)判斷規(guī)則如下：

規(guī)則1 該幾何的前承約束中不存在過(guò)約束。

規(guī)則2 幾何的剩余自由度等于0。

規(guī)則3 在約束圖中，反向該幾何的任意一個(gè)前承約束，利用約束平衡方法，結(jié)果是反向失敗，即該幾何的所有前承約束均無(wú)法反向。

滿足以上所有條件的幾何，處于完全定義狀態(tài)。

示例 如圖4，點(diǎn)P1有固定約束e1，點(diǎn)P1與直線 L1間存在點(diǎn)在直線上約束 e2，直線 L2有水平約束e3，直線L1和L2之間存在平行約束e4。用上述規(guī)則進(jìn)行完全定義狀態(tài)的判斷：

P1的前承約束e1不是過(guò)約束，P1剩余自由度為0，e1不能反向，因此P1是完全定義狀態(tài)。

L1的前承約束e2、e4不是過(guò)約束，L1的剩余自由度為0，反向e2和e4均失敗（e3和e4互為約束沖突，同時(shí)指向L2時(shí)出現(xiàn)過(guò)定義），因此L1是完全定義狀態(tài)。

L2的前承約束e3不是過(guò)約束，但L2的剩余自由度為1，因此L2不是完全定義狀態(tài)，而處于欠定義狀態(tài)。

需要注意的是，“只有前承幾何完全定義，其傳遞幾何才可能完全定義”的觀點(diǎn)是錯(cuò)誤的。如圖4，L1的前承幾何是L2，即L1是根據(jù)L2計(jì)算出來(lái)的，而L2不是完全定義狀態(tài)，L1卻是完全定義狀態(tài)。

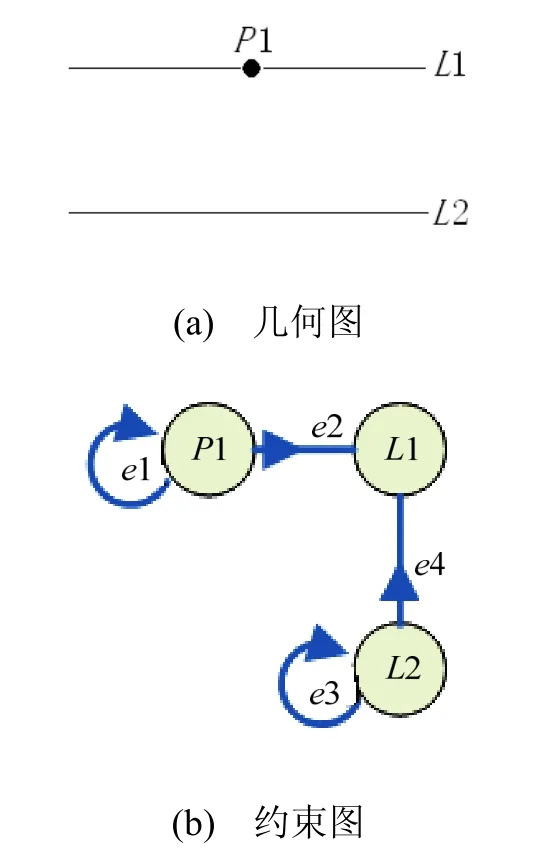
圖4 完全定義狀態(tài)判斷示意圖

3 基于約束圖的約束求解隊(duì)列算法

根據(jù)調(diào)整（約束平衡）后的約束圖，進(jìn)行求解排序，對(duì)需要求解的幾何按排序結(jié)果進(jìn)行方程組的順序求解。

3.1 基本思路

在新添加或修改約束時(shí)，求解前的幾何圖形滿足除了新約束外的所有約束，所以，只需要以新約束作為起始 ，計(jì)算新約束影響到的幾何 P以及因?yàn)閹缀蜳的改變而影響到的其他幾何。至于未影響到的幾何，作為已知幾何，不重新計(jì)算。

在重新計(jì)算幾何過(guò)程中，如果所有需要計(jì)算的幾何同時(shí)求解，計(jì)算量將會(huì)非常大。（等價(jià)于n元m次方程組。）如果將求解的幾何進(jìn)行排序，按照順序依次求解幾何，那么計(jì)算量將會(huì)大大減少。（等價(jià)于將一個(gè)大方程組拆分為若干小方程組，降低了方程組的元數(shù)。）

3.2 求解隊(duì)列算法

求解隊(duì)列算法的基本思路是：以新添加或新修改約束的傳遞頂點(diǎn)為起始點(diǎn)，沿著傳遞約束的方向，將幾何排序。排序后得到的有序隊(duì)列，就是需要重新計(jì)算的幾何元素的求解隊(duì)列。求解隊(duì)列中的每個(gè)隊(duì)列元素含有一個(gè)或多個(gè)幾何元素，同一個(gè)求解隊(duì)列元素內(nèi)的幾何元素在計(jì)算中同時(shí)求得。算法如下：

Step 1 將求解隊(duì)列Queue清空；

Step 2 得到新添加或新修改約束 e的傳遞頂點(diǎn)P0；

Setp 3 將 P0作為一個(gè)求解隊(duì)列元素壓入求解隊(duì)列Queue的隊(duì)尾；

Step 4 遍歷P0的傳遞約束。若P0的傳遞約束都遍歷完畢，則轉(zhuǎn)Step 9。否則，選中一條未遍歷的傳遞約束e1，得到e1的傳遞頂點(diǎn)P1；

Step 5 若P1不在求解隊(duì)列Queue中，則記錄P1的父頂點(diǎn)：F（P1）＜—P0，將P1當(dāng)作新的P0：P0＜—P1，轉(zhuǎn)Step 3。若P1在求解隊(duì)列中，得到P0的父頂點(diǎn)，記為P2，清空臨時(shí)堆棧tempStack，將P0壓入tempStack；

Step 6 將P2壓入臨時(shí)堆棧tempStack。若頂點(diǎn)P2就是頂點(diǎn)P1，或P2、P1屬于同一個(gè)求解隊(duì)列元素，（說(shuō)明求解隊(duì)列中從P1到P0的頂點(diǎn)構(gòu)成了環(huán)路），則轉(zhuǎn)Step7。否則，將P2的父頂點(diǎn)當(dāng)作新的P2：P2＜—F（P2），轉(zhuǎn)Step 6。若頂點(diǎn)P2沒(méi)有父頂點(diǎn)（即P2是起始點(diǎn)），轉(zhuǎn)Step 8；

Step 7 調(diào)整求解隊(duì)列，將臨時(shí)堆棧tempStack內(nèi)所有頂點(diǎn)所在的隊(duì)列元素合并為一個(gè)，將新的隊(duì)列元素置于求解隊(duì)列中P1所在隊(duì)列元素的位置，轉(zhuǎn)Step 4；

Step 8 若求解隊(duì)列中，P1所在隊(duì)列元素在P0所在隊(duì)列元素之后，轉(zhuǎn)Step 4。否則，調(diào)整求解隊(duì)列，將P1所在隊(duì)列元素以及沿著P1傳遞約束方向遍歷到的所有頂點(diǎn)所在的隊(duì)列元素置于P0所在隊(duì)列元素之后，轉(zhuǎn)Step 4；

Step 9 若P0沒(méi)有父頂點(diǎn)（即P0是起始點(diǎn)），則算法至此結(jié)束。若P0有父頂點(diǎn)，則返回P0的父頂點(diǎn)，即將P0的父頂點(diǎn)當(dāng)作新的P0：P0＜-F（P0），轉(zhuǎn)Step 4。

示例 在圖 2約束平衡后執(zhí)行求解隊(duì)列算法，如圖5(b)所示。

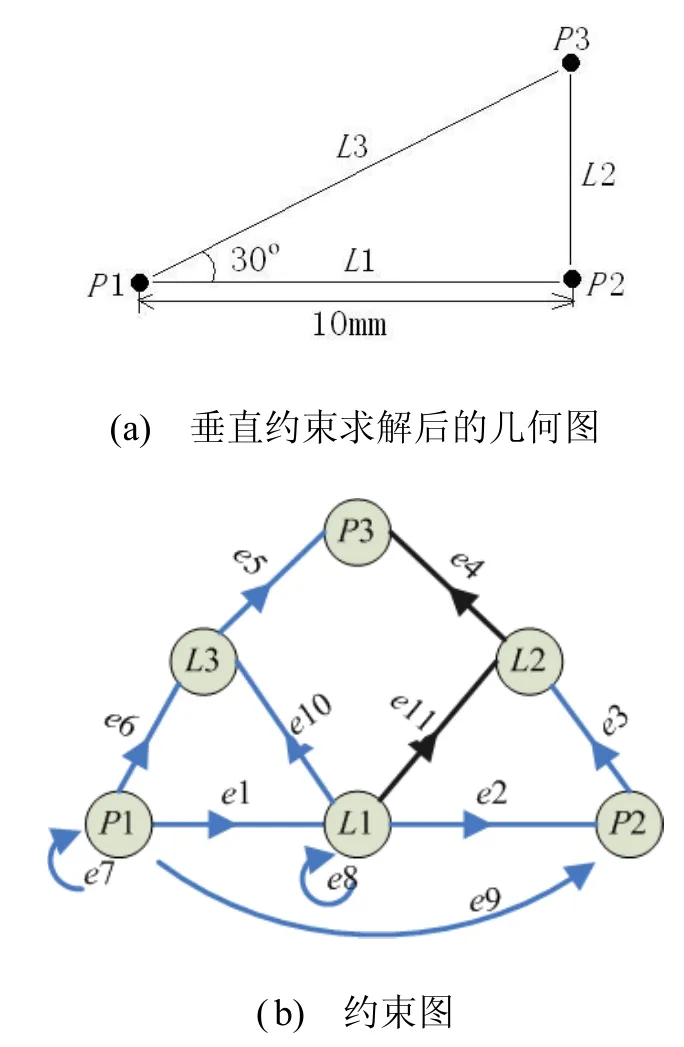
圖5 添加垂直約束后的幾何求解

將新添加垂直約束e11的傳遞頂點(diǎn)L2壓入求解隊(duì)列，求解隊(duì)列變?yōu)椋篖2。遍歷L2的傳遞約束e4，得其傳遞頂點(diǎn)P3，P3不在求解隊(duì)列中，將P3壓入求解隊(duì)列中，求解隊(duì)列變?yōu)長(zhǎng)2—＞P3。P3沒(méi)有傳遞約束，返回到P3的父頂點(diǎn)L2。L2的傳遞約束遍歷完畢，又L2是起始點(diǎn)，算法結(jié)束。最終得到求解隊(duì)列：L2—＞P3，即先通過(guò)幾何L1、P2和約束e11、e3計(jì)算L2，再通過(guò)幾何L2、L3和約束e4、e5計(jì)算P3。最終得到的圖形就是一張滿足所有約束的正確圖形。約束求解后的幾何如圖5中的幾何圖。

4 結(jié) 論

本文提出的約束求解算法概括為：以約束圖為基礎(chǔ)，通過(guò)調(diào)整約束圖平衡約束，通過(guò)求解隊(duì)列算法，提高求解速度，實(shí)現(xiàn)約束求解。該算法已經(jīng)初步應(yīng)用于變量化造型系統(tǒng)中，經(jīng)實(shí)例驗(yàn)證（如圖6），可完成約束高效求解，效果良好。結(jié)論如下：

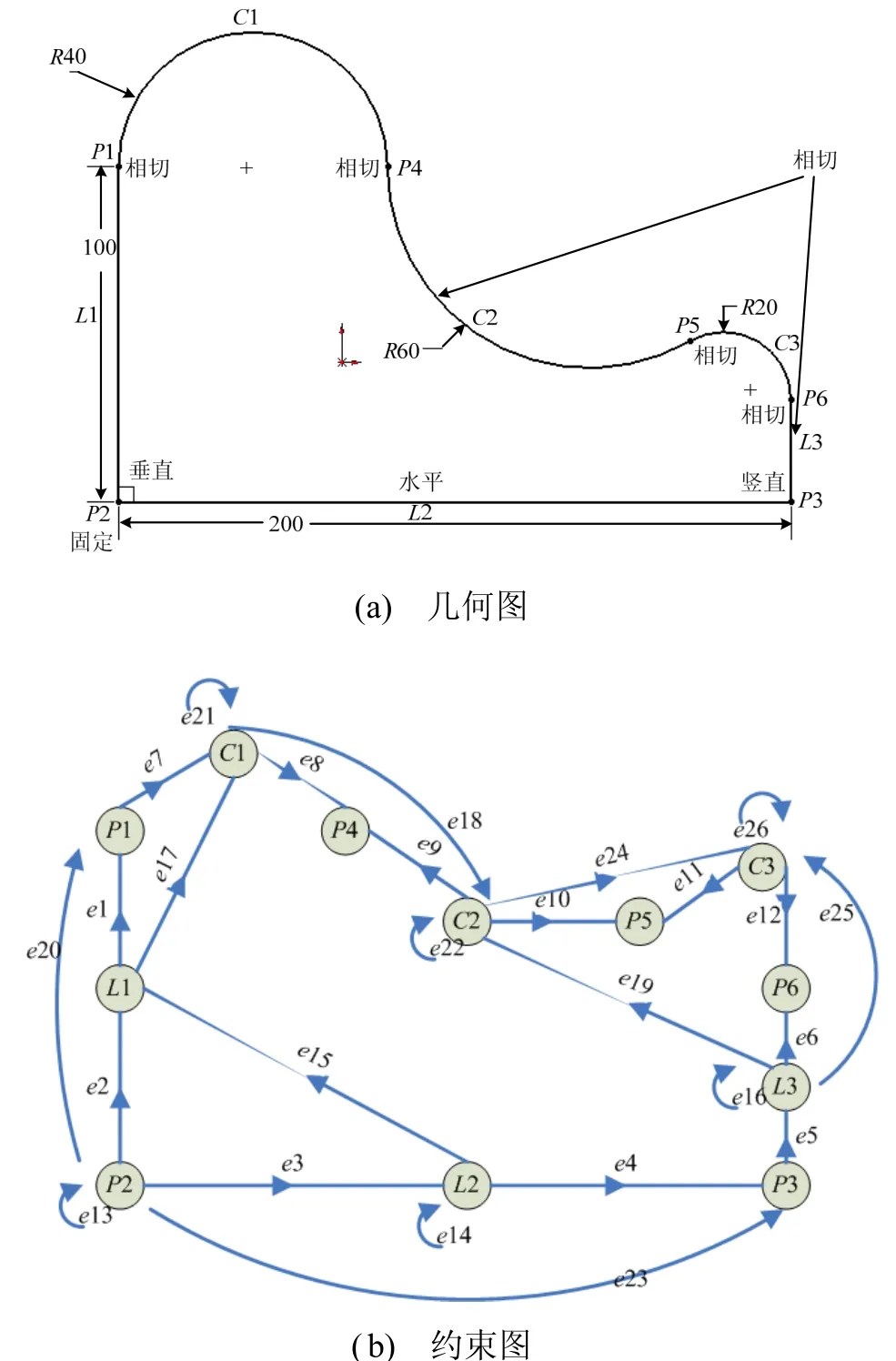
圖6 實(shí)例驗(yàn)證

（1） 約束圖模型解決了復(fù)雜約束信息的管理問(wèn)題。通過(guò)約束圖，將幾何元素和約束有機(jī)的聯(lián)系在一起。

（2） 通過(guò)約束圖的調(diào)整來(lái)平衡約束，進(jìn)行過(guò)約束的判定，可以避免某幾何過(guò)定義導(dǎo)致的無(wú)解方程組計(jì)算；進(jìn)行幾何的完全定義狀態(tài)的判定，可以為設(shè)計(jì)者的設(shè)計(jì)工作提供依據(jù)，提高人機(jī)交互設(shè)計(jì)的效率。

（3） 求解隊(duì)列算法可以在添加或改變約束時(shí)給出需要計(jì)算的幾何以及幾何的計(jì)算順序，將復(fù)雜約束圖進(jìn)行分解，“分而治之”，提高求解效率。

[1] Lee J Y, Kim K. A 2-D geometric constraint solver using DOF based graph reduction [J]. Computer Aided Design, 1998, 30(11): 883-896.

[2] Bouma W, Fudos I, Hoffmann C, et al. A geometric constraint solver [J]. Computer Aided Design, 1995, 27(6): 487-501.

[3] 趙萬(wàn)生, 王 剛, 姜洪臣, 等. 二維欠約束系統(tǒng)求解算法的研究[J]. 哈爾濱工業(yè)大學(xué)學(xué)報(bào), 2002, 34(1): 54-57.

[4] 董金祥, 葛建新, 高 屹, 等. 變參繪圖系統(tǒng)中約束求解的新思路[J]. 計(jì)算機(jī)輔助設(shè)計(jì)與圖形學(xué)學(xué)報(bào), 1997, 9(6): 513-519.

[5] 蔣丹東, 何援軍, 楊 東, 等. 基于點(diǎn)簇歸約的幾何約束求解器研究[J]. 高技術(shù)通訊, 2002, (6): 49-53.

[6] 羅 浩, 陳立平, 周 濟(jì). 基于歸約的幾何約束推理研究[J]. 計(jì)算機(jī)輔助設(shè)計(jì)與圖形學(xué)學(xué)報(bào), 1997, 9(3): 256-262.

2D Geometric Constraint Solving with Directed Graph

WANG Shi-ping, GUO Lian-shui
( School of Mechanical Engineering and Automation, Beijing University of Aeronautics and Astronautics, Beijing 100191, China )

In order to solve the over-constrained problem and enhance computational efficiency, an algorithm, which is based on the constructing directed constraint graph, revealing constraint conflict, then reversing the direction of the related constraint to balance the constraint graph, and finally sorting the graph to get the solving sequence of geometric entities, is presented. The method of balancing constraints can help transforming the over-constrained problem into well-constrained.

computer application; solution of geometric constraint; constraint graph; over-constrained; well-constrained; sort algorithm

TP 391

A

：1003-0158(2010)01-0054-07

2008-07-17

王世平（1983-），男，山東昌邑人，碩士研究生，主要研究方向?yàn)閹缀卧煨图夹g(shù)。