任意多邊形平面載流線圈磁場的空間分布

岑敏銳

(武漢工程大學理學院，湖北 武漢 430074)

0 引 言

載流線圈空間磁場分布的計算是電磁學中的一個常見問題，在各種形狀的載流線圈中，具有軸對稱性的圓形載流線圈研究得比較多[1-5]，而對不具有軸對稱性的多邊形載流線圈的磁場問題則研究得很少，且僅限于一些特殊的多邊形[6-8].本文根據一段載流直導線在空間某點的磁場矢量公式，將多邊形載流線圈視為多段載流導線，然后根據場強疊加原理，給出了求任意多邊形平面載流線圈在空間任意點的磁場分布的方法，并且運用這種方法求出了任意多邊形平面載流線圈磁場的空間分布的普遍表達式.

1 一段載流直導線在空間某點的磁場矢量公式

如圖1所示，一段載流直導線在空間某點P處產生的磁感應強度B的大小為：

(1)

B的方向與電流的方向成右手螺旋關系.

如果只需要求一段載流直導線的磁場分布，根據(1)式，只要知道電流強度I，P點到導線的垂直距離r0，導線與導線端點到P點連線的夾角θ1和θ2，就可以進行求解.但如果需要求的磁場分布是由多段載流直導線組成的多邊形載流線圈所產生的，由于磁感應強度是矢量，而(1)式只考慮了大小，在求空間某點P處的總磁感應強度時，有必要將其改寫為矢量式.

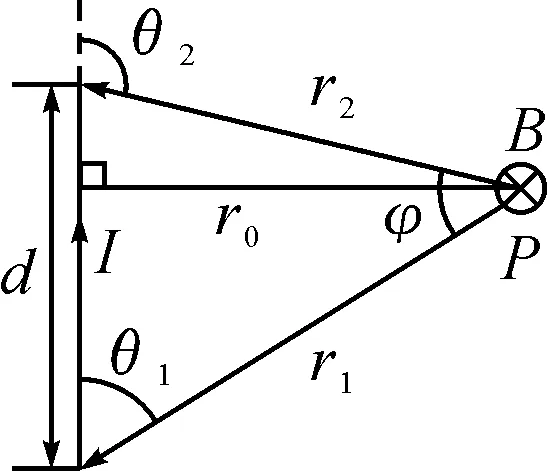
圖1 一段載流直導線的磁場分布

設圖1中載流直導線的長度為d，從P點指向導線兩端點的矢量分別為r1和r2，則點P處的磁感應強度的方向和r1×r2矢量的方向相同.考慮方向后，(1)式中的磁感應強度可以寫成矢量式(2).

(2)

(3)

根據三角形的余弦定理得：

(4)

(5)

(6)

將(4)式、(5)式和(6)式代入(3)式中得：

(7)

如圖2所示，載流直導線P1P2位于Oxy平面之內，從空間某點P(x，y，z)指向P1(x1，y1，0)和P2(x2，y2，0)的矢量分別為r1和r2.

式(7)中矢量r1和r2以及導線長度d分別為：

r1=(x1-x)i+(y1-y)j-zk

(8)

r2=(x2-x)i+(y2-y)j-zk

(9)

(10)

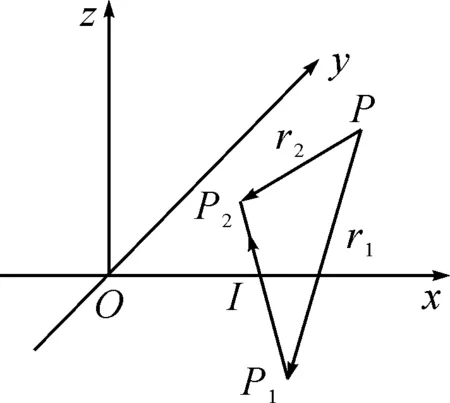
圖2 OXY平面內一段載流直導線的磁場分布

將(8)、(9)和(10)式代入(7)式中得：

(11)

(11)式即為要求的一段載流直導線在空間某點的磁場矢量公式.其中，R、D1和D2分別為：

R=[(x1-x2)2+(y1-y2)2]z2+[(y1-y2)x-

(x1-x2)y+(x1y2-x2y1)]2

(12)

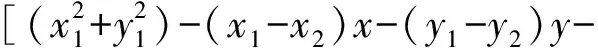
(x1x2+y1y2)]

(13)

(x1x2+y1y2)]

(14)

根據(8)式和(9)式可以算出矢量r1×r2在三個坐標軸上的分量分別為：

|r1×r2|x=z(y2-y1)

(15)

|r1×r2|y=z(x1-x2)

(16)

|r1×r2|z=x1y2-x2y1+xy1-x1y+x2y-xy2

(17)

將(15)、(16)和(17)式代入(11)式中可以求出多邊形任一條邊在空間某點P處產生的磁感應強度在三個坐標軸上的分量分別為：

(18)

(19)

(20)

在求出多邊形任意邊在空間某點P處產生的磁感應強度后，根據場強疊加原理，就可以求出整個線圈在空間的磁場分布.下面以菱形平面載流線圈為例，按照以上方法求出該線圈在空間的磁場分布.

2 菱形平面載流線圈磁場的空間分布

如圖3所示，設有一菱形載流線圈ABCD位于OXY平面之內，各頂點坐標分別為A(a，0，0)、B(0，b，0)、C(-a，0，0)、D(0，-b，0).根據(18)到(20)式分別求出AB、BC、CD和DA四條邊在空間某點P(x，y，z)產生的磁感應強度，再根據場強疊加原理可以求出整個菱形平面載流線圈在P點的磁場分布.

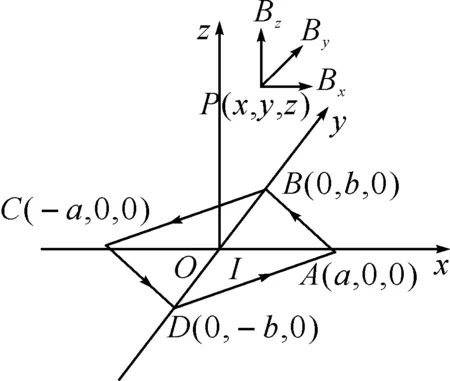
圖3 菱形平面載流線圈的磁場分布

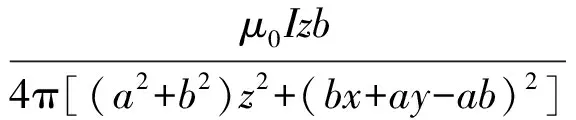
(21)

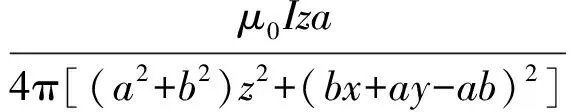
(22)

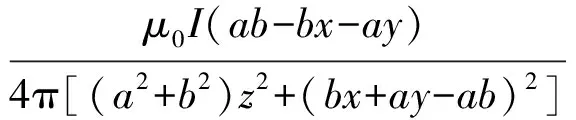
(23)

3 結 語

根據以上分析結果，對于任意多邊形平面載流線圈，只要知道其各頂點在OXY平面上的坐標，代入(18)到(20)式中再求代數和即可得到該載流線圈在空間任意點的磁場分布.方法簡單、明了，易于理解，可以應用到普通物理的教學中.

參考文獻：

[1]李海，張玉穎．圓形線電流的磁感應強度[J].大學物理，1999，18(6)：20-22.

[2]曾令宏.張之翔. 圓環電流的磁場以及兩共軸圓環電流之間的相互作用力[J].大學物理，2002，21(9):14-16，41.

[3]朱平.圓電流空間磁場分布[J].大學物理，2005，24(9):13-17.

[4]張星輝.圓電流磁感線的分布及磁感應強度的函數表達式[J].大學物理，2006，25(1):32-37.

[5]劉耀康.導出圓電流的磁感應強度的簡便方法[J].大學物理，2007，26(7): 32-33.

[6]鄧衛娟，李秉寬.正三角形載流線圈的空間磁場分布[J].廣西物理，2007，28(2): 35-37，39.

[7]鄺向軍.方形載流線圈的空間磁場計算[J].物理與工程，2006，16(1):18-20，25.

[8]岑敏銳. 同軸等大方形線圈的互感系數[J].武漢工程大學學報，2007，29(4):90-92.