基于T-S模型的欠驅動機器人非脆弱保性能H∞控制
吳忠強 劉力靈
燕山大學河北省工業計算機控制工程重點實驗室,秦皇島,066004
0 引言
欠驅動機器人是指獨立控制輸入少于系統自由度的機器人[1],對欠驅動機械臂而言,則是指某個或某些關節沒有驅動裝置,即關節是被動的,也稱自由的。欠驅動機器人由于驅動器的減少而具有質量輕、成本低、能耗低等眾多優點,因此成為機器人研究領域的新熱點[2]。
欠驅動機器人的研究問題包括平衡流形控制、PTP控制、多臂協調操作,甚至其他更復雜的機器人工作任務。為了使欠驅動機器人能像全驅動機器人一樣實現各種靈活的操作,人們基于不同的分析工具和方法,對這類非完整系統進行了深入的研究并提出了多種控制方案(如PID控制、自適應控制[3]、滑模變結構控制[2]、智能控制[1]、魯棒控制[3]等),實現了對某些欠驅動機器人的有效控制。
自T-S模糊建模方法提出以來,基于模糊模型的控制方法已經成為解決某些非線性問題的強有力工具[4-7]。該建模方法通過IF-THEN規則將非線性系統描述為若干個線性子系統的動態組合,先針對線性子系統單獨設計滿足一定性能的控制器,然后在并行分布補償[8](parallel distributed compensation,PDC)設計框架下構建全局控制器,用線性系統理論去分析并解決非線性系統的控制問題。近年來,系統的非脆弱性成為人們感興趣的課題[9-12]。現有文獻多考慮的是線性系統的非脆弱控制問題,對非線性機器人系統的非脆弱控制問題研究較少。
本文研究欠驅動機器人系統的非脆弱保性能H∞控制問題。利用LMI(linear matrix inequality)方法[13],給出模糊非脆弱保性能H∞控制器存在的充分條件,并證明了閉環系統的穩定性。最后用實例仿真驗證了本方法的有效性。
1 欠驅動機器人動力學模型變換
機器人完整的動力學模型描述為

式中,M(q)∈ Rn×n為對稱正定慣性矩陣;C(q,q?)∈ Rn為向心力和哥氏力作用項;G(q)∈Rn為重力作用項;Γ∈Rn為力矩輸入項;q、q?、q¨分別為關節的位置向量、速度向量和加速度向量。
欠驅動機器人的動力學模型可以用以下分塊形式表示

式中,下標a和o分別表示主動關節和被動關節。
由式(2)的第2行得

將式(3)代入式(2)的第1行得

由式(4)可知,適當選取主動關節控制輸入Γa,就可以通過動力學耦合作用控制被動關節到設定角度。在此采用PD型計算力矩控制,控制律表示為

式中,kv、kp分別為恒定對角正定比例矩陣和微分增益矩陣;e為位置誤差,eo=qo-qod;qod為關節期望位置。

將式(5)代入式(4)得誤差方程:式(6)表明如果適當選擇反饋增益矩陣k v、k p,位置誤差可以漸近收斂到零,即可以實現被動關節的位置跟蹤控制。
當被動關節到達期望位置時,鎖定被動關節,系統的動力學模型(式(2))轉化為

2 非脆弱保性能H∞控制器的設計
2.1 T-S模型的建立
系統(式(7))的T-S模糊模型描述如下:

式 中,Nij為 模 糊 集 合,j = 1,2,…,l;X1=為系統的狀態;zj(t)為已知的前件變量;r為模型規則數;Ai和bi為適當維數的已知常數矩陣;ΔAi和Δbi表示系統的不確定性。
對所有的i,用中心平均法解模糊,可得系統模型:

式中,z(t)為向量,其中的元素為已知的前件變量;Nij[zj(t)]為zj(t)對于Nij的隸屬度,并且hi[z(t)]≥0,

將式(10)代入式(9)得

假定式(11)中的 ΔA i和 Δb i有界,且滿足如下約束條件I≤0(文中,矩陣后的符號“>0、<0、≥0、≤0”分別表示矩陣正定、負定、非負定、非正定),其中,D i、E1i、E2i為反映系統不確定性結構的矩陣;F1i為具有Lebesgue可測元素的未知矩陣。將(A i+ΔA i)Q d看作系統擾動 ω,則系統模型可寫為

2.2 控制器的設計
采用PDC結構的模糊控制器,并考慮其脆弱性,有如下模糊控制規則:

整個系統的反饋控制律為

式中,ki為確定的反饋增益矩陣;Δki為控制器的參數變化,表示實現的不確定性。
考慮加法式增益攝動,即Δk i=D fi E fi F f i,其中,D f i、E f i為反映控制器不確定性結構的矩陣;Ffi為具有Lebesgue可測元素的未知矩陣,且滿足FTfiF fi-I≤0。
則閉環系統全局T-S模型為

選被調輸出φ(t)=X。
對系統(式(12))定義系統性能指標:

式中,Q、R為給定的正定加權矩陣。
在給出結論前先給出下列引理。
引理1[12](Schur補引理) 對給定的對稱矩陣其中S11為m ×m維的矩陣。以下3個條件等價:
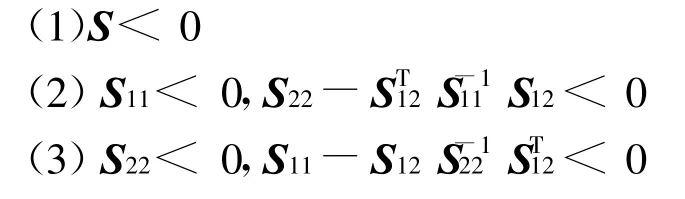
引理2[12]給定適當維數的矩陣Y、D和E,其中Y是對稱的,則有

對所有滿足FTF-I≤0的矩陣F成立,當且僅當存在常數ε>0,使得

定理1 對于給定的系統(式(12)),式(14)的反饋控制律是一個非脆弱保性能H∞控制律,如果存在公共正定矩陣P和k i,使得下列不等式組成立:


式中,εij1、εji1、εij2、εji2、εi1、εi2、ε′、γ為正常數,
下面給出定理1的證明。
取Lyapunov函數
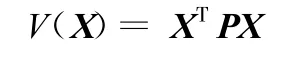
則

Aji=Aj+ΔAj+(bj+Δbj)(ki+Δki)
當 ω(t)為零矩陣時只需保證 Ψ1<0,Ψ2<0,則

由Lyapunov穩定性理論可知系統在無外部擾動時全局漸近穩定。對式(18)兩邊從t=0到t=T積分,因為系統漸近穩定,則X(∞)=0,所以我們可以得到J≤J*=XT(0)PX(0),即該控制律為非脆弱保性能控制律。
當ω(t)為非零矩陣時,對于給定常數γ>0,有

對式(20)兩端從t=0到 t=T積分,可得

因為V(X)≥0,則

即系統為H∞穩定的。

因為PP>0則滿足式(22)即可保證 ψ1<0,ψ2<0,即滿足式(22)則可保證系統是非脆弱保性能 H∞穩定的。令 Φ1= Ψ1+I+PP/γ2,Φ2= Ψ2+2I+2PP/γ2。
下面先求解 Φ1<0成立的充分條件:

應用引理2和Schur補引理我們可以得到Φ1<0的充分條件為存在常數εi1>0,使得式(24)成立:

將式(24)分解,并再次應用引理2和Schur補引理可得式(24)成立的充分條件為存在常數εi2>0,使得式(25)成立:

將式(25)分解,并應用Schur補引理可得式(25)等價于:

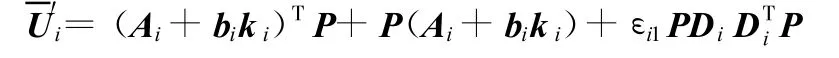
式(26)兩邊分別左右乘diag(P-1,I,I,I,I,I,I,I),并令 θ=P-1,B i=k iθ,即得定理1中的式(16)。
下面求解使 Φ2<0成立的充分條件。應用Petersen引理得


只需保證 Φij<0且 Φji<0便可以實現 Φ2<0。與 Φ1<0成立條件的求解過程相同,可以求得Φij<0成立的充分條件為存在常數εij1>0和εij 2>0使得式(28)成立:


Φji<0成立的充分條件為存在常數εji1>0和εji2>0使得式(29)成立:


式(28)與式(29)相加得到定理 1中的式(17)。定理1得證。
3 仿真研究
為驗證上述方案的正確性,本節對兩連桿串聯機械臂中第一關節為被動關節的情況進行仿真試驗。兩連桿串聯機械臂動力學方程如下:

式中,m1、m2分別為兩桿的質量,m1=m2=1kg;L1、L2分別為兩桿的長度,L1=1m,L2=2m;Lg1、Lg2分別為兩桿的質心距,Lg1=0.5m,Lg2=1m;I1、I2分別為兩桿的轉動慣量,I1=0.083N?m2,I2=0.330N?m2。
針對此系統在控制的第一階段,采用PD型計算力矩控制。控制器參數為kv=3,kp=5。
被動關節被鎖定后,取z=|q1|/|q2|為前件變量,則可以構造如下T-S模型:

假定控制器存在可加性攝動,并且選擇描述不確定性的矩陣為

選取Q為3維單位陣,R取1,應用定理1解LMI可以得到非脆弱保性能H∞控制器的參數

由圖1可以看出,控制的第一階段在PD型計算力矩控制器的作用下,第一關節可以有效實現位置跟蹤。在t=5s時對其進行制動,并采用基于T-S模型的非脆弱保性能H∞控制器,使第二關節實現位置跟蹤。由圖2可以看出,控制的第二階段在基于T-S模型的非脆弱保性能H∞控制器的作用下,即使系統具有擾動且控制器參數發生攝動,第二關節仍然可以在很短的時間內有效的實現位置跟蹤。

圖1 關節1位置誤差曲線

圖2 關節2位置誤差曲線
4 結束語
針對欠驅動機器人系統,將非脆弱控制、保性能控制以及H∞控制結合,提出了基于T-S模型的欠驅動機器人非脆弱保性能H∞控制策略并進行了仿真研究。仿真結果表明被動關節鎖定后,當系統具有外部擾動和控制器參數不確定性時,在基于T-S模型的欠驅動機器人非脆弱保性能H∞控制律的作用下,第二關節能夠實現位置跟蹤。
[1] 方道星,余躍慶,周剛,等.2R平面欠驅動機器人軌跡控制研究[J].中國機械工程,2008,19(9):1016-1021.
[2] 劉慶波,余躍慶.平面2R欠驅動機器人的軌跡規劃與控制[J].中國機械工程,2007,18(24):2899-2902.
[3] 郭益深,陳力.雙臂空間機器人姿態與關節協調運動的自適應控制、魯棒控制[J].中國機械工程,2008,19(6):636-639.
[4] Xie Wei.Improved L2 Gain Performance Controller Synthesis for Takagi-Sugeno Fuzzy System[J].IEEE Transactionsons on Fuzzy Systems,2008,16(5):1142-1150.
[5] Zhou Linna,Zhang Qingling,Yang Chunyu.Local Stability of T-S Fuzzy Systems[J].Control and Decision,2007,22(6):622-625.
[6] Xiu Z H,Wang W.Output Feedback Controller Design of Takagi-Sugeno Fuzzy Systems[J].International Journal of Systems Science,2007,38(2):167-178.
[7] Li J,Zhou S,Xu S.Fuzzy Control System Design via Fuzzy Lyapunov Functions[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B:Cybernetics,2008,38(6):1657-1661.
[8] Zhou Linna,Zhang Qingling,Hu Yuebing,et al.Stability Analysis and Synthesis of T-S Fuzzy Systems[J].Control Theory and Applications,2007,24(6):886-890.
[9] 張樂,井元偉.基于非脆弱控制器設計的不確定模糊系統穩定性研究[J].控制與決策,2007,22(3):329-332.
[10] Oya H,Hagino K.Trajectory-based Design of Robust Non-fragile Controllers for a Class of Uncertain Linear Continuous-time Systems[J].International Journal of Control,2007,80(12):1849-1962.
[11] Yang Jun,Zhong Shouming,Xiong Lianglin.A Descriptor System Approach to Non-fragile H∞Control for Uncertain Fuzzy Neutral Systems[J].Fuzzy Sets and Systems,2009,160(4):423-438.
[12] 俞立.魯棒控制——線性矩陣不等式處理方法[M].北京:清華大學出版社,2002.
[13] Henry D,Zolghadr I A.Design of Fault Diagnosis Filters:a Multi-objective Approach[J].Journal of the Franklin Institute,2005,342(4):421-446.

