一種考慮精度和效率的微運動測量算法

盧清華 張憲民 范彥斌

1.佛山科學技術學院,佛山,528000 2.華南理工大學,廣州,510640

0 引言

微納制造技術的高速發展給計量科學和計量儀器提出了新的測量任務,測量精度提高到納米級甚至亞納米級[1]。在設計開發MEMS時,系統功能主要是通過微結構的微小位移和變形來實現的,因此對MEMS的微小位移和速度等微運動的測量成為開發MEMS的關鍵[2]。此外,納米級精度微位移檢測技術也是研究納米級精密工作臺的關鍵技術之一[3]。因此,研究高精度的微運動測量方法對研究微納制造技術具有重要的意義。

微運動測量技術近年來取得了長足的進步,研究者們提出了許多測量微運動的運動估計算法[4-10]。基于梯度的運動估計算法在微運動測量中得到了廣泛的應用。Timoner等[4]設計了一種基于梯度的多圖像微運動測量方法。該方法在測量小于1個像素的硅微機械運動時,精度達到了納米級。盧清華等[8]設計了一種魯棒多尺度微運動測量方法,該方法與計算機微視覺相結合能夠測量納米級精度的微運動。然而,研究者們在設計上述微運動測量方法時,大多數只考慮了算法的精度,并沒有考慮算法的效率。在實際應用中,無論一種微運動測量算法多么精確,除非它能夠在規定的響應時間內完成微運動測量,否則該算法是沒有用的。因此,實際應用中的微運動測量算法,必須同時考慮其精度和效率[11]。

本文同時考慮算法的精度和效率,設計了一種基于梯度的微運動測量算法。根據微運動測量算法的精度和效率性能評估準則,通過設置算法的不同參數,找到總體性能表現較好的微運動測量方法。

1 考慮精度和效率的微運動測量算法

1.1 基于梯度的運動估計算法

基于梯度的運動估計算法[4,7-8]一般都是根據常亮度假設[12]提出的。根據這種假設有

通過計算多個不同位置的圖像梯度,式(1)轉化為一個有兩個未知量d x和d y的超約束方程組。為了簡化,采用 Ix、Iy及It分別表示圖像梯度則利用最小二乘法求解該方程組有

式(2)中,在所有的i、j及t范圍內求解 d x和d y的值,其中,i=1,2,…,M-1;j=1,2,…,N-1,M×N表示測量圖像的最大像素數。

從式(2)可以看出,只要找到圖像的梯度,就可以求得d x和d y的值。最初,人們一般采用一階微分的方法計算圖像的梯度[12],但是該方法的運動估計精度不高。為了提高測量精度,將微運動測量看成是信號處理問題,采用濾波器方法計算圖像的梯度[4,7-8]。采用該方法,圖像任意位置處的梯度可以使用濾波器對圖像的行和列分別進行卷積得到

式中,I1(x,y,t)和I2(x,y,t)為兩幅相鄰測量圖像的亮度函數;g表示微分濾波器;h表示插補濾波器;*表示卷積。

式(3)表明,只要選取合適的濾波器,就可以很快地計算圖像的梯度進而估計d x和d y的值。此外,采用多尺度方法,可以進一步提高微運動測量算法的測量精度[7-8]。

基于梯度的微運動測量算法中,研究者們只考慮了算法的精度,并沒有考慮算法的效率。本文根據微運動測量算法的性能評估準則,采用同時考慮算法精度和效率的微運動測量算法測量微運動。

1.2 微運動測量算法的精度和效率評估

評估一種實際應用中的運動估計算法,必須同時考慮算法的精度和效率[11]。在文獻[13]中,同時考慮算法的精度和效率,提出了一種評估基于梯度運動估計算法總體性能的偏差-時間曲線圖方法。在該評估方法中,以測量偏差作為算法的精度性能準則,以算法的執行時間表征算法的效率,通過設置運動估計算法的不同參數值繪制評估算法性能的偏差-時間曲線。對于基于梯度的運動估計算法,這些參數一般是指用于預平滑處理或用于計算圖像梯度的濾波器的抽頭數。對一些復雜的運動估計算法,可能還需要考慮其他參數。此外,該性能曲線中的算法偏差和執行時間是在相同條件下得到的。

圖1給出的是微運動測量算法用于測量某一微運動時的性能評估曲線示例。如圖1所示,x軸表示算法用于測量某一特定運動時偏差的絕對值,y軸表示算法的相應執行時間。性能評估圖中的性能點離原點越近,即對應著算法的偏差越小或執行時間越短,則該算法的性能越好。算法1的測量精度大于算法2的測量精度,但是算法2的性能點離原點更近,也就是算法2的總體性能好于算法1。這意味著,如果同時考慮算法的精度和效率,則一種測量算法的精度越高并不能保證其總體性能越好。在圖1中,通過設置算法3的不同參數繪制了該算法的性能評估曲線。算法3在A點處的估計性能好于算法B點和C點處的性能。

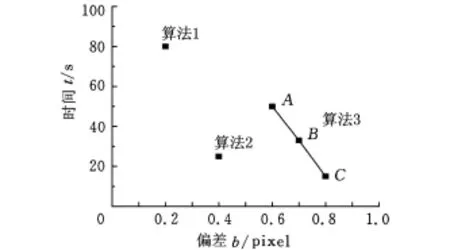
圖1 微運動測量算法性能評估示例

采用基于梯度的微運動測量算法測量微運動時,根據評估算法總體性能的偏差-時間曲線,選取用于計算測量圖像梯度的濾波器抽頭數和用于改善測量精度的多尺度方法的尺度層數,進行微運動測量。這種將算法的性能評估和基于梯度的算法相結合的方法用于微運動測量時,不僅考慮了算法的精度,而且考慮了算法的效率。

圖2 測試圖像

2 實驗模擬與分析

在實驗模擬中,為了驗證提出的同時考慮了精度和效率的微運動測量方法的性能,將一幅256×256個像素的MEMS硅微機械光學顯微鏡圖像作為測試圖像,如圖2所示[14]。在實際應用中,圖像都會受到噪聲污染,為了驗證提出的算法測量噪聲圖像時的性能,在仿真時將測試圖像加入均值為0、標準差為0.003 15的高斯噪聲[4]。在所有實驗模擬中,未經特殊說明的仿真結果報告的偏差均為平移運動測量偏差的絕對值。所有測試均為dx=dy時的運動估計結果,此時的運動估計偏差最大[15]。此外,所有算法均在Pentium Dual 2.20GHz、內存2GB的臺式機上實現。

圖3給出的是只考慮精度的微運動測量算法測量偏差的對比。在圖 3中,5-Farid和7-Farid分別表示采用5抽頭Farid濾波器[16]和7抽頭Farid濾波器并根據式(3)計算梯度的微運動測量方法。M 3-5-Farid表示5抽頭Farid濾波器和3層高斯金字塔多尺度迭代方法相結合的微運動測量方法,M 3-7-Farid表示7抽頭Farid濾波器和3層高斯金字塔多尺度迭代方法相結合的微運動測量方法。從圖3可以看出,只考慮微運動測量算法的精度時,用于計算圖像梯度的濾波器抽頭數越大,算法測量偏差越小。特別地,采用多尺度方法,測量算法的精度得到了很大的提高。圖3顯示的結果也表明,M3-5-Farid方法和M 3-7-Farid方法的測量偏差相接近。這是由于5抽頭和7抽頭的Farid濾波器在測量小運動時精度相近,而多尺度方法是將大運動分解為多個小運動進行測量的,于是測量圖像采用多尺度方法分解后,5抽頭和7抽頭濾波器測量的運動均較小,于是這兩種方法的測量偏差幾乎相同。

圖3 不同方法的測量偏差比較

圖4 是圖3所示方法的偏差-時間性能圖。在圖4中,表征精度性能的偏差為指定平移范圍內所有偏差絕對值的總和,算法的執行時間取指定平移范圍內使用MATLAB 7.0估計所有平移運動的總時間。從圖4可以看出,7-Farid方法的性能點離性能圖的原點最近,總體性能表現最好。5-Farid方法的執行時間最短,但是其總偏差最大。M3-7-Farid方法的總偏差最小,而執行時間最長。這意味著,如果同時考慮算法的精度和效率,精度最高的微運動測量算法的總體性能并一定最好。圖4表明,M 3-5-Farid方法和M3-7-Farid方法與原點的距離相接近,這兩種方法的總體性能表現相類似。但是,M3-7-Farid方法的總偏差略小于M3-5-Farid方法,在實際應用中,更趨向于采用M3-7-Farid方法用于微運動測量。

圖4 不同測量方法的總體性能比較

圖5 給出的是不同多尺度方法的總體性能比較。在圖5中,偏差和時間的含義與圖4中的相同。其中,M5-7-Farid表示7抽頭Farid濾波器和5層高斯金字塔多尺度迭代方法相結合的微運動測量方法。從圖5可以看出,采用3層多尺度方法的M 3-7-Farid方法性能點與原點的距離比采用5層多尺度方法的M 5-7-Farid方法性能點到原點的距離小很多,也就是M3-7-Farid方法的總體性能明顯好于M 5-7-Farid方法。雖然采用5層多尺度方法的精度相對于3層多尺度方法得到了一定的提高,但是相應地大幅度增加了算法的執行時間。如果同時考慮算法的精度和效率,這種大量犧牲微運動測量算法的效率而提高精度的方法并不適合于實際應用。綜上所述,同時考慮算法的精度和效率,采用7抽頭Farid濾波器計算圖像的梯度并結合3層金字塔多尺度迭代方法的M 3-7-Farid算法是一種總體性能表現較好的微運動測量方法。此外,圖5表明了該方法在測量大約2個像素的MEMS硅微機械光學顯微鏡圖像時,最大測量偏差小于0.025個像素。

圖5 不同多尺度測量方法的總體性能比較

3 結束語

同時考慮算法的精度和效率,結合基于梯度的運動估計方法,提出了一種總體性能表現較好的微運動測量方法。在設計該微運動測量方法時,根據算法的偏差-時間性能評估曲線,選取測量算法的合適參數(如濾波器抽頭數或多尺度方法的尺度層數),找到總體性能表現較好的微運動測量方法。分析表明,設計基于梯度的微運動測量算法時如果同時考慮精度和效率,則增加用于計算梯度的濾波器的抽頭數或多尺度方法的尺度層數并不一定能提高算法的總體性能。此外,實驗模擬表明了提出的微運動測量方法不但總體性能表現較好,而且在測量大約2個像素的MEMS微運動圖像時最大測量偏差小于0.025個像素。

[1] 蔣莊德,徐通模.微納制造技術及微系統的發展現狀、趨勢及展望[R/OL].裝備制造(電子版),2006,2.[2009-12-22].http：//www.chinaem.cn/dzkw/06-2/12.htm.

[2] 王濤,王曉東,王立鼎,等.MEMS中微結構動態測試技術進展[J].中國機械工程,2005,16(1)：83-88.

[3] 盧秉恒.微納制造[R].北京：國家自然科學基金委員會,2004.

[4] Timoner S J,Freeman D M.Multi-image Gradient-based Algorithms for Motion Estimation[J].Opt.Eng.,2001,40(9)：2003-2016.

[5] Gupta N,Kanal L.Gradient Based Image Motion Estimation without Computing Gradients[J].International Journal of Computer Vision,1997,22(1)：81-101.

[6] Davis C Q,Freeman D M.Statistics of Subpixel Registration Algorithms Based on Spatiotemporal Gradients or Block Matching[J].Opt.Eng.,1998,37(4)：1290-1298.

[7] Lu Q H,Zhang X M.Multiscale MSE-minimizing Filters for Gradient-based Motion Estimation[J].Measurement,2007,40：841-848.

[8] 盧清華,張憲民,范彥斌.基于計算機微視覺的魯棒多尺度平面微運動測量[J].機械工程學報,2009,45(2)：164-169.

[9] 陳治,胡曉東,傅星,等.基于塊匹配的MEMS平面納米精度運動測量[J].光學精密工程,2008,16(3)：505-509.

[10] 白金鵬,史鐵林,謝勇君,等.基于頻閃干涉的微結構三維運動測量方法[J].測控技術,2008,27(6)：5-8.

[11] Liu H C,Hong T H,Herman M,et al.Accuracy vs Efficiency Trade-offs in Optical Flow Algorithms[J].Computer Vision and Image Understanding,1998,72(3)：271-286.

[12] Horn B K P,Schunck B G.Direct Methods for Recovering Motion[J].International Journal of Computer Vision,1988(2)：51-76.

[13] 盧清華,張憲民,范彥斌.一種運動估計算法的性能評估方法[J].工程圖學學報,2009,30(5)：113-118.

[14] Freeman D M,Alexander JA,Michael JG,et al.Multidimensional Motion Analysis Using Computer Microvision[R/OL].[2009-12-18].http：//umech.mit.edu/freeman/talks/sssaw98/talk3.html.

[15] Robinson D,Milanfar P.Bias-minimizing Filters for Gradient-based Image Registration[J].Signal Processing：Image Communication,2005,20：554-568.

[16] Farid H,Simoncelli E P.Differentiation of Discrete Multidimensional Signals[J].IEEE Transactions on Image Processing,2004,13(4)：496-508.