ZK60鎂合金高溫流變本構模型

覃銀江，潘清林，何運斌，李文斌，劉曉艷，范曦

(中南大學 材料科學與工程學院，湖南 長沙，410083)

ZK60鎂合金作為一種高強度的變形鎂合金，其比強度已超過高強度的7075鋁合金，極有可能取代大部分鋁合金[1]。但是，該合金中 Zn的質量分數為5.0%～6.0%，雖可使合金具有很高的強度，但此成分點在合金熱裂區范圍內，使鑄錠的后續加工困難[2]。此外，鎂合金具有密排六方結構，室溫下滑移系較少，使其塑性變形能力較差，變形需在高溫下進行，且各種熱加工工藝條件對鎂合金的變形行為有顯著的影響[3-4]。因此，研究ZK60鎂合金熱變形行為、建立流變應力本構方程對深入了解其變形規律有重要意義。金屬熱變形流變應力是材料在高溫下的基本性能，它受變形溫度、變形程度、應變速率和合金化學成分的影響，也是變形體內部顯微組織演變的綜合反映，在制定熱加工工藝以及金屬塑性變形理論的研究時是極其重要的參數[5]。隨著計算機技術的快速發展，有限元(FEM)等數值模擬方法在金屬塑性成型的研究中得到越來越廣泛的應用，而建立精確的流變應力模型是提高數值模擬精度的關鍵。因此，許多研究者對金屬熱變形流變應力本構模型進行了研究并取得了很大的進展[6-12]。但是，在這些研究中，除Takuda等[8,10]提出的模型外，其余均未考慮應變對流變應力的影響。由于鎂合金的層錯能低、滑移系少、晶界擴散速率高，在熱加工時極易發生動態再結晶[13-14]，流變應力隨應變變化明顯。要更精確地描述鎂合金流變應力變化規律就必須考慮應變對流變應力的影響。本文作者在變形溫度為523～673 K和應變速率為0.001～1 s-1條件下對ZK60鎂合金進行高溫熱壓縮，研究合金流變應力變化規律，建立包含變形溫度、應變速率和應變的流變應力本構方程。

1 實驗方法

實驗用 ZK60鎂合金的化學成分為 Mg-5.78Zn-0.76Zr(質量分數，%)。鑄態合金經673 K保溫 12 h均勻化退火后加工成直徑×高為10 mm×15 mm的圓柱形試樣。壓縮試驗在Gleeble-1500熱模擬機上進行。通過其自動控制系統在預設的溫度和應變速率下進行恒溫、恒應變速率壓縮。試樣壓縮前的升溫速度為10℃/s，在加熱到預定變形溫度之后保溫3 min。為減小試樣與壓頭之間的摩擦，在壓縮試樣兩端分別加工 1個厚度為 0.2 mm 的凹槽以填充潤滑劑(75% 石墨+20%機油+5% 硝酸三甲苯脂)。實驗應變速率為0.001，0.01，0.1和1 s-1，變形溫度為523，573，623和673 K，總壓縮變形量為60%。

2 結果與分析

2.1 真應力-真應變曲線

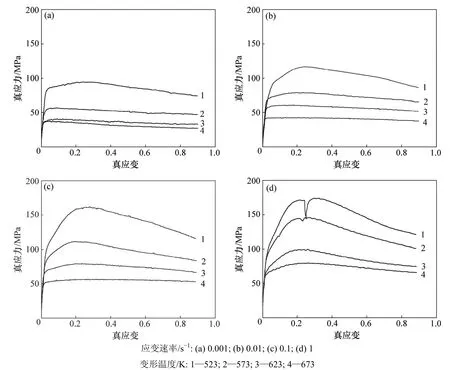
圖1 ZK60鎂合金不同應變速率下的真應力-真應變曲線Fig.1 True stress-true strain curves of ZK60 magnesium alloy at different strain rates

圖1 所示為ZK60鎂合金不同變形條件下的真應力-真應變曲線。從圖1中可以看出，ZK60鎂合金真應力-真應變曲線具有典型的動態再結晶特征。在實驗應變范圍內，應力-應變曲線可劃分為 4個階段：階段Ⅰ(加工硬化階段)，階段Ⅱ(過渡階段)，階段Ⅲ(軟化階段)和階段Ⅳ(穩態流變階段)。在階段Ⅰ(加工硬化階段)，由于大量位錯的產生和交互作用，使晶體中產生許多障礙和缺陷，阻礙位錯的進一步運動，合金變形抗力隨著應變增加而急劇增大，此時，加工硬化率大于軟化率；在階段Ⅱ(過渡階段)，動態回復和部分動態再結晶的軟化作用抵消了部分加工硬化作用，使合金的加工硬化率減小，當軟化作用和硬化作用相等時，流變應力曲線達到峰值；在階段Ⅲ(軟化階段)，動態再結晶軟化作用超過了加工硬化作用，使流變應力隨著應變增加而降低；當加工硬化與動態再結晶軟化再次達到平衡時，流變應力即進入階段Ⅳ(穩態流變階段)。在溫度較高和應變速率較低時，由于合金很快發生再結晶，以上所述的階段Ⅱ(過渡階段)變得不明顯甚至消失。

從圖1可看出：在應變速率為1 s-1，變形溫度為523 K時的真應力-真應變曲線很不規則，說明在此條件下變形時試樣發生了宏觀開裂，ZK60鎂合金在低于523 K下變形比較困難。這是因為：當溫度較低時，多晶鎂的塑性變形僅局限于基面{0 001}滑移和錐面{孿生，因此，鎂合金變形時只有3個幾何滑移系和2個獨立滑移系，易在晶界處產生大的應力集中；當變形量較大時，沿孿生區域(尤其在壓縮時)或沿大晶粒的基面產生局部穿晶裂紋，這就使得鎂合金在低溫下很難加工[15]。

圖2所示為各變形條件下的流變應力水平σ(此處以峰值應力代表)與變形溫度T和應變速率ε的關系。圖 2表明：在應變速率一定時，ZK60鎂合金流變應力隨著溫度的升高而降低；當變形溫度一定時，合金流變應力隨著應變速率增大而升高。這是因為當變形溫度升高時，原子的熱激活作用加劇，位錯的活動能力增強，在變形過程中可以有更多的位錯進行滑移和攀移，從而使軟化過程更為突出，流變應力降低；隨著應變速率的增加，單位時間內產生的位錯密度增加，位錯運動受阻，位錯攀移及位錯反應等引起的軟化速率相對降低，硬化增強，使合金的臨界切應力升高，導致流變應力增大。同時，合金的變形時間縮短，使得單位時間內動態再結晶的形核數目減少，軟化程度降低，間接地也使合金的流變應力增大。

2.2 流變應力本構方程的建立

為了更進一步描述ZK60鎂合金流變應力與變形溫度、應變速率以及應變的關系，下面建立ZK60鎂合金的流變應力本構方程。

對不同條件的熱加工數據進行研究，結果表明流變應力σ與變形溫度T、應變速率ε˙之間的關系可用下式描述[16-20]：

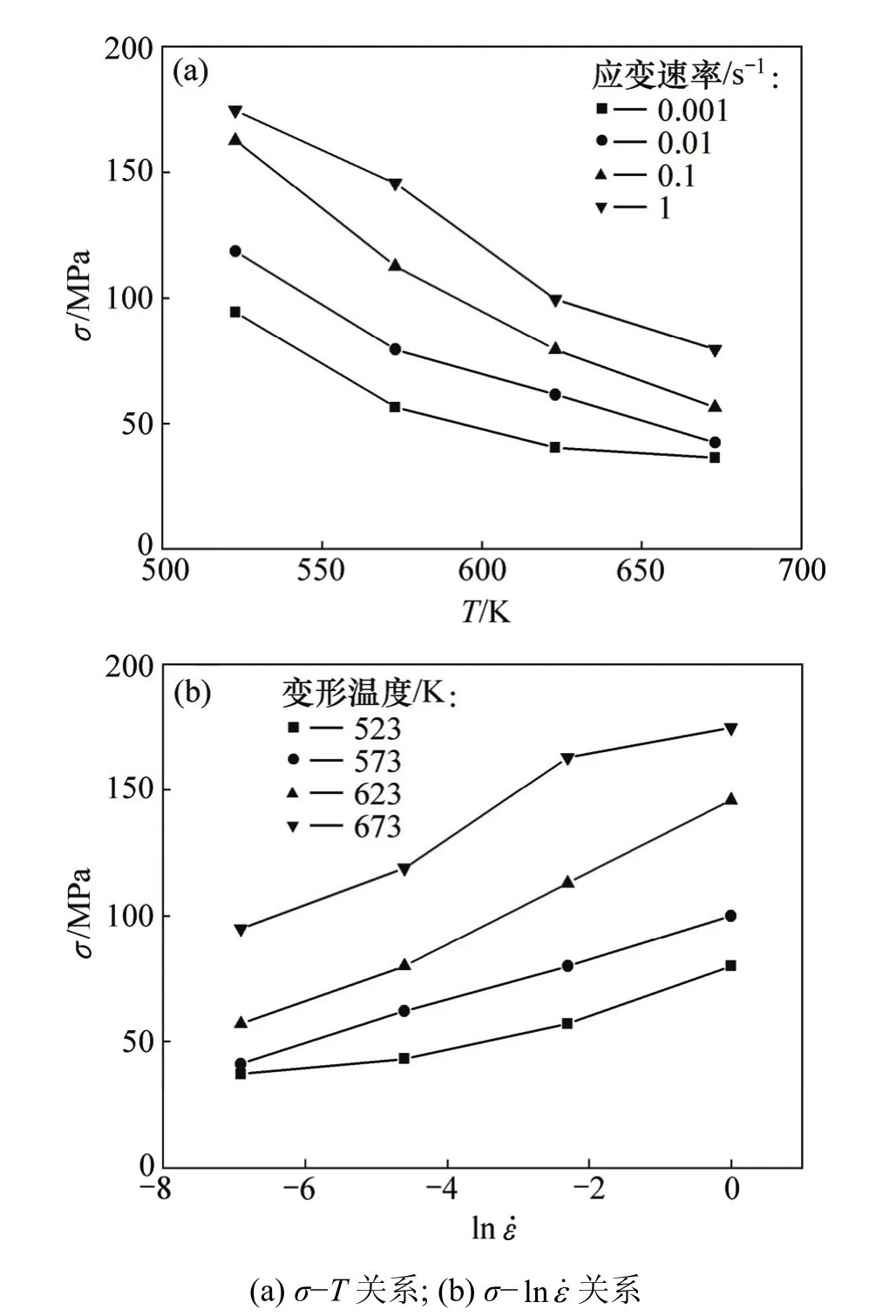
圖2 變形參數對流變應力的影響Fig.2 Effects of processing parameters on flow stress

式中：F(σ)為應力函數。F(σ)具有以下3種形式。(1) 在低應力水平(ασ＜0.8)時，

(2) 在高應力水平(ασ＞1.2)時，

(3) 對所有應力水平，

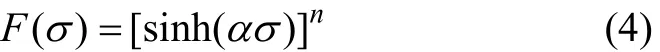
其中：A，α，n和β均為常數，且滿足α=β/n；ε˙為應變速率；Q為變形激活能；T為熱力學溫度；R為摩爾氣體常數；σ為流變應力。

在低應力和高應力水平下，分別將式(2)和式(3)代入式(1)，并對兩邊取對數整理后可得：

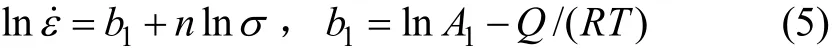
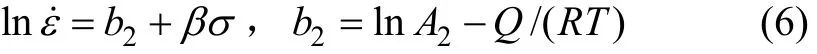
取不同條件下的峰值應力為流變應力，作lnlnεσ-˙和lnεσ-˙關系曲線，并分別進行線性回歸，結果分別如圖3(a)和3(b)所示。根據式(5)和式(6)，取圖 3(a)中低應力的 3條直線斜率的平均值得 n=7.853 1，取圖3(b)中高應力的2條直線斜率的平均值得 β=0.077 MPa-1，可得：α=β/n=0.009 8 MPa-1。

Zener等[21]提出變形溫度和應變速率對流變應力的影響可以用Z參數來描述。在所有應力狀態下，有：

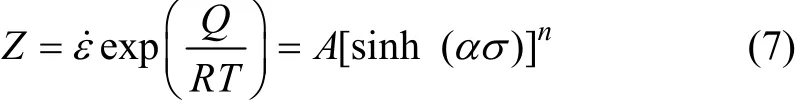
對式(7)求偏微分可得變形激活能Q的計算式為：

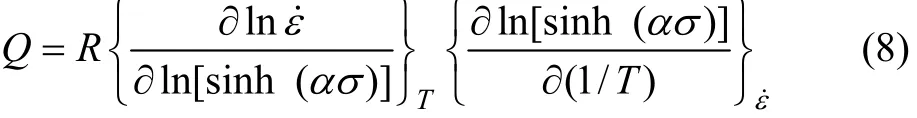
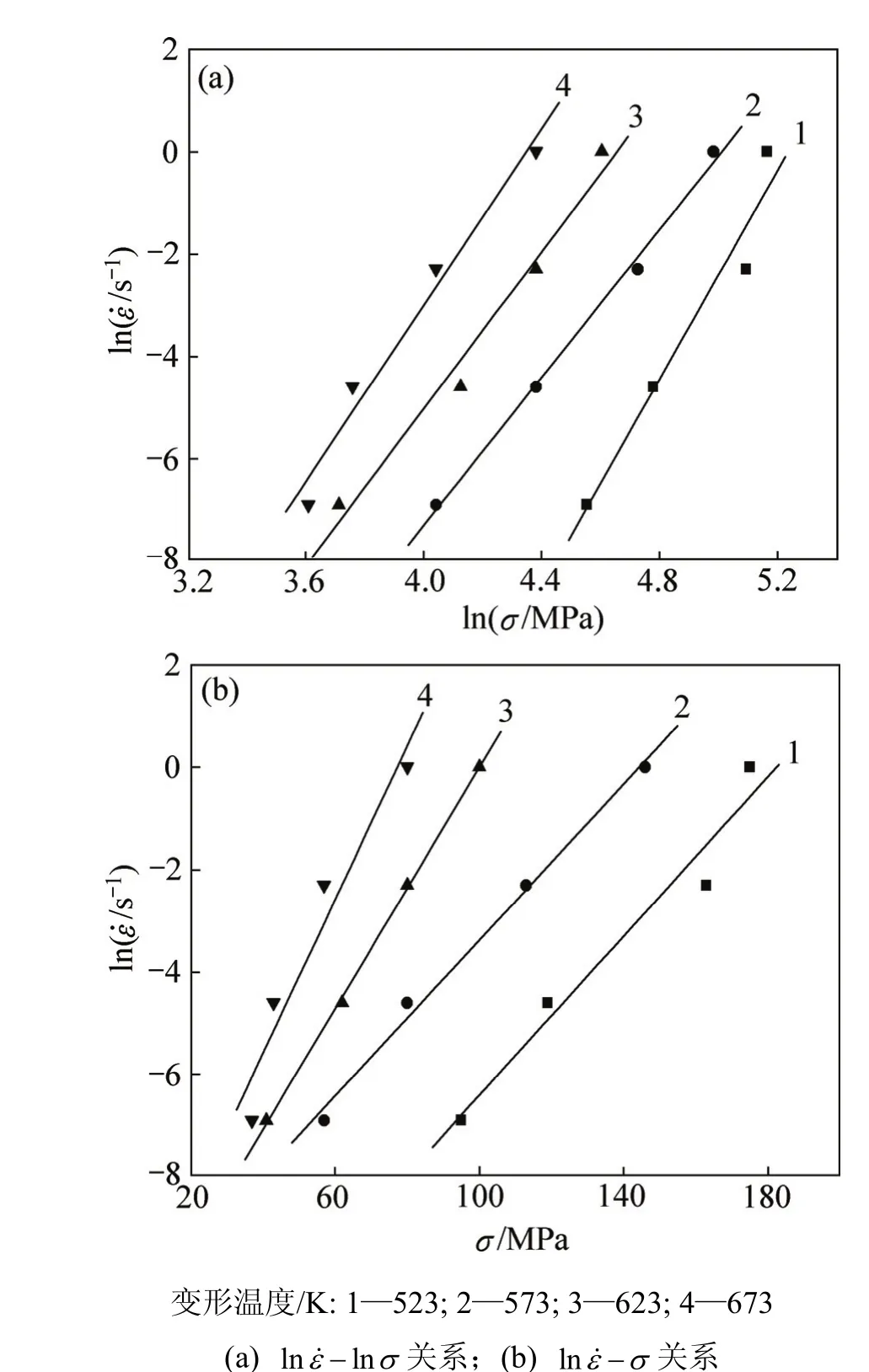
圖3 峰值應力與應變速率的關系Fig.3 Relationships between peak stress and strain rate

取峰值應力為流變應力，作出lnε˙-ln[sinh (ασ)]和ln[sinh (ασ)]-T-1關系曲線，并進行線性回歸，分別如圖4(a)和4(b)所示。取2個圖中4條直線的平均值6.751 9和2.831 0分別為式(8)中第1個偏導和第2個偏導值，于是，可計算變形激活能Q=158.919 kJ/mol。

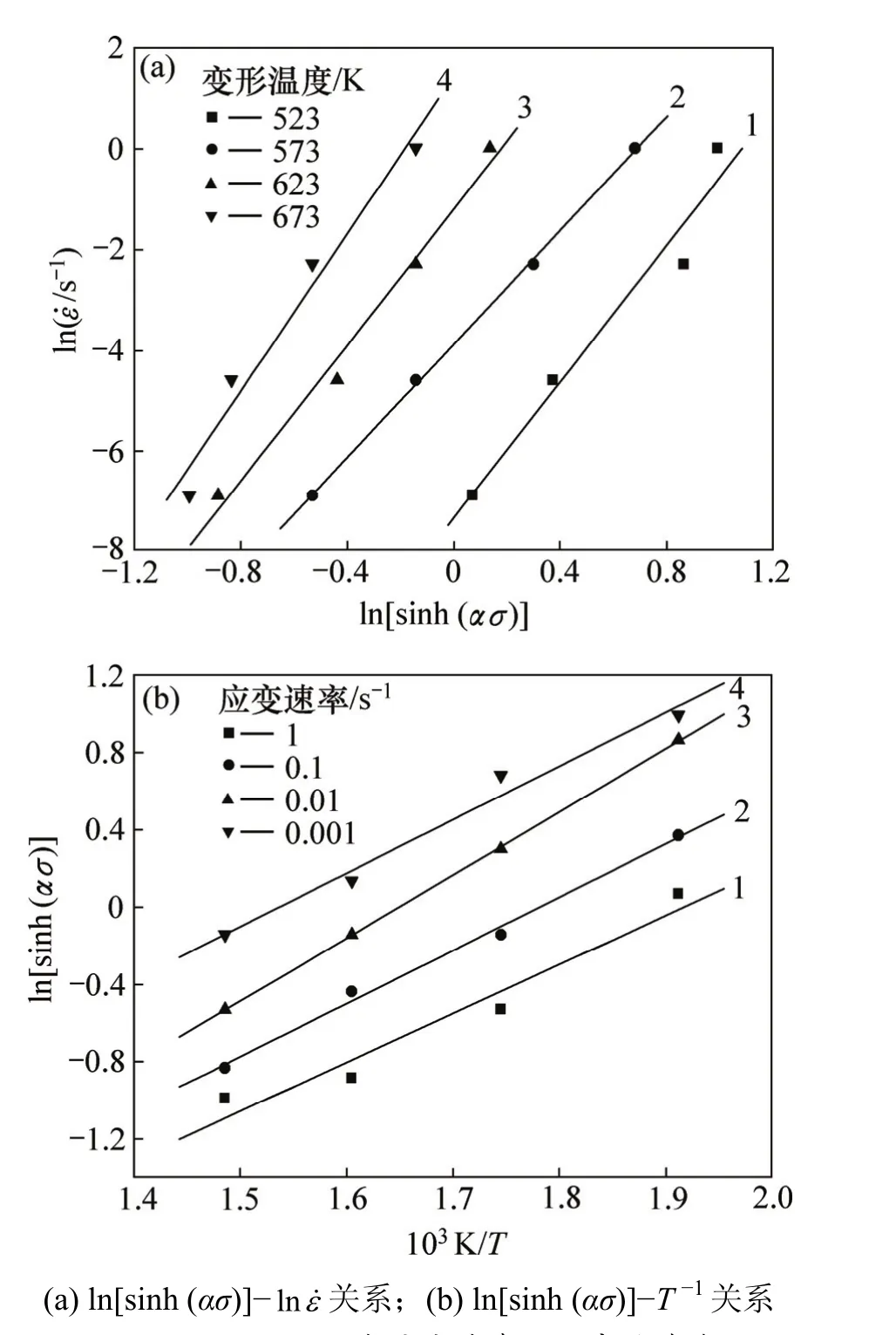
圖4 ln[sinh (ασ)]與應變速率和溫度的關系Fig.4 Relationships of lnε˙-ln[sinh (ασ)] and ln[sinh (ασ)]-T -1

對式(7)兩邊取對數還可得到：

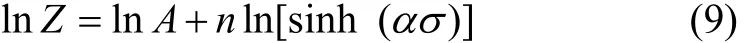
根據式(9)，對ln Z-ln[sinh (ασ)]數據進行線性回歸(圖5)，即可得到n=6.666 4，ln A=29.300 3。于是，可得A=5.308 3×1012s-1。

由式(7)再根據雙曲正弦函數反函數公式可得：

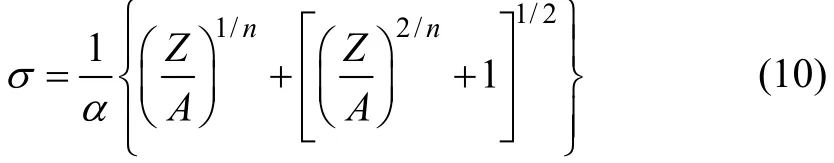
將以上計算得到的α，Q，n和A代入式(7)和式(10)即可算出各個變形條件下的峰值應力，與實測值的比較見表1。其中相對誤差的計算式為：

圖 5 ln Z-ln[sinh (ασ)]關系Fig.5 Relationship between ln Z and ln[sinh (ασ)]

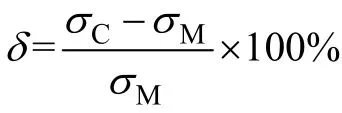
其中：Mσ和Cσ分別為鎂合金流變應力實測值和計算值。從計算結果可以看出：峰值應力計算值與實測值較符合，不同應變速率下的平均相對誤差最大值僅為1.683%。

由以上分析可知：當變形溫度較低、應變速率較高時，ZK60鎂合金的流變應力曲線由不同的4個階段組成，各個階段應力隨應變而發生變化。為了更好地描述熱壓縮過程中的流變應力行為，以便為熱加工數值模擬提供更加精確的流變應力，就必須考慮應變對流變應力的影響。

本文在應變為0.1～0.8(步長為0.05)的范圍內，采用前述的處理峰值應力的方法計算不同應變下的 α，Q，n和A，得出α，Q，n和A與應變的關系如圖6所示。采用以下的多項式對各個參數進行擬合，其擬合結果見表2。

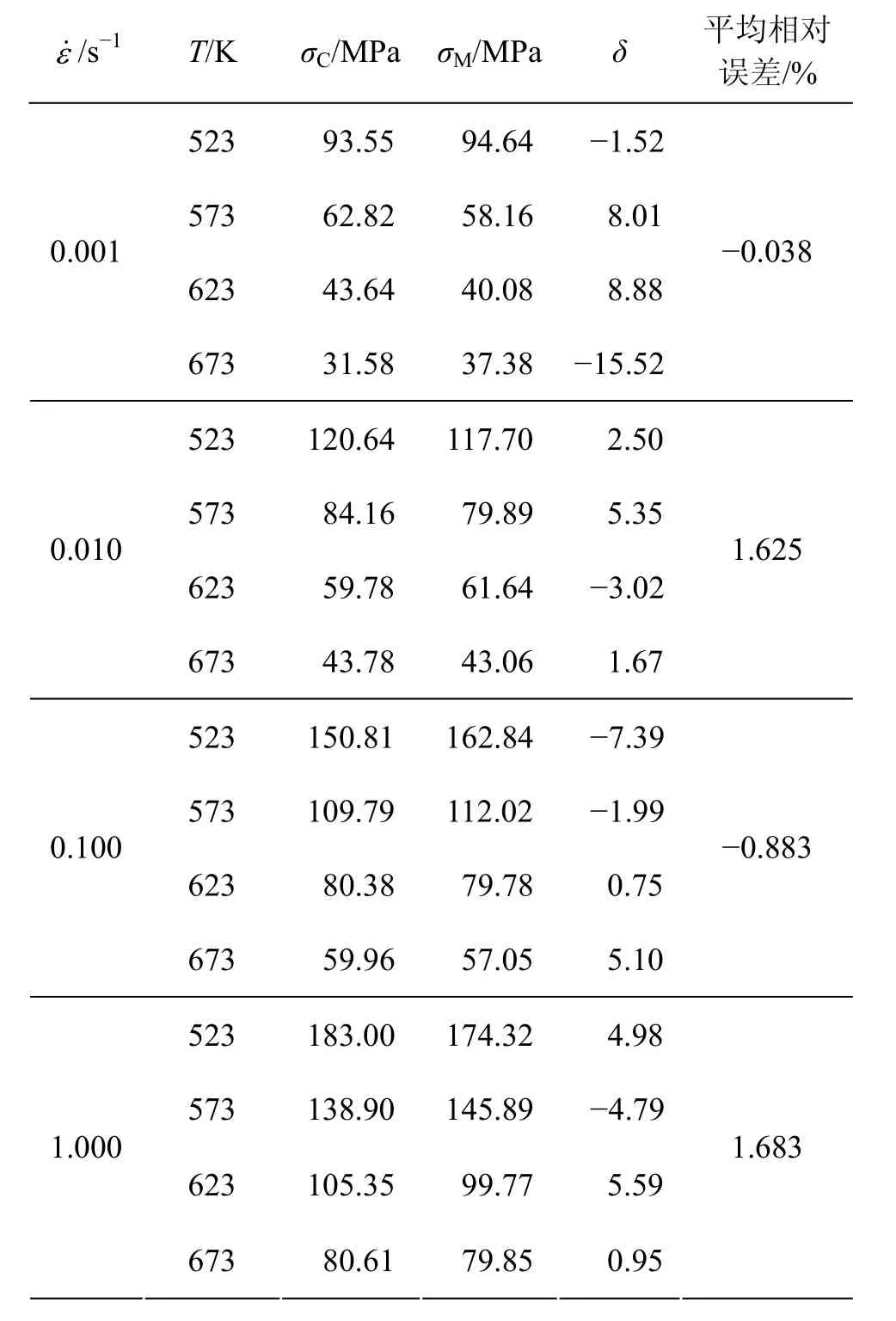
表1 計算峰值應力與實測峰值應力對比Table 1 Comparisons of calculated and measured peak stress

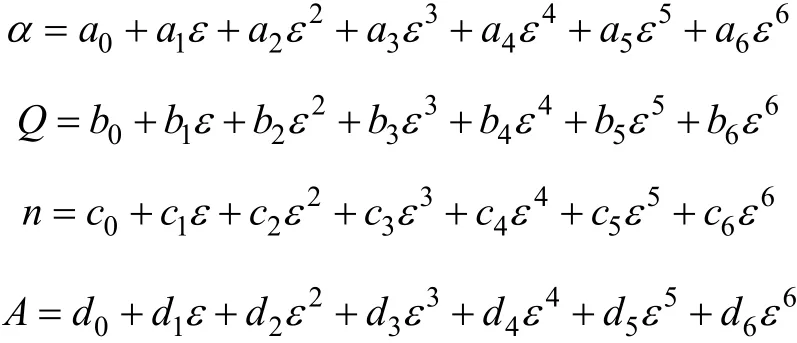
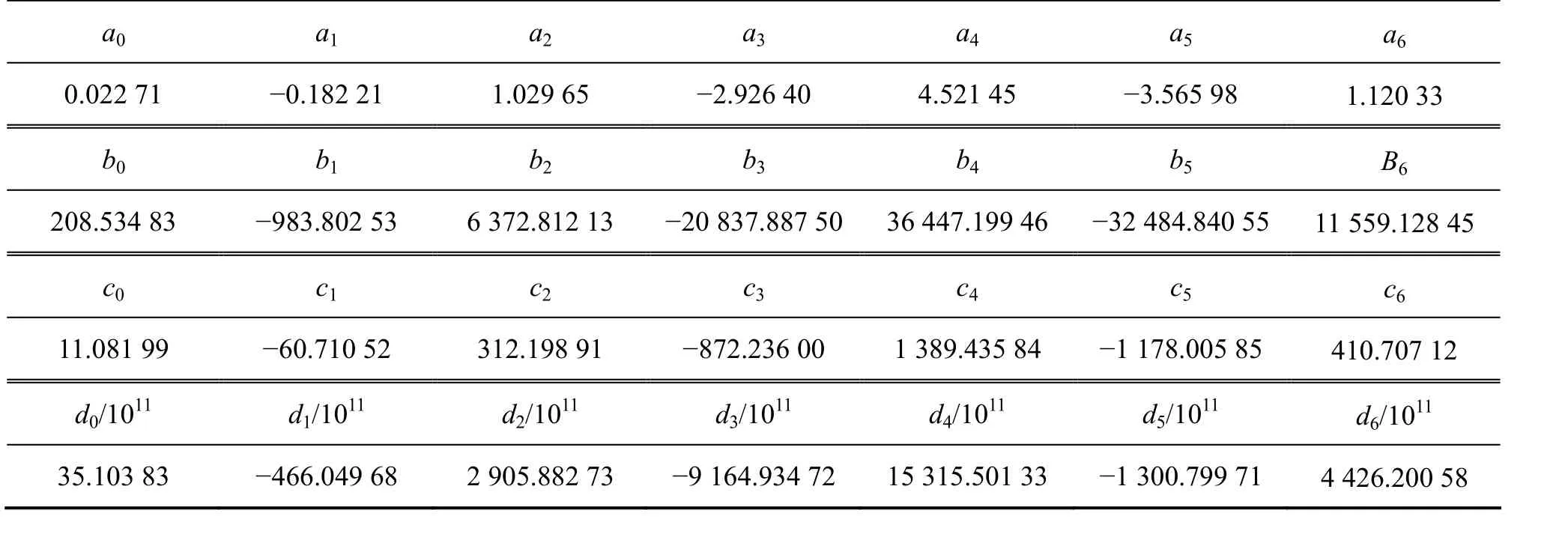
表2 各參數的多項式擬合系數Table 2 Coefficients of polynomial functions

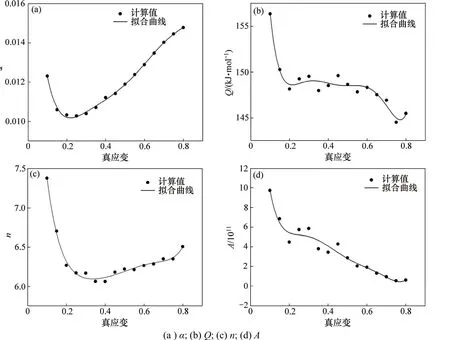
圖6 本構方程中各參數與應變的關系Fig.6 Relationships between coefficients of constitutive equation and strain

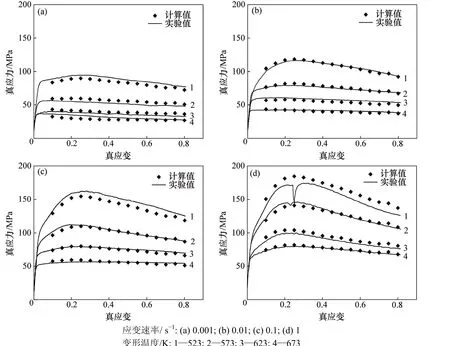
圖7 不同應變速率下實測和計算的真應力-真應變曲線對比Fig.7 Comparisons between calculated and measured stress-strain curves under different strain rates

將引入了應變ε的α，Q，n和A代入式(7)和式(10)即可求得不同應變下的流變應力。圖7所示為采用包含應變的流變應力本構方程計算的流變應力與實測應力-應變曲線的對比圖，從圖 7可以看出：除應變速率為1 s-1、變形溫度為523 K條件下，由于試樣開裂引起應力松弛，導致計算值與實測值偏差較大外，在其他條件下，計算值與實測值都較吻合。

表3給出了應變速率為0.01 s-1時不同應變下，流變應力計算值與實測值的對比。從表3可以看出：不同應變下的平均相對誤差最大值為-3.86%。這表明考慮應變后的改進的本構關系很好地描述了ZK60合金的流變應力。

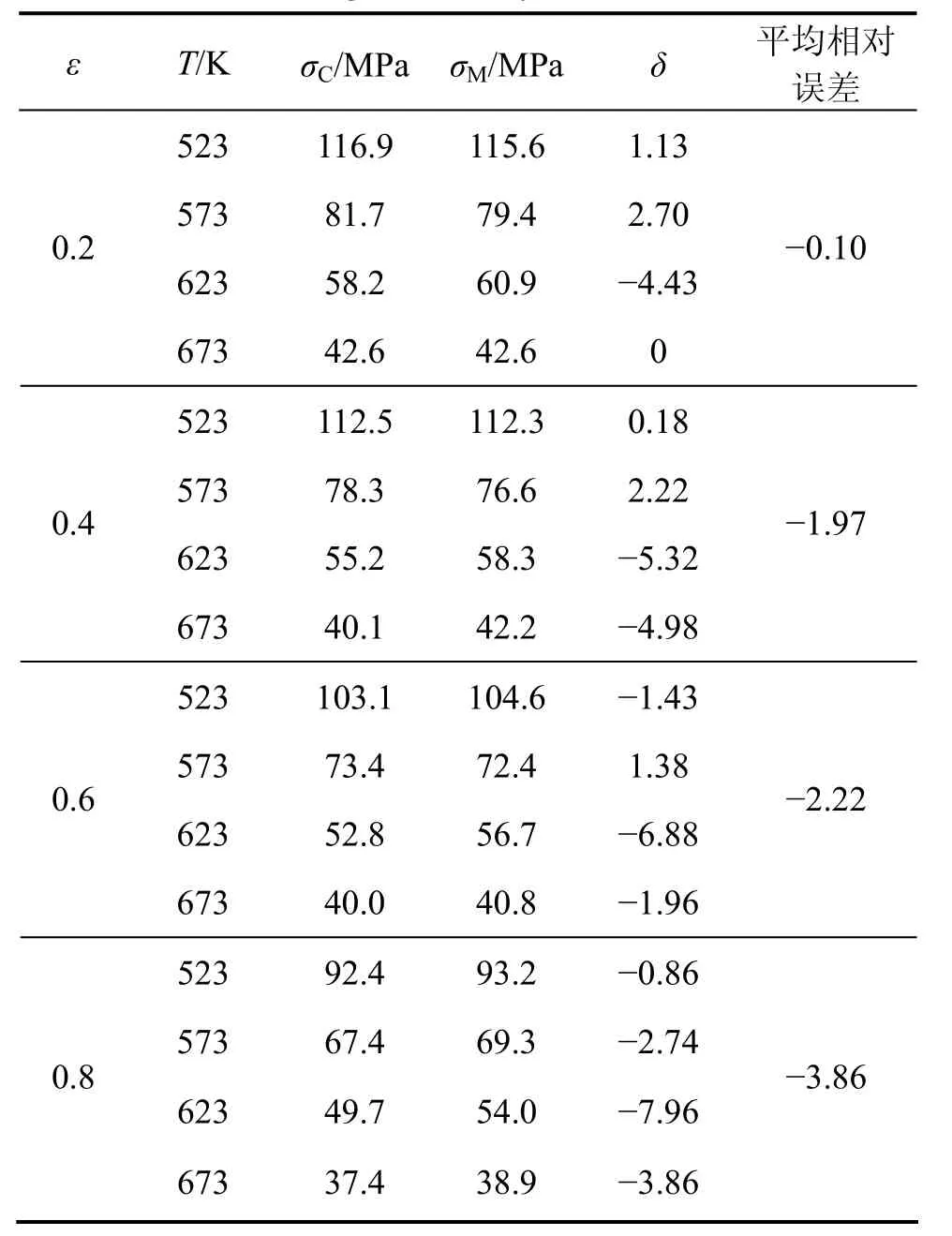
表3 應變速率為0.01 s-1時ZK60鎂合金流變應力實測值σM與計算值σC對比Table 3 Comparisons of measured (σM) and calculated (σC)flow stress of ZK60 magnesium alloy under strain rate of 0.01 s-1

3 結論

(1) ZK60鎂合金高溫壓縮變形真應力-真應變曲線具有動態再結晶特征。當應變速率一定時，流變應力隨著變形溫度的升高而降低；當變形溫度一定時，流變應力隨著應變速率的增加而增大。

(2) 采用雙曲正弦函數修正的Arrhenius關系和Z參數描述了 ZK60鎂合金高溫壓縮變形時的峰值應力，計算結果與實驗結果較符合，最大相對誤差為1.683%。

(3) 考慮應變對流變應力的影響，建立了包含應變的流變應力本構方程，采用該方程計算得到的流變應力曲線與實驗曲線較吻合，最大相對誤差為-3.86%。

[1] 麻彥龍, 潘復生, 左汝林. 高強度變形鎂合金ZK60的研究現狀[J]. 重慶大學學報, 2004, 27(9): 80-85.MA Yan-long, PAN Fu-sheng, ZUO Ru-lin. Review on the research of high-strength wrought magnesium alloys ZK60[J].Journal of Chongqing University, 2004, 27(9): 80-85.

[2] 余琨. 稀土變形鎂合金組織性能及加工工藝研究[D]. 長沙:中南大學材料科學與工程學院, 2002: 89.YU Kun. Study on the microstructure,properties and deformation techniques of rare earth wrought magnesium[D]. Changsha:Central South University. School of Materials Science and Engineering, 2002: 89.

[3] 陳振華, 夏偉軍, 嚴紅革, 等. 鎂合金材料的塑性變形理論及其技術[J]. 化工進展, 2004, 23(2): 127-135.CHEN Zhen-hua, XIA Wei-jun,YAN Hong-ge, et al. Principles and technology of plastic deformation for magnesium alloys[J].Chemical Industry and Engineering Progress, 2004, 23(2):127-135.

[4] 余琨, 黎文獻, 王日初, 等. 變形鎂合金的研究、開發及應用[J]. 中國有色金屬學報, 2003, 13(2): 277-288.YU Kun, LI Wen-xian, WANG Ri-chu, et al.Research,development and application of wrought magnesium alloys[J]. The Chinese Journal of Nonferrous Metals, 2003,13(2): 277-288.

[5] 林啟權, 張輝, 彭大暑, 等. 5182鋁合金熱壓縮變形流變應力[J]. 湘潭大學自然科學版, 2002, 24(3): 84-88.LIN Qi-quan, ZHANG Hui, PENG Da-shu, et al. Flow stress behavior of 5182 aluminum alloy under hot compression deformation[J]. Natural Science Journal of Xiangtan University,2002, 24(3): 84-88.

[6] Galiyev A, Sitdikov O, Kaibyshev R. Deformation behavior and controlling mechanisms for plastic flow of magnesium and magnesium alloy[J]. Materials Transactions, 2003, 44(4):426-435.

[7] McQueen H J. Elevated-temperature deformation at forming rates of 10-2to 102s-1[J]. Metallurgical and Materials Transactions A, 2002, 33(2): 345-362.

[8] Takuda H, Fujimoto H, Hatta N. Modelling on flow stress of Mg-Al-Zn alloys at elevated temperatures[J]. Journal of Materials Processing Technology, 1998, 80/81: 513-516.

[9] Takuda H, Morishita T, Kinoshita T, et al. Modelling of formula for flow stress of a magnesium alloy AZ31 sheet at elevated temperatures[J]. Journal of Materials Processing Technology,2005, 164/165: 1258-1262.

[10] Zhou H T, Zeng X Q, Wang Q D. Flow stress model for AZ61 magnesium alloy[J]. Acta Metallurgica Sinica, 2004, 17(2):155-160.

[11] WANG Ling-yun, FAN Yong-ge, HUANG Guang-jie. Flow stress and softening behavior of wrought magnesium alloy AZ31B at elevated temperature[J]. Transactions of Nonferrous Metals Society of China, 2003, 13(2): 335-338.

[12] Galiyev A, Kaibyshev R, Gottstein G. Correlation of plastic deformation and dynamic recrystallization in magnesium alloy ZK60[J]. Acta Materialia, 2001, 49(7): 1199-1207.

[13] 張婭, 馬春江, 盧晨. 變形鎂合金的塑性變形機制與動態再結晶[J]. 輕合金加工技術, 2003, 31(7): 35-39.ZHANG Ya, MA Chun-jiang, LU Chen. Plastic strain mechanism and dynamic recrystallization of magnesium alloy[J].Light Alloy Fabrication Technology, 2003, 31(7): 35-39.

[14] 陳振華, 許方艷, 傅定發, 等. 鎂合金的動態再結晶[J]. 化工進展, 2006, 25(2): 140-146.CHEN Zhen-hua, XU Fang-yan, FU Ding-fa, et al. Dynamic recrystallization of magnesium alloy[J]. Chemical Industry and Engineering Progress, 2006, 25(2): 140-146.

[15] 陳振華. 變形鎂合金[M]. 北京: 化學工業出版社, 2005:88-98.CHEN Zhen-hua. Wrought magnesium alloy[M]. Beijing:Chemical Industry Press, 2005: 88-98.

[16] Poirier J P. 晶體的高溫塑性變形[M]. 關德林, 譯. 大連: 大連理工大學出版社, 1989: 37-40.Poirier J P. High temperature plastic deformation of crystals[M].GUAN De-lin, trans. Dalian: Dalian University of Science and Technology Press, 1989: 37-40.

[17] 沈鍵. 2091鋁合金高溫塑性變形的研究[D]. 長沙: 中南大學材料科學與工程學院, 1996.SHEN Jian. Study of hot compression deformation of 2091 aluminum alloy[D]. Changsha: Central South University. School of Materials Science and Engineering, 1996.

[18] Jonas J J, Sellars C M, Tegart M W J. Strength and structure under hot-working conditions[J]. International Materials Reviews, 1969, 14(1): 1-24.

[19] 吳文祥, 孫得勤, 曹春艷, 等. 5083鋁合金熱壓縮變形流變應力行為[J]. 中國有色金屬學報, 2007, 17(10): 1667-1671.WU Wen-xiang, SUN De-qing, CAO Chun-yan, et al. Flow stress behavior of aluminum alloy under hot compression deformation[J]. The Chinese Journal of Nonferrous Metals, 2007,17(10): 1667-1671.

[20] Sheppard T, Parson N C, Zaidi M A. Dynamic recrystallization in Al-7Mg[J]. Metal Science Journal, 1983, 17(10): 481-490.

[21] Zener C, Hollomon J H. Effect of strain rate upon plastic flow of steel[J]. Journal of Applied Physics, 1944, 15(1): 22-23.